УРОК ОДНОЙ ЗАДАЧИ Решение стереометрических задач различными методами

УРОК ОДНОЙ ЗАДАЧИ
Решение стереометрических
задач различными методами
Цели:
• Выработать умение рассматривать различные подходы к
решению задач и проанализировать эффект от
применения этих способов решения.
• Выработать умение учащегося выбирать метод решения
задачи в соответствии со своими математическими
предпочтениями, базирующимися на более прочных знаниях
и уверенных навыках.
• Выработать умение составлять план последовательных
этапов для достижения результата.
• Выработать умение обосновать все предпринимаемые
шаги и вычисления.
• Повторить и закрепить различные темы и вопросы
стереометрии и планиметрии, типовые
стереометрические конструкции , связанные с решением
задач.
• Развивать пространственное мышление.
Задачи:
• Анализ различных методов решения задачи.
• Сравнение преимуществ и недостатков
каждого метода.
• Повторение свойств правильной
шестиугольной призмы.
• Подготовка к сдаче ЕГЭ.
• Развитие самостоятельности при
принятии решения.
Задача.
В
правильной
шестиугольной
призме
ABCDEFA1B1C1D1E1F1 сторона основания равна 2,
боковое ребро равно 4. Точка N принадлежит АС,
AN : NC = 1 : 3.
Найти:
1) расстояние от точки В1 до N;
2) расстояние от точки N до прямой C1E1;
3) расстояние от точки N до плоскости B1E1D;
4) расстояние между прямыми B1N и F1D;
5) угол между скрещивающимися прямыми C1N и
FE1;
6) угол между прямой F1N и плоскостью B1E1D;
7) угол между плоскостями A1 N B1 и BEC1 .
1. Расстояние между
двумя точками
Бовиков Бамба
Пыль Юлиана
Дано:
𝐴𝐵𝐶𝐷𝐸𝐹𝐴1 𝐵1 𝐶1 𝐷1 𝐸1 𝐹1
− правильная шестиугольная призма
Ребро основания=2
Боковое ребро=4
N
AC

AN:NC=1:3
Найти:
Расстояние от точки 𝐵1 до N

Метод 1
<ABC= 180·(N-2)/N
=><ABC=120 °
АВ = ВС = 2
По теореме косинусов
𝐴𝐶 2 =𝐴𝐵2 +𝐵𝐶 2 2AB*BC*cos<ABC
АС=2√3 =>AN=2√3*1/4(т.к
AN:NC=1:3)=√3/2
<ВАN=30°,АВ=2,АN=√3/2
𝐵𝑁 2 =4+3/4-√3*√3=7/4
BN=√7/2
𝐵1 𝑁= 𝑁𝐵2 + 𝐵1 𝐵2 =
16 + 7/4 =
71/2
Метод 2
N(-5/4;√3/4;0)
𝐵1 (-1;√3;4)
|𝐵1 𝑁|=
5
4
(1 − )2 +( 3 −
28
16
+ 16=√71/2
3 2
) +(2 +
4
2)2 =
Метод 3
2. Расстояние от точки до прямой
Четырев Василий
Бульдигирова Элла
Дано:
ABCDEFA₁B₁C₁D₁
E₁F₁ - правильная
шестиугольная
призма.
AB = 2
AA₁ = 4
NϵAC, AN:NC=1:3
Найти: расстояние
от N до C₁E₁.
Решение:
Через (·) N проведём прямую, перпендикулярную
AD и BC.
] она пересекает их в точках H и K соответственно.
Тогда ∆ANH и ∆CNB подобны, причём AN:NC=1:3.
] E1C1∩A1D1 = P. ] M ϵ PC1 и MP:PC1=1:3. Очевидно, что
KHǁEC; ECǁE1C1 => KHǁE1C1. Также очевидно, что
KH=PC1, и NH=1/4 BH=1/4 PC1=PM. Итак, NH=PM и
NHǁPM. Значит, NHPM – параллелограмм => HPǁNM.
E1C1
перпендикулярна
(AA1D1)
=>
E1C1
перпендикулярна HP, а т.к. HPǁNM, то E1C1 и NM –
перпендикулярны, т.е. NM – искомое. NM = HP =
.
Найдём координаты точек H и P.
3
AD.
4
] CE∩ AD=T, тогда OT=TD AT=
∆ANH и∆ACT подобны, причем
1
1 3
3
AN:AC=1:4.Тогда AH= 4 ∙AT= 4 ∙ 4 AD= 16 ∙AD.
5
5
5
1
3
HO=AO-AH= 2 ∙AD- ∙AD= 16 ∙AD=16 ∙4= 4 .
16
5
=>H(O; - 4 ; 0).
(·)P (0; 1; 4), тогда
2
337
9
2
HP  0     4 
4
4
1)Рассмотрим ∆C₁D₁E₁:
3
2
2
C₁E₁= C D  sin 120 
1
1
sin 30
0,5
2
3
2)N(- 54 ; 43 ;0); С₁(1; 3 ;4); E₁(1;- 3 ;4).
2
3
91
 5  
2

NC1  1     3 
 4  0 
.

4 
2
 4 
2
2
3
103
 5  
2

NE1  1      3    4  0 
.
4 
2
 4 
2
b
2
Рассмотрим ∆NC₁E₁:
NC₁= 91 ;NE₁= 103 ;C₁E₁=
2
2
;
91
103
2
2

4
a
b

4
2 3
 12  4 3a  a 2
Приравняем правые части:
9
a=
4 3
Подставим значение «a» в
91
2
2
b   a =>
4
b=
337
4
3. Расстояние от точки
до плоскости
Манджиев Павел
Педерова Анжелика
Задача
В правильной шестиугольной призме сторона
основания равна 2, а боковые ребра равны 4,
точка N принадлежит AC, AN:NC=1:3.
Найдите расстояние от точки N до плоскости
В1Е1D.
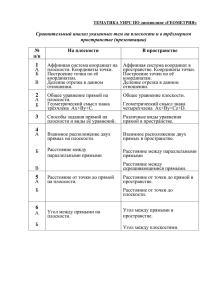
Существуют два
метода решения этой
задачи:
1) Геометрический
2) Координатный
Решить задачу
геометрически
проблемно, так как
сложно определить
куда упадет
перпендикуляр из
точки N на данную
плоскость. Поэтому
решим задачу
координатным
методом.
С1
D1
В1
Е1
А1
F1
C
D
B
N
A
E
F
C1
D1
z
B1
E1
А1
y
F1
x
C
D
B
N
A
E
O
F
Дано:
АВСDEFA1B1C1D1E1F1-правильная
шестиугольная призма.
АВ=2; АА1=4; NϵAC; AN:NC=1:3.
Найти: d(N;B1E1D)
Решение: 1) Введем систему координат как
показано на рисунке.
2)Определим координаты точек :
B1(-1; 3;4)
E1(1;− 3;4)
D(2;0;0)
5
N(− 4 ;
3
;0)
4
3)Пусть уравнение плоскости (B1E1D) имеет вид:
Ax+By+Cz+D=0. Точки B1,E1,D принадлежат данной плоскости. Значит, эти точки
удовлетворяют уравнению плоскости. Составим систему уравнений:
−𝐴 + 3B + 4C + D = 0
A − 3B + 4C + D = 0 
2A + D = 0
3𝐷
+
2
𝐷
−
2
3B + 4C = 0
3B + 4C = 0 
A=−
𝐷
2
𝐷 3
6
𝐷
−4
𝐷
−2
B=−
C=
A=
𝐷
𝐷 3
𝐷
12
x−
𝑦 − 𝑧 + 𝐷 = 0| ∗ −
2
6
4
𝐷
Получим уравнение плоскости :
6𝑥 + 2 3𝑦 + 3𝑧 − 12 + 0
4) Используем формулу нахождения расстояния от точки до плоскости :
|𝐴𝑥0 + 𝐵𝑦0 + 𝐶𝑧0 + 𝐷|
𝑑=
, где
2
2
2
𝐴 +𝐵 +𝐶
𝑥0, 𝑦0,𝑧0 − координаты точки N.
𝐴, 𝐵, 𝐶, 𝐷 − коэфициенты уравнения плоскости
Подставим данные значения в формулу:
5
3
|6 • − 4 + 2 3 • 4 + 0 − 12| | − 18| 6 57
𝑑=
=
=
19
36 + 12 + 9
57
−
Ответ:
6 57
19
4. Расстояние между прямыми
Бабаков Вадим
Сангаева Гиляна
Лиджиева Ольга
Задача.
В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1
найти
расстояние
между B1N и DF1, где N 𝜖 AC, AN/NC = 1/3.
Сторона основания призмы = 2, высота
призмы = 4.
𝑫𝟏
𝑬𝟏
𝑪𝟏
𝐅𝟏
𝑩𝟏
𝑨𝟏
𝐃
𝐂
𝐅
𝑵
𝐁
𝐄
𝑨
𝐁(−𝟏; 𝟑; 𝟎)
𝒚
𝟓 𝟑
𝑵(− ;
; 𝟎)
𝟒 𝟒
𝐀(−𝟐; 𝟎; 𝟎)
𝐅(−𝟏; − 𝟑; 𝟎)
𝐂 (𝟏; 𝟑; 𝟎)
𝐃(𝟐; 𝟎; 𝟎)
𝒙
𝐄(𝟏; − 𝟑; 𝟎)
Метод 1
Каноническое
пространстве
уравнение
прямой
где 𝑥2 - 𝑥1 =𝑎1 , 𝑦2 - 𝑦1 =𝑎2 ,𝑧2 - 𝑧1 =𝑎3 , а
вектор {𝑎1 ; 𝑎2 ; 𝑎3 } – направляющий вектор
этой прямой
в
Метод 1
Тогда расстояние между скрещивающимися
прямыми d:
d=
|(𝐴0 𝐴1 ∗𝑎∗𝑏)|
|𝑎 × 𝑏|
То
есть,
в
числителе
смешанное
произведениетрёх векторов, а в знаменателе
– векторное произведение направляющих
векторов скрещивающихся прямых
Метод 1
Метод 2
𝑖
𝑁𝐵1 x 𝐹1 𝐷= 1/4 3
3
=−6 3 i + 13 j − 2
𝑗
𝑘
3/4 4 =
3
−4
3k
−1/4
𝑁𝐵1 ∗ 𝐹1 𝐷 ∗ 𝐹1 𝑁 = 1/4
3
Тогда искомое d=26 3/17
5 3/4 −4
3 3/4 4 = 26 3
3
−4
Метод 1
Смешанное произведение трёх векторов –
определитель третьего порядка, где в первой
строке матрицы координаты первого вектора
из произведения, во второй – второго, в
третьей – третьего.
Векторное произведение двух векторов –
вектор, координаты которого определяются
определителем третьего порядка, где в первой
строке матрицы единичные векторы i, j, k, во
второй – координаты первого вектора, в
третьей – третьего.
Метод 2
Пусть P(𝑥0 ;𝑦0 ;𝑧0 ), Q(𝑥1 ;𝑦1 ;𝑧1 ). P лежит на 𝐵1 𝑁,
Q – на 𝐹1 𝐷 . Вектор PM перпендикулярен
𝐵1 𝑁 и 𝐹1 𝐷 , то есть его длина – искомое
расстояние между прямыми. Выражаем
вектор PM через 𝐵1 𝑁и 𝐹1 𝐷, его произведения
к двум векторам скрещивающихся прямых
равны 0. Откуда можно найти его длину
Метод 2
𝑫𝟏
𝑬𝟏
𝑪𝟏
𝐅𝟏
𝑩𝟏
𝐐
𝐃
𝑨𝟏
𝐏
𝐂
𝐅
𝑵
𝐁
𝐄
𝑨
Метод 2
• 𝐵1 𝑃 =
𝜆
5 3
− ;−
𝜆; −4
4
4
; 𝐹1 𝑄 =
3𝜁; 3𝜁; −4𝜁 ;
•
𝜆 3 4
P(-1- ;- 𝜆
4 4
+ 3; −4𝜆 + 4);Q(3𝜁 − 1; 3𝜁 −
3; 4 − 4𝜁)
•
𝑃𝑄 ∗ 𝐹1 𝐴 = 0
𝑃𝑄 ∗ 𝐵1 𝑁 = 0
Метод 2
Этот метод крайне нерационален, потому что
приходится выражать вектор PM через 2
переменные, после чего находить эти
переменные.
Метод 3
Через одну из скрещивающихся прямых
можно провести плоскость, параллельную
второй. Построим плоскость, параллельную
𝑁𝐵1 через 𝐹1 𝐷. Для этого проведём из точки
𝐷 отрезок 𝐷Q, равный и параллельный𝑁𝐵1 .
Метод 3
𝑸
𝑫𝟏
𝑬𝟏
𝑪𝟏
𝐅𝟏
𝑩𝟏
𝑨𝟏
𝐃
𝐂
𝐅
𝑵
𝐁
𝐄
𝑨
Метод 3
Плоскость𝐷𝑄𝐸1 параллельна прямой 𝑁𝐵1 . То
есть
нахождение
расстояния
между
скрещивающимися прямыми свелось к
нахождению
расстояния
между
параллельными прямой и плоскостью.
Используя уравнение плоскости 𝐷𝑄𝐸1 и
координаты точки 𝐵1 , находим это
расстояние по формуле
d=
|𝐴∗𝑥0 +𝐵∗𝑦0 +𝐶∗𝑧0 |
𝐴2 +𝐵2 +𝐶 2
.
Метод 3
Уравнение плоскости (𝑄𝐷𝐹1 ):
21𝑥 − 13 3𝑦 + 6𝑧 + 36 = 0
То есть расстояние d =
27
246
5. Угол между скрещивающимися
прямыми
Болаева Альмина
Семенов Галсан
Мусова Виктория
Задача:
В правильной шестиугольной призме
ABCDEFA1B1C1D1 E1F1 сторона основания
равна 2, боковое ребро 4. Точка N
принадлежит ребру AC так, что AN:NC =
1:3. Найти угол между прямыми C1N и FE1.
Введём призму в декартовую систему координат с
центром в точке О
ВИД СВЕРХУ:
1)
=>
=>
2)
3)
=>
Решение:
М
6. Угол между прямой и
плоскостью
Бюрчиев Эренцен
Первенов Эдуард
Сухурова Виктория
Задача.
• Вправильной шестиугольной призме
ABCDEF𝐴1 𝐵1 𝐶1 𝐷1 𝐸1 𝐹1 сторона основания
равна 2, а боковые рёбра – 4. N
принадлежит AC, AN:NC=1:3. Найти угол
между прямой 𝐹1 N и плоскостью (𝐵1 𝐸1 𝐷).
Метод 1
• 𝐵1 (1; 3;4), 𝐸1 (1; − 3;4); D(2;0;0)
Составим уравнение плоскости:
2 3x+2y+ 3z-4 3=0;
• Пусть 𝑛 - нормаль-вектор к (𝐵1 𝐸1 D), тогда
𝑛={2 3;2; 3}
• Построим прямую𝐸1 𝑁1 , параллельную
стороне𝐹1 N, тогда координаты 𝑁1 (1;- 3;4)
n  19
83
E1 N1 
2
n  E1 N1
2 3
2 3
COS 

 SIN    ARCSIN
1577
1577
n  E1 N1
Метод 2
• Достроим сечение (𝐵1 𝐸1 D) до
параллелограмма 𝐵1 𝐸1 DK. Точка
𝐸1 сечению, следовательно нужно найти
основание перпендикуляра на плоскость.
Но этот метод нерационален, поэтому его
лучше не использовать.