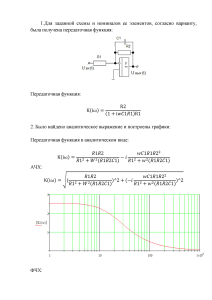
МИХАЙЛОВСКАЯ ВОЕННАЯ АРТИЛЛЕРИЙСКАЯ АКАДЕМИЯ 5 кафедра боевого применения подразделений артиллерийской разведки Тема № 2 Занятие № 9 АНАЛИЗ УСТРОЙСТВ И СИСТЕМ РАДИОАВТОМАТИКИ Автор: КТН, доцент Рудианов Г.В. Санкт-Петербург 2019 МИХАЙЛОВСКАЯ ВОЕННАЯ АРТИЛЛЕРИЙСКАЯ АКАДЕМИЯ 5 кафедра боевого применения подразделений артиллерийской разведки УТВЕРЖДАЮ Начальник 5 кафедры полковник М.Сафронов « 22 » июля 2019 г. Разрешаю использование в 20__-20__ учебном году Начальник 5 кафедры полковник М.Сафронов «___» __________ 20__ г. Кандидат технических наук, доцент Рудианов Г.В. ЧАСТОТНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ АВТОМАТИЧЕСКИХ СИСТЕМ Текст лекции (Тема № 2, занятие № 9) Обсуждено и одобрено на заседании предметно-методической комиссии « 21 » мая 2019 г., протокол № 10 Санкт-Петербург 2019 2 Текст лекции Учебные и воспитательные цели: 1. Изучить методику составления дифференциальных уравнений автоматической системы. 2. Изучить методику составления уравнения автоматической системы в изображениях Лапласа. 3. Воспитывать у курсантов общую инженерную культуру и гордость за достижения отечественной науки и техники. 1. ЧАСТОТНАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ [1] с. 32 Если на вход линейного звена или системы звеньев подать гармонический сигнал, то на выходе после окончания переходного процесса также будет гармонический сигнал. Причем частота выходного сигнала будет равна частоте входного. Амплитуда и сдвиг фаз выходного процесса изменяются по сравнению с входным. Частотными характеристиками системы называются зависимости изменения частоты и фазы колебаний на выходе системы в зависимости от частоты гармонических входных колебаний. Существуют следующие виды частотных характеристик: амплитудно-частотная характеристика (АЧХ); фазо-частотная характеристика (ФЧХ); амплитудно-фазочастотная характеристика (АФЧХ). АЧХ звена (системы) – отношение амплитуды выходного гармонического сигнала к амплитуде входного в функции его частоты w в установившемся режиме. ФЧХ звена (системы) называется разность фаз между выходным и входным сигналами в установившемся режиме. АФЧХ – это годограф радиус-вектора, длина которого – АЧХ, а угол поворота – ФЧХ. Пусть дано дифференциальное уравнение динамической системы: (N) (M ) (1) aN x2 aN 1 x2 aN 2 x2 ... a0 x2 bM x1 bM 1 x1 bM 2 x1 ...b0 x1 Рассмотрим установившуюся реакцию этой системы на гармоническое входное воздействие, которое запишем в комплексной форме: x1 (t ) x1m e j ( t ) x1m e jt (2) где х1m – амплитуда гармонических колебаний; ω – круговая частота колебаний; ψ1 – начальная фаза колебаний; x1m x1m e j – комплексная амплитуда колебаний. 1 1 Будем искать частное решение неоднородного уравнения (1) при нулевых начальных условиях в виде x2 (t ) x2 m e j ( t ) x2 m e jt (3) Подставляя (2) и (3) в (1) и учитывая, что 2 d k j ( t ) e (t ) k e jt k dt (4) Получим aN x2 m ( j)0 aN 1 x2 m ( j)1 aN 2 x2 m ( j)2 ... a0 x2 m ( j) N bM x1m ( j)0 bM 1 x1m ( j)1 bM 2 x1m ( j)2 ... b0 x1Mm ( j) M (5) 3 Вынося x2m и x1m за скобки, получим: x2 m a N a N 1 j a N 2 ( jω) 2 ... a0 ( jω) N (6) x1m bM bM 1 jω bM 2 ( jω) 2 ... b0 ( jω) M . Деля x2m на x1m , получаем частотную передаточную функцию динамической системы, описываемой дифференциальным уравнением (1). b b j b2 ( j) 2 ... bM ( j) M (7) K ( j) 0 1 a0 a1 j a2 ( j) 2 ... a N ( j) N Частотная передаточная функция может быть формально получена из передаточной функции путем подстановки p = jω. Частотная передаточная функция есть комплексная функция переменной ω и, как всякая комплексная функция, может быть представлена в одной из форм: (8) K ( j) U () jV () или K ( j) K ( j) e j ( ) . где U(ω) − вещественная часть функции K(jω); V(ω) − мнимая часть функции K(jω); A(ω) − модуль функции K(jω); ψ(ω) − аргумент функции K(jω) или фаза. Модуль частотной передаточной функции динамической системы определяет амплитудно-частотную характеристику (АЧХ) этой системы, а аргумент – фазо-частотную характеристику (ФЧХ). Частотная передаточная функция является вектор-функцией и графически изображается на комплексной плоскости в виде вектора с прямоугольными координатами U(ω) и V(ω) или с полярными координатами А(ω) и ψ(ω) (рис. 1). 2 jV +∞ ω 1 0 Im( W( ω) ) U(ω) 2 1 0 V(ω) 1 A(ω ) ψ(ω) 1 U 0 W(jω) ω −∞ Рис. 1. Частотная передаточная функция 2 При изменении переменной ω в пределах (−∞, +∞) конец вектора описывает криRe( W( ω) ) вую, которую называют амплитудно-фазовой характеристикой системы (АФХ). Амплитуда х2m выходных колебаний системы при неизменной амплитуде входных зависит от частоты этих колебаний. Отношение амплитуды выходных колебаний к амплитуде входных, как функция частоты, определяется модулем частотной передаточной функции системы А(ω). Фазовый сдвиг ∆ψ между выходными и входными колебаниями 4 также зависит от частоты этих колебаний и, как функция частоты, определяется аргументом частотной передаточной функции системы ψ(ω). Таким образом, частотная передаточная функция динамической системы полностью определяет прохождение гармонического колебания через эту систему. П р и м е р 1. Дано уравнение системы Tx2 x2 kx1 и входное воздействие x1 (t ) x1 m sin t . Найти установившееся движение системы, используя частотную передаточную функцию. Р е ш е н и е . Подстановкой p = jω находим Tjx2 x2 kx1 . Выражаем передаточную функцию k . K ( j) 1 jT Комплексное число в знаменателе выражаем в показательном виде: 1 jωT 1 ω2T 2 е j arctgTω . Тогда k K ( j) е j arctgT . 2 2 1 T Для входного воздействия x1 (t ) xm sin t , полагая ω=Ω, получим А() k 1 T 2 2 ψ() arctg Т , отсюда x 2 y (t ) x1m А() sin( t ψ()) x1m k 1 T 22 sin( t arctg Т ) . Таким образом, установившийся процесс на выходе линейной системы при гармоническом входном воздействии наиболее просто определить при использовании ее частотной передаточной функции. [2] с. 55 Рассмотрим построение АФХ на примере колебательного звена. В выражении передаточной функции колебательного звена при коэффициенте усиления 1 1 K ( p) 2 2 T p 2Tp 1 положим p=jω и, принимая во внимание, что j2 = – 1, получим 1 K ( j) . 2 2 (1 T ) j 2T Для построения АФХ необходимо данное выражение представить в алгебраическом виде: K ( j) U () jV () , где U(ω) – вещественная часть; V(ω) – мнимая часть, т.е. отделить вещественную часть от мнимой. Для этого необходимо умножить числитель и знаменатель последнего уравнения на выражение, сопряженное знаменателю, и отделить вещественную часть от мнимой. 5 Правило деления комплексных чисел выглядит следующим образом: a1 jb1 a1a2 b1b2 a b ab 2 j 2 21 12 2 . 2 a2 jb2 a2 b2 a2 b2 Таким образом, передаточная функция колебательного звена (1 T 2 2 ) 2T K ( j) j . 2 2 2 2 2 2 2 (1 T ) (2T ) (1 T ) (2T ) 2 Модуль и фаза АФХ А() [U ()]2 [V ()]2 , V () . () arctg U () Таким образом, для колебательного звена получаем: (1 T 2 2 ) 2 (2T ) 2 1 . А( j) 2 2 2 2 2 2 2 (1 T ) (2T ) (1 T ) (2T ) 2 2T () arctg . 1 T 22 Построенная по данному уравнению АФХ колебательного звена приведена на рис. 2. Q(ω) 1 +∞ ω 0 0.5 P( ω) k ω=±∞ 0.5 φ1 0 0.5 1 ω2 ω=0 0.5 1 P(ω) K(jω 1) ω1 0 ω −∞ Рис. 2. АФХ колебательного звена Q( ω) 2. ПЕРЕХОДНАЯ И ВЕСОВАЯ ФУНКЦИЯ [1] с. 25 Переходная функция служит для оценки качества работы автоматической системы в переходном режиме. Переходной функцией линейной динамической системы называют отклик этой системы на единичную ступенчатую функцию, определяемую как 0 при t 0, 1(t ) . 1 при t 0. При заданном дифференциальном уравнении линейной динамической системы ее переходная функция q(t) определяется: q(t ) K ( p)1(t ) . 6 Перейдем в область изображений по Лапласу: Q( р) K ( p)1( p) , где 1( p) L1(t ) 1/ p . Откуда, используя таблицы преобразования Лапласа и снова переходя во временную область, получим 1 q(t ) L1 K ( p)1(t ) . p f(t) 1 (t ) 2 1(t) 3 t 4 1 t n 1 (n 1)! 5 e t Таблицы преобразования Лапласа F(p) f(t) 1 1 p 1 p2 1 pn 1 p 6 te t 7 sin t 8 cos t 9 e t sin t 10 e t cos t F(p) 1 ( p ) 2 2 p 2 p 2 p 2 ( p ) 2 2 p ( p ) 2 2 Необходимость умножения на 1(t) функции, полученной в результате обратного преобразования Лапласа, обусловлена тем, что переходная функция как реакция на воздействие, отличное от нуля лишь при t ≥ 0, равна нулю при t < 0, т.е. q(t) = 0 при t < 0, что и обеспечивается введением множителя 1(t). Графическое изображение переходной функции называют переходной характеристикой. Типовые переходные характеристики автоматических систем приведены на рис. 3. Рис. 3. Типовые переходные характеристики автоматических систем Кривые на рис. 3, а, б соответствуют устойчивой системе, кривые на рис. 3, в, г – неустойчивой. 7 П р и м е р 2 . Задана система, описываемая уравнением (Tp 1) y kx , где х – вход; y – выход. Определить переходную функцию системы. Р е ш е н и е . Передаточная функция k , K ( p) Tp 1 Переходная функция системы k , Q( p) K ( p) 1( p) p(Tp 1) Для нахождения оригинала переходной функции с использованием таблиц Лапласа разложим данное выражение на элементарные дроби. Используем метод неопределенных коэффициентов: 1 А В А АTp Вр . p(Tp 1) p (Tp 1) р(Tp 1) Определим р, при которых знаменатель обращается в ноль: р1 = 0 и р2 = –1/Т. Подставляя эти значения в числитель и приравнивая его к единице, определяем коэффициенты: А = 1, В = –Т. Таким образом, переходная функция системы 1 T . Q( p) k p Tp 1 T 1 Табличная функция соответствует оригиналу 1(t), а функция , преобразоp Tp 1 1 ванная к табличному виду , соответствует оригиналу e t / T . p Тогда q(t ) L1 [Q( p)] k 1(t ) e t / T 1(t ) k (1 e t / T )1(t ) . [1] с. 28. Весовой функцией линейной системы называют отклик этой системы на единичную дельта-функцию, которая может быть определена как производная единичной ступенчатой функции: 0 при t 0, d (t ) 1(t ) dt при t 0. Эту функцию иногда называют функцией веса. Весовая функция линейной системы равна: w(t ) K ( p)(t ) K ( p) p 1(t ) . Учитывая, что q(t ) K ( p)1(t ) – оригинал переходной функции, получаем: d w(t ) q(t ) p q (t ) . dt Таким образом, функция веса динамической системы равна производной переходной функции этой системы. Весовую функцию можно также выразить следующим образом. w(t ) K ( p)(t ) . Поскольку изображение дельта-функции δ(t) равно единице, то W ( р) K ( p) . 8 Таким образом, функция веса системы равна передаточной функции системы. П р и м е р 3 . Задана система, описываемая уравнением Ty (t ) y (t ) kx(t ) . Определить весовую функцию данной системы. Р е ш е н и е . Записываем уравнение система в операционном виде и определяем ее передаточную функцию k . K ( p) TY ( p) p Y ( p) kX ( p) ; Tp 1 Определяем весовую функцию w(t ) L1[ K ( p)] . Приводим данное выражение к табличному виду: k k 1 K ( p) . Tp 1 T p 1 T Таким образом k t w(t ) e T . T Литература 1. В.А. Бесекерский и др. Радиоавтоматика. Учебн. пособие для студ. вузов спец. «Радиотехника» –М.: Высш. школа. 1985. 2. Михайлов. Теория управления Разработал доцент, кандидат технических наук Г.Рудианов 9