Наибольшее и наименьшее значение функции, непрерывной на

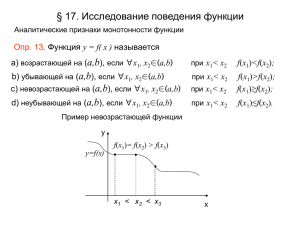
Наибольшее и наименьшее
значение функции, непрерывной
на отрезке
f ( x ) : [ a, b]  R
m  min f (x)
x[ a ,b ]
M  max f (x)
x[ a ,b ]
f ( x )  C[ a , b ]
 x0 , x1  [a, b]
2-я теорема Вейерштрасса
m  f ( x1 )
M  f ( x0 )
max f (x)  M  f ( x0 )
x[ a ,b ]
x 0  [ a, b ]
a  x 0 b
x0  a?
f max ?
f (a)
x0  b
f (b)
  0
(
f (x )
?

? f (x)
f ( x0 )  M 
x0  
x0
x0  
M 
)
f
f ( x0 ) ? max
M  f (b)
y
f (b)
y  f (x)
m  f ( x0 )
x0
0
a
f ( x0 )
b
x
Правило нахождения наибольшего и
наименьшего значения
1)
x1 ,...xn
2)
f ( x1 ),... f ( xn ), f (a), f (b)
3)
- критические точки на
( a, b)
m  ?min  f ( x1 ),... f ( xn ), f (a), f (b)
M ?max  f ( x1 ),... f ( xn ), f (a), f (b)
Пример.
a
x
Коробка наибольшей вместимости
v(x)  x(a  2 x) 2
?
a
0 x
2
?
Пример.
Коробка наибольшей вместимости
?
a
x
v(x)  x(a  2 x) 2
1)
критические точки
v (x) 
0 x
?
?
(a  2 x) 2  4 x(a  2 x)  (a  2 x)( a  6 x)
?
(a  2 x)( a  6 x)
x1 
?
a
2
a
2
a
(0, )
2
0
x2 
?
a
6
a
(0, )
2
Пример.
Коробка наибольшей вместимости
?
a
x
v(x)  x(a  2 x) 2
1)
0 x
a
2
a
6
критическая точка на
x1 
v (x)  (a  2 x)( a  6 x)
a
(0, )
2
 2(a  6 x)  6(a  2 x)
v (x)  ?
a
v ( ) 
6
?
? 0
x1 
?
v(x)
a
6
a
a
 2( a  6 )  6 ( a  2 )
6
6
точка максимума для
Пример.
Коробка наибольшей вместимости
?
x
v(x)  x(a  2 x) 2
1)
2)
x1 
a
6
0 x
a
2
точка максимума
3
a
a 2 2
2a
(
a
)

v( ) 
6 3
27
6
?
v(0)  0?
?
a
v( ) ?0
2
a
Пример.
Коробка наибольшей вместимости
?
a
x
v(x)  x(a  2 x) 2
1)
x1 
2)
a
v( ) 
6
3)
a
6
0 x
a
2
точка максимума
2a 3
27
a
v(0)  v( )  0
2
vmax ?
 2a 3

max  ,0,0 
 27

a
x
6
2a 3
27
?
Направление выпуклости и точки
перегиба кривой
Выпуклость кривой в точке M 0 направлена вниз
  0 x  ( x0   , x0 )  ( x0 , x0   )
f (x)

f ( x0 )  f ( x0 )( x  x0 )
y  f (x)
y
M0


0
x0  
x 0 x0  

f ' ( x0 )
касательная
x
Выпуклость кривой в точке M 0 направлена вверх
  0 x  ( x0   , x0 )  ( x0 , x0   )
f (x)

f ( x0 )  f ( x0 )( x  x0 )
M0
y

касательная

y  f (x)
0
x0  
x 0 x0  
x
y  f (x)

выпуклость, направленная
вверх (вниз) на
( a, b)
f ' ( x)

x  ( a, b)
график функции лежит
не выше (не ниже)
любой своей касательной
M0
y  f (x)
точка перегиба кривой
 ( x0   , x0   )
выпуклость кривой
меняется при переходе через
y
x0
вниз
M0
y  f (x)
вверх
0
x0  
x 0 x0  
x
выпуклость
вниз
y
? Y

y Y
вверх
?
0
sign
y  Y y  Y  0
y Y
y
y  f (x)

M0


y
Y
0
x0
x
x
y Y
?0
 f ( x0 )  f ( x0 )( x  x0 )
касательная
?
y  Y ? f ( x)  [ f ( x )  f ' ( x )( x  x )]
Y
0
0
0
f ( x0 )
f [ x0   ( x  x0 )]
2
f
(
x
)

(
x

x
)

(
x

x
)
f (x) 
0
0
0
1!
2!
?
0  1
y  Y ?
f [ x0   ( x  x0 )]
( x  x0 ) 2
2
формула Тейлора
f ( x0 )
непрерывна в
x0
y Y
?0
f [ x0   ( x  x0 )]
( x  x0 ) 2
2
y Y 
f ( x0 )
0
sign f ( x ) ? sign f [ x
0
0
0
0  1
0
  ( x  x0 )]
0
0
устойчивость знака непрерывной функции
y Y
y Y 
?0
f [ x0   ( x  x0 )]
( x  x0 ) 2
2
f ( x0 )
sign
y Y ?
 sign
f ( x0 )
0
0
f ( x0 )
 sign f [ x

0
  ( x  x0 )]
y  Y ? 0 x  x0
выпуклость вниз


0  1
M 0 ( x0 , f ( x0 ))
y Y
sign
f ( x0 )
f ( x0 )
0
выпуклость вниз
?0
 sign y  Y
 y  Y 0


f ( x0 )
0
выпуклость вверх
M 0 ( x0 , f ( x0 ))
 y  Y ? 0
M 0 ( x0 , f ( x0 ))


Теорема 8 (необходимое условие точки перегиба).
M 0 ( x0 , f ( x0 ))
точка перегиба кривой
y  f (x)

f ( x0 )  0

M 0 ( x0 , f ( x0 ))
точка перегиба кривой
y  f (x)
нет

?
O(0,0)
y
f ( x0 )  0  
да
f ( x)  x
f (x)  4x
yx
4
?
f (x)  12x
? 0
3
2
4
f (0)
0
x 0
O
x
x0
Теорема 9 (достаточный признак точки перегиба).
y  f (x)
 f (x)
непрерывная в точке
x0
x  U ( x0 )
f ( x0 )  0
f (x) меняет знак
при переходе через
f (x)
(
x0  

x
0


M 0 ( x0 , f ( x0 ))
точка перегиба кривой
y  f (x)

x0

)
x0  
Доказательство:
y  f (x)
f ( x0 )  0
  0
f (x)
(
x0  


sign
sign f (x)


)
x
x 


f (x )
0
M 0 ( x0 , f ( x0 ))
0
точка перегиба
Задача.
f ( x0 )
0
y  f (x)
f ( x0 )
0
M 0 ( x0 , f ( x0 ))
точка перегиба
  0
f (x)
(
x0  

f ( x0 )
0
f (x)


x0
?
U ( , x0 )

)
x0  
y  f (x)
M 0 ( x0 , f ( x0 ))
Oy
касательная
f (x) 

 f ( x0 )
f ( x)  x
2
1 3
x
3
?
2 1

f (x)  ?
9 x
3
5
f (x)  0
x 
?
x0
 f (0)

1
3
y  f (x)
M 0 ( x0 , f ( x0 ))
касательная
f (x) 
2 1

9 3 x5
O(0,0)
Oy

x0
точка перегиба
?
f (x)

 f ( x0 )
f (0)

f ( x)  x

 

1
3
Достаточный признак точки перегиба
y  f (x)
 f (x)
касательная в

x  U ( x0 )
f ( x0 )  0
непрерывная в

f (x) меняет знак
при переходе через
M 0 ( x0 , f ( x0 ))
x0
может быть

U ( x0 )
M 0 ( x0 , f ( x0 ))

точка перегиба кривой
y  f (x)
Oy