. Исследование поведения функции § 17 a,b Опр. 13.
advertisement
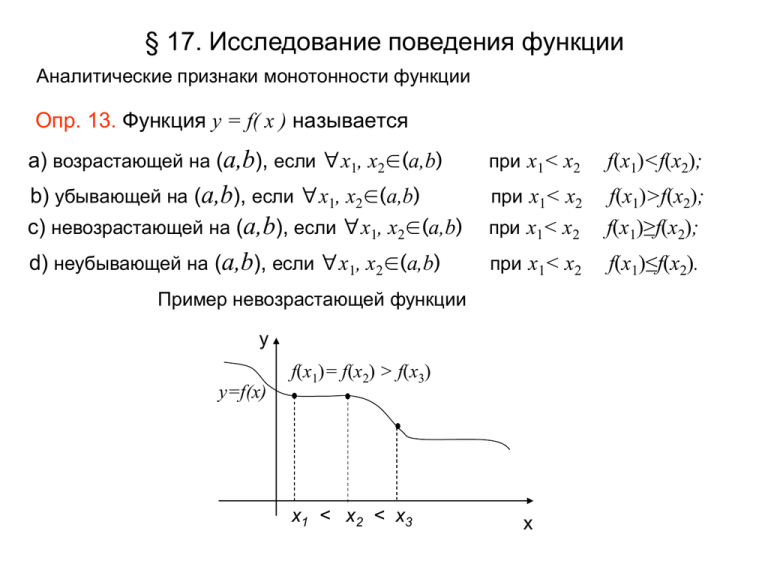
§ 17. Исследование поведения функции Аналитические признаки монотонности функции Опр. 13. Функция y = f( x ) называется а) возрастающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)<f(x2); b) убывающей на (a,b), если ∀x1, x2∈(a,b) c) невозрастающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 при x1< x2 f(x1)>f(x2); f(x1)≥f(x2); d) неубывающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)≤f(x2). Пример невозрастающей функции y y=f(x) f(x1)= f(x2) > f(x3) x1 < x2 < x3 x Теорема 17.1. (Достаточное условие строгой монотонности) Пусть y=f(x) непрерывна на [a,b] и дифференцируема на (a,b), тогда если а) f '(x) >0 на (a,b), то f(x) возрастает на (a,b); b) f '(x) <0 на (a,b), то f(x) убывает на (a,b). Теорема ЛАГРАНЖА Замечание. Обратное утверждение (необходимость) не верно. Пусть функцияфункция y=f(x) может быть возрастающей на (a,b) , Контр пример: а производнаяи удовлетворяет нестрогому f '(x) ≥0 . а)ее определена непрерывна на отрезке [неравенству a,b] Пример б) дифференцируема 3 y=x y '=3x2 y‘(0)=0 на интервале (a,b). y что Тогда найдется хотя бы одна точка С∈(a,b), такая, y=x3 f (C ) f (b) f (a ) ba x Опр. 14 . Говорят, что f '(x) меняет знак в точке x0 , если существует окрестность точки x0: (x0 - δ, x0 + δ), в которой при x < x0 f '(x) сохраняет один знак, а при x > x0 – противоположный. Опр. 16. Точки, в которых f критическими точками. '(x) =0 или не существует, называются Возможные варианты критических точек y экстр. x0 f '(x) y f '(x)=0 нет экстр. x0 x экстр. x0 нет экстр. x0 f '(x) y x экстр. x0 нет экстр. x0 x Теорема 17.2. (1ый достаточный признак экстремума) Пусть y = f (x) непрерывна и дифференцируема в (a,b), x0 – критическая т., тогда а) если при переходе слева направо через x0 f с «+» на «-», то в т. x0 f (x) имеет максимум; '(x) b) если знак производной меняется с «-» на «+», то в минимум. x0 x0∈(a,b) меняет знак f(x) имеет Теорема 17.3. (2ой достаточный признак экстремума) Если в критической точке x0 функции y = f(x) обращается в ноль не только первая производная но и все последующие до (n - 1) - ой включительно, т.е. f '(x0)= f '' (x0)= f ''' (x0)=…= f (n-1)(x0)=0, а f (n)(x0)≠0, тогда x0 будет точкой экстремума, если n – четное; x0 не будет точкой экстремума, если n – нечетное. Характер экстремума определяется знаком f (n)(x0)≠0. При f (n)(x0) < 0 - в x0 максимум, при f (n)(x0 ) > 0 - в x0 минимум. Отыскание наибольшего и наименьшего значения функции на [a, b] Вспомним: b] выполняется неравенство f ( x ) ≤ f ( x0 ), то говорят, функция y = f ( x ) имеет в точке x0 глобальный максимум Если ∀ x ∈ [a, b] f ( x ) ≥ f ( x0 ), то в точке x0 глобальный минимум Если ∀ x ∈ [a, План 1. Найти критические точки xi 2. Вычислить 3. Сравнить. ( f ' (xi)=0 ) f ( xi ), f ( a ), f ( b ) Выпуклость, вогнутость, точки перегиба y Опр 17. Кривая обращена выпуклостью вверх на (a,b), если все точки кривой лежат ниже любой ее касательной на (a,b). Кривая называется выпуклой. Опр 18. Кривая обращена выпуклостью вниз на (a,b), если все точки кривой лежат выше любой ее касательной на этом интервале. Кривая называется вогнутой. a x b x a x b x y Теорема 17.4. (Достаточное условие выпуклости и вогнутости кривой) Пусть y = f (x) непрерывна на [a,b], и имеет в (a, второго порядка включительно, тогда b) производную до а) если во всех точках интервала (a, b) вторая производная функции отрицательна f '' (x) < 0, то кривая на (a, b) выпукла; b) если во всех точках интервала вторая производная положительна f '' (x) > 0, то кривая на (a, b) вогнута. f (x) Опр 19. Точка (x0;y0), лежащая на кривой f(x) называется точкой перегиба функции y=f(x), если существует окрестность точки x0 такая, что при x< x0 кривая лежит по одну сторону касательной, при x > x0 - по другую сторону касательной. y Следствие из достаточного условия выпуклости и вогнутости кривой. (Необходимое условие точки перегиба) Если вторая производная в некоторой точке x0 равна нулю или не существует f ''(x0 )=0 или f ''(x0) ∃, то эта точка есть точка перегиба. Теорема 17.5. (Достаточное условие точки перегиба) Пусть в точке x0 выполнены необходимые условия точки перегиба и пусть при переходе через эту точку является точкой перегиба. Без доказательства f '' (x) меняет знак, тогда точка x0 x