слайды к теме 12
advertisement
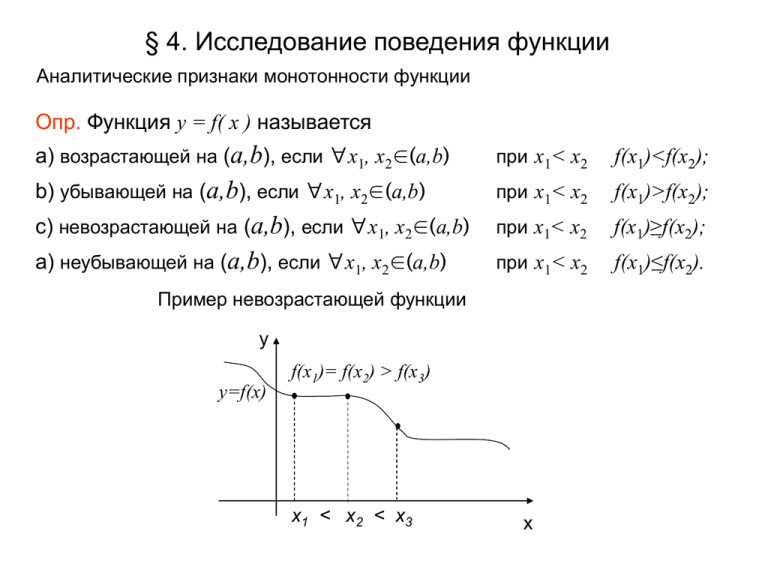
§ 4. Исследование поведения функции Аналитические признаки монотонности функции Опр. Функция y = f( x ) называется а) возрастающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)<f(x2); b) убывающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)>f(x2); c) невозрастающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)≥f(x2); а) неубывающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)≤f(x2). Пример невозрастающей функции y y=f(x) f(x1)= f(x2) > f(x3) x1 < x2 < x3 x Теорема 8. (Достаточное условие строгой монотонности) Пусть y=f(x) непрерывна на [a,b] и дифференцируема на (a,b), тогда если а) f '(x) >0 на (a,b), то f(x) возрастает на (a,b); b) f '(x) <0 на (a,b), то f(x) убывает на (a,b). Замечание. Обратное утверждение (необходимость) не верно. Контр пример: функция может быть возрастающей на (a,b) , а ее производная удовлетворяет нестрогому неравенству f '(x) ≥0 . y=x3 y '=3x2 y‘(0)=0 y y=x3 x Опр. Говорят, что f '(x) меняет знак в точке x0 , если существует окрестность точки x0: (x0 - δ, x0 + δ), в которой при x < x0 f '(x) сохраняет один знак, а при x > x0 – противоположный. Опр. Точки, в которых f '(x) =0 называются стационарными точками. Опр. Точки, в которых f критическими точками. '(x) =0 или не существует, называются Возможные варианты стационарных и критических точек y стационарные f '(x)=0 y экстр. x0 нет экстр. x0 x критические f '(x) экстр. x0 y нет экстр. x0 x критические f '(x) экстр. x0 нет экстр. x0 x Теорема 9. (1ый достаточный признак экстремума) Пусть y = f (x) непрерывна в интервале, содержащем критическую точку x0, дифференцируема во всех точках этого интервала, кроме может быть самой x0, тогда а) если при переходе слева направо через x0 производная f '(x) меняет знак с «+» на «-», то в точке x0 функция f (x) имеет максимум; b) если знак производной меняется с «-» на «+», то в точке f(x) имеет минимум. x0 функция Теорема 10. (2ой достаточный признак экстремума) Если в критической точке x0 функции y = f(x) обращается в ноль не только первая производная но и все последующие до (n - 1) - ой включительно, т.е. f '(x0)= f '' (x0)= f ''' (x0)=…= f (n-1)(x0)=0, а f (n)(x0)≠0, тогда x0 будет точкой экстремума, если n – четное; x0 не будет точкой экстремума, если n – нечетное. Характер экстремума определяется знаком f (n)(x0)≠0. При f (n)(x0)<0 - в x0 максимум, при f (n)(x0)>0 - в x0 минимум. Отыскание наибольшего и наименьшего значения функции на [a, b] Вспомним: Опр 10. b] выполняется неравенство f ( x ) ≤ f ( x0 ), то говорят, функция y = f ( x ) имеет в точке x0 глобальный максимум Если ∀ x ∈ [a, b] f ( x ) ≥ f ( x0 ), то в точке x0 глобальный минимум Если ∀ x ∈ [a, План 1. Найти критические точки с (f 2. Для каждой критической точки 3. Вычислить 4. Сравнить. (x)=0 ) xi f ( xi ), f ( a ), f ( b ) выяснить max или min