Подготовка к ЕГЭ. Решение задач группы С2

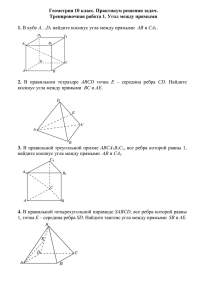
Подготовка к
ЕГЭ.
Решение задач
группы С2
(стереометрия)
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите расстояние от
точки C до AD1.
Треугольник ACD1 – равносторонний.
Из  ABC :
D1
С1
В1
А1
?
D
С
600
А
1
1
В
AC 2  12  12 ;
AC 2  2;
1
К
AC 2  AB 2  BC 2 ;
AC   2 ;
AC  2 .
Из  CKA
CK
sin 60 
AC
0
3 CK

2
2
6
CK 
2
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите угол между
прямыми AB1 и BС1 .
Заменим одну из заданных прямых BC1 на параллельную прямую AD1
.
D1
С1
В1
А1
D
a
А
∆B₁AD₁ - равносторонний и, значит, угол
B₁AD₁ равен 60°.
С
В
Угол между BC1 и АB₁ равен углу между
параллельной прямой AD1 и АB₁.
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите угол между
прямыми DA1 и BD1 .
Рассмотрим ортогональную проекцию AD₁ прямой BD1 на плоскость
ADD1 .
AD₁  DA₁
D1
С1
В1
А1
D
А
AD₁  DA₁
 DA₁  BD₁
TTT
С
П-Р
В
Искомый угол между прямыми DA₁ и BD1 равен 90°.
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите косинус угла
между прямыми AB и CA1 .
Заменим одну из заданных прямых AB на параллельную прямую B₁A1
.
Угол между AB и CА₁ равен углу между прямой C A1 и А₁B₁.
Из  CB1 В :
D1
a
А1
С1 B C 2  BB 2  CВ 2 ;
1
1
B1C 2  12  12 ;
В1
B1C 2  2;
2
B1C   2 ;
B1C  2 .
Из  A1 AC :
D
А
С .
В
С1
D1
А1
a
В1
2
D
А
!
С
В
Если вы получите
отрицательное значение
косинуса, - это говорит о
том, что угол тупой.
Вспомним, что в
стереометрии углом
между прямыми
называют острый.
Перейти к острому углу
просто.
cos a  m
В правильном тетраэдре ABCD точка E –середина ребра CD.
Найдите косинус угла между прямыми BC и AE.
Решение.
В ∆DBC проведем через точку E прямую ME // BC
Точка М – середина ребра DB.
Угол AEM - искомый.
D
Его можно найти из равнобедренного
треугольника MAE.
Из ∆ АВD :
E
0,5
M
0,5
A
1
В
С
Из ∆ СВD :
В правильном тетраэдре ABCD точка E –середина ребра CD.
Найдите косинус угла между прямыми BC и AE.
D
E
α
0,5
M
A
В
С
1. В правильной четырехугольной пирамиде SABCD, все
ребра которой равны 1, точка E – середина ребра SD.
Найдите тангенс угла между прямыми SB и AE.
Чертеж и подсказка
2. В правильной шестиугольной призме A….F₁, все ребра
которой равны 1, найдите косинус угла между прямыми AB₁
и BC₁.
Чертеж и подсказка
1. В правильной четырехугольной пирамиде SABCD, все
ребра которой равны 1, точка E – середина ребра SD.
Найдите тангенс угла между прямыми SB и AE.
В ∆DBS проведем через точку E прямую ME // BS
Угол AEM - искомый.
S
Из ∆ SВD :
Из ∆ AВD :
E
1
0,5
Из ∆ ADS:
D
1
A
С
M
1
Из ∆ AEM :
1
В
значит ∆ AEM прямоугольный
Ответ:
2. В правильной шестиугольной призме A….F₁, все ребра
которой равны 1, найдите косинус угла между прямыми AB₁
и BC₁.
E1
D1
F1
C1
A1
B1
1
E
D
F
A
1
B
C