справочный материал - Геометрия и математический анализ
advertisement
Настоящее пособие по выполнению контрольной работы по геометрии
(аналитическая геометрия
в пространстве)
для студентов заочного
отделения написано в соответствии с действующей программой
и
предназначено для студентов-заочников физико-математического факультета
педагогического университета. В пособии дается необходимый справочный
материал, приводятся подробно разработанные типовые примеры,
предлагаются задачи для самостоятельного решения. Варианты контрольных
работ приведены в таблице.
Контрольная работа выполняется в отдельной тетради в клеточку.
Записать номер и полную формулировку задачи. К задаче выполнить
рисунок, все пояснения к задаче писать подробно.
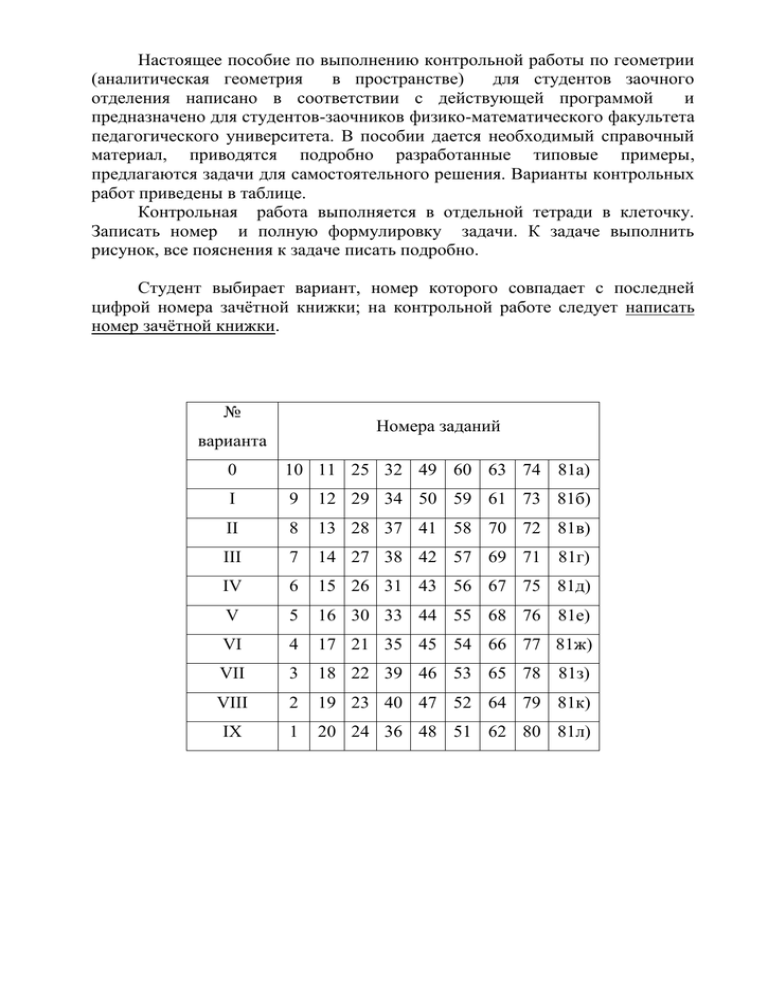
Студент выбирает вариант, номер которого совпадает с последней
цифрой номера зачётной книжки; на контрольной работе следует написать
номер зачётной книжки.
№
Номера заданий
варианта
0
10 11 25 32 49 60 63 74 81а)
I
9
12 29 34 50 59 61 73 81б)
II
8
13 28 37 41 58 70 72 81в)
III
7
14 27 38 42 57 69 71 81г)
IV
6
15 26 31 43 56 67 75 81д)
V
5
16 30 33 44 55 68 76 81е)
VI
4
17 21 35 45 54 66 77 81ж)
VII
3
18 22 39 46 53 65 78 81з)
VIII
2
19 23 40 47 52 64 79 81к)
IX
1
20 24 36 48 51 62 80 81л)
BAРИАНТ КОНТРОЛЬНОЙ РАБОТЫ С РЕШЕНИЕМ
Элементы векторной алгебры
Задача № 1. Найти при каких значениях m и n векторы а 1; m; 2 и
коллинеарны.
b 2; 3; n
Решение. Вектор b коллинеарн вектору а 0 , если
существует
единственное число такое, что: b = а .
Для данных векторов а и b это векторное равенство равносильно
2 ,
системе: 3 m ,
n 2 .
3
2
из которой находим 2, m , n 4 .
Итак, а 1; ;2 и b 2; 3; 4.
3
2
Задача № 2 Даны три некомпланарных вектора а , b , с . Доказать, что
векторы а + b , b + с , с а компланарны.
Решение. Воспользуемся условием компланарности трёх векторов:
если векторы а , b и с компланарны, а векторы а и b коллинеарны, то
существуют единственные числа , такие, что: с а b , т.е.
а + b = (b + с ) ( с а) .
(1)
Необходимо найти такие числа и , что выполняется соотношение (1),
преобразуем это соотношение
a ( 1) b (1 ) c ( ) 0 .
Сумма трёх некомпланарных векторов равна нуль – вектору, если
a ( 1) 0 , b (1 ) 0 , c ( ) 0 ,
из этих соотношений получаем, что 1 0 , 1 0 , 0 ,
откуда
1 1 , т.е. нашлись такие числа и , что выполняется
соотношение (1), значит, векторы а + b , b + с , с а компланарны.
Задача № 3. Точка N – центр тяжести (точка пересечения медиан)
треугольника АВС, а точка О – произвольная точка пространства.
1
3
Доказать, что ON (OA OB OC ) .
Решение. Пусть М – середина отрезка АВ. По правилу треугольника
имеем, что ON OС СN .
О
СМ – медиана (по условию), то
точка пересечения медиан
делит медиану в отношении
2:3, считая от вершины,т.е.
С
А
N
М
2
СN СМ , тогда
3
В
2
ON OС СМ . По правилу треугольника СМ СО ОМ , тогда имеем
3
2
2
1 2
ON OС СМ = OС (СО ОМ ) OС ОМ .
3
3
3
3
1
Так как М – середина отрезка АВ, то OМ (OА ОВ ) . Подставим
2
значение OМ в полученное соотношение, получим
1 2
1 2 1
1
ON OС ОМ OС (OА ОВ ) (OA OB OC ) .
3
3
3
3 2
3
Задача № 4. Найти объём треугольной пирамиды, построенной на
векторах OA, OB, OC , если ОА =5, ОВ =2, ОС =6, ОА ОВ 0 , ОА ОС 0 ,
ОВ ОС 8 .
Решение.
Так как по условию ОА ОВ 0 и
ОА ОС 0 , тогда
AOB 90o , AOС 90o , т.е. (ОА)(ОВС ) .
А
Искомый объём можно найти по формуле
1
V Н Sосн ,
3
В
О
где Н= ОА =5, площадь основания
можно найти следующим образом
С
Sосн SOBC
1
ОВ ОС sin BOС . Таким образом, имеем:
2
V
1
ОА ОВ ОС sin BOС .
6
Найдем sin BOС . По условию ОВ ОС 8 , следовательно, ОВ ОС ОВ
ОС сosBOС =8,
sin 1 cos2 1
1
6
Задача № 5.
8
2
,
26 3
5
5
10
.
3
3
Найти площадь параллелограмма, построенного на
ОС
4
5
.
9
3
Окончательно имеем, что V 5 2 6
сosBOС = 8 ОВ
тогда
векторах а =2 i + j +2 k и b =3 i +2 j +2 k .
Решение. Площадь параллелограмма, построенного на векторах а и b
равна модулю векторного произведения этих векторов.
Координаты векторов а и b равны: a 2; 1; 2, b 3; 2; 2; найдем
1 2
координаты вектора [ a, b ]
2 2
;
2 2
3 2
;
2 1
, или [ a , b ] 2; 2; 1.
3 2
Найдем длину вектора [ a , b ] :
[ a , b ] (2) 2 22 12 3 , т.е. искомая площадь S=3 (кв. ед.).
Задача № 6. Вычислить площадь треугольника, заданного координатами
своих вершин А(1; 1; 1) , В(2; 3; 4) , С (4; 3; 2) .
Решение. Площадь треугольника АВС равна половине площади
параллелограмма, построенного на
С
векторах
А
АВ и АС .
В
Найдем координаты векторов АВ и АС .
АВ 2 1; 3 1; 4 1 ; АС 4 1; 3 1; 2 1 или
АВ 1; 2; 3 , АС 3; 2; 1 .
Далее находим координаты вектора, являющегося векторным произведением
этих векторов
2 3
[ АВ, АС ]
2 1
1
2
Тогда S ABC [ АВ, АС]
;
1 3 1 2
;
= 4; 8; 4
3 1 3 2
1
16 64 16 24 (кв.ед.).
2
Можно было воспользоваться
треугольника:
S ABC
1
2
y2 y1
y3 y1
z2 z1
z3 z1
2
формулой для вычисления площади
z2 z1
z3 z1
x2 x1
x3 x1
2
x2 x1
x3 x1
y 2 y1
y3 y1
2
,
тогда подставив координаты вершин в формулу, получим:
4 1 2 1
2 1 4 1
1
1 3 1 3 1
16 64 16 24 (кв.ед.).
2
2 1 4 1
3 1 3 1
2 4 1 2 1
2
S ABC
2
2
Задача № 7. Вершинами треугольной пирамиды служат точки А(1; 2; 3) ,
B(0; 1; 1) , C (2; 5; 2) , D(3; 0; 2) . Найти объём пирамиды.
Решение. Эту задачу можно решить с использованием формулы
вычисления объема треугольной пирамиды, если вершинами пирамиды
служат точки А( x1; y1; z1 ) , B( x2 ; y2 ; z2 ) , C ( x3 ; y3 ; z3 ) , D( x4 ; y4 ; z4 ) :
x2 x1
1
V y2 y1
6
z2 z1
x3 x1
x4 x1
y3 y1
y4 y1 .
z3 z1
z4 z1
Другой способ решения задачи с использованием формулы объёма
параллелепипеда, объем
треугольной
пирамиды,
равен
1
1
Vпир Vпар ( а b c ) .
6
6
Найдём координаты векторов а , b , с :
а АВ {1;3;2} , b АC {1; 3;1} , c АD {2;2;5} , тогда
1 3 2
abс 1
2
3
1 1 (17) 3 (3) 2 (8) 17 9 16 24 .
2 5
1
6
Следовательно, V 24 4 .
Метод координат в пространстве
Задача № 8. Известны координаты вершин А, В, С параллелограмма
АВСD. Вычислить координаты вершины D, если А(2; 1; 1) , B(3; 1; 1) ,
C (0; 2; 3) .
Решение.
Из курса школьного курса геометрии известно, что
диагонали параллелограмма точкой пересечения делятся пополам. Для
нахождения
В
С
координат четвертой вершины D
К
воспользуемся формулой деления
отрезка в данном отношении:
А
x
D
x1 x2
;
2
y
y1 y 2
;
2
z
z1 z 2
2
Подставив в формулы координаты точек А и С найдем координаты точки К:
20
1 2 3
1 3
xK
1;
yK
; zK
1 , т.е. К(1; 3/2;-1).
2
2
2
2
Используя те же формулы вычислим координаты вершины D:
xK
xB xD 3 xD
y yD 1 yD
1 ; yK B
3/ 2 ;
2
2
2
2
zK
xD 1 ;
yD 4 ;
zB zD 1 zD
1 , тогда получим:
2
2
zD 3 , т.е. D (–1; 4; –3).
Задача № 9. В ПДСК заданы вершины треугольника АВС: А(4; 1; 2) ,
B(2; 0; 0) , C (2; 3; 5) . Найти длину биссектрисы AD его внутреннего угла А.
Решение.
Из курса школьного курса геометрии известно, что
С
биссектриса делит противолежащую
сторону на части, пропорциональные
длинам прилежащих сторон.
D
А
В
Найдем длины сторон АС и АВ:
AB (2 4) 2 (0 1) 2 (0 2) 2 4 1 4 3 ,
AC (2 4) 2 (3 1) 2 (5 2) 2 36 4 9 7 , т.е.
AB
AC
3
.
7
Найдем координаты точки D, используя формулы деления отрезка в
данном отношении:
xD
xB xC
yB yC
; yD
;
1
1
zD
z B zC
,
1
подставляя координаты точек в формулы, получим:
3
3
2 (2)
0 3
8 4
7
7 9
xD
; yD
3
3
10 5
10 ;
1
1
7
7
3
0 (5)
15 3
7
zD
3
10
2 .
1
7
Итак, координаты точки D(4 / 5; 9 / 10; 3 / 2) .
Уравнения плоскости и прямой в пространстве
Задача № 10. Написать уравнение плоскости, проходящей через точки
A(2; 1; 3) , B(5; 1; 2) и перпендикулярно плоскости : x 3 y 2 z 3 0 .
Решение.
В
n
А
Х
Для того чтобы написать уравнение плоскости надо знать координаты
трех компланарных векторов. Так как точки А, В, Х (произвольная точка)
принадлежат плоскости, то имеем векторы AB и AX образуют направляющее
подпространство плоскости . Рассмотрим вектор n перпендикулярный
плоскости , и так как , то n
.
Найдем
координаты
AB {3; 2; 1} ,
векторов
AX {x 2; y 1; z 3} ,
n {1;3;2} .
Три вектора компланарны, если их смешанное произведение равно
x2
нулю, т.е. ( AB, AX , n ) 3
1
y 1 z 3
2
3
1 0 ,
2
Раскроем определитель
: 4( x 2) ( y 1) 9( z 3) 2( z 3) 3( x 2) 6( y 1) 0 или
: 7 x 5 y 11z 52 0 .
Задача № 11 . Написать уравнение прямой а, проходящей через точку
2 x y z 3 0
A(1; 3; 4) параллельно прямой l:
.
x 3y z 1 0
Решение
Прямая а задана как
а
А
пересечение плоскостей и ,
найдем координаты
направляющего вектора
прямой l.
m
l
2 1 2 1
1 1
m
;
;
= 2; 3; 7.
3 1 1 1 1 3
Теперь напишем уравнение прямой а, проходящей через точку Аи
направляющий вектор m :
a:
Задача № 12 .
a:
x 2 y 1 z 1
и
4
1
1
x 1 y 3 z 4
.
2
3
7
Вычислить кратчайшее расстояние между прямыми
b:
x4 y2 z2
2
2
3
Решение.
Прежде чем найти расстояние между прямыми надо
определить
взаимное
расположение
прямых,
для
этого
найдем
направляющие векторы прямых и точки принадлежащие прямым.
Для прямой а: a a , a {4; 1; 1} , А(2; -1; 1),
для прямой b: b b , b {2; 2; 3} , В(-4; 2; -2), тогда AB {6; 3; 3}
Составим определитель из координат векторов a, b , AB :
6
( AB, a , b ) 4
2
3
3
1
1 18 6 24 6 12 36 90 .
2 3
Получили, что смешанное произведение векторов a, b , AB не равно
нулю, следовательно, эти векторы не компланарны, и следовательно, прямые
а и b скрещиваются.
b
b
Рассмотрим плоскость , проходящую
через прямую а параллельно прямой b и
B
плоскость , проходящую через
прямую b и параллельно прямой а.
b
A
Известно, что такие плоскости
a
существуют и определяются однозначно.
a
Расстояние между скрещивающимися прямыми равно расстоянию между
параллельными плоскостями и . Для нахождения этого расстояния
строим параллелепипед, как показано на рисунке и обозначим через V его
объем, тогда
( a, b) H
Vпар
S осн
AB, a , b
.
a, b
1
Найдем координаты вектора a, b
1
2 3
;
4 1
2 3
;
1
5; 10; 10 ,
2 2
4
и длину вектора
a, b
25 100 100 225 15 .
Следовательно, (a, b) H
90
6.
15
Задача № 13 . Составить уравнение проекции данной прямой l:
2 x y z 3 0
на данную плоскость : 7 x 5 y 11z 52 0 .
x y 2z 1 0
Решение.
Проекцией прямой l на плоскость
М
Х
является прямая l , которая
l
a
принадлежит плоскости и
n
плоскости . Плоскость проходит
через прямую l и перпендикулярно
плоскости .
l
Таким образом, напишем уравнение плоскости , которой компланарны
векторы a l , n , MX l . Найдем координаты векторов
2 1 2 1
1 1
;
;
a – направляющий вектор прямой l, a
3;3; 3;
1
2
1
2
1
1
n – вектор нормали плоскости , n 3;1; 1;
M (2 / 3; 5 / 3; 0) – точка прямой l, X ( x; y; z ) – произвольная точка прямой l,
MX x 2 / 3; y 5 / 3; z . Составим определитель из координат векторов
x 2/3
y 5/3 z
3
1
3
3
1 0 , раскроем определитель
3
: 3( x 2 / 3) 3( y 5 / 3) 9 z 3z 3( x 2 / 3) 9( y 5 / 3) 0 или
: 3 y 3z 5 0 .
3x y z 4 0
Таким образом, l : 3 y 3z 5 0 .
Поверхности второго порядка
Задача № 14 . Написать уравнение конической поверхности, если
направляющая в плоскости хОу задана уравнением : x 2 y 2 y 0 ,
вершина имеет координаты S(1; 0; 1).
x 2 y 2 y 0
Уравнение направляющей имеет вид :
z0 ,
Решение.
Найдем уравнение конической поверхности Ф,
Ф
пусть точка М (х; у; z) (отличная от точки S)
принадлежит конической поверхности Ф.
S
М
Тогда прямая SM пересечет направляющую
в точке Мо(хо; уо; zо).
Мо
Так как SM 0 и векторы SM и SM 0 коллинеарны (в силу определения
конической поверхности), то найдется такое число t, что SM 0 t SM , или в
координатах SM 0 {x0 1; y0 ; z0 1} , SM {x 1; y; z 1} , так как xOy , то
x0 1 t ( x 1)
y0 ty
z0 0 , тогда z 1 t ( z 1) , выразим x0 ; y0 ; z0 , получим
0
z 0 0
Точка
xz
x0 1 z
y
y0
.
1 z
t 1 z0
M 0 , подставим найденные координаты точки в уравнение
направляющей
:
y
xz y
0 , преобразуем
1 z 1 z 1 z
2
2
и найдем
уравнение поверхности Ф: ( x z ) 2 y 2 y(1 z ) 0 .
Задача № 15. Написать уравнение круговой цилиндрической поверхности,
x 7 3t
если известны уравнения её оси l : y 1 4t и координаты одной из её точек
z 3 2t
M1 (2; 1; 0) .
Решение.
Точки принадлежащие прямому круговому цилиндру
находятся на одинаковом расстоянии
от оси цилиндра,
поэтому чтобы
написать уравнение цилиндра Ф возьмем произвольную точку М (х; у; z),
лежащую на цилиндре и найдем расстояние от этой точки до оси цилиндра.
l
Мо
Ф
М1
М1
Н
Мо
l
p
Найдем расстояние от точки М1 до прямой l,
М
для этого воспользуемся формулой
M
M
;
p
0
1
S
( M 1 , l ) H пар
p
p
Итак, зная уравнение прямой l запишем координаты направляющего
вектора p {3;4;2} и координаты точки принадлежащей прямой Мо(7; 1; 3),
тогда M 0 M 1 {5;2;3} , найдем координаты вектора
2 3 5 3 5 2
M
M
;
p
;
;
8; 1; 14
0 1 4
2
3
2
3
4
подставим координаты векторов в формулу, получим
(M 0 , l )
82 12 (14) 2
32 4 2 2 2
3 29
3
29
Найдем расстояние от произвольной точки М лежащей на цилиндре до
прямой
l,
для
этого
воспользуемся
той
же
M 0 M ; p
(M , l ) H
3
M
.
0 M { x 5; y 2; z 3} , p {3;4;2}
p
формулой
y 2 z 3 x 5 z 3 x 5 y 2
;
;
M 0 M ; p 4
2
3
2
3
4
2( y 2) 4( z 3); 2( x 5) 3( z 3); 4( x 5) 3( y 2)
{2 y 4 z 8; 2 x 3z 1; 4 x 3 y 14} .
Длина вектора M 0 M ; p (2 y 4 z 8) 2 (2 x 3z 1) 2 (4 x 3 y 14) 2
22 x 2 13 y 2 25 z 2 16 yz 12 xz 24 xy 116 y 116 x 58 z 261
Подставляем в формулу нахождения расстояния
22 x 2 13 y 2 25 z 2 16 yz 12 xz 24 xy 116 y 116 x 58z 261
29
3 или
22 x 2 13 y 2 25z 2 16 yz 12 xz 24 xy 116 y 116 x 58z 261 3 29
22 x 2 13 y 2 25z 2 16 yz 12 xz 24 xy 116 y 116 x 58z 0
–
это
и
есть
уравнение цилиндрической поверхности.
Задача № 16.
Написать каноническое уравнение двуполостного
гиперболоида, если точки M 1 (3; 1; 2) , M 2 (2; 11; 3) , M 3 (6; 2; 15 ) принадлежат
поверхности Ф.
Решение. Каноническое уравнение двуполостного гиперболоида имеет
вид
x2 y2 z 2
1,
a 2 b2 c2
так как точки
M1; M 2 ; M 3
принадлежат Ф, то
координаты этих точек удовлетворяют уравнению этой поверхности,
поэтому
подставив
координаты
точек
в
уравнение
двуполостного
9 / a 2 1 / b 2 4 / c 2 1
2
2
2
гиперболоида получим систему: 4 / a 11 / b 9 / c 1 .
36 / a 2 4 / b 2 15 / c 2 1
Решив
систему
найдем
a 2 1; b 2 1 / 2; c 21 / 3 ,
каноническое уравнение двуполостного гиперболоида
x 2 2 y 2 3z 2 1.
теперь
запишем
x2 y2
z2
1 или
1 1/ 2 1/ 3
Задача № 17.
гиперболоида
Решение.
Найти прямолинейные образующие однополостного
2
x
y2 z2
1, проходящие через точку M 0 (6; 2; 8) .
9
4 16
Уравнения прямолинейных образующих для однополостного
x z
k1 a c l1 1
гиперболоида имеют вид x z
l1 k1 1
a c
Запишем
уравнения
прямолинейных
y
b
(1) и
y
b
x z
k 2 a c l2 1
x
z
l2 k 2 1
a c
образующих
x z
k1 3 4 l1 1
однополостного гиперболоида система (1): x z
l1 k1 1
3 4
для
y
b
(2).
y
b
данного
y
2
.
y
2
Так как точка M 0 , то подставив в систему значения x 6; y 2; z 8 ,
6 8
k1 3 4 l1 1
получим 6 8
l1 k1 1
3 4
2
2
или 2k1 l1 . Этому равенству удовлетворяют ,
2
2
например, числа k1 1; l1 2 . Подставим эти значения в систему (1) и после
4 x 12 y 3z 24 0
.
4 x 3 y 3z 6 0
преобразований получим систему:
Эти уравнения определяют прямолинейную образующую одного семейства,
проходящую через данную точку Мо поверхности Ф.
Проделав то же самое с системой (2), найдем уравнения прямолинейной
образующей
другого семейства,
4 x 3 z 0
.
y20
поверхности Ф:
проходящую через данную точку Мо
Задания для контрольной работы
1. Даны две вершины А(3;-4;-6), В(0;1;3) параллелограмма АВСD и точка
пересечения его диагонали Е(2;-1;5). Определить две другие вершины
этого параллелограмма.
2. Даны три вершины А(2;-2;2), В(-4;2;-5) и С(3;-2;-4) параллелограмма
АВСD. Найти его четвертую вершину, противоположную В.
3. Отрезок прямой, ограниченный точками А(5;-8;3) и В(11;3;-7), разделен
точками С, D,Е,F на пять равных частей. Найти координаты этих точек.
4. Даны вершины треугольника А(1;2;-1), В(2;-1;3) и С(-4;7;5). Вычислить
длину биссектрисы его внутреннего угла при вершине В.
5. Даны вершины треугольника А(2;-1;4), В(4;2;-6), С(-6;0;1). Вычислить
длину его медианы, проведенной из вершины А.
6. Вершины треугольника находятся в точках А(3;-4;7), В(-5;3;-2), С(1;2;-3)
7. Даны вершины треугольника А(1;2;-4), В(4;0;-10), С(-2;6;8). Вычислить
координаты центра тяжести этого треугольника.
8. Определить координаты концов отрезка, который точками С(2;0;2) и
D(5;-2;0) разделен на три равные части.
9. Даны вершины треугольника А(5;4;2), В(-5;-6;-2) и С(1;0;-1). Вычислить
длину его высоты, опущенной из вершины А на сторону ВС.
10. Даны вершины треугольника А(1;-1;2), В(5;-6;2) и С(1;3;-1). Вычислить
длину его высоты, опущенной из вершины В на сторону АС.
11. Вектор
x , перпендикулярный к векторам a3;1;3
и b 5;0;1, образует с
осью Oy тупой угол. Зная, что x 9 , найти его координаты.
12. Вектор m , перпендикулярный к оси Oz и к вектору a 5;5;2, образует
острый угол с осью Ox. Зная, что m
25 , найти его координаты.
13. Найти вектор x , зная что он перпендикулярен к векторам a3;2;0 и
x
2
i
3
j
5
k
20.
и
удовлетворяет
условию:
b 1;1;2
14. Вектор x , перпендикулярный к векторам a 2;1;0 и b 3;2;1, образует с
осью Oy острый угол. Зная, что x 4 , найти его координаты.
15. Вычислить
площадь
параллелограмма,
построенного
на
векторах
(
m
m
2
n
3
,
, ; n) / 4 .
a 2m 3n и b m 2n , если известно, что
16. Вычислить площадь треугольника АВС, если известно, что AB 2m n и
DC 3m n , если известно, что m 3 , n 4 , (m; n ) / 6 .
17. Дан треугольник АВС, в котором
А(1;1;-2), В(1;1;0), С(-1;3;0).
Вычислить длину его высоты АН.
18. Дан треугольник АВС, в котором
А(-1;1;2), В(1;1;0), С(2;6;-2).
Вычислить длину его высоты ВН.
19. Дан треугольник АВС, в котором
А(-1;1;2), В(1;1;0), С(2;6;-2).
Вычислить площадь треугольника АВС.
20. Дан треугольник АВС, в котором
А(6;5;-1), В(12;1;0), С(1;4;-5).
Вычислить площадь треугольника АВС.
21. Объём тетраэдра V=9, три его вершины находятся в точках А(-2;-1;3),
В(2;0;-1), С(3;-1;4). Найти координаты четвертой вершины D, если
известно, что она лежит на оси Oх.
22. Вычислить объем тетраэдра, вершины которого находятся в точках
А(2;-1;0), В(5;4;3), С(3;1;-1) и D(4;-1;3).
23. Даны вершины тетраэдра: А(-2;3;0), В(4;2;-1), С(5;3;6), D(-4;-5;9). Найти
длину его высоты, опущенной из вершины D.
24. Объём тетраэдра V=7, три его вершины находятся в точках А(-2;0;-1),
В(3;-1;1), С(2;-1;4). Найти координаты четвертой вершины D, если
известно, что она лежит на оси Oу.
25. Даны вершины тетраэдра: А(7;5;-1), В(0;-2;1), С(2;-2;4), D(-4;1;3). Найти
длину его высоты, опущенной из вершины В.
26. Найти объём и высоту призмы АВСА/В/С/, зная координаты вершин
А(1;5;-2), В(4;1;1), С(-3;0;1), А/(2;-1;3).
27. Даны вершины тетраэдра А(0;0;0), В(1;-3;0), С(1;2;0), D(0;0,5). Найти
длину высоты этого тетраэдра, проведенной из вершины А.
28. Найти
полную поверхность и высоту призмы АВСА/В/С/, зная
координаты вершин А(1;5;-2), В(4;1;1), С(-3;0;1), А/(2;-1;3).
29. Вычислить объем параллелепипеда
АВСDА/В/С/D/, если А(0;1;-1),
В(-1;3;5), D(-1;3;4), А/(0;51-2).
30. Объём тетраэдра V=5, три его вершины находятся в точках А(2;1;-1),
В(3;0;1), С(2;-1;3). Найти координаты четвертой вершины D, если известно,
что она лежит на оси Oу.
31. Составить уравнение плоскости, которое проходит через точку М1(3;-2;-7)
параллельно плоскости 2x-3z+5=0.
32. Составить уравнение плоскости, которая проходит через начало
координат перпендикулярно к двум плоскостям: 2x-y+3z-1=0, x+2y+z=0.
33. Составить уравнение плоскости, которая проходит через точку М1(2;-1;1)
перпендикулярно к двум плоскостям: 2x-z+1=0 и y=0.
34. Составить уравнение плоскости, которая проходит через две точки
М1(1;-1;-2) и М2(3;1;1) перпендикулярно к плоскости x-2y+3z-5=0.
35. Написать уравнение плоскости, проходящей через точки М1(1;4;-1),
М2(-13;2;-10) и отсекает на осях абсцисс и аппликат отличные от нуля
отрезки одинаковой длины.
36. Составить уравнение плоскости, отсекающей на оси Oz отрезок с= –5 и
перпендикулярной к вектору n 2;1;3.
37. Составить
уравнение
плоскости, проходящей перпендикулярно к
плоскости 2x-2y+4z-5=0 и отсекающей на координатных осях Ox и Oy
2
3
отрезки a= –2, b= .
38. Составить
уравнение
плоскости,
проходящей
через
точку
В
перпендикулярно прямой АВ, зная, что А(1;3;-2), В(7;-4;4). Система
координат прямоугольная декартова.
39. Написать уравнение плоскости, проходящей через линию пересечения
плоскостей
x+3y+5z–4=0,
x–y–2z+7=0
и
параллельно
плоскости
3x+2y+3z+1=0.
40. Написать уравнение плоскости, проходящей через линию пересечения
плоскостей
x+3y+5z–4=0 и x–y–2z+7=0
и перпендикулярно плоскости
2x–y+z–3=0.
41. Даны уравнения параллельных плоскостей 4x+6y+2z–7=0; 2x+3y+z+5=0.
Написать уравнение плоскости, проходящей посередине между данными
плоскостями.
42. В ПДСК даны уравнения плоскостей двух граней куба: x–2y–2z+4=0,
2x+2y–z–13=0
и координаты его центра М0(1;1;-2). Найти уравнения
плоскостей остальных граней куба.
43. Написать уравнение плоскости, проходящей через точки М(2;0;0) и
Р(0;2;0) и образующий угол 450 с плоскостью x+y+z+1=0,
44. Найти уравнения плоскостей, проходящих через начало координат,
перпендикулярных к плоскости 5x–2y+5z–10=0 и образующих с плоскостью
x–4y–8z+12=0 угол 450.
45. На оси Oz найти точку, равноудаленную от точки М(1;-2;0) и от
плоскости 3x–2y+6z–9=0.
46. На оси Oу найти точку, равноудаленную от точки М(1;0;1) и от плоскости
x+y+z+4=0.
47. Найти угол между плоскостями, проходящими через точку М(1; –1; –1),
одна из которых содержит ось Ох, а другая – ось Оz.
48. Найти
расстояние
между параллельными плоскостями x–2y+2z–6=0
и x–2y+2z+18=0 .
49. На оси Oу найти точку, равноудаленную от двух плоскостей, заданных
уравнениями x+2y–2z–1=0, 3x+5=0.
50. На оси Oz найти точку, равноудаленную от двух плоскостей, заданных
уравнениями x+4y–3z–2=0, 5x+z+8=0.
51. Найти проекцию точки Р(2;-1;3) на прямую x=3t, y=5t–7, z=2t+2.
52.Найти точку Q , симметричную точке Р(4;1;6) относительно прямой:
x y 4 z 12 0
2 x y 2 z 3 0
53. Найти точку Q, симметричную точке Р(2; –5;7) относительно прямой,
проходящей через точки М1(5;4;6) и М2(–2; –17; –8).
54. Найти проекцию точки Р(5;2; –1) на плоскость 2x–y+3z+23=0.
55. Найти проекцию точки С(3;–4;–2) на плоскость, проходящую через
параллельные прямые:
x 15 y 6 z 3
,
13
1
4
x2 y 3 z 3
13
1
4
56. Найти точку Q, симметричную точке Р(3;–4; –6) относительно плоскости,
проходящей через М1(–6;1; –5), М2(7; –2; –1) и М3(10; –7;1).
57.Найти точку Q симметричную точке Р(–3;2;5) относительно плоскости,
проходящей через прямые:
x 2 y 3z 5 0,
x 2 y 4z 3 0
3 x y 3 z 7 0,
5 x 3 y 2 z 5 0
58. Составить уравнение прямой, которая проходит через точку М1(–1;2; –3)
перпендикулярно к вектору a 6;2;3 и пересекает прямую:
x 1 y 1 z 3
.
3
2
5
59. Составить уравнение прямой, которая проходит через точку М1(–4; –5;3)
и пересекает две прямые:
x 1 y 3 z 2
,
3
2
1
x 2 y 1 z 1
.
2
3
5
60. Составить параметрические уравнения общего перпендикуляра
x 3t 7
x t 1
y 2t 4
прямых, заданных уравнениями:
и y 2t 9
z 3t 4
z t 12
двух
61. Вычислить
кратчайшее
x7 y4 z3
;
3
4
2
расстояние
между
двумя
прямыми:
x 21 y 5 z 2
.
6
4
1
62. Вычислить кратчайшее расстояние между двумя прямыми:
x 3t 7
x t 1
y 2t 4
и y 2t 9
z 3t 4
z t 12
63. Вычислить кратчайшее расстояние между двумя прямыми:
x 2t 4
x 4t 5
y t 4
и y 3t 5 .
z 5t 5
z 2t 5
64. Вычислить кратчайшее расстояние между двумя прямыми:
x 5 y 5 z 1
;
3
2
2
x 6t 9, y=–2t, z=–t+2.
65. Вычислить кратчайшее расстояние между двумя прямыми:
x 1 y 2 z 1
;
2
4
3
x 2 y 1 z 3
.
3
2
4
66. Вычислить кратчайшее расстояние между двумя прямыми:
x t 3
y 2t 1
и
z 4
x 3y z 0
x y z 4 0
67. Найти проекцию точки М(–1;2;0) на плоскость x y 2 z 1 0 .
68. Составить уравнение проекции данной прямой
x 1 y 1 z 1
2
0
1
на
плоскость хОу.
69. Составить уравнение проекции данной прямой
x y 2z 3 0
на
2x y z 1 0
плоскость хОу.
70. Найти точку, симметричную точке М(1;5;2) относительно плоскости
2 x y z 11 0 .
71.Составить уравнение цилиндра, образующие которого параллельны
x 2 y 2 9,
вектору 2;3;4, а направляющая дана уравнениями:
z 1
72. Составить
уравнение
цилиндра,
x 2 y 2 z,
х y z 0,
уравнениями:
направляющая
которого
дана
а образующие перпендикулярны к
плоскости направляющей.
73. Составить уравнение кругового цилиндра, походящего через точку
x 3t 1
S(2;-1;1), если его осью служит прямая y 2t 2 .
z t 2
74. Написать уравнение цилиндра вращения, проходящего через точку
xt
М0(1;-2;1), осью которого служит прямая: y 2t 1 .
z 2t 3
75. Написать уравнение цилиндрической поверхности, если направляющая
2 y 2 3z 2 1
задана уравнениями
, а образующая параллельна вектору с
x 1
координатами a1;2;3 .
76. Составить уравнение конической поверхности, вершина которого
находится в начале координат, а направляющая дана уравнениями:
x2 y2
2 2 1
a
.
b
z c
77. Составить уравнение конической поверхности, вершина которого
находится в точке S(0;0;1), а направляющая дана уравнениями:
x2 y2
1,
25 9
z 0,
78. Составить уравнение конической поверхности,
находится
в
точке
x 2 y 2 z 2 1
x yz 0
S(3;–1;–2),
а
направляющая
вершина которого
дана
уравнениями:
79. Ось Oz является осью кругового конуса с вершиной в начале координат,
точка М1(3;-4;7) лежит на его поверхности. Составить уравнение этой
конической поверхности.
80.
Ось Oy является осью кругового конуса с вершиной координат, его
образующие наклонены под углом в 600 к оси Oy. Составить уравнение этой
конической поверхности.
81.
Написать уравнение
эллипсоида, оси которого совпадают с осями
координат и который проходит через точку М(3;1;0) и пересекает плоскость
x2 z 2
1.
хOz по эллипсу
16 4
82. Написать уравнение
эллипсоида, оси которого совпадают с осями
координат и который проходит через точку М(3;1;0) и пересекает плоскость
y2 z2
1.
yOz по эллипсу
25 16
83. Даны вершины эллипсоида А1(8;0;0); А2(-2;0;0). Написать уравнение этого
эллипсоида, зная, что плоскость yOz пересекает его по эллипсу: x=0,
y2 z2
1.
9
4
84. Оси симметрии однополостного
гиперболоида Ф служат осями
ортонормированного репера. Написать уравнение этого гиперболоида, если
25 x 2 16 z 2 144
он проходит через линию
и точку М1(3; 4;3).
х y
85. Написать каноническое уравнение однополостного
гиперболоида Ф,
проходящего через точку M ( 5 ;3;2) и пересекает плоскость xOz по гиперболе
x2 z2
1.
5
4
86. Написать каноническое уравнение однополостного гиперболоида Ф, если
поверхность пересекает плоскость xOу по окружности
плоскость xOz по гиперболе
x2 z 2
1.
9 10
x2 y 2 9 , а
87. Написать каноническое уравнение двуполостного гиперболоида Ф, если
точки M1 (3;1;2) , M 2 (2; 11;3) , M 3 (6;2; 15 ) лежат на данной поверхности.
88. Определить вид линии пересечения однополостного гиперболоида
x2 y2 z 2
1 плоскостью, проходящей через точку (0;0;14) параллельно
4
9 36
плоскости 9 x 6 y 2 z 5 0 .
89.
Определить вид линии пересечения эллиптического параболоида
y2
x
2 z с плоскостью z 4 0 .
9
2
90. Определить вид линии пересечения гиперболического параболоида
x 2 4 y 2 z с плоскостью x 2 y 3 0 .
91.
Найти
уравнения
прямолинейных
образующих
поверхности
x2 y2 z 2
1, проходящих через точку М0(5;3;2).
25 9
4
92.
Написать
уравнения
двух
систем
прямолинейных
образующих
однополостного гиперболоида x 2 9 y 2 z 2 9 и определить те из них,
которые проходят через точку M (3; 1 / 3;1) .
93. На гиперболическом параболоиде
x2 y 2
2 z,
8
2
найти уравнения
прямолинейных образующих параллельных плоскости 6x+4y–8z+1=0.
94.
Найти
уравнения
прямолинейных
образующих
поверхности
x2 y2 z 2
1, проходящих через точку М0(1;3;2).
4
9 25
95.
Написать уравнение плоскости, параллельной данной плоскости
: x y z 5 0 и пересекающей параболоид
x2 z 2
2y
9
4
по двум
прямолинейным образующим.
97.
Написать
уравнения
прямолинейных
4 x 2 y 2 16 z , пересекающиеся в точке М(2;0;1).
образующих
параболоида
98.
Написать
уравнения
прямолинейных
образующих
гиперболоида
x2 y 2 z 2
1 , пересекающиеся в точке М(6;2;8).
9
4 16
99.
Написать
уравнения
прямолинейных
образующих
гиперболоида
x2 y 2 z 2
1 , перпендикулярные оси Оу.
9
4 16
100. Найти прямолинейные
образующие гиперболического параболоида
x 2 y 2 4 z , параллельные плоскости x+y+z –1=0.
СПРАВОЧНЫЙ МАТЕРИАЛ
ОПЕРАЦИИ НАД ВЕКТОРАМИ
В
A( x1 , y1 , z1 )
B( x2 , y2 , z3 )
А
AB{ x2 x1 ; y2 y1 ; z2 z1 }
координаты вектора
СЛОЖЕНИЕ ВЕКТОРОВ
b
а
b b1 , b2 , b3
а b
а b
а
а b c
аа1 , a2 , a3
c а1 b1 , a2 b2 , a3 b3
а b d
d а1 b1 , a2 b2 , a3 b3
ВЫЧИТАНИЕ
ВЕКТОРОВ
b
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
а b
a
b
1.
2. а b , если 0
3. а b , если 0
b b1 , b2 , b3
а b
a b1 , b2 , b3
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
аа1 , a2 , a3 , b b1 , b2 , b3
а b = а · b сos ( а , b )
а b a1b1 a2b2 a3b3
a b a1b1 a2b2 a3b3 0
a а 2 а12 а22 a32
b
угол между векторами
а
a b
cos
ab
a1b1 a2 b2 a3b3
a12 a22 a32 b12 b22 b32
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
аа1 , a2 , a3 , b b1 , b2 , b3
a b с :
c
a
b
sin(
a
, b) ,
1.
a b с
2. с a , c b ,
{
a
3. , b , c } правая тройка
a
с 2
b2
S a b
с
a3
b3
,
a1
a3
b1
b3
,
a1
b1
a2
b2
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
Модуль векторного произведения
b
S
а
равен площади параллелограмма,
построенного на этих векторах
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ab c (a b ) c
аа1 , a2 , a3
b b1 , b2 , b3
с с1 , с2 , с3
с
Н
b
ВЫРАЖЕНИЕ СМЕШАННОГО
ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
В КООРДИНАТАХ
а
a1 a2
(ab c ) b1 b2
c1
c2
a3
b3
c3
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ СМЕШАННОГО
ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Модуль смешанного произведения равен
объёму параллелепипеда,
построенного на этих векторах
a1 a2 a3
Vпар а b c b1 b2
c1
c2
b3
c3
D
Формула для вычисления объёма
тетраэдра, заданного координатами
вершин A( xA , y A , z A ) , B( xB , yB , zB ) ,
C ( xC , yC , zC ) , D( xD , yD , zD )
А
В
xB x A
С
1
Vтетр Vпар yB y A
6
zB z A
xC x A
xD x A
yC y A
yD y A
zC z A
zD z A
ПРЯМОУГОЛЬНЫЕ ДЕКАРТОВЫ КООРДИНАТЫ
М
z
B
A( x1 , y1 , z1 )
B( x2 , y2 , z3 )
A
k
y
i
j
AB{ x2 x1 ; y2 y1 ; z2 z1 }
координаты вектора
x
AB ( x2 x1 )2 ( y2 y1 )2 ( z 2 z1 )2
длина вектора (расстояние между точками)
ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ
АМ
МВ
М
A
М ( x, y , z )
АМ
МВ
x1 x2
1
y y 2
y 1
1
z z 2
z 1
1
x
A( x1 , y1 , z1 )
B( x2 , y2 , z3 )
В
x1 x2
2
y y2
y 1
2
z z
z 1 2
2
x
1
ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Ax By Cz D 0
Общее уравнение плоскости
n
z
M 0 ( x0 , y0 , z0 )
n{ A, B, C}
М0
r0
(r r0 ) n 0
М
r
у
О
х
A( x x0 ) B( y y0 ) C ( z z0 ) 0
Уравнение плоскости, проходящей
через точку и перпендикулярный вектор
M 0 ( x0 , y0 , z0 )
a{a1 , a 2 , a3 }
b{b1 , b2 , b3 }
b
a
z
М0
r r0 a b
(r r0 , a, b ) 0
М
r0
r
О
у
х
x x0 a1 b1 ;
y y 0 a 2 b2 ;
z z a b .
0
3
3
Параметрическое уравнение
a1
a2
a3
b1
b2
b3
x x0
y y0
z z0
0
Уравнение плоскости, заданной
точкой и направляющим
подпространством
ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
М1
z
M 0 ( x0 , y0 , z0 )
М
M1 ( x1 , y1 , z1 )
M 2 ( x2 , y2 , z2 )
М0
М2
О
у
х
уравнение плоскости, проходящей через три точки
x x0
y y0
z z0
x1 x0
y1 y0
z1 z 0 0
x2 x0
y 2 y0
z 2 z0
z
M 0 (а,0,0)
М2
M1 (0, b,0)
М1
M 2 (0,0, c)
x y z
1
a b c
у
О
уравнение плоскости
в отрезках
М0
х
М
п0
О
х
z
n0 (сos , сos , сos )
(O, ) p
р
(r r0 , n ) 0
r
у
x cos y sin z cos p 0
нормированное уравнение плоскости
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ
A1
: A1 x B1 y C1 z D1 0 ; A
A2
: A2 x B2 y C2 z D2 0
Плоскости совпадают
rgA rgA 1
Плоскости параллельны
B1
B2
C1
A
; A 1
C2
A2
B1
B2
C1 D1
C2 D2
rgA 1; rgA 2
Плоскости пересекаются по прямой
rgA rgA 2
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
: A1 x B1 y C1 z D1 0 ,
: A2 x B2 y C2 z D2 0 ,
n1 n2
cos
n1 n2
n1{A1; B1; C1}; n1
n2{A2 ; B2 ; C2}; n2
A1 B1 A2 B2 A3 B3
A12 B12 C12 A22 B22 C22
: A1 A2 B1B2 C1C2 0
:
A1 B1 C1
A2 B2 C2
n1
n2
ПРЯМАЯ В ПРОСТРАНСТВЕ
а : A1 x B1 y C1 z D1 0
а : A2 x B2 y C2 z D2 0
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
( ││ ) уравнение прямой как пересечение двух плоскостей
z
М0
М
a
M 0 ( х0 , y0 , z0 ) a
a{a1 , a2 , a3 } а
r0
r
М1
О
у
х
r r0 ta
векторное уравнение прямой
x x0 a1t ;
y y0 a2 t ;
z z a t.
0
3
параметрическое
уравнение прямой
x x0 y y0 z z0
a1
a2
a3
каноническое уравнение
прямой
M 0 ( x0 , y0 , z0 ) а
M1 ( x1 , y1 , z1 ) а
x x0
y y0
z z0
x1 x0 y1 y0 z1 z0
уравнение прямой,
проходящей через 2 точки
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ
ПРЯМЫХ В ПРОСТРАНСТВЕ
a
а
M1 ( х1, y1, z1 ) a
М1
a{a1 , a2 , a3 } а
b
M 2 ( х2 , y2 , z2 ) b
b{b1 , b2 , b3} b
М2
b
M
M
a
Прямые a, b скрещиваются (векторы 1 1 , , b – некомпланарны )
x2 x1
y2 y1
z2 z1
a1
a2
a2
b1
b2
b3
0
Прямые a, b принадлежат одной плоскости
M
M
a
(векторы 1 1 , , b – компланарны )
x2 x1 y2 y1 z2 z1
a1
a2
a2 0
b1
b2
b3
Прямые пересекаются
a
параллельны
М1
b
a
М2
М1
совпадают
a
М1
М2
М2
a
rg 1
b1
a2
b2
a3
2
b3
a
rg 1
b1
a2
b2
a3
1
b3
x x
rg 2 1
a1
y2 y1
a2
z2 z1
1
a3
УГОЛ МЕЖДУ ПРЯМЫМИ
а
M1 ( х1, y1, z1 ) a
a{a1 , a2 , a3 } а
М1
a
M 2 ( х2 , y2 , z2 ) b
b{b1 , b2 , b3} b
М2
b
b
a b
cos
a b
a1b1 a2b2 a3b3
a12 a22 a32 b12 b22 b32
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
M 0 ( х0 , y0 , z0 ) d
p { p1 , p2 , p3}
d
Прямая пересекает плоскость
d
p
Ap1 Bp 2 Cp3 0
Р
M0
Прямая параллельна плоскости
p
d
M0
Ap1 Bp 2 Cp3 0
Ax0 By 0 Cz0 D 0
Прямая лежит в плоскости
M0
d
p
Ap1 Bp2 Cp3 0
Ax0 By 0 Cz0 D 0
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ
a{a1 , a2 , a3 }
M 2 ( х2 , y2 , z2 ) b ; b{b1 , b2 , b3}
M1 ( х1, y1, z1 ) a ;
а
b
Прямые параллельны
М2
Н
M
M
1
2; a
S
(a; b) ( M 2 , a) H пар
a
a
М1
a
Прямые скрещиваются
b
b
М2
( a, b) H
М1
a
Vпар
Sосн
M 1M 2 , a , b
a, b
а
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
М0
: Ax By Cz D 0
M 0 ( x0 , y0 , z0 )
d
d ( M 0 , )
Ax0 By 0 Cz0 D
A2 B 2 C 2
Расстояние от точки до плоскости
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
а11х 2 a22 y 2 a33 z 2 2а12 ху 2а23 уz 2а13 хz
2а10 х 2a20 y 2a30 z а00 0
Общее уравнение поверхности второго порядка
КОНИЧЕСКИЕ ПОВЕРХНОСТИ
Вместе с каждой точкой М
отличной от точки S, поверхность
содержит всю прямую МS
КОНУС ВТОРОГО ПОРЯДКА
x2 y 2 z 2
2 2 0
2
a
b
c
ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
образующая
Вместе с каждой точкой М
содержит всю прямую,
проходящую через М, параллельно
данному вектору p
М
p
Направляющая
ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
x2 y 2
1
a2 b2
x2 y 2
1
a 2 b2
y 2 2 px
ЭЛЛИПСОИД
x2 y 2 z 2
1
a 2 b2 c2
Каноническое
уравнение
трехосного эллипсоида
A1 (a,0,0) , A2 (a,0,0)
B1 (0, b,0) , B2 (0,b,0) C1 (0,0, c) , C2 (0,0,c)
Вершины эллипсоида
а, b, с – полуоси эллипсоида
а=b
2
2
а=b=с
2
x y z
1
a2 a2 c2
Эллипсоид вращения
x2 y 2 c2 a2
сфера
ГИПЕРБОЛОИДЫ
x2 y 2 z 2
2 2 1
2
a b c





