Лекция 3
Кинетическая и потенциальная энергия. Закон сохранения момента
импульса.
§16. Скалярное произведение векторов.
§17. Механическая работа. Мощность.
§18. Кинетическая энергия тела и ее связь с совершенной над ним работой.
§19.Консервативные и диссипативные силы. Потенциальная энергия.
§20.Момент силы относительно точки, относительно оси.
§21.Момент импульса материальной точки относительно точки,
относительно оси.
§22.Момент импульса твердого тела относительно неподвижной оси
вращения. Момент инерции.
§23.Расчет моментов инерции некоторых твердых тел относительно их
осей симметрии. Теорема Штейнера.
§24.Закон сохранения момента импульса.
§16. Скалярное произведение векторов.
Скалярное произведение векторов 𝑎
⃗⃗⃗ и 𝑏⃗ называют число, равное
произведению длин этих векторов на косинус угла между ними.
⃗⃗⃗ ∙ ⃗⃗⃗
𝑎
𝑏 = 𝑎𝑏 cos 𝜃
(1)
⃗⃗⃗ .
где 𝜃 - угол между векторами 𝑎
⃗⃗⃗ и 𝑏
При умножении вектора самого на себя получим квадрат его модуля:
⃗⃗⃗
𝑎 ∙𝑎
⃗⃗⃗ = 𝑎𝑎 cos 0 = 𝑎2
(2)
Скалярное произведение двух взаимно перпендикулярных векторов 𝑎
⃗⃗⃗ и 𝑏⃗
равно нулю.
Скалярное произведение и его свойства
Существуют свойства скалярного произведения, которые применимы для
векторов 𝑎 , 𝑏⃗ и 𝑐
:
1
1.
2.
3.
4.
⃗⃗⃗ = 𝑏⃗ ∙ 𝑎 ;
коммутативность 𝑎
⃗⃗⃗ ∙ 𝑏
⃗⃗⃗ ) ∙ 𝑐 = 𝑎
⃗⃗⃗ ∙ 𝑐 ;
дистрибутивность ( ⃗⃗⃗
𝑎 +𝑏
⃗⃗⃗ ∙ 𝑐 + 𝑏
⃗⃗⃗ ) = 𝜆(𝑎
⃗⃗⃗ ), 𝜆 - любое число;
сочетательное свойство (𝜆 𝑎
⃗⃗⃗ ∙ 𝑏
⃗⃗⃗ ∙ 𝑏
скалярный квадрат всегда больше нуля 𝑎
⃗⃗⃗ ∙ 𝑎
⃗⃗⃗ ≥ 0, где ⃗⃗⃗
𝑎 ∙𝑎
⃗⃗⃗ = 0 в
том случае, когда 𝑎
⃗⃗⃗ нулевой.
Скалярное произведение в координатах
Вычисление скалярного произведения можно производить через
координаты векторов в заданной плоскости или в пространстве.
При вычислении на плоскости скалярного произведения заданных
векторов 𝑎
⃗⃗⃗ = (𝑎𝑥 , 𝑎𝑦 ) и ⃗⃗⃗
𝑏 = (𝑏𝑥 , 𝑏𝑦 ) в декартовой системе, используют:
⃗⃗⃗
𝑎 ∙ ⃗⃗⃗
𝑏 = 𝑎𝑥 𝑏𝑥 + 𝑎𝑦 𝑏𝑦
(3)
для трехмерного пространства применимо выражение:
⃗⃗⃗ = 𝑎𝑥 𝑏𝑥 + 𝑎𝑦 𝑏𝑦 + 𝑎𝑧 𝑏𝑧
⃗⃗⃗ ∙ 𝑏
𝑎
(4)
Скалярный квадрат вектора равен сумме квадратов его координат в
пространстве 𝑎
⃗⃗⃗ ∙ 𝑎
⃗⃗⃗ = 𝑎𝑥2 + 𝑎𝑦2 + 𝑎𝑧2 и на плоскости ⃗⃗⃗
𝑎 ∙𝑎
⃗⃗⃗ = 𝑎𝑥2 + 𝑎𝑦2 ,
соответственно.
§17. Механическая работа. Мощность.
Элементарной называется работа, совершаемая силой при бесконечно
малом перемещении тела (материальной точки). Пусть 𝑑𝑟⃗⃗ – бесконечно
малое перемещение тела, на которое действует сила ⃗⃗⃗
𝐹 .Тогда элементарная
работа, совершаемая силой ⃗⃗⃗
𝐹 , определяется как
𝑑𝐴 = ⃗⃗⃗
𝐹 ∙ 𝑑𝑟⃗⃗ = 𝐹 cos 𝛼 ∙ 𝑑𝑟
(5)
где 𝛼 - угол между направлением силы и направлением перемещения.
Единицей измерения работы является джоуль : Дж = н∙м .В зависимости от
угла между силой и перемещением (из-за знака cos 𝜃 ) работа может быть
𝜋
положительной, отрицательной и нулевой. При 𝛼 =
работа равна нулю.
2
Последнее обстоятельство особенно отчетливо показывает, что понятие
работы в механике существенно отличается от обыденного представления о
2
работе. Например, для того, чтобы перенести тяжелый груз по
горизонтальному пути, человек затрачивает много усилий, т.е. «совершает
работу». Однако работа как механическая величина в этом случае равна
нулю.
Если тело, к которому приложена сила, описывается моделью
материальной точки или двигается поступательно, но при этом движение не
прямолинейно или/и сила не постоянна, то для нахождения работы силы
траекторию поступательного движения тела надо разбить на малые участки,
в пределах которых силу можно считать постоянной, а сами участки прямолинейными. Работа A будет приблизительно равна сумме работ 𝐴𝑖
𝐹𝑖 ∆𝑟𝑖 cos 𝛼𝑖 = ⃗⃗𝐹𝑖 ⃗⃗⃗⃗
∆𝑟𝑖
, совершенных на каждом участке A≈
=
∑ ⃗⃗𝐹𝑖 ⃗⃗⃗⃗
∆𝑟𝑖 .
Для достижения точного равенства надо длину участков устремить к нулю, а
их количество к бесконечности. При этом в сумме заменим конечные
величины бесконечно малыми ⃗⃗⃗⃗
∆𝑟𝑖 → ⃗⃗⃗⃗
𝑑𝑟 , ⃗⃗𝐹𝑖 → ⃗⃗⃗
𝐹 , 𝐴𝑖 → 𝛿𝐴 и рассмотрим
предел суммы, при 𝑖 → ∞ , который по определению является интегралом.
То есть работа равна:
(2)
(2)
⃗⃗⃗⃗
𝐴12 = ∫(1) 𝑑𝐴 = ∫(1) 𝐹 ∙ 𝑑𝑟
(6)
Это определение механической работы . Работа по определению является
скаляром и в общем случае зависит от траектории движения материальной
точки (тела) из положения (1) в положение (2).
Пусть на тело действует одновременно несколько сил, результирующая
которых равна ⃗⃗⃗
𝐹 = ∑𝑖 ⃗⃗⃗
𝐹 𝑖 . Из дистрибутивности скалярного произведения
векторов (свойство 2) вытекает , что работа совершаемая результирующей
⃗⃗⃗⃗ может быть представлена в виде:
силой на 𝑑𝑟
⃗⃗⃗⃗ = ∑𝑖 ⃗⃗⃗
⃗⃗⃗⃗ = ∑𝑖 𝑑𝐴𝑖
𝐴 = (∑𝑖 ⃗⃗⃗
𝐹 𝑖 )𝑑𝑟
𝐹 𝑖 𝑑𝑟
(7)
Работа результирующей нескольких сил равна алгебраической сумме работ,
совершаемых каждой из сил в отдельности.
В системе СИ работа измеряется в джоулях, Дж= Н ∙ м .
Для характеристики работы, совершаемой в единицу времени, в механике
используется понятие мощности. Мощностью ( мгновенной мощностью )
называется скалярная величина равная элементарной работе, отнесенной к
3
бесконечно малому промежутку времени dt, за которое она была
совершена:
𝑃=
𝛿𝐴
=
⃗⃗⃗⃗⃗
⃗⃗⃗ ∙𝑑𝑟
𝐹
⃗
= ⃗⃗⃗
𝐹 ∙𝑉
( 8)
𝑑𝑡
𝑑𝑡
⃗ − скорость с которой движется точка приложения силы 𝐹
⃗⃗⃗ .
где 𝑉
Средняя за промежуток времени t мощность равна отношению работы A,
совершенной за этот промежуток времени к времени t :
𝐴
⟨𝑃 ⟩ =
(9)
𝑡
В системе СИ мощность измеряется в ваттах,
Вт=
Дж
с
.
§18. Кинетическая энергия тела и ее связь с совершенной над ним работой.
Если на абсолютно твердое тело (материальную точку) действуют
несколько сил и в качестве ⃗⃗⃗
𝐹 взята результирующая всех сил, то работа A
результирующей силы будет равна работе всех сил. Поскольку в этом случае
по второму закону Ньютона
⃗
𝑑𝑉
⃗⃗⃗
𝐹 = 𝑚𝑎
⃗⃗⃗ = 𝑚 𝑑𝑡
, то
𝑉2
𝑉2
⃗
𝑑𝑉
𝑉2
𝑚𝑉22 𝑚𝑉12
⃗⃗⃗⃗
⃗
⃗
𝐴 = ∫𝑚
𝑑𝑟 = ∫ 𝑚 𝑉 𝑑𝑉 = ∫ 𝑚𝑑( ) =
−
𝑑𝑡
2
2
2
𝑉1
Полученное выражение
(10)
𝑉1
𝑚𝑉 2
называется кинетической энергией тела
2
(материальной точки). Из равенства (10) следует, что если работа A
результирующей силы будет больше нуля, то кинетическая энергия
увеличивается, если работа A результирующей силы будет меньше нуля, то
кинетическая энергия уменьшается. Если работа A результирующей силы
равна нулю, то кинетическая энергия не изменяется.
𝑊к =
𝑚𝑉 2
(11)
2
4
Кинетическая энергия механической системы равна сумме кинетических
энергий всех частей системы. Например, для системы, состоящей из n
материальных точек. Она равна:
𝑊к =
𝑚𝑖 𝑉𝑖2
𝑛
∑𝑖=1
2
(12)
⃗ 𝑖 − масса и скорость 𝑖 − той материальной точки.
где 𝑚𝑖 и 𝑉
В соответствии с (10) кинетическая энергия измеряется в джоулях.
Кинетическая энергия механической системы всегда:
− величина аддитивная, скалярная и всегда положительна;
− зависит от выбора системы отсчета.
§19.Консервативные и диссипативные силы. Потенциальная энергия.
Если частица в каждой точке пространства подвержена воздействию других
тел, то говорят, что эта частица находится в поле сил. Так, например, частица
вблизи поверхности Земли находится в поле силы тяжести – в каждой точке
пространства на нее действует сила тяжести 𝐹тяж = 𝑚𝑔 .
Из действующих на тело сил, выделим на два типа :
1) Консервативные силы (например, силы тяжести, упругости, силы
Кулона в электростатике).
Сила называется консервативной, если она зависит только от положения
⃗⃗⃗ = 𝐹
⃗⃗⃗ (𝑟⃗⃗ ), и производимая ею работа при перемещении тела зависит
тела 𝐹
только от начального и конечного положения тела, т.е. не зависит от формы
траектории.
Работа консервативных сил по замкнутой траектории равна нулю.
2) Диссипативные силы ( например, силы трения, сопротивления).
5
Силы, работа которых приводит к диссипации механической энергии тел ,
называются диссипативными (слово «диссипация» означает рассеяние).
В общем случае диссипативными называются силы, всегда направленные
противоположно скоростям тел и, следовательно, вызывающие их
торможение. Диссипативные силы направлены, как правило,
противоположно скорости. Поэтому работа диссипативных сил
A
отрицательна. Рассмотрим случай, когда на тело действуют только
диссипативные силы. Поскольку работа связана с кинетической энергией
соотношением 𝐴
= 𝑊𝑘2 − 𝑊𝑘1 , то работа диссипативных сил всегда
уменьшает кинетическую энергию.
Отметим, что неконсервативные силы не обязательно являются
диссипативными.
Консервативные силы обладают свойством, благодаря которому их
выделили из всех сил. Для поля консервативных сил можно ввести
потенциальную энергию тела 𝑊п так, что разность потенциальной энергии
между начальным и конечным положениями тела равна работе
консервативных сил при перемещении тела из начального положения в
конечное:
𝐴конс = 𝑊п1 − 𝑊п2
(13)
Введенная таким образом потенциальная энергия, зависит только от
положения тела ( взаимного положения тел и его частей).
По определению потенциальной энергии 𝑊п
2
= 𝑊п1 − 𝐴конс .
Начальное положение часто выбирают так, чтобы начальная потенциальная
энергия тела равнялась нулю(нулевой уровень отсчета потенциальной
энергии).Тогда потенциальная энергия тела в некоторой точке поля
потенциальных сил будет равна работе консервативных сил при
перемещении тела из этого положения в положение, где потенциальная
энергия равна нулю. Используя определение работы, можно записать:
(2)
⃗⃗⃗⃗
⃗⃗⃗ конс ∙ 𝑑𝑟
𝑊п2 − 𝑊п1 = ∆𝑊П = − ∫(1) 𝐹
6
(14)
Для силы тяжести ( поле силы тяжести консервативно) при подъеме тела на
высоту h с нулевой высоты изменение потенциальной энергии равно:
ℎ
∆𝑊П = 𝑊п2 − 𝑊п1 = − ∫0 𝑚𝑔 (−𝑑ℎ) = 𝑚𝑔ℎ
(15)
Если на нулевой высоте потенциальная энергия равна нулю,
𝑊п1 = 𝑊П (0) = 0 , то 𝑊п2 = 𝑊П (ℎ) = 𝑚𝑔ℎ −есть потенциальная
энергия тела на высоте ℎ .
Посмотрим, что дает введение потенциальной энергии. Запишем изменение
кинетической энергии тела:
𝑊𝑘2 − 𝑊𝑘1 = 𝐴 = 𝐴конс + 𝐴неконс = 𝑊п1 − 𝑊п2 + 𝐴неконс
(16)
Вычислив отдельно работу неконсервативных и консервативных сил,
действующих на тело, получим, что работа неконсервативных сил равна
изменению суммы кинетической и потенциальной энергии тела.
𝐴неконс = ( 𝑊𝑘2 + 𝑊п2 ) − ( 𝑊𝑘1 + 𝑊п1 )
(17)
Сумма кинетической и потенциальной энергий тела называется его полной
механической энергией 𝑾,
𝑊 = 𝑊𝑘 + 𝑊п
(18)
Тогда равенству (17) можно придать следующую формулировку: изменение
полной механической энергии тела равно работе неконсервативных сил ,
действующих на тело.
Изменение полной механической энергии частицы равно работе всех
действующих на нее неконсервативных сил.
(2)
⃗⃗⃗ неконс ∙ ⃗⃗⃗⃗
∆𝑊 = 𝐴неконс = ∫(1) 𝐹
𝑑𝑟
(19)
В случае равенства нулю работы неконсервативных сил полная
механическая энергия тела остается постоянной.
7
§20.Момент силы относительно точки, относительно оси.
Рис.1
До сих пор при рассмотрении задач динамики мы ограничивались
поступательным движением твердого тела, при котором отрезок,
соединяющий любые две точки абсолютно твердого тела (далее везде будем
назвать тело) в процессе движения остается параллельным себе. При
поступательном движении все точки тела проходят одинаковые пути, имеют
одинаковые скорости, и можно рассматривать движение тела, независимо
от его размера и формы как движение одной точки тела. Все характеристики
поступательного движения ( движения одной точки мы уже введи.
Далее в механике твердого тела будем заниматься вращательным
движением, при котором форма( распределение массы) и размеры имеют
существенное значение.
8
Вращательным движением твердого тела называется движение, при
котором все точки тела двигаются по окружностям, центры которых лежат на
одной и той же прямой, называемой осью вращения. Ось вращения может
находиться вне тела.
При вращательном движении информации о силах, действующих на тело,
недостаточно для характеристики, приводящего к вращению, воздействия.
На результат действия силы влияет также направление силы и точка ее
приложения. Количественной мерой вращательного воздействия является
не сила, а момент силы.
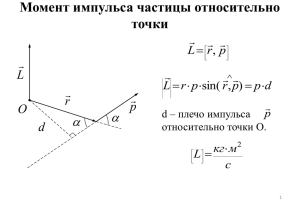
Вектор равный векторному произведению радиус-вектора на силу
называется моментом силы относительно точки О:
⃗⃗ = [𝑟⃗⃗ , ⃗⃗⃗
𝑀
𝐹]
(20)
где 𝑟⃗⃗ –радиус-вектор, проведенный из точки О в точку приложения силы ⃗⃗⃗
𝐹,
⃗⃗ −момент силы относительно точки О.
𝑀
⃗⃗ ⊥ 𝑟⃗⃗ и 𝑀
⃗⃗ ⊥ ⃗⃗⃗
Согласно определению 𝑀
𝐹 , его направление определяется
⃗⃗⃗ по кратчайшему
по правилу правого винта: если рукоятку вращать от 𝑟⃗⃗ к 𝐹
⃗⃗ . Модуль вектора 𝑀
⃗⃗
углу, то направление острия покажет направление 𝑀
равен:
𝑀 = 𝑟𝐹 sin 𝛼
(21)
где 𝛼 − угол между векторами 𝑟
⃗⃗ и ⃗⃗⃗
𝐹.
⃗⃗ ] = Н∙м= Дж.
Размерность [𝑀
⃗⃗ на некоторую ось z, проходящую через точку О,
Проекция вектора 𝑀
⃗⃗ , называется моментом силы
относительно которой определен 𝑀
относительно этой оси:
⃗⃗
𝑀𝑧 = Пр𝑧 𝑀
9
(22)
§21.Момент импульса материальной точки относительно точки,
относительно оси.
Рис.2
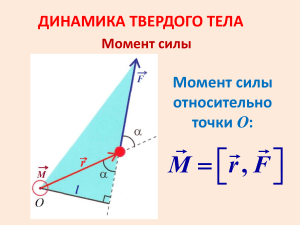
Моментом импульса частицы относительно точки О называется векторное
произведение вектора, соединяющего точку О с частицей и импульса
частицы:
𝐿⃗ = [𝑟⃗⃗ , 𝑝]
(23)
⃗ ⊥ ⃗⃗𝑟 и 𝐿⃗ ⊥ 𝑝
По определению векторного произведения 𝐿
⃗⃗⃗ , его
направление определяется по правилу правого винта: если рукоятку вращать
от 𝑟
⃗⃗ к 𝑝
⃗⃗⃗ по кратчайшему углу, то направление острия покажет
⃗ . Модуль вектора 𝐿⃗ равен:
направление 𝐿
𝐿 = 𝑟𝑝 𝑠𝑖𝑛𝛽
(24)
где 𝛽 − угол между векторами 𝑟
⃗⃗ и 𝑝
⃗⃗⃗ .
10
Размерность [𝐿] =
кгм2
с
= Дж ∙ с.
Заметим, что величина ⃗⃗⃗
𝐿 зависит от выбора точки О, которую, вообще
⃗ проводят из точки О.
говоря, можно выбрать где угодно. Поэтому вектор 𝐿
Если имеется ось вращения, то точку О выбирают на оси.
Проекция вектора ⃗⃗⃗
𝐿 на некоторую ось z, проходящую через точку О,
относительно которой определен ⃗⃗⃗
𝐿 , называется моментом импульса
относительно этой оси:
𝐿𝑧 = Пр𝑧 ⃗⃗⃗
𝐿
(25)
§22.Момент импульса твердого тела относительно неподвижной оси
вращения. Момент инерции.
Рассмотрим вращение тела вокруг закрепленной (неподвижной в
пространстве ) оси. Она . вообще говоря, может не проходить через центр
масс. Инерциальную систему отсчета всегда будем выбирать так, чтобы ось
Оz всегда совпадала с закрепленной осью вращения.
Моментом импульса тела относительно закрепленной оси 𝐿𝑧 , будет сумма
моментов импульса относительно этой оси материальных точек 𝐿𝑖𝑧 , из
которых оно (тело) состоит:
𝐿𝑧 = ∑𝑖 𝐿𝑖𝑧
(26)
Материальная точка с массой 𝑚𝑖 , вращается в плоскости перпендикулярной
оси вращения Оz по окружности радиусом 𝑟𝑖 , с угловой скоростью 𝜔.
Угловая скорость для всех точек тела одинакова. Допустим, вращение
происходит против часовой стрелки. Тогда момент импульса этой
материальной точки относительно оси Оz будет равен:
𝐿𝑖𝑧 = 𝑟𝑖 𝑚𝑖 𝑉𝑖 = 𝑟𝑖 𝑚𝑖 𝜔𝑟𝑖 = 𝜔𝑚𝑖 𝑟𝑖2
⃗ 𝑖 равен 𝜋 ).
(учли, что угол между векторами 𝑟𝑖 и 𝑉
2
11
(27)
С учетом (26),(27) получаем:
𝑁
𝑁
𝐿𝑧 = ∑ 𝜔𝑚𝑖 𝑟𝑖2 = 𝜔 ∑ 𝑚𝑖 𝑟𝑖2
𝑖=1
Величина
(28)
𝑖=1
2
𝐼𝑧 = ∑𝑁
𝑖=1 𝑚𝑖 𝑟𝑖 называется моментом инерции тела
относительно оси Оz .
Момент инерции тела относительно оси Оz (иногда для краткости будем
говорить момент инерции) является скалярной величиной, больше нуля.
Размерность
[𝐼 ] = кг м2 .
Таким образом, момент импульса твердого тела относительно
закрепленной оси можно равнее произведению угловой скорости на
момент инерции тела относительно этой оси:
𝐿𝑧 = 𝐼𝑧 𝜔
(29)
§23.Расчет моментов инерции некоторых твердых тел относительно их
осей симметрии.
В предыдущем параграфе ввели понятие момента инерции твердого тела.
Рассмотрим, как вычислять его для конкретных тел.
Рассмотрим вначале тело произвольной формы и будем исходить из
определения :
2
𝐼𝑧 = ∑𝑁
𝑖=1 𝑚𝑖 𝑟𝑖
(30)
𝑟𝑖 −кратчайшее расстояние от точки до оси.
Переходя к пределу бесконечно большого числа материальных точек
физически бесконечно малого объема, получим:
12
𝐼𝑧 = ∫ 𝑟 2 𝑑𝑚 = ∫ 𝜌𝑟 2 𝑑𝑉
где было учтено, что масса 𝑑𝑚 в малом объеме
𝜌 , соотношением
объему тела.
(31)
𝑑𝑉 , связана с плотностью
𝑑𝑚 = 𝜌𝑑𝑉 .Интегрирование производится по всему
Получим моменты инерции относительно осей симметрии для ряда тел.
1.Полый цилиндр, имеющий массу 𝑚 и радиус r , толщиной стенок которого
можно пренебречь.
Пусть ось z совпадает с осью симметрии цилиндра. Рассчитаем его момент
инерции относительно этой оси с помощью формулы (30). Так как толщиной
стенок цилиндра по условию можно пренебречь, то для всех материальных
точек, из которых он состоит, 𝑟𝑖 = 𝑟 = 𝑐𝑜𝑛𝑠𝑡 , что позволяет вынести 𝑟 за знак
суммирования:
2
2 𝑁
𝐼𝑧 = ∑𝑁
𝑖=1 𝑚𝑖 𝑟𝑖 = 𝑟 ∑𝑖=1 𝑚𝑖
Поскольку
(32)
∑𝑁
𝑖=1 𝑚𝑖 = 𝑚 , где 𝑚 − масса цилиндра, согласно ( )
момент
инерции тонкостенного цилиндра относительно его оси симметрии:
𝐼𝑐 = 𝑚𝑟 2
(33)
Так как кольцо или обруч являются частным случаем тонкостенного
цилиндра, то и для них будет справедлива формула (33).
2.Тонкий однородный стержень.
Однородный стержень вращается вокруг оси ОО₁, перпендикулярной
стержню и проходящей через конец стержня.
13
Рис.3
Выделим элемент dr с массой dm, находящийся на расстоянии r от оси
вращения ОО₁.
Момент инерции выделенного элемента
dI = r²dm = r²ρSdr
(35)
где ρ – плотность стержня, S – площадь поперечного сечения.
Момент инерции всего стержня относительно оси ОО1.
𝐼=
𝑙
∫0 𝑑𝐼
= 𝜌𝑆
𝑙
∫0 𝑟 2 𝑑𝑟
=
𝜌𝑆𝑙 3
3
=
𝑚𝑙 2
3
(36)
3. Момент инерции однородного диска массой m и радиусом R
относительно оси симметрии.
Разбив диск на тонкие круговые полоски и, интегрируя, получим:
2
2
𝑚
𝐼𝐶 = ∫ 𝑟 𝑑𝑚 = ∫ 𝑟 (𝜋𝑅2 ) 2𝜋𝑟𝑑𝑟 =
2𝑚𝑟 4
4𝑅2
(37)
Подставляя пределы интегрирования от 0 до R, окончательно получим:
𝐼𝐶 =
𝑚𝑅2
(38)
2
14
Момент инерции твёрдого тела относительно какой-либо оси зависит
от массы, формы и размеров тела, а также и от положения тела по
отношению к этой оси.
Моменты инерции однородных тел геометрически правильной формы
находятся посредством интегрирования. Для неоднородных тел и тел
неправильной формы моменты инерции определяются экспериментально.
Моменты инерции однородных тел простейшей формы
относительно некоторых осей вращения
Момент
Тело
Положение оси a
Описание
инерции Ic
Материальная точка
массы m
На расстоянии r от точки, ось
неподвижная
𝐼𝐶 = 𝑚𝑟 2
Полый тонкостенный
цилиндр или кольцо
радиуса r и массы m
Ось цилиндра
𝐼𝐶 = 𝑚𝑟 2
Сплошной цилиндр или
диск радиуса r и массы m
Ось цилиндра
𝐼𝐶 = 𝑚𝑟 2
15
1
2
Прямой тонкий стержень
длины l и массы m
Ось перпендикулярна к
стержню и проходит через его
центр масс
Прямой тонкий стержень
длины l и массы m
Ось перпендикулярна к
стержню и проходит через его
конец
𝐼𝐶 = 𝑚𝑙2
Тонкостенная сфера
радиуса r и массы m
Ось проходит через центр
сферы
𝐼𝐶 = 𝑚𝑟 2
Шар радиуса r и массы m
Ось проходит через центр
шара
𝐼𝐶 = 𝑚𝑟 2
𝐼𝐶 =
1
12
𝑚𝑙2
1
3
2
3
2
5
Рис.4
Свяжем момент инерции 𝐼𝑧 относительно произвольной оси Z, с моментом
инерции относительно оси, параллельной данной и проходящей через центр
масс данного тела.
16
Теорема Штейнера (без доказательства).
Момент инерции тела 𝑰𝒛 ,относительно произвольной оси Z, равен сумме
момента инерции этого тела 𝑰𝑪 , относительно оси, проходящей через
центр масс тела параллельно рассматриваемой оси, и произведению
массы тела m на квадрат расстояния между осями.
𝐼𝑧 = 𝐼𝐶 + 𝑚𝑑 2
(39)
где d- расстояние между осями.
§24.Закон сохранения момента импульса.
Пусть на материальную точку (частицу) действуют силы ⃗⃗⃗
𝐹 1 , ⃗⃗⃗
𝐹 2 , … ⃗⃗⃗
𝐹 𝑛.
Равнодействующую всех сил, действующих на материальную точку
.обозначим
⃗⃗⃗
𝐹 равн = ⃗⃗⃗
𝐹 1 + ⃗⃗⃗
𝐹 2 + ⋯ + ⃗⃗⃗
𝐹𝑛
(40)
Ранее мы определили момент импульса материальной точки относительно
точки. Рассмотрим как влияют силы, действующие на материальную точку .
на ее момент импульса. Для этого продифференцируем выражение (23) по
времени:
⃗⃗⃗
𝑑𝐿
𝑑𝑡
𝑑
𝑑𝑟
𝑑𝑝
⃗⃗⃗ 𝑝] + [𝑟 , 𝐹равн ]
= 𝑑𝑡 [𝑟⃗⃗ , 𝑝] = [ 𝑑𝑡 , 𝑝] + [𝑟⃗⃗ , 𝑑𝑡 ] = [𝑉,
(41)
⃗ и импульса 𝑝 совпадают, то [𝑉,
⃗⃗⃗ 𝑝] = 0.
Поскольку направления скорости 𝑉
Поэтому с учетом (40) , (41) и определения момента силы относительно
точки получаем:
⃗⃗⃗
𝑑𝐿
𝑑𝑡
где
⃗⃗ 𝑖
= ∑𝑖 𝑀
⃗⃗ 𝑖 = [𝑟 , 𝐹𝑖 ] − момент 𝑖-ой
𝑀
(42)
силы, действующей на материальную
точку.
17
Производная от момента импульса материальной точки по времени равна
векторной сумме моментов всех действующих на нее сил.
Любую механическую систему можно рассматривать как совокупность
материальных точек. Для простоты будем считать, что она состоит из
взаимодействующих частиц, на которые действуют также внешние силы.
Положение 𝑖 −ой частицы относительно некоторой неподвижной точки О
задается радиус-вектором 𝑟𝑖 .
18
Окончательно получим:
⃗⃗⃗
𝑑𝐿
𝑑𝑡
⃗⃗ 𝑖,внеш
= ∑𝑖 𝑀
(43)
В отличие от формулы (42) , 𝐿
⃗ – векторная сумма моментов импульсов всех
материальных импульсов, входящих в рассматриваемую систему.
В соответствии с этим уравнением производная момента импульса
механической системы по времени равна векторной сумме моментов всех
действующих на нее внешних сил.
⃗⃗⃗
𝑑𝐿
=0 , то есть ,что вектор
𝑑𝑡
момента импульса механической системы не меняется с течением времени.
Это утверждение составляет закон сохранения момента импульса :
⃗⃗ 𝑖,внеш =0, то из (43) следует, что
Если ∑𝑖 𝑀
Момент импульса механической системы сохраняется , если векторная
сумма моментов всех внешних с.действующих на систему, равна нулю.
Данное утверждение является формулировкой закона сохранения момента
импульса в механике Ньютона.
19
Этот закон имеет и другую формулировку. Которая будучи менее общей,
применима за рамками механики Ньютона, например , в микромире:
момент импульса замкнутой системы сохраняется.
Спроектировав все величины, входящие в уравнение (43), на некоторое
направление
z , получим:
𝑑𝐿𝑧
𝑑𝑡
= ∑𝑖 𝑀𝑧𝑖,внеш
(44)
Согласно равенству (44) производная по времени от момента импульса
системы относительно оси z равна сумме моментов внешних сил
относительно этой оси. Из этого равенства следует, что когда сумма внешних
сил относительно некоторой оси равна нулю, момент импульса системы
относительно этой оси остается постоянным.
20