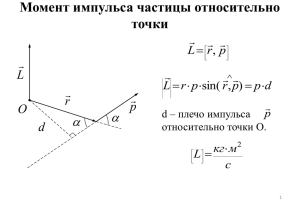
Механика 1 курс, 2 семестр. Содержание 1. 2. Кинематика материальной точки Кинематика вращательного движения твердого тела вокруг неподвижной оси 3. Динамика. Инерциальные системы отсчета 4. Классификация сил в природе 5. Неинерциальные системы отсчета. Силы инерции 6. Импульс системы материальных точек. Закон сохранения импульса. 7. Работа и мощность силы 8. Кинетическая и потенциальная энергия материальной точки 9. Закон сохранения полной механической энергии системы 10. Момент импульса частицы и момент силы 11. Момент инерции твердого тела относительно неподвижной оси 12. Уравнение вращения твердого тела вокруг неподвижной оси Кинематика материальной точки. Системы координат Положение частицы в пространстве при векторном способе описания движения задается радиусом-вектором r, проведенным из начала координат к частице. r r ( x, y , z , t ) r x (t ) i y ( t ) j z ( t ) k Траектория – линия, которую описывает точка при своем движении (геометрическое место точек-концов радиуса-вектора частицы). Перемещением за промежуток времени Δt называется вектор, проведенный из начального в конечное положение частицы (из точки 1 в точку 2). r r2 (t t ) r1 (t ) Вектор средней скорости V за промежуток времени Δt равен Мгновенная скорость V частицы Вектор мгновенной скорости V направлен по касательной к траектории в сторону движения частицы. Модуль V скорости частицы равен Ускорением называется вектор а, равный производной по времени вектора скорости V частицы: Модуль а ускорения равен Модуль ускорения, вообще говоря, не совпадает с производной по времени dV/dt модуля скорости частицы. Если зависимость радиуса-вектора частицы от времени известна, то можно решить так называемую прямую задачу кинематики – определить скорость и ускорение частицы в каждый момент времени. 2 dr (t ) d r (t ) v (t ) ; a (t ) dt dt 2 Обратная задача кинематики состоит в том, чтобы зная зависимость от времени ускорения частицы а(t) и начальные условия движения (скорость V0 и ускорение а0 в начальный момент времени t = 0), определить в каждый момент времени скорость V(t) и положение частицы в пространстве r(t). Пример. Частица стартует с начальной скоростью V0 из точки, заданной радиусом-вектором r0. Задача состоит в том, чтобы, зная ускорение частицы a, которое постоянно, определить V(t) и r(t). Этому условию отвечает, например, движение камня брошенного под углом к горизонту и двигающегося далее с постоянным ускорением a = g. По определению ускорения Интегрируя это уравнение, найдем скорость V: По определению скорости В проекциях на декартовы оси координат X,Y эти векторные соотношения имеют вид: 2 axt Vx (t ) V0 x a x t; x(t ) x0 V0 x t ; 2 a yt 2 Vy (t ) V0 y a y t; y (t ) y0 V0 y t 2 В случае камня, брошенного под углом α0 к горизонту: V0 x V0 x cos 0 ; V0 y V0 y sin 0 ; ax 0; a y g Путь. Пусть частица, двигаясь вдоль некоторой траектории, переместилась из точки 1 в точку 2. Путь равен измеренному вдоль траектории расстоянию, пройденному частицей в процессе движения (длина траектории). Обычно путь обозначают буквой S или символом ΔS. Установим связь между модулем скорости V частицы и путем S. Следовательно, модуль скорости равен производной пути по времени. Пройденный частицей путь: Ускорение при криволинейном движении Рассмотрим участок 1-2 криволинейной траектории. В математическом анализе строго доказывается, что если точку 2 устремить к точке 1, участок 1-2 траектории R по своей форме будет сколь угодно мало отличается от дуги окружности некоторого радиуса, который называется радиусом кривизны траектории в точке 1. Центр этой окружности называется центром кривизны траектории в точке 1. Единичный вектор n, перпендикулярный касательной к траектории и направленный к центру кривизны, называется вектором нормали к траектории. Представим вектор скорости в виде произведения модуля скорости на единичный вектор, совпадающий по направлению с направлением скорости тела v/v = τ (тангенциальный вектор): V = Vτ Тогда ускорение можно записать так dS dα d d dt dS d ; R 1 dS V 1 R dt R n 1 d n dV V 2 a n a a n dt R Модуль полного ускорения можно найти по формуле: 2 4 dV V a a a2 a 2n 2 dt R a a n g v v 2x v 2y an g cos g ( v x v ) a g cos(90 ) g sin g ( v y v ) Кинематика вращательного движения твердого тела вокруг неподвижной оси Твердым (или абсолютно твердым) телом в механике называется тело, при движении которого расстояния между любыми двумя его точками остаются неизменными. При поступательном движении любая прямая, жестко связанная с движущимся телом, остается параллельной своему начальному положению. Вращением вокруг неподвижной оси называется движение, при котором существуют по крайней мере две неподвижные точки тела. Прямая, проходящая через эти точки, называется осью вращения. Можно показать, что все лежащие на оси вращения точки тела неподвижны. Любая другая точка тела движется в перпендикулярной к оси вращения плоскости по окружности с центром на оси вращения, соответственно, скорость этой точки перпендикулярна к оси вращения и направлена по касательной к окружности. При поступательном движении все точки твердого тела движутся по одинаковым траекториям и в каждый момент времени имеют одинаковые скорости и ускорения. Вращательное движение Точка А – произвольная точка тела с осью вращения z. Угловой координатой (углом поворота) называется угол между положительным направлением оси х и проекцией радиусавектора r на координатную плоскость ху. Вектором элементарного поворота d называется вектор, модуль которого равен модулю угла поворота d : | d | = d . Вектор d направлен вдоль оси вращения тела, его направление определяется правилом правого винта. Угловой скоростью тела называется вектор: d dt Вектор угловой скорости совпадает по направлению с вектором d и, следовательно, направлен вдоль оси вращения тела. Если ось z неподвижной декартовой системы координат совпадает с осью вращения тела, проекция на ось z вектора угловой скорости равна d z dt Модуль угловой скорости d dt численно равен углу поворота тела за единицу времени. Угловое ускорение d dt Направление вектора совпадает с направлением вектора d приращения угловой скорости за бесконечно малый промежуток времени dt. Если тело вращается вокруг неподвижной оси OO', то вектор d, и, следовательно, вектор лежат на оси вращения. Если ось z неподвижной декартовой системы координат направлена вдоль оси вращения тела, то dz z dt Векторы d , и не имеют определенных точек приложения и могут откладываться из любой точки неподвижной оси вращения. При равномерном вращении d const dt следовательно t Равномерное вращение можно характеризовать периодом вращения Т – временем, за которое точка совершает один полный оборот φ = 2π =ωТ: T 2 Частота вращения — число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени: n 1 T n Герц При равноускоренном вращательном движении ε const (t ) 0 t; (t ) 0 0 t t2 2 ; S (t ) R ; dV d ( R ) d V2 2 a R R; an R dt dt dt R Связь между линейными и угловыми кинематическими величинами Рассмотрим произвольную точку в твердом теле, которое вращается вокруг закрепленной оси. Найдем связь линейной скорости и ускорения произвольной точки А тела с угловой скоростью и угловым ускорением. R dr R d r sin d В векторном виде dr d , r Разделим это равенство на dt dr d , r или dt dt v , r Величины линейной и угловых скоростей связаны соотношением v v r sin R где R - расстояние от выделенной точки до оси вращения. dv d dr a , r , , r , v a an dt dt dt a r sin R 2 v an v 2 R R Динамика. Инерциальные системы отсчета Динамика изучает движение тел в связи с вызывающими его причинами – взаимодействиями тел. В основе динамики лежат законы, сформулированные Ньютоном в 1687 году. I закон Ньютона (закон инерции). В качестве первого закона движения Ньютон принял закон инерции, открытый Галилеем: тело (материальная точка), не подверженное внешним воздействиям, находится в состоянии покоя, либо движется прямолинейно и равномерно с этим все системы отсчета делятся на два класса: в одном закон. Закон инерции не может быть справедлив во всех системах отсчета: если закон инерции справедлив в некоторой системе отсчета, то в любой системе, движущейся ускоренно относительно первой, он не действует. Современная формулировка I закона Ньютона: существует система отсчета, называемая инерциальной, в которой не подверженное внешним воздействиям тело находится в состоянии покоя, либо движется равномерно и прямолинейно. Первый закон Ньютона фактически дает определение инерциальной системы отсчета. Любая другая система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной, также является инерциальной. Неинерциальной системой отсчета называется всякая система, движущаяся ускоренно по отношению к инерциальной системе отсчета. В неинерциальной системе отсчета свободное тело движется ускоренно. Принцип относительности Галилея. Согласно принципу относительности, сформулированному Галилеем, все инерциальные системы отсчета по своим механическим свойствам эквивалентны друг другу. Во всех инерциальных системах отсчета свойства пространства и времени одинаковы, а законы механики имеют одинаковую математическую форму выражения. Никакими механическими опытами, проводимыми в какой-либо инерциальной системе отсчета, нельзя установить, покоится данная система или движется равномерно и прямолинейно. Поскольку движение относительно, траектория материальной точки, ее скорость зависят от выбора системы отсчета. В то же время законы классической механики во всех инерциальных системах отсчета записываются одинаково. Преобразования Галилея. Преобразования Галилея - это формулы преобразования координат материальной точки и времени при переходе от одной инерциальной системы отсчета к другой, двигающейся относительно первой прямолинейно со скоростью u = const. r0 ut , r r0 r r ut x x' ux t , y y' u y t , z z' uz t , t t ; v v'u a a ' Время и размеры тел по Галилею одинаковы во всех системах отсчета. При замене координат движущихся материальных точек и времени с помощью соотношений Галилея уравнения механики не меняются по форме. (они инвариантны по отношению к преобразованиям Галилея). Преобразования Галилея являются математическим отражением принципа относительности Галилея. Второй и третий законы Ньютона Сила – векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел. Принцип суперпозиции сил. Пусть материальная точка взаимодействует с несколькими телами (телом 1, телом 2 и т.д.). Опыт показывает, что действующую на материальную точку силу F можно представить как векторную сумму нескольких сил: F = F1 + F2 + ... + Fi + ..., где Fi — сила, с которой действует на материальную точку тело с номером i в отсутствие других тел. Это равенство выражает принцип суперпозиции действующих на материальную точку сил. Масса. Опыт показывает, что всякое тело оказывает сопротивление при любых попытках изменить его скорость – как по модулю, так и по направлению. Это свойство, выражающее степень неподатливости тела к изменению его скорости, называют инертностью. У различных тел оно проявляется в разной степени. Мерой инертности служит величина, называемая массой. Отношение масс двух различных тел обратно отношению ускорений, сообщаемых им равными силами: m1 m2 a2 a1 Таким образом, сравнение масс двух тел, на которые действует одна и та же сила, сводится к сравнению ускорений этих тел. Единицей массы в СИ является масса эталонного образца - килограмма (кг). ́ Импульс (количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс материальной точки равен произведению массы m этого тела на его скорость v: p mv Второй закон Ньютона: В инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку. dp d mv Fi F dt dt i При m = const : 2 d mv dv d r m ma m 2 Fi F dt dt dt i ma F - основное уравнение динамики. Вектор Fdt называется импульсом силы за время dt. Изменение импульса тела за время dt равно импульсу тела: dp = Fdt . Третий закон Ньютона: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: 1 F12 2 F21 F12 F21 Таким образом, силы взаимодействия появляются парами. Они приложены к разным материальным точкам. Классификация сил в природе Все силы, известные науке в настоящее время, в конечном счете сводятся к четырем типам фундаментальных взаимодействий — гравитационным, электромагнитным, ядерным и слабым. Ядерные и слабые взаимодействия характерны для процессов с участием атомных ядер и элементарных частиц и проявляются на малых расстояниях (~ 10–13 см). Электромагнитные и гравитационные силы убывают с увеличением расстояния между взаимодействующими телами гораздо медленнее. Сила гравитационного притяжения. Согласно открытому Ньютоном закону всемирного тяготения две материальные точки притягиваются с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними: Здесь γ = 6,672 10–11 м3/(кг с2) – гравитационная постоянная. Сила Fгp – сила гравитационного притяжения, гравитационная сила, сила тяготения. Гравитационную силу F21, действующую на тело массой m2 со стороны тела массой m1, можно записать в векторной форме: где er — единичный вектор, направленный от тела 1 к телу 2. Вблизи поверхности Земли тело массой m притягивается к Земле с силой: mM З MЗ Fпр m 2 mg 2 RЗ RЗ Весом тела называется сила, с которой тело вследствие тяготения к Земле действует на опору или натягивает нить подвеса. Сила тяжести действует всегда, а вес проявляется лишь тогда, когда на тело кроме силы тяжести действуют другие силы. Вес тела равен силе тяжести только в том случае, когда ускорение тела относительно земли равно нулю. В противном случае вес Р = m(g-a), где a — ускорение тела с опорой относительно Земли. Если тело свободно движется в поле силы тяготения, то a = g и вес равен нулю, т.е. тело будет невесомым. Невесомость — это состояние тела, при котором оно движется только под действием силы тяжести. Силы упругости возникают в результате взаимодействия тел, сопровождающегося их деформацией. Упругая сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия (закон Гука): Fупр k r или в проекции на ось x: Fупр x k x где Δr или Δх – смещение точки приложения силы относительно положения равновесия, k – коэффициент упругости (или жесткости). Кулоновская сила. Согласно закону Кулона сила взаимодействия между двумя заряженными телами (материальными точками) равна: где q1,q2 — модули зарядов, r — расстояние между телами, ε0 = 0,88510–11 Ф/м – электрическая постоянная. Сила трения скольжения возникает при скольжении данного тела по поверхности другого: Fтр.ск N где μ — коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей; N — сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную направлению движения данного тела относительно другого. Сила трения качения возникает при качении тел цилиндрической или шарообразной формы по гладкой поверхности вследствие деформации соприкасающихся тел. На гладкой поверхности в месте ее соприкосновения с телом круглой формы появляются углубление и и бугорок. Вследствие этого возникает сила сопротивления движению F (сила реакции), горизонтальная составляющая которой называется силой трения качения, а вертикальная составляющая - силой нормальной реакции опоры N . Обычно величина силы трения качения во много раз меньше силы трения скольжения. Неинерциальные системы отсчета. Силы инерции Основное уравнение динамики справедливо только в инерциальных системах отсчета. Как следует изменить основное уравнение динамики, чтобы оно оказалось справедливым и для неинерциальных систем отсчета? Поступательная сила инерции Пусть имеются две системы отсчета: неподвижная К и К' (поезд), движущаяся поступательно относительно К со скоростью v0 и ускорением а0 (поезд). Пусть некая частица в поезде движется относительно поезда со скоростью v' и ускорением а'. r r 'r0 v v' v 0 Для неинерциальной системы отсчета: a a 'a0 ma ma ma0 F ma0 F Fин Fин ma0 поступательная сила инерции Это и есть основное уравнение динамики в неинерциальной системе отсчета, перемещающейся поступательно с ускорением а0. Из него видно, что даже при F = 0 частица будет двигаться в неинерциальной системе с ускорением, в общем случае отличным от нуля, причем так, как если бы на нее действовали некоторая сила Fин. Эти силы назвали силами инерции. Введение сил инерции позволяет формально сохранить основное уравнение динамики и для неинерциальных систем: слева — произведение массы частицы на ее ускорение (но уже в неинерциальной системе отсчета), справа — силы. Однако кроме силы F, обусловленной действием окружающих тел (силы взаимодействия), необходимо учесть и силу инерции Fин = – ma0. П р и м е р. Вагон движется с ускорением a0 по прямолинейному горизонтальному участку дороги. К потолку вагона на нити подвешен груз массой т. Найти угол отклонения нити от вертикали. Решить задачу в системе отсчета, связанной с вагоном. В вагоне груз покоится a' = 0. ma ' F ma0 T mg ma0 0 Силы инерции при вращательном движении Система К' (карусель) вращается относительно системы К с постоянной угловой скоростью ω = const вокруг неподвижной в системе К оси z. Совместим начала отсчета обеих систем, чтобы в некоторый момент времени t радиус-векторы r и r' частицы в них совпали. Если частица в К' покоится, то ее перемещение в К системе за время dt обусловлено только поворотом r вместе с К' на угол dφ. Если она движется, то совершит дополнительное перемещение v'dt. Суммарным перемещением в системе К будет: Разделив это выражение на dt, получим закон преобразования скоростей: Найдем теперь связь ускорений в обеих системах. Приращение скорости при ω = const. Найдем dv'. Если частица движется в К' системе c v' = const, то приращение вектора v' в К-системе обусловлено только его поворотом на угол dφ (вместе с К'-системой) и равно, как и в случае с r, векторному произведению [dφ, v']. Если же частица имеет ускорение а' в К'-системе, то за время dt вектор v' получит еще дополнительное приращение a'dt: Поставив это соотношение в выражение для dv, получим: Откуда Третье слагаемое в правой части направлено по радиусу к оси вращения и поэтому называется центростремительным или осестремительным ускорением. Второе слагаемое называется кариолисовым ускорением Отсюда произведение ma': 2 ma ' ma ma0 2mv, m R F Fин Fкор Fцб v' = 0 П р и м е р. При точном решении задач о движении тел относительно земной поверхности нужно учитывать центробежную силу инерции, модуль которой равен: Fцб = тω2R = тω2RЗcosφ. Здесь ω - угловая скорость вращения Земли вокруг собственной оси; φ - широта местности на поверхности Земли, где расположено тело массой т, RЗ - радиус Земли. Центробежная сила инерции направлена перпендикулярно оси вращения Земли. На расположенное вблизи поверхности Земли тело массой т, скорость которого по отношению к Земле равна нулю, действует центробежная сила инерции и сила гравитационного притяжения, направленная к центру Земли и равная по модулю Везде, кроме экватора и полюса, благодаря наличию центробежной силы вектор g не направлен к центру Земли. R П р и м е р. Поезд массой т движется со скоростью V вдоль меридиана в направлении с севера на юг. Широта местности φ. Найдем силу бокового давления, с которой поезд действует на рельсы. Сила бокового давления возникает за счет действия на поезд силы Кориолиса, величина которой равна Сила бокового давления со стороны рельс уравновешивает силу Кориолиса. Особенности сил инерции: 1. Силы инерции обусловлены не взаимодействием тел, а свойствами самих неинерциальных систем отсчета. Поэтому на силы инерции третий закон Ньютона не распространяется. 2. Эти силы существуют только в неинерциальных системах отсчета. В инерциальных системах отсчета сил инерции нет, и понятие "сила" в этих системах отсчета применяется только в ньютоновском смысле, как мера взаимодействия тел. 3. Все силы инерции, подобно силам тяготения, пропорциональны массе тела. Импульс системы материальных точек. Закон сохранения импульса. Газообразное, жидкое, твердое тело можно разбить на столь малые участки с массами mi, что их размерами можно пренебречь, т.е. рассматривать как систему материальных точек. Тела, входящие в систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. мы Силы, с которыми на данное тело воздействуют остальные тела системы, будем называть внутренними. Силы, обусловленные воздействием тел, не принадлежащих системе, будем называть внешними. В случае, если внешние силы отсутствуют, система называется замкнутой. Импульсом системы P называется векторная сумма импульсов тел, образующих систему. Найдем изменение полного импульса системы. i 1,2,..., N i 1,2,..., N N dpi d N dP pi Fi Fij Fi dt i 1 dt i 1 dt i i j i i dP Fi Fвнеш dt i t2 P2 P1 P Fвнеш dt t1 Если система замкнута Fвнеш = 0: dP Fвнеш 0 P const dt - закон сохранения импульса. Если импульс внешней силы Fвнеш Δt 0: P const Аналогично, если Fвнеш_x 0: Px const Назовем центром масс (центром инерции) системы точку, положение которой в пространстве задается радиусом-вектором rc, определяемым следующим образом: m1r1 m2 r2 ...mN rN rc m1 m2 ...mN mi ri i m i i mi ri i m Скорость центра инерции dri mi ri mi drc d i dt i vc dt dt mi m i mi vi i m pi P i m m P mv c - импульс системы тел равен произведению массы системы на скорость ее центра масс. Для замкнутой системы P = const и ее центр масс либо движется прямолинейно и равномерно (vc = const), либо остается неподвижным. dP d dv c mv c m mac Fi Fвнеш dt dt dt - закон движения центра масс: центр масс системы частиц движется как материальная точка, в которой заключена масса всей системы, и к которой приложены сила, равная сумме всех внешних сил. Работа и мощность силы Элементарной работой силы F(r,t) называется скалярное произведение: 2 A F dr A F dr cos F ds cos 1 Работа силы F на конечном пути 1-2 равна: A12 F dr , 2 1 где Fdr – интеграл от векторной функции F вдоль траектории движения между точками 1 и 2. Формула A F dr l справедлива не только для частицы, но и вообще для любого тела (или системы тел), если под dr (или ds) понимать перемещение точки приложения силы F. Если F F1 F2 2 2 2 A F dr F1 F2 dr F1 dr F2 dr A1 A2 2 1 1 1 A Н м Дж 1 Мощность – это физическая величина, которая характеризует работу силы за единицу времени. Мгновенной мощностью силы F называется величина, равная A Fdr N Fv dt dt A Fdr Ndt t2 A F dr N dt 2 1 t1 Дж N Вт с Консервативные и диссипативные силы. Консервативные силы (потенциальные силы) – это силы, работа которых не зависит от формы траектории (зависит только от положений начальной и конечной точек приложения сил). Силы, работа которых зависит от формы траектории являются неконсервативными. К ним, в частности, относятся диссипативные силы – это силы трения и сопротивления. Любая диссипативная сила может быть представлена в виде: F= – k(v)v где v — скорость данного тела относительно другого тела (или среды), с которым оно взаимодействует; k(v) – положительный коэффициент. Диссипативная сила F всегда направлена противоположно вектору v. Суммарная работа всех внутренних диссипативных сил в системе – величина всегда отрицательная независимо от системы отсчета. Примеры консервативных сил Работа силы тяжести. 2 A A F dr mg dr 2 2 1 1 1 g g (0,0, g ), dr dr (dx, dy, dz) A mg dr mgdz Поскольку A зависит только от z, вычисление интеграла по криволинейной траектории сводится к интегрированию по z: 2 2 2 1 1 1 A A mg dr mg dz mg ( z1 z2 ) – работа однородной силы тяжести не зависит от формы траектории движения частицы, а определяется только разностью ее координат z в начальном и конечном положении. Работа гравитационной силы в общем случае. Пусть в точке О находится материальная точка массы М, которая действует гравитационной силой Fгp на частицу А массы m: m 2 mM A Fгр dr 2 er dr r 1 1 2 М mM mM mM A Fгр dr 2 er dr 2 er dr cos 2 dr, r r r где er dr cos dr cos dr приращение модуля радиуса-вектора r частицы. Элементарная работа А зависит только от расстояния r между точечными массами. Вычисление криволинейного интеграла сводится к обычному интегрированию по r: r2 1 1 mM A A Fгр dr 2 dr mM r r2 r1 1 1 r1 2 2 Работа гравитационной силы не зависит от формы траектории, а определяется только начальным и конечным положением частицы, а именно, расстояниями r1 и r2 до силового центра. Работа упругой силы. Один конец пружины с жесткостью k закреплен неподвижно, а другой может переметаться горизонтально под действием внешней силы. kr Fупр kr Пусть под действием внешней силы свободный конец пружины переместится из точки x1 в точку x2. Работа упругой силы в ходе этого перемещения будет равна: A Fупр dr kr dr kxdx, x2 2 k 2 A A Fупр dr kr dr kxdx x1 x22 2 1 1 1 x1 2 2 – работа упругой силы на конечном пути зависит только от положения начальной х1 и конечной х2 координат точки ее приложения. Работа силы трения. N Fтр kN mg mg A Fтр dr Fтр dr cos 180 mgds, dr ds ds – элементарный путь. Элементарная работа А зависит только от переменной s — пути бруска, вычисление интеграла по криволинейной траектории сводится к интегрированию переменной s. Работа силы трения на пути бруска из точки 1 в точку 2 равна: по 2 2 A A Fтр dr mgds mg ds mgS, 2 2 1 1 1 1 где S — пройденный путь. В отличие от работы силы тяжести, гравитационной, кулоновской и упругой сил, работа силы трения зависит от длины пройденного телом пути S, и, следовательно, от формы траектории. Кинетическая энергия материальной точки Кинетической энергией частицы называется величина: mv 2 Т 2 Кинетическая энергия системы частиц mi v i2 Т 2 i Теорема о кинетической энергии: Работа равнодействующей всех приложенных к частице сил равна приращению кинетической энергии частицы. Утверждение справедливо как для элементарной работы: d (mv ) dr 1 A Fdr dr m dv mvdv md ( v v) dt dt 2 2 1 m v 2 md ( v ) d dT , 2 2 так и для работы на конечном пути: mv 2 mv 22 mv12 A A dT d T2 T1 T 2 2 2 1 1 v1 2 2 v2 Потенциальная энергия частицы в силовом поле Силовое поле. Если на частицу в каждой точке пространства действует определенная сила, то всю совокупность сил называют силовым полем. Если силы не зависят от времени, силовое поле называется стационарным. Консервативным называется поле, в котором совершаемая при перемещении частицы из произвольного начального в произвольное конечное положение работа сил поля не зависит от формы траектории и характера движения, а определяется только начальным и конечным положением частицы. Силы консервативного поля — консервативные силы. Работа консервативных сил на замкнутой траектории равна нулю. Доказательство: A1a 2b1 A1a 2 A2b1 A2b1 F (dr ) Fdr A1b2 A1b2 Fdr A2b1 A1b2 В силу консервативности поля A1a 2 A1b2 и A1a 2b1 A1a 2 A2b1 A1a 2 A1b2 0 Пусть имеется консервативное силовое поле. Частица расположена в точке Р поля с координатами x, у, z. Выберем произвольную точку О (x0, у0, z0) поля и назовем ее началом отсчета потенциальной энергии: в точке О потенциальная энергия частицы равна нулю. Потенциальной энергией U частицы в точке Р консервативного поля называется работа сил поля, совершаемая при перемещении частицы из данной точки Р в точку О, принятую за начало отсчета потенциальной энергии: U Fdr O P В силу свойств консервативного поля интеграл не зависит от формы траектории и характера движения частицы, а определяется только положением точек Р и О в пространстве. Свойства потенциальной энергии. 1. Потенциальная энергия является функцией только координат x, у, z. 2. Работа А12 сил поля при перемещении частицы из произвольного начального в произвольное конечное положение равна убыли потенциальной энергии частицы: A12 U1 U 2 A12 A1O 2 A1O 2 A1O AO 2 A1O A2O (U 0) U1 U 2 3. Потенциальная энергия частицы определена с точностью до произвольной постоянной величины. Для вычисления потенциальной энергии частицы в консервативном силовом поле необходимо: 1) выбрать положение начала отсчета потенциальной энергии (точка О); 2) вычислить работу сил поля, совершаемую при перемещении частицы по произвольной траектории из точки Р поля в точку О. Полученная величина равна потенциальной энергии частицы в точке Р поля. Потенциальная энергия в однородном поле силы тяжести О (x0,y0, z0) О (0,0, 0) U APO mg( z z0 ) mgz В качестве начала отсчета потенциальной энергии в однородном поле силы тяжести можно рассматривать любую точку плоскости z0 = 0. Потенциальная энергия тела в гравитационном поле. U APO 1 1 mM mM r rO rP Потенциальная энергия тела в поле упругой силы. U APO 2 k 2 kx xP xO2 2 2 Потенциальная энергия системы частиц U: Пусть в замкнутой системе частиц действуют только консервативные силы. Зафиксируем произвольное положение частиц системы (состояние О) и примем это состояние за состояние с нулевой потенциальной энергией. Пусть система перешла в другое произвольном состояние Р с другим набором координат частиц. Потенциальной энергией системы частиц в положении Р называется работа всех консервативных сил, совершаемая при переходе системы из состояния Р в состояние О: где Fi – равнодействующая всех приложенных к i-той частице сил. 1 1 N U U1 U 2 ... U N Ui , 2 2 i 1 где U — потенциальная энергия системы; Ui – потенциальная энергия i-той частицы в силовом поле всех остальных частиц системы. Связь потенциальной энергии и силы поля. Если в консервативном силовом поле сила потенциальная энергия частицы также известна: F(r) известна, U ( x, y, z ) Fdr O P Решим обратную задачу. Пусть задана потенциальная энергия U(x,y,z). Нужно определить силу, действующую на частицу в каждой точке пространства. A Fdr dU – работа консервативной силы равна убыли потенциальной энергии. По свойствам скалярного произведения: Fdr Fx dx Fy dy Fz dz dU ( x, y, z ) U ( x, y, z ) U ( x, y, z ) U ( x, y, z ) dU ( x, y, z ) dx dy dz x y z dU ( x, y, z ) Fx dx Fy dy Fz dz Сравнение дает: U ( x, y, z ) U ( x, y, z ) U ( x, y, z ) Fx , Fy , Fz x y z Или в векторном виде: U ( x, y, z ) U ( x, y, z ) U ( x, y, z ) F ex ey ez x y z Градиентом скалярной функции U(x,y,z) называется векторная функция: U U U grad U ex ey ez x y z Градиент функции U можно представить в виде произведения векторного оператора набла на саму функцию: ex ey ez x y z grad U U Таким образом F grad U U Закон сохранения полной механической энергии частицы ёПусть частица находится в консервативном силовом поле, ее скорость v, потенциальная энергия задана функцией U(x,y,z). Полной механической энергией Е частицы называется сумма ее кинетической Т и потенциальной U энергий: mv 2 E T U U ( x, y , z ) 2 Закон сохранения полной механической энергии частицы: Если на частицу действуют только консервативные силы, ее полная механическая энергия с течением времени сохраняется: E T U const Доказательство. Пусть частица переместилось из произвольного положения 1 в произвольное конечное положение 2. начального Согласно теореме о кинетической энергии работа А12 сил поля равна приращению кинетической энергии частицы: A12 T2 T1 В процессе перемещения на частицу действуют только консервативные силы, работа которых равна убыли потенциальной энергии: A12 U1 U 2 T2 T1 U1 U2 T1 U1 T2 U2 Пусть на частицу помимо консервативных сил действуют неконсервативные диссипативные силы. Согласно теореме о кинетической энергии работа ВСЕХ приложенных к частице сил при ее перемещении из начального в конечное положения равна приращению кинетической энергии: A12 T2 T1 (1) A12 A12конс A12дисс (2) A12конс U1 U2 (3) A12 U1 U2 A12дисс (4) Приравняв (1) и (4), получим: U1 U2 A12дисс T2 T1 A12дисс T2 U2 T1 U1 E2 E1 – работа диссипативных сил при перемещении частицы из произвольного начального положения в произвольное конечное положение равна приращению полной механической энергии частицы. Закон изменения полной механической энергии системы Пусть на тела системы действуют внутренние консервативные силы, внешние консервативные силы, а также диссипативные силы (силы трения и сопротивления среды), как внутренние, так и внешние. Отнесем к сторонним силам все внешние консервативные силы и все диссипативные силы. Пусть Aстор – полная работа сторонних сил, совершаемая над телами системы. Работа сторонних сил Астор при переходе системы частиц из произвольного начального в произвольное конечное положение равна приращению полной механической энергии системы: Aстор E2 E1 где Е1, Е2 – полная механическая энергия системы в начальном и конечном положениях. Момент импульса частицы и момент силы Пусть частица массы m движется со скоростью v. Положение частицы в пространстве задается радиусом-вектором r, проведенным из некоторой неподвижной точки О (не обязательно совпадающей с началом неподвижной системы координат с осями x, у, z). Моментом импульса частицы относительно неподвижной точки О называется вектор L, равный: L r , p где р = mv – импульс частицы. L L rp sin l p p m где 1р - кратчайшее расстояние от точки О до линии, вдоль которой направлен вектор импульса. Расстояние 1р называется плечом импульса. Вектор L перпендикулярен плоскости, в которой лежат векторы r и р. Моментом импульса Lz частицы относительно неподвижной оси z называется проекция на эту ось момента импульса L частицы, вычисленного относительно произвольной точки О оси z. Момент импульса Lz относительно оси, является скалярной величиной в отличие от момента импульса L относительно точки. Моментом силы F относительно неподвижной точки О называется вектор, равный: M r, F M M rF sin lF F где lF – кратчайшее расстояние от точки О до линии действия силы F. Расстояние lF называется плечом силы. Моментом силы Mz относительно неподвижной оси z называется проекция на эту ось вектора М момента силы, рассчитанного относительно произвольной точки О оси z. Момент силы Mz относительно оси является скалярной величиной. Уравнение моментов Найдем производную по времени момента импульса L частицы относительно неподвижной точки О: L r , p dL dr dp , p r , v, p r , F dt dt dt dL r, F M dt – уравнение моментов. v p Из уравнения моментов следует закон сохранения момента импульса частицы: если момент М действующих на частицу сил относительно неподвижной точки пространства равен нулю, момент импульса L частицы относительно этой точки сохраняется. dL M 0 L const dt Закон сохранения момента импульса системы частиц Рассмотрим систему частиц, импульсы которых в некоторой системе отсчета равны p1, p2, ..., pi, … i – номер частицы. Положения частиц в пространстве задаются радиусами-векторами r1, r2, ..., ri, …, проведенными из некоторой неподвижной точки О. Моментом импульса L системы частиц относительно неподвижной точки О называется векторная сумма моментов импульса Li всех частиц системы относительно той же точки: L ri , pi Li i i Продифференцируем обе части равенства по времени: dL dLi Mi dt dt i i M i M i внутр M i внеш i i Выберем любые две частицы 1 и 2: M1 M 2 r1 , F2 r2 r1 , F2 r1 , F1 r2 , F2 r2 , F2 0 ( F1 F2 ) i Поскольку все внутренние силы – это силы попарного взаимодействия частиц системы друг с другом: M i внутр 0 i dL M i внеш M внеш dt i – уравнение моментов для системы частиц. Закон сохранения момента импульса системы частиц: Момент импульса L замкнутой ( Mвнеш = 0 ) системы частиц с течением времени сохраняется. dL M внеш 0 L const dt Момент импульса L незамкнутой системы частиц или его проекция на некоторую ось могут сохраняться, если: M i внеш 0, но M i внеш i dL 0 M i внеш 0 L const dt i 2) Если проекция на некоторую неподвижную ось z момента всех внешних сил равна нулю: dLz M z внеш 0 Lz const dt Момент импульса системы приблизительно сохраняется, если момент Мвнешн ограниченной по модулю внешней силы действует в течение короткого промежутка времени Δt: t dL M внеш dt L M внеш dt M внеш _ средн t 0 L const 0 Момент инерции твердого тела относительно неподвижной оси. Пусть твердое тело вращается с угловой скоростью вокруг неподвижной оси ОО', вдоль которой направим ось z неподвижной декартовой системы координат. Положительное направление оси z совпадает с направлением вектора . Найдем проекцию Lz момента импульса тела относительно произвольной точки О этой оси. Разделим все тело на большое число частиц массами mi . Положение частицы задается радиусом-вектором ri, проведенным к ней из точки О. Траекторией движения каждой частицы является окружность радиуса Ri с центром на оси вращения. Момент импульса L твердого тела относительно точки О: L Li ri , mi v i i i v i ri Пусть αi – угол между Li и осью z. Liz Li cos i ri , mi vi cos i ri mi vi sin 90 cos i Угловая скорость движения по окружности всех частиц одинакова и равна проекции на ось вращения z. В нашем случае z || . v i z Ri Из рисунка Ri ri cos i откуда Liz mi Ri2z 2 Lz Liz mi R z mi Ri z I zz i i i 2 i I z mi Ri2 i – момент инерции твердого тела относительно оси z. N I z lim mi Ri2 R 2dm R 2dV , dm dV , N i 1 V V где R – расстояние от элементарной массы dm до оси z, – плотность тела в данной точке, dV — элементарный объем. Момент инерции I характеризует распределение массы тела по объему. Аддитивность момента инерции Момент инерции относительно некоторой оси составного тела равен сумме моментов инерции его частей относительно той же оси. О О О' 1 I цил mR2 2 О' 1 I 1 mR2 цил 4 2 Теорема Штейнера. Устанавливает связь между моментами инерции тела относительно двух параллельных осей, одна из которых проходит через центр масс. a a, a z, zC , ri z, ri zC a, ri, r'i лежат в плоскости z, zC. ri ri a Момент инерции тела относительно центр масс оси z равен: 2 2 2 I z mi ri mi ri a mi ri 2mi ri a mi a 2 2 2 mi ri 2a mi ri a mi I C 2amrC ma , 2 где: rc mi ri m перпендикулярный оси zC вектор, проведенный от этой оси к центру масс тела – точке С. Поскольку центр масс тела лежит на оси zC , то rC 0 и 2 I z I C ma I C ma2 Это равенство выражает теорему Гюйгенса-Штейнера: Момент инерции I тела относительно произвольной оси равен сумме момента инерции IС относительно параллельной ей оси, проходящей через центр масс, и величины ma2, где m — масса тела, a – расстояние между осями. Пример: Моменты инерции некоторых тел относительно их осей симметрии: Однородный тонкий диск радиуса R массы m: r dr r О dm dS 2 rdr R 1 1 1 4 2 2 I диск r dm 2 r dr R R R mR2 2 2 2 S 0 2 3 Аналогичное выражение получим для сплошного цилиндра радиуса R: О О' 1 I цил mR2 2 Момент инерции однородного шара массы m радиуса R относительно оси, проходящей через центр шара. Разобьем шар на элементарные диски с параметрами: – угол между отрицательным направлением оси z и проведенным к краю диска радиусом шара R. Для диска: I шар 2 1 1 5 5 5 2 dI R sin d R 1 cos d (cos ) 2 2 0 0 8 2 4 3 2 2 5 R ( R ) R mR2 15 5 3 5 Момент инерции однородного тонкого стержня (нити) массы m и длины l относительно оси, перпендикулярной стержню и проходящей через его середину: О I (1) стерж 1 2 ml 12 О' Момент инерции однородного тонкого стержня (нити) массы m и длины l относительно оси, перпендикулярной стержню и проходящей через его конец: О I О' ( 2) стерж 1 2 ml 3 Момент инерции цилиндра массы m и радиуса R относительно прямой OO', которая параллельна оси симметрии и касается поверхности цилиндра, равен: zC О 1 3 2 2 I I C mR mR mR mR2 2 2 2 О' Уравнение вращения твердого тела вокруг неподвижной оси Пусть твердое тело вращается с угловой скоростью вокруг неподвижной оси ОО', совпадающей с осью z неподвижной декартовой системы координат. Обозначим через L момент импульса тела относительно произвольной точки О оси z, а через М — сумму моментов всех приложенных к телу внешних сил. Для твердого тела как системы частиц справедливо уравнение моментов: dL M dt или в проекции на ось z: dLz Mz dt Учитывая, что: Lz I zz получим уравнение вращения твердого тела вокруг неподвижной оси: dz I Mz dt или I z M z где I – момент инерции тела относительно оси z; z и z – проекции на ось z угловой скорости и углового ускорения соответственно; Mz – момент внешних сил относительно оси z. Пример. Цилиндр массы m и радиуса R может вращаться без трения вокруг неподвижной горизонтальной оси, совпадающей с его осью. На цилиндр намотана тонкая нерастяжимая невесомая веревка, за которую тянут с постоянной силой F. Найти угловую скорость и угловое ускорение цилиндра. Направим ось z вдоль оси вращения. I z M z 1 mR2 z RF 2 2F z mR t t dz z dt 2F 2 Ft 2 Ft z (t ) z dt dt z (0) mR mR mR 0 0 z (0) 0 Кинетическая энергия вращения твердого тела и работа внешних сил Разделим мысленно все тело на большое число частиц с массами mi, где i – номер частицы. Кинетическая энергия Т твердого тела равна сумме кинетических энергий составляющих его частиц: mi v i2 T , 2 v i ri mi 2 ri2 mi ri I 2 T 2 2 2 2 2 I 2 T , 2 где I – момент инерции тела относительно оси вращения, – угловая скорость. Работа внешней силы. Пусть на вращающееся вокруг неподвижной оси z твердое тело действует внешняя сила F, проекция момента которой на ось z равна Mz Найдем работу силы, рассматривая твердое тело как систему частиц. По теореме о кинетической энергии элементарная работа А всех сил, действующих на частицы, равна приращению dT кинетической энергии системы: A dT Суммарная работа всех внутренних сил равна нулю, так что работа А равна работе только внешней силы F: A AF Докажем это. Рассмотрим две произвольные частицы твердого тела 1 и 2. Силы взаимодействия F1 и F2 частиц друг с другом равны по величине и противоположны по направлению в соответствии с третьим законом Ньютона. Пусть в процессе движения твердого тела за бесконечно малый промежуток времени частицы 1 и 2 совершили перемещения dr1 и dr2. Работа сил F1 и F2 равна: Aвнутр F1dr1 F2dr2 F2 (dr2 dr1 ) F2d ( r2 r1 ) F2dr21 0, так как для двух частиц твердого тела r2 r1 r21 const Поскольку внутренние силы – это силы попарного взаимодействия частиц друг с другом, суммарная работа всех внутренних сил равна нулю. Таким образом: AF dT Найдем dT. I 2 Iz2 d Iz dz , dT d 2 2 ( z ) где I – момент инерции тела относительно оси z. Используя уравнение вращения твердого тела вокруг неподвижной оси: dz I Mz dt Idz M z dt где Mz – момент относительно оси z действующей на тело внешней силы F. где – угловая координата тела, d – угол, на который поворачивается тело за бесконечно малый промежуток времени dt, z d/dt – проекция угловой скорости на ось z. AF d N Mz M zz dt dt AF dT M z d Работа А силы F, совершаемая при повороте тела на конечный угол 0: 0 A M z d 0 Динамика плоского движения твердого тела Плоским называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Произвольное плоское движение можно представить как совокупность поступательного движения и вращения. Разбиение движения на поступательное и вращательное можно осуществить множеством способов, отличающихся значениями скорости поступательного движения, но соответствующих одной и той же угловой скорости. vC A R; v B A 2 R v B vС С R vС v B B R vC AR v B С R v B B R A B С Обобщим приведенные соотношения. Пусть скорость поступательного движения равна v0. Примем одну из точек, лежащих на оси вращения, за начало координат О. Составляющую скорости точек тела, обусловленную вращением, можно представить в виде векторного произведения: r , где r – радиус-вектор, проведенный из точки О в данную точку тела. Тогда для скорости точек тела относительно неподвижной системы отсчета получим: v vO r , Элементарное перемещение твердого тела при плоском движении всегда можно представить как поворот вокруг так называемой мгновенной оси вращения – прямой, неподвижной в данный момент в некоторой инерциальной системе отсчета. Эта ось может находиться внутри либо вне тела. мгновенная ось вращения Удобным оказывается разбиение произвольного плоского движения на поступательное, происходящее со скоростью центра масс vC, и вращение вокруг оси, проходящей через этот центр. В этом случае для описания движения используются два уравнения: уравнение движения центра масс и уравнение вращения тела вокруг оси, проходящей через центр масс (ось z): dv C m Fвнеш dt В системе центра масс выбранная ось вращения z неподвижна, движение твердого тела – вращение вокруг неподвижной оси. Для его описания можно использовать уравнение: dz I Mz, dt где I – момент инерции тела относительно оси вращения z, которая является осью симметрии тела, Mz – проекция на ось z суммы моментов всех внешних сил (момент сил относительно оси z). Кинетическая энергия тела при плоском движении Представим плоское движение тела как наложение поступательного движения со скоростью vО некоторой точки О и вращения вокруг оси, проходящей через эту точку, с угловой скоростью . В этом случае скорость i-той элементарной массы тела определяется формулой vi vO ri , 2 1 2 1 Ti mi v i mi vO ri 2 2 Просуммировав Ti по всем кинетическую энергию тела T: элементарным массам, найдем 2 2 1 T Ti mi vO 2vO ri ri 2 1 2 1 2 T vO mi vO mi ri mi ri 2 2 2 2 1 2 1 1 2 2 2 2 mi m, ri Ri , 2 mi ri 2 mi Ri 2 I vO mi ri vO , mi ri vO ,mrC ri 2 2ri2 sin2 i где rC – радиус-вектор центра масс, проведенный из точки О. 1 2 1 2 T mvO mvO rC I 2 2 Если в качестве точки О взять центр масс тела, то rC будет равен нулю: 1 2 1 T mv C I C 2 2 2 Здесь vС – скорость центра масс, IC – момент инерции тела относительно оси, проходящей через центр масс. Роль силы трения при качении однородных цилиндрических тел. Рассмотрим задачу. Сплошной однородный цилиндр массы m и радиуса r скатывается без проскальзывания по наклонной плоскости, составляющей угол α с горизонтом. Коэффициент трения скольжения между цилиндром и наклонной плоскостью равен μ. Найти ускорение а центра масс – точки С, угловое ускорение цилиндра и действующую на него силу трения покоя Fтp в зависимости от угла α. Уравнение поступательного движения центра масс в неподвижной системе отсчета x1y1 имеет вид: ma mg Fтр N , a dvC dt В проекциях на оси координат: (1) Поскольку линии действия силы тяжести mg и силы нормальной реакции опоры N проходят через ось вращения z, моменты этих сил относительно оси z равны нулю. В системе центра масс суммарный момент сил инерции относительно центра масс равен нулю. Тогда уравнение вращения цилиндра вокруг оси z в примет следующий вид: I M тр rFтр , ( 2) где Мтр – момент силы трения относительно оси z, – совпадающий с z модуль углового ускорения цилиндра (z = ), I – момент инерции цилиндра относительно оси симметрии z. 1 2 I mr 2 В отсутствие проскальзывания a r (3) Решив совместно уравнения (1)-(3), получим При отсутствии проскальзывания между цилиндром и наклонной плоскостью действующая на цилиндр сила трения Fтp, являясь силой трения покоя, не может превысить величины μN. С помощью этого условия определим значения угла α, при которых возможно качение без проскальзывания: Сила трения покоя приложена к точкам поверхности цилиндра, скорость которых в неподвижной системе отсчета равна нулю, эта сила не совершает работы и не вносит вклад в изменение кинетической энергии тела. При больших значениях угла α сила трения покоя становится недостаточной для обеспечения качения без проскальзывания, и чистое качение становится невозможным. В этих условиях на тело действует сила трения скольжения Fтр = μmg cos α, направленная вдоль наклонной плоскости противоположно скорости центра масс цилиндра. Для решения задачи следует вновь начать с уравнений (1-2). Если α 0, ускорение центра масс, угловое ускорение и сила трения покоя Fтp стремятся к нулю. Это означает, что при отсутствии скольжения однородное цилиндрическое тело катится по горизонтальной плоской поверхности равномерно и прямолинейно, не испытывая силы сопротивления. Такое движение может продолжаться бесконечно долго. Вывод о том, что однородное цилиндрическое тело катится по горизонтальной плоской поверхности равномерно и прямолинейно, не испытывая силы сопротивления, относится к идеализированной модели абсолютно твердых тел. В реальных условиях цилиндрическое тело и поверхность деформируются. Возникает сила сопротивления, замедляющая движение. Кинетическая энергия цилиндра будет израсходована на работу против сил деформации, и в конечном цилиндр остановится. Горизонтальная составляющая силы сопротивления называется силой трения качения.