Lekciya8

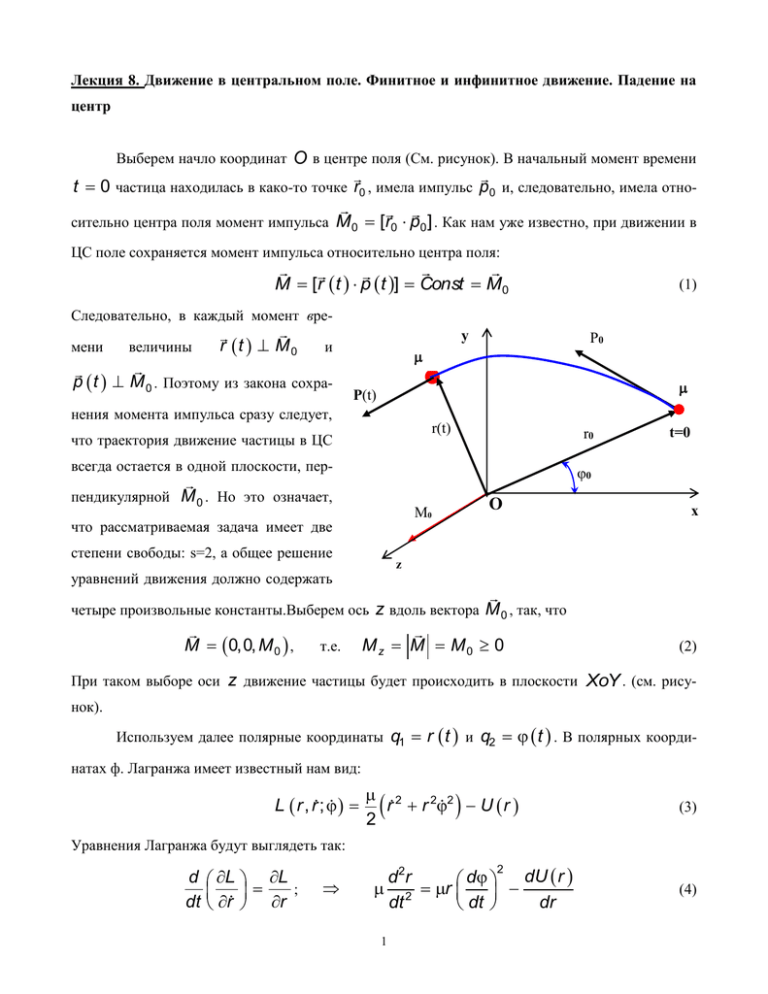
Лекция 8. Движение в центральном поле. Финитное и инфинитное движение. Падение на
центр
Выберем начло координат O в центре поля (См. рисунок). В начальный момент времени
t  0 частица находилась в како-то точке r0 , имела импульс p0 и, следовательно, имела относительно центра поля момент импульса M 0  [r0  p0 ] . Как нам уже известно, при движении в
ЦС поле сохраняется момент импульса относительно центра поля:
M  [r  t   p  t ]  Const  M 0
Следовательно, в каждый момент времени
величины
r t   M 0
.
и
p  t   M 0 . Поэтому из закона сохра-
y
(1)
P0

P(t)

нения момента импульса сразу следует,
r(t)
что траектория движение частицы в ЦС
r0
всегда остается в одной плоскости, пер-
t=0
0
пендикулярной M 0 . Но это означает,
O
0
что рассматриваемая задача имеет две
степени свободы: s=2, а общее решение
x
z
уравнений движения должно содержать
четыре произвольные константы.Выберем ось z вдоль вектора M 0 , так, что
M   0,0, M 0  ,
т.е.
M z  M  M0  0
(2)
При таком выборе оси z движение частицы будет происходить в плоскости XoY . (см. рисунок).
Используем далее полярные координаты q1  r  t  и q2    t  . В полярных координатах ф. Лагранжа имеет известный нам вид:
L  r , r ;  
 2
r  r 22  U  r 
2


(3)
Уравнения Лагранжа будут выглядеть так:
d
dt
 L   L
;


 r  r
dU  r 
d 2r
d 
 2  r 


dr
dt
 dt 
2

1
(4)
d  L  L

;
dt    

Поскольку ф. Лагранжа не зависит явно от угла 

 
d 2
r  0
dt
 L /   0 , то координата 
(5)
является
циклической. Поэтому из уравнения Лагранжа (5) сразу следует, что сохраняется обобщенный
импульс: p  
L
 Const . Как нам известно, величина p  r 2  M z . Но при нашем

выборе осей координат M z  M 0 . Поэтому уравнение (5) выражает закон сохранения момента
импульса относительно центра поля:
r 2  t    t   M 0
(6)
Закон сохранения момента при плоском движении допускает наглядную геометрическую
интерпретацию. Выражение
1
r  r d    df есть площадь сектора, образованными двумя бес2
конечно близкими радиус-векторами с углом d между ними и элементом дуги траектории.
Поэтому закон сохранения момента импульса (6) можно записать в виде:
M
df
 0  Const
dt
2
(7)
Производную f называют секториальной скоростью, а закон сохранения момента импульса
иногда называется интегралом площадей: за равные промежутки времени радиус-вектор движущейся точки описывает равные площади (второй закон Кеплера).
Из формулы (6) получаем, что
d  t 
M
 20 0
dt
r  t 
(8)
Следовательно, угол   t  монотонно возрастает со временем, т.е. угловая скорость частицы
    t   0 . Из (8) сразу следует, что наибольшее значение угловая скорость достигает при
наименьшем расстоянии частицы от центра поля:
2
max  t   M 0 / rmin
t 
(9)
Полное решение задачи о движении в ЦС проще всего получить, используя законы сохранения энергии и импульса:
2
  2
r  r 22  U  r   E0

 2
 r 2  M 0


(10)
Из второго уравнения (10) сразу находим угловую скорость
 t  
M0
r 2  t 
(11)
Подставляя (11) в первое уравнение (10) получаем:
 2
r  Uef f  r   E0
2
(12)
Здесь Uef f  r  - так называемая «эффективная» потенциальная энергия частицы в ЦС поле:
Uef f  r ; M 0 
M 02
 U r  
2r 2
(13)
M 02
 0 называют центробежной энергией. Соответствующая её центробежная сиВеличину
2r 2
ла всегда является силой отталкивания:
d  M 02  r M 02 r
r
Fцб   
 
 4~ 4.
2 
dr  2r  r 2 r
r
(14)
Только в тех случаях, когда M 0  0 , величина эффективной потенциальной энергии совпадает
с истинной потенциальной энергией частицы:
Uef f  r ; M0  0   U  r 
(15)
Уравнение (12) для радиального движения частицы формально похоже на одномерное
уравнение движение частицы с одной степенью свободы, изученное нами ранее. Однако следует
помнить, что в рассматриваемой задаче величина r  t  всегда положительна: r  t   0 и точка
r  t   0 является центром поля. Кроме того, если r  t   0 , то это не точка остановки, как
при истинном одномерном движении, а точка остановки радиального движения. Границы области движения (по расстоянию от центра) определяются условием:
U r  
M 02
 E0
2r 2
Уравнение
3
(16)
M 02
U r  
 E0
2r 2
(17)
определяет минимальное rmin и максимальное rmax расстояния от частицы до центра поля.
Следует обратить внимание на то обстоятельство, что величины rmin и rmax зависят от E0 и
M 0 , как от параметров рассматриваемой задачи. Из уравнения (12) сразу находим, что
r 
dr
2

E0  Uef f  r 
dt

(18)
Разделяя переменные, получаем:
t 
r


 


r0
dr 
2
E0  Uef f  r 


r


 



r0
dr 
(19)
M 02
2
E0  U  r   2r 2

Формула (19) определяет (в неявном виде) зависимость расстояния от частицы до центра поля в
любой момент времени t . Переписав уравнение (11) и (18) в виде
d 
M0
dt ,
r 2  t 
dr  
2
E0  Uef f  r dt ,

получаем уравнение траектории:
 r  
r


 


r0
M0
dr 
r 2
 0 
2 E0  Uef f  r 
r








r0
M0
dr 
r 2
2 E0  U  r  
M 02
2
 0
(20)
r
Здесь  0 - начальный азимутальный угол. Формула (20) определяет уравнение траектории
    r  частицы в плоскости XoY в полярных координатах. Таким образом, формулы (19)
и (20) полностью решают задачу о движении частицы  в произвольном ЦС поле U  r  . Вся
сложность решения такого рода задач смещается из плоскости физической в математическую
плоскость.
Из уравнения (17) находим точки поворота. Если это уравнение имеет всего один корень
r  rmin  E0  , то движение частицы инфинитно: её траектория, начинаясь в точке r0 , пройдет
4
через некоторое время точку наибольшего сближения rmin и затем уйдет на бесконечность. Если уравнение (17) имеет два корня r  rmin  E0  и r  rmax  E0  , то движение частицы финитно. В этом случае траектория частицы целиком лежит внутри кольца rmin  r  rmax ,
ограниченного окружностями r  rmin  E0  и r  rmax  E0  .
Но это вовсе не означает, что при финитном движении траектория частицы непременно
является замкнутой кривой. За время, в течение которого расстояние r изменяется от величины
r  rmax до r  rmin и обратно до r  rmax , радиус вектор повернется на угол (согласно
формуле (20)) на величину
 
rmax



2




rmin
M0
dr
r2
2 E0  U  r  
M 02
2
.
(21)
r
Условие замкнутости траектории выражается условием:   2m / n  n  m  . Тогда, через n повторений периода времени радиус вектор точки, сделав m полных оборотов, совпадет
со своим первоначальным значением, т.е. траектория замкнется. Можно строго показать, что
такая ситуация возможна только для двух потенциалов: U  r  ~ 1/ r (задача Кеплера) и
U  r  ~ r 2 (пространственный осциллятор).
В заключение этого раздела рассмотрим вопрос о возможности падения частицы на
центр поля, когда поле носит характер притяжения.
Сначала рассмотрим простейший случай, когда M 0  0 . Это будет иметь место, когда
либо начальная скорость равна нулю ( p 0  0 ), либо когда вектор p0 коллениарен вектору r0 .
Понятно, что во всех этих случаях движение будет прямолинейным:   0  Const - это
уравнение прямой в полярных координатах.
Если p 0  0 или p0  r0 , то падение на центр неизбежно. Если же начальная скорость направлена от центра, то возможны два случая:
1. Уравнение U  r   E0 не будет иметь решения при r  r0 . Тогда частица удалится
на бесконечность.
5
2. Уравнение U  r   E0 будет имеет корень r  rmax . Тогда траектория частицы будет состоять из двух частей. На первом участке частица будет удаляться от центра до расстояния r  rmax  E0  . В точке r  rmax  E0  частица, имея нулевую скорость, под действием
сил притяжения начнет двигаться в обратную сторону и в конечном итоге упадет на центр поля
притяжения.
Наконец рассмотрим вопрос о возможности падения на центр в общем случае, когда
M 0  0 . Наличие центробежной энергии, стремящейся при r  0 к  по закону ~ 1/ r 2 ,
делает обычно невозможным проникновения частиц к центру поля, даже если это поле притяжения. Теоретически, падение на центр возможно лишь тогда, если U  r  достаточно быстро
стремиться к  при r  0 . Перепишем условие, определяющее область допустимых расстояний, в виде:
M 02
 r 2U  r   E0r 2
2
(22)
Необходимо, чтобы это условие выполнялось вплоть до точки r  0 . Полагая в последней
формуле r  0 , запишем её так:
r U r 
2
r 0
Здесь учтено, что при r  0 , величина E0r
2
M 02

2
(23)
 0 , независимо от значения полной энергии
E0 . Последнее неравенство может выполняться в двух случаях:
1. Если U  r  ~ 
1
, при n  2
rn
2. Если U  r  ~ 

,
r2
(24)
при   M 0 / 2
2
(25)
Конечно, полученные ограничения на вид потенциальной энергии, означают только, что
при их выполнении падение частицы на центр возможно в принципе, т.е. они являются необходимыми условиями падения на центр поля. Но их выполнение вовсе не означает, что в процессе
движения частица достигнет центра поля. Это зависит от начальных условий. Например,
начальные условия в любом центральном поле можно выбрать так, чтобы частица вращалась по
окружности вокруг центра поля. В этом случае падения на центр поля не будет, даже если установленные выше условия будут выполнены.
6