Аналитическая геометрия на плоскости.

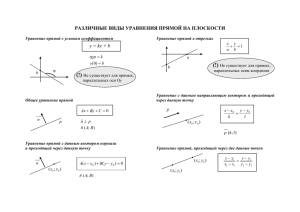
Аналитическая геометрия
на плоскости.
§1 Уравнение линии на плоскости.
Основная задача - исследовать
математическими методами формы,
расположения и свойства данной линии.
Определение: Линия на плоскости есть
множество точек, обладающих некоторыми
геометрическими свойствами,
исключительно им присущими.
Определение: Уравнением линии (кривой) на
плоскости ОХУ называется уравнение,
которому удовлетворяют координаты Х и У
каждой точки данной линии и не
удовлетворяют координаты точки, не
лежащей на этой линии.
!т. М (х,у)передвигается по линии, х и у
удовлетворяя, изменяясь уравнению
линии, поэтому координаты т. М (х ,у)
называются текущими координатами точки
линии.
Основные задачи.
1. Дана линия, рассмотрим как множество
точек. Составить уравнение этой линии .
2. Дано уравнение некоторой линии. Изучить
по этому уравнению ее геометрические
свойства(определить форму и
расположение).
Определение: Линия называется линией или
кривой n-го порядка, если она
определяется уравнение n-ой степени
относительно текущих прямоугольных
координат.
Х +У = 5 прямая
Х² = У парабола
У = Х³ кубическая парабола
§2 Прямая линия
п.1 Общее уравнение прямой.
Задача: М 0 ( x0 , y0 ), n  ( A, B)
M 0  , n  
 ?
М0
n
M
Решение:М ( x, y )  текущая точка прямой
M 0 M  ( x  x0 , y  y0 )
ò .ê.n  , òî
n  M 0M , n  M 0M  0
A( x  x0 )  B( y  y0 )  0
Ax  B y  C  0
Геометрический смысл А и В: n  ( A, B)  
Определение: n  нормаль прямой
п.2 Уравнение прямой «в отрезках».
Пусть C  0, A, B  0, тогда
Ax  B y  C | : ( C )
X
Y

1
C C
A
B
C
C
  a,   b
A
B
x
y

1
a
b
- уравнение прямой «в отрезках»
a, b - отрезки, отсекаются прямой на осях
координат
x0 y b
y 0 x a
п.3 Каноническое уравнение прямой.
Задача:
S  (m, n)
M 0 ( x0 , y0 ),  S , M 0  
?

S
M
M0
Решение:
M ( x, y )  
M 0 M  ( x  x0 , y  y0 )
S коллинеарен M 0 M  координаты
пропорциональны.
x  x0 y  y0

m
n
п.4 Параметрические уравнения
прямой.
x  x0 y  y0

 t;
m
n
t  ïàðàìåòð
 x  x0  mt
t  (;)

 y  y0  nt
п.5Уравнение прямой проходящей
через две заданные точки.
Задача: M 1 , M 2  

M2
?
Решение:
M ( x, y )
M
M1
M 1M  ( x  x1 , y  y1 )
M 1M 2  ( x2  x1 , y2  y1 )
M 1M
и M 1M 2 коллинеарные
x  x1
y  y1

x2  x1 y2  y1
п.6 Уравнение с угловым
коэффициентом.
Задача 1: Рассмотрим прямую, проходящую
через начала координат.
  (0 x ^  )
?
y
y
0


x
x
Решение: M ( x, y) - текущая точка линии.
y  x  tg;

tg  k
определяет направление прямой
Определение: k - называется угловой
коэффициент прямой.
Задача 2: Рассмотрим прямую, проходящую
через точку B (0, b).
b - отрезок, отсекаемый на оси OY .
  (OX ^ )
y

y
B

M ( x, y )

0
x
x
y  b  x  tg
y  kx  b
если k  0,   00  y  b

если y  , òî   OX , x  b
2
a -абсцисса следа на оси OX .
п.7 Угол между двумя прямыми.
   2  1
 1 : y  k1 x  b1
 2 : y  k 2 x  b2
tg 2  tg1
tg  tg ( 2  1 ) 
1  tg1  tg 2
k 2  k1
tg 
1  k1k 2
1
y
2
1
0
2
2
1
x
п.8 Условия параллельности и
перпендикулярности двух прямых.
a ) 1  2  1   2  tg1  tg 2  k1  k 2
1   2
1  k1k 2
   90 ; ctg 
0
k 2  k1
0
k1  k 2  1
á ) 1 : A1 x  B1 y  D  0 n1  ( A1 , B1 )
n2  ( A2 , B2 )
 : A xB yD 0
2
2
2
 1  2 ; n1  n2
 1   2 ; n1  n2
A1 A2  B1 B2  0
A1
B1

A2
B2
1
2
n1
n2
n2 
2
1
n1
п.9 Точка пересечения двух прямых.
 1 : A1 x  B1 y  D1  0
 2 : A2 x  B2 y  D2  0
 1   2  M ( x0 , y0 )
M ( x0 , y0 )  ?
M   1  A1 x0  B1 y0  D1  0
M   2  A2 x0  B2 x0  D2  0
( x0 ; y0 ) есть решение системы уравнений:
 A1 x0  B1 y0  D1  0

 A2 x0  B2 y0  D2  0
п.10 Взаимное расположение двух
прямых.
если прямые пересекаются, то система имеет
единственное решение (п.9);
если прямые параллельны, то система не
имеет решения;
если прямые совпадают, то система имеет
бесконечно много решений.
п. 11 Уравнение прямой, проходящей
через данную точку в данном
направлении.
Дано:   (^ ox);
M 0 ( x0 , y0 )  
 ?
y


M 0 ( x0 , y0 )
x
y  kx  b
y0  kx0  b
y  y0  k  ( x  x0 ) *
п.12 Уравнение пучка прямых.
если k дано, то уравнение * определяет одну
прямую, если k – меняем, то уравнение *
определяет пучок прямых, проходящий
через т. M1 ( x1 , y1 ) .
п. 12 Расстояние от точки до прямой.
 : Ax  By  D  0; M1 ( x1 , y1 )
d 
Ax1  By1  D
A2  B 2
Чтобы определить расстояние от точки до
прямой, надо в левую часть общего
уравнения прямой подставить координаты
данной точки, взять модуль результата, и
разделить его на длину нормали прямой
( n  A2  B 2 ).
§ Применение линейной зависимости в
экономических задачах.
Пример 1: Издержки производства 100 шт.
некоторого товара составляют 300 тыс. руб, а
500 шт. – 600 тыс. руб. Определить издержки
производства 400 шт. товара при условии, что
функция издержек линейная.
Решение: если функция линейная, то графиком
её является прямая. В нашем случае
проходящая через точки (100,300);(500,600).
x  øò . y - издержки пр-ва (в тыс. руб).
y  y1
x  x1
y  300
x  100




y2  y1 x2  x1
600  300 500  100
y  300 x  100
3
3


 y  300  ( x  100)  y  x  225
300
400
4
4
ïðè
x  400
y  525 òûñ .ðóá.
Задача 2: Издержки перевозки двумя
видами транспорта выражаются функциями
y = 150 + 50x и y =250+25x,
где x - расстояние перевозок в сотнях км.
y – транспортные расходы.
Определить, начиная с какого расстояния
более экономичным становиться второй
вид транспорта.
y

 y  150  50 x x  4


 y  250  25 x y  350

400
300
200
100
4
x
Ответ: при расстоянии превышающим
400 км, более экономичны перевозки
вторым видом транспорта.