ПРИЛОЖЕНИЕ Расчетно-графическое задание
advertisement
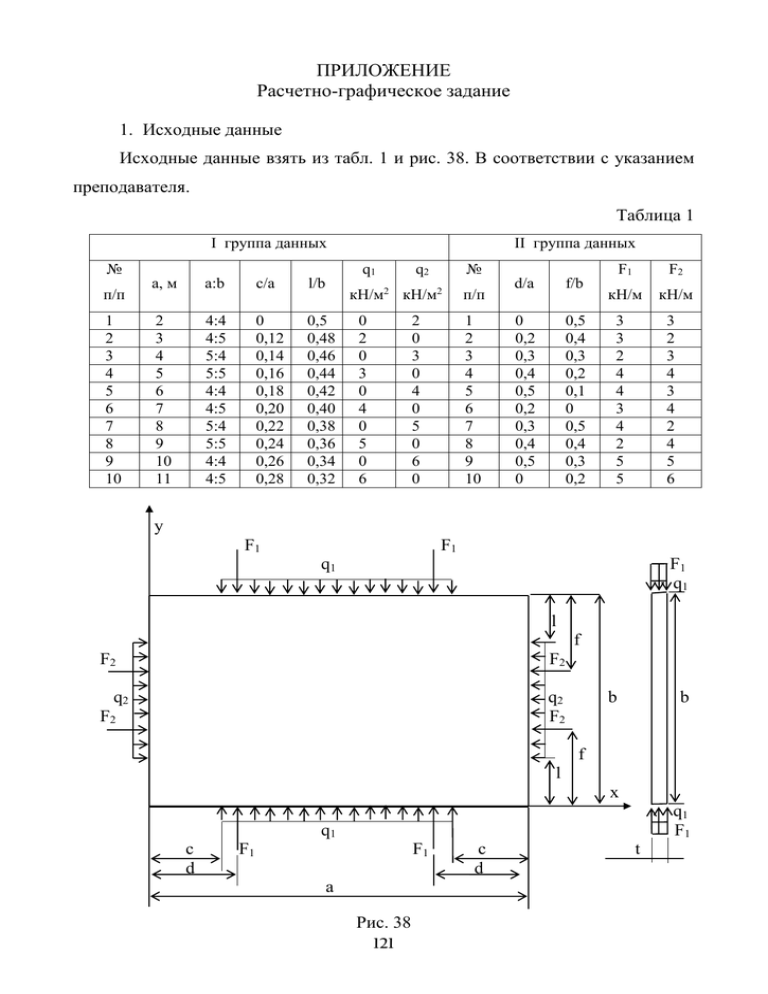
ПРИЛОЖЕНИЕ Расчетно-графическое задание 1. Исходные данные Исходные данные взять из табл. 1 и рис. 38. В соответствии с указанием преподавателя. Таблица 1 І группа данных № п/п 1 2 3 4 5 6 7 8 9 10 ІІ группа данных q1 a, м a:b c/a l/b 2 3 4 5 6 7 8 9 10 11 4:4 4:5 5:4 5:5 4:4 4:5 5:4 5:5 4:4 4:5 0 0,12 0,14 0,16 0,18 0,20 0,22 0,24 0,26 0,28 0,5 0,48 0,46 0,44 0,42 0,40 0,38 0,36 0,34 0,32 № q2 кН/м2 кН/м2 0 2 0 3 0 4 0 5 0 6 2 0 3 0 4 0 5 0 6 0 п/п 1 2 3 4 5 6 7 8 9 10 d/a f/b 0 0,2 0,3 0,4 0,5 0,2 0,3 0,4 0,5 0 0,5 0,4 0,3 0,2 0,1 0 0,5 0,4 0,3 0,2 F1 F2 кН/м кН/м 3 3 2 4 4 3 4 2 5 5 3 2 3 4 3 4 2 4 5 6 y F1 F1 q1 F1 q1 l f F2 F2 q2 q2 F2 F2 b b f l х q1 F1 q1 c d F1 F1 a Рис. 38 121 c d t Для пластинки (рис. 38) необходимо: − в соответствии с заданными в таблице 1 соотношениями вычислить все размеры; − начертить пластинку в масштабе; − разбить пластинку сеткой с квадратными ячейками в соответствии с заданным соотношением a : b и пронумеровать ее узлы с учетом симметрии, начиная с внутренних и заканчивая законтурными; − составить дифференциальные уравнения в конечных разностях для внутренних узлов четверти сетки и привести подобные в них с учетом симметрии; − определить функции напряжений в контурных и законтурных узлах сетки и подставить их значения в уравнения; − с помощью компьютера решить систему уравнений относительно значений функции напряжений во внутренних узлах сетки; − вычислить напряжения в узлах сетки и построить их эпюры для пластинки. 2. Пример расчета Выполнить расчет пластинки, приведенной на рис. 1 при исходных данных табл. 2. Таблица 2 q1 a, м a:b c/a l/b 2,5 5:4 0,22 0 q2 кН/м2 кН/м2 8 4 d/a f/b 0,3 0,5 F1 F2 кН/м кН/м 10 3 Решение Схема пластинки и нагрузка в соответствии с данными табл. 2 приведена на рис. 39. Отметим, что в данном случае f b / 2 , т.е. точки приложения сил F2 совпали и в середине пластинки действует сила 2 F2 2 3 6 кН/м. 122 y F1=10 кН/м q1=8 кН/м2 F1 q2 q2=4 кН/м2 2F2 2F2=10 кН/м b=2 м f=1 м х q1 c=0.55 м F1 d=0.75 м F1 a=2.5 м Рис. 39 Замечание. При l b / 2 соответствующая распределенная нагрузка отсутствует. В соответствии с заданным соотношением a : b 5 : 4 разбиваем сторону a 2 ,5 м на 5 частей, а сторону b 2 м на 4 части. Получаем сетку (рис. 40) с квадратными ячейками. Шаг сетки составляет h 2,5 2 0,5 м. Пунктиром 5 4 дополняем сетку на один шаг за контур. Нумеруем узлы в четверти сетки. Начинаем с внутренних узлов (1, 2, 3, 4), затем на контуре (5 … 9) и далее за контуром (10 … 15). Узлы в остальных четвертях сетки нумеруем так, чтобы их номера совпадали с точностью до штрихов с номерами симметричных узлов. 123 y 13 14 15 15 14 13 12 7 8 9 9 8 7 12 11 6 3 4 4 3 6 11 10 5 1 2 2 1 5 10 ось симметрии 11 6 3 4 4 3 6 11 h=0.5 м 12 7 8 9 9 8 7 12 13 14 15 15 h=0.5 м 14 13 ось симметрии Рис. 40 С учетом симметрии составляем дифференциальное уравнение в конечных разностях (73) для каждой внутренней точки в четверти контура по схеме, приведенной на рис. 41. Эта схема указывает, с каким множителем необходимо брать значение функции для точки, соответственно расположенной относительно точки, в которой записывается уравнение (73). - 20 - (-8) - 2 - 1 Рис. 41 124 Итак получаем: для т. 1: 201 8 2 3' 5 3 2 4' 6' 6 4 2'' 8' 10 8 0; для т. 2: 202 8 2'' 4' 1 4 2 4''' 3' 3 4'' 1'' 9' 5 9 0; для т. 3: 203 8 4 1 6 8 2 2 5 7 9 4'' 3' 11 14 0; для т. 4: 204 8 4'' 2 3 9 2 2'' 1 8 9'' 3'' 4' 6 15 0. Раскрываем скобки и, учитывая, что в симметричных точках значения функции напряжений одинаковы i i' i'' i''' , получаем: 201 7 2 163 4 4 85 4 6 28 10 0; 71 12 2 43 12 4 5 29 0; 81 2 2 213 7 4 25 8 6 2 7 88 29 11 14 0; (161) 21 6 2 73 13 4 6 28 69 15 0. Образуем раму (рис. 42) с осями, соответствующими контуру рамы и строим для нее эпюры изгибающих моментов и продольных сил от заданной на контуре нагрузки (рис. 43). y F1=10 кН/м q1=8 кН/м2 F1 7 0.5 м 0.5 м q2=4 кН/м2 q2 6 2F2=10 кН/м 2F2 b=2 м 5 0.5 м 1м 6 7 0.5 м 8 9 9 8 q1 0.55 м 0.75 м F1 F1 a=2.5 м Рис. 42 125 7 х 3 7.8 7.8 12.29 3 12.29 М 5 12.29 5 12.29 3 7.8 7.8 3 7.0 15.6 15.6 N 7.0 Рис. 43 Благодаря расположению шарниров во всех узлах рамы, каждый ее стержень при определении изгибающих моментов может рассматриваться как отдельная балка на двух шарнирных опорах (рис. 44). Отметим, что при построении эпюр изгибающих моментов в балках необходимо в первую очередь определить моменты на границах участков нагружения (на границах распределенной нагрузки, в точках приложения сосредоточенных сил). После этого определяются моменты в тех точках, которые соответствуют узлам сетки. Продольная перпендикулярной сила к в стержне нему балке, рамы равна например в опорной реакции вертикальном стержне рассматриваемой задачи N R1 15,6 , а в горизонтальном N R2 7 . 126 в 0.75 м 0.55 м R2 F1=10 кН/м q1=8 кН/м2 F1 7 R2 7 0.5 м 8 0.5 м 9 9 8 R1 2.5 м R1 2F2=6 кН/м q2=4 кН/м R1 2 7 7 6 0.5 м 5 0.5 м R2 R1 6 2м R2 Рис. 44 На основании соотношений (74) получаем выражения для функции напряжений в законтурных точках: 10 11 14 15 1 2h N 5 1 2 0,5 15 ,6 1 15 ,6; 3 2h N 6 3 2 0,5 15 ,6 3 15 ,6; 3 2h N 8 3 2 0,5 7 3 7; (162) 4 2h N 9 4 2 0,5 7 4 7. После подстановки этих выражений в (161) получаем: 211 7 2 163 4 4 85 4 6 28 15 ,6 0; 71 12 2 43 12 4 5 29 0; 81 2 2 233 7 4 25 8 6 2 7 88 29 22 ,6 0; 21 6 2 73 14 4 6 28 69 7 0. Значения функции напряжений в точках на контуре определяем по эпюре изгибающих моментов: 5 M 5 5 ,0 ; 6 M 6 3, 0 ; 8 M 8 7 ,8 ; 9 M 9 12,29 . 7 M 7 0 ; 127 С учетом этих значений уравнения конечных разностей принимают такой вид: 211 7 2 163 4 4 28 0; 71 12 2 43 12 4 29 ,58 0; (163) 81 2 2 233 7 4 74 ,42 0; 21 6 2 73 14 4 62 ,14 0. Решаем систему уравнений с помощью ПЭВМ. Расчеты выполняются в программе MSExel пакета MSOffice, или Open Office. org Calc пакета Open Office. оrg. Для решения системы линейных уравнений используем метод, в соответствии с которым уравнения записываются в матричной форме: A X B , (164) где A − квадратная матрица коэффициентов при неизвестных, X − матрица-столбец неизвестных, B − матрица-столбец правых частей уравнений. Матричная форма записи системы (163) принимает такой вид: 4 φ1 28 21 7 16 7 12 4 12 φ 2 29.58 . 8 2 φ3 23 7 74.42 2 6 7 14 φ 4 62.14 Решение системы (164) имеет вид: X A 1 B . Таким образом, для получения решения системы уравнений (163) необходимо: 1) сформировать матрицу коэффициентов правых частей B ; 2) вычислить обратную матрицу A ; 1 128 A и матрицу-столбец 3) получить матрицу-столбец искомых значений неизвестных X как результат умножения обратной матрицы A 1 на матрицу-столбец B правых частей. Это можно осуществить следующим образом: − в ячейки А1-D4 ввести значения матрицы А; − в ячейки F1-F4 ввести значения матрицы-столбца B ; − установить курсор на ячейку А6, с которой будет начинаться обратная матрица и щелкнуть левой кнопкой мышки; − щелкнуть на иконке « f x » в строке формул, по которому вызывается Мастер функций; − в окне Мастера функций выбрать в поле «Категория» значение «Массив», в поле «Функции» отметить функцию «INVERSE», которая вычисляет обратную матрицу, и щелкнуть по иконке «Далее»; − в центральной части окна Мастера функций появится поле, в которое необходимо ввести диапазон ячеек исходной матрицы A . Для этого можно щелкнуть по иконке со стрелкой, которая находится правее данного поля (она минимизирует размеры окна Мастера функций), отметить мышкой или иконками со стрелками при нажатой клавише «Shift» ячейки А1-D4 матрицы коэффициентов, снова щелкнуть по иконке со стрелкой, которая находится правее поля (она максимизирует размеры окна Мастера функций); − щелкнуть по иконке «OK» Мастера функций. В ячейках А6-D9 появятся коэффициенты обратной матрицы A ; 1 − установить курсор на ячейку F6, с которой будет начинаться столбец искомых значений неизвестных значений функции напряжений; − щелкнуть на иконке « f x » в строчке формул, по которой вызывается Мастер функций; 129 − в окне Мастера функций выбрать в поле «Категория» значение «Массив», в поле «Функция» отметить функцию «MMULT», которая вычисляет произведение двух матриц и щелкнуть по иконке «Далее»; − в центральной части окна Мастера функций появятся два поля, в первое из которых необходимо ввести диапазон ячеек обратной матрицы A : А61 D9, а во второе – диапазон ячеек матрицы-столбца правых частей B : в каждом из двух полей: щелкнуть по иконке со стрелкой, которая находится справа от данного поля (она минимизирует размеры окна Мастера функций), отметить мышкой или иконками со стрелками при нажатой клавише «Shift» нужные ячейки, снова щелкнуть по иконке со стрелкой, которая находится справа от поля (она минимизирует размеры окна Мастера функций); − щелкнуть по иконке «OK» Мастера функций. В ячейках F6-F9 появятся результаты расчета – значения функции напряжений в точках 1 … 4. В рассмотренном примере получаем: 1 11,60 ; 2 15,42 ; 3 10,37 ; 4 14,58 . Из (162) получаем значения функции в законтурных точках: 10 11,60 15,6 4,0 ; 11 10,37 15,6 5,23 ; 14 10,37 7 3,37 ; 15 14,58 7 7,58 ; 13 6 2hN7 3 2 0,5 7 4 ; 12 8 2hN7 7,8 2 0,5 15,6 7,8 . Теперь переходим к определению нормальных и касательных напряжений по формулам (75): x 1 3' 21 3 / h 2 10 ,37 2 11,6 10 ,37 4 9,84 ; x 2 4' 2 2 4 / h 2 14 ,58 2 15 ,42 14 ,58 4 6,72 ; x 3 1 23 8 / h 2 11,6 2 10 ,37 7 ,8 4 5,36 ; 130 x 4 2 2 4 9 / h 2 15 ,42 2 14 ,58 12 ,29 4 5,80 ; x 5 6' 25 6 / h 2 3 2 5 3 4 16 ,0 ; x 6 5 26 7 / h 2 5 2 3 0 4 4,0 ; x 7 6 27 13 / h 2 3 2 0 4 4 4,0 ; x 8 3 28 14 / h 2 10 ,37 2 7 ,8 3,37 4 7 ,44 ; x 9 4 29 15 / h 2 14 ,58 2 12 ,29 7 ,58 4 9,68 . y 1 5 21 2 / h2 5 2 11,6 15,42 4 11,12 ; y 2 2'' 22 1 / h2 15,42 2 15,42 11,6 4 15,28 ; y 3 4 23 6 / h2 14 ,58 2 10 ,37 3 4 12 ,64 ; y 4 4'' 24 3 / h2 14 ,58 2 14 ,58 10 ,37 4 16 ,84 ; y 5 1 25 10 / h 2 11,6 2 5 4 4 9,6 ; y 6 3 26 11 / h 2 10 ,37 2 3 5,23 4 3,44 ; y 7 8 27 12 / h2 7,8 2 0 7,8 4 0 ; y 8 9 28 7 / h2 12 ,29 2 7,8 0 4 13,24 ; y 9 9'' 29 8 / h2 12 ,29 2 12 ,29 7,58 4 17 ,96 . xy 1 4' 6' 6 4 / 4h2 0 ; xy 2 4''' 3' 3 4'' / 4h 2 0 ; xy 3 2 5 7 9 / 4h2 15,42 5 0 12 ,29 1 1,87 ; xy 4 2'' 1 8 9'' / 4h2 15,42 11,6 7,8 12 ,29 1 0,67 . Касательные напряжения на контуре равны нулю: 131 xy 5 xy 6 xy 7 xy 8 xy 9 0 . По найденным значениям на рис. 45 построены эпюры напряжений x , y , xy . Заметим, что нормальные напряжения удовлетворяют условиям симметрии, а касательные напряжения являются кососимметричными. Кососимметричная функция в симметричных точках имеет противоположные по знаку значения. y 4.0 7.44 16 9.68 9.8 6.7 σ х , кПа σ х , кПа x 4.0 7.44 9.68 y 15.28 9.6 9.6 σ у , кПа σ х , кПа 16.84 3.44 3.44 17.96 x y 1.87 1.87 0.67 τ ху , кПа σ х , кПа 1.87 1.87 Рис. 45 132 x Анализируя распределение нормальных напряжений отметим, что они выравниваются по мере удаления от краев пластинки. Особенно это заметно на эпюре x . Так, на краю x 0 разность напряжений составляет 16 4 12 кПа, а к середине пластинки уменьшается до 9 ,68 5,8 3,88 кПа. Это явление отвечает известному принципу Сен-Венана. В соответствии с ним эффект действия самоуравновешенной системы сил уменьшается по мере удаления от места ее приложения. 3. Критерии оценки РГЗ Студент получает максимальную оценку за РГЗ (10 %), если задание выполнено в отведенный срок, с использованием компьютерной техники, аккуратно оформлено и содержит анализ полученных результатов. В случае выполнения задания без использования компьютера или задержки выполнения на 1 неделю (с использованием компьютера) студент получает 90 % от максимальной оценки (9 %). При выполнении РГЗ без использования компьютера и задержки выполнения на 1 неделю студент получает 80 % от максимальной оценки (8 %). Если РГЗ выполнено с опоздание более 1 недели студент получает 60 % от максимальной оценки (6 %). 133 Список литературы 1. Л.М.Шутенко, В.П.Пустовойтов, М.А.Засядько. Механіка споруд. – Харків, ХДАМГ, 2001. – 234 с. 2. Самуль В.И. Основы теории упругости и пластичности. – М.: Высш. школа, 1982. – 264 с. 3. В.Г.Рекач. Руководство к решению задач теории упру гости. – М.: Высш. школа, 1977. – 216 с. 4. Методичні вказівки і завдання до самостійної роботи з виконання розрахунково-графічного завдання із спецкурсу опору матеріалів «Основи теорії пружності» «Метод скінченних різниць у плоскій задачі теорії пружності». – Харків: ХНАМГ, 2007. – 24 с. 134

