Расчет балки
advertisement
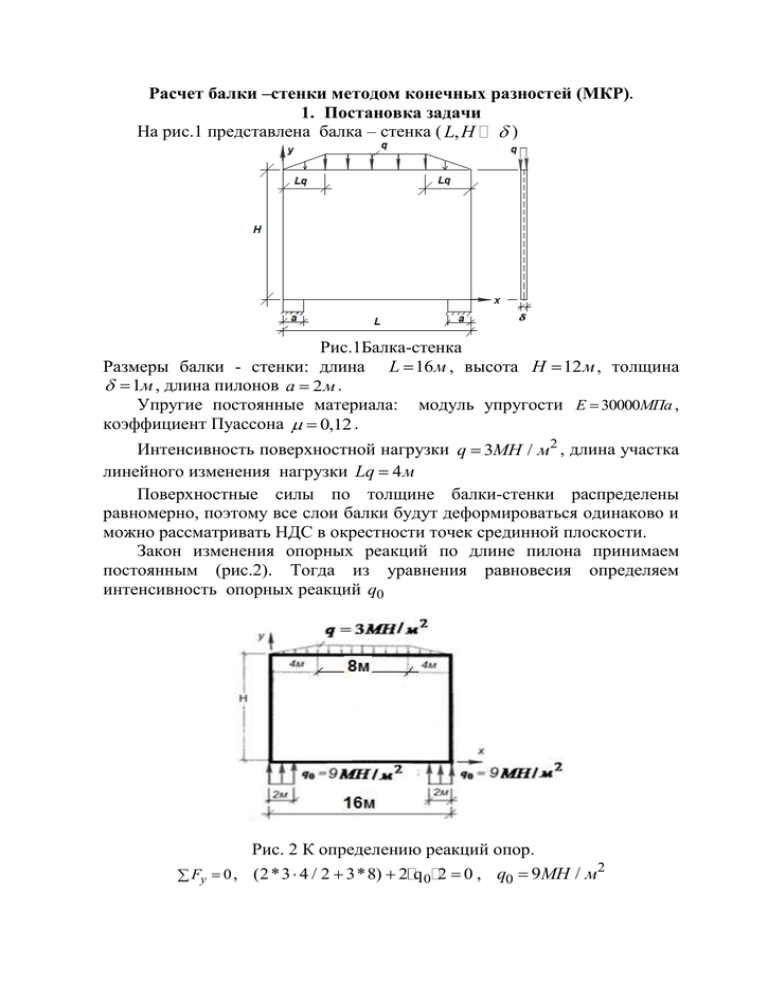
Расчет балки –стенки методом конечных разностей (МКР). 1. Постановка задачи На рис.1 представлена балка – стенка ( L, H ) Рис.1Балка-стенка Размеры балки - стенки: длина L 16 м , высота H 12 м , толщина 1м , длина пилонов a 2 м . Упругие постоянные материала: модуль упругости E 30000МПа , коэффициент Пуассона 0,12 . Интенсивность поверхностной нагрузки q 3МН / м2 , длина участка линейного изменения нагрузки Lq 4 м Поверхностные силы по толщине балки-стенки распределены равномерно, поэтому все слои балки будут деформироваться одинаково и можно рассматривать НДС в окрестности точек срединной плоскости. Закон изменения опорных реакций по длине пилона принимаем постоянным (рис.2). Тогда из уравнения равновесия определяем интенсивность опорных реакций q0 Рис. 2 К определению реакций опор. 2 Fy 0 , (2 *3 4 / 2 3*8) 2 q 0 2 0 , q0 9МН / м Уравнение совместности деформаций для функции напряжений ( x, y) в операторной форме имеет вид 2 2 2 (x, y) 2 ( x, y) (1) )( ) 0, x 2 y 2 x 2 y 2 или в традиционной форме (2) 4 (x, y) 4 ( x, y) 4 ( x, y) . 2 0 x 4 x 2y 2 y 4 Уравнение (2) необходимо решать с учетом условий на контуре балки-стенки. Для задания этих условий используют «рамную аналогию». Рассмотрим стержневую систему, очертание которой совпадает с контуром балки-стенки (рис.3). Интенсивность поверхностных сил по толщине балки-стенки не меняется, поэтому в стержневой системе переходим к погонным нагрузкам, собирая их по толщине торцов ( 1м ). Стержневая система находится в равновесии под действием заданной нагрузки и реактивных сил (рис.3). На рис. 7 показана эпюра изгибающих моментов, а на рис.8 эпюра продольных сил. ( Рис. 3 Рама с нагрузкой Рис. 5 К построению эпюры N Рис.4 Эпюра М, верхний ригель Рис.6 Эпюра М, нижний ригель Рис.7 Эпюра М изгибающих Рис. 8 Эпюра N продольных сил в моментов в раме раме В соответствии с рамной аналогией функция напряжений в точках контура равна изгибающему моменту в раме, а производная от функции по нормали к контуру равна продольной силе. Первая группа условий имеет вид: (0, y) M 01(y) 0 , (L, y) M 3 2 (y) 0 , (3) (x,0) M 03 (x) , (x,H) M1 2 (x) . Вторая группа условий запишется так: (0, y) N01(y) 9 , (L, y) N3 2 (y) 9 , x x (4) (0, x) N03 (x) 0 , (H, x) N12 (x) 0 . y y Таким образом, необходимо найти функцию напряжений ( x, y) удовлетворяющую дифференциальному уравнению (2) и условиям на контуре (3),(4). 2. Метод конечных разностей (МКР) Приведем формулы численного дифференцирования для вычисления первой и второй производных функции f ( x) в точке xi : (5) f( x h) f( xi h) f ( xi ) i 0(h 2 ) , 2h f( x h) 2 f( xi ) f( xi h) f ( xi ) i 0(h 2 ) . (6) 2 h Формулы (5), (6) являются приближенными и имеют второй порядок точности по h . Здесь h радиус окрестности точки xi . Покажем, как практически пользоваться данными формулами. Рассмотрим функцию f ( x) x3 и вычислим 1-ю и 2-ю производные в точке xi =1, используя формулы (5),(6). Отступим от точки xi влево и вправо на величину h 0.1 (рис.9) Рис. 9 Шаблон для вычисления производных Вычислим первую производную f( xi h) f( xi h) 1,13 0,93 f ( xi ) 3,01 . Точное 2h 2 0,1 производной f (x) 3 x 2 , f (1) 3 , следовательно, значение погрешность формулы (5) порядка h 2 0,01 . Вычислим вторую производную f( xi h) 2 f( xi ) f( xi h) 0,93 2 13 1,13 Точное f ( xi ) 6. h2 0,12 значение второй производной f (x) 6 x , f (1) 6 , т.е. результат вычислений по формуле (6) совпал с точным значением. Покажем, как использовать формулы (5),(6) при вычислении частных производных функции двух переменных в точке ( xi , y j ) . ( xi h x , y j ) ( xi h x , y j ) . ( xi , y j ) x 2h x ( xi , y j h y ) ( xi , y j h y ) ( xi , y j ) . y 2h y 2 ( xi h x , y j ) 2 ( xi , y j ) ( xi h x , y j ) x h x2 ( xi , y j h y ) 2 ( xi , y j ) ( xi , y j h y ) ( xi , y j ) 2 2 ( xi , y j ) 2 (7) (8) . . y h y2 Формулы (7)-(10) записаны на шаблоне точек (рис.10). В формулах (7)-(10) введем обозначения : xi 1 xi h x , xi 1 xi h x , y j 1 y j h y , y j 1 y j h y (9) (10) (11) Рис.10 Шаблон для вычисления частных производных Сучетом обозначений (11) формулы (7)-(10) запишутся так: ( xi 1, y j ) ( xi 1, y j ) . ( xi , y j ) x 2h x ( xi , y j 1) ( xi , y j 1) ( xi , y j ) . y 2h y 2 ( xi 1, y j ) 2 ( xi , y j ) ( xi 1, y j ) x h x2 ( xi , y j 1) 2 ( xi , y j ) ( xi , y j 1) ( xi , y j ) 2 2 (12) . ( xi , y j ) y 2 h y2 Опустим аргументы, оставим только индексы, ( xi , y j ) i , j , ( xi 1, y j ) i 1, j , ( xi 1, y j ) i 1, j , ( xi , y j 1) i , j 1 , ( xi , y j 1) i , j 1 (13) в результате формулы можно записать в более компактном виде: i 1, j i 1, j i , j 1 i , j 1 i , j , i, j y 2h y x 2h x 2 i 1, j 2 i , j i 1, j x h x2 i , j 1 2 i , j i , j 1 , 2 i j 2 , i , j y 2 h y2 Формулы (14) записаны в соответствии с шаблоном (рис.12) (14) Рис.12 Индексный шаблон 3. Конечно-разностная аппроксимация уравнения совместности деформаций и условий на контуре. На прямоугольной области наведем сетку (рис.13). Вдоль оси x L 16 область разобьем на 8 отрезков с шагом hx 2 м , а вдоль оси y на 8 8 H 12 6 с шагом hy 2 м . Таким образом, получим равномерную сетку, 6 6 так как hx h y h 2 м (рис.13). Дифференциальное уравнение (1) запишем в произвольной внутренней точке области ( xi , y j ) ( 2 2 )( 2i , j 2i , j ) 0,(i 1..7; j 1..5) x y x y Вторые частные производные заменим по формулам (14) ( 2 x 2 2 2 2 1 y h2 )[ 2 2 2 (i 1, j i 1, j 4 i 1, j i, j 1 i, j 1)] 0, (15) (16) (i 1..7; j 1..5) В квадратных скобках в формуле (16) записан конечно-разностный оператор Лапласа. Если к каждому из 5 слагаемых применить конечноразностный оператор Лапласа (сдвигая индексы), то в результате получим Неизвестные, входящие в уравнение (17) показаны на шаблоне (рис.14) Рис.13 Дискретизация срединной плоскости балки – стенки Рис. 14 Шаблон конечно-разностного уравнения в точке ( xi , y j ) Все 35 уравнений во внутренних точках области представлены ниже: [ ( 2 0, 08 0, 12 0, 28 1, 020 1, 18 1, 22 2, 08 2, 12 2, 21, 33, 1 1, -1-1, 1 ) h 40, ( 2 1, 08 1, 12 1, 28 2, 020 2, 18 2, 22 3, 0 8 3, 12 3, 22, 34, 12, -10, 1 ) h 40, ( 2 2, 08 2, 12 2, 2 8 3, 020 3, 18 3, 22 4, 08 4, 12 4, 23, 35, 13, -11, 1 ) h4 0, ( 2 3, 08 3, 12 3, 28 4, 020 4, 18 4, 22 5, 08 5, 12 5, 2 4, 36, 14, -12, 1 ) h 40, ( 2 4, 08 4, 12 4, 28 5, 020 5, 1 8 5, 22 6, 08 6, 12 6, 25, 37, 15, -13, 1 ) h 40, ( 2 5, 0 8 5, 12 5, 28 6, 020 6, 18 6, 22 7, 08 7, 12 7, 26, 38, 1 6, -14, 1 ) h 40, ( 2 6, 08 6, 12 6, 28 7, 020 7, 18 7, 22 8, 0 8 8, 12 8, 27, 39, 17, -15, 1 ) h 40, ( 2 0, 18 0, 22 0, 3 8 1, 120 1, 28 1, 32 2, 18 2, 22 2, 31, 43, 21, 0-1, 2 ) h4 0, ( 2 1, 18 1, 22 1, 38 2, 120 2, 28 2, 32 3, 18 3, 22 3, 3 2, 44, 22, 00, 2 ) h 40, ( 2 2, 18 2, 22 2, 38 3, 120 3, 2 8 3, 32 4, 18 4, 22 4, 33, 45, 23, 01, 2 ) h 40, ( 2 3, 1 8 3, 22 3, 38 4, 120 4, 28 4, 32 5, 18 5, 22 5, 34, 46, 2 4, 02, 2 ) h 40, ( 2 4, 18 4, 22 4, 38 5, 120 5, 28 5, 32 6, 1 8 6, 22 6, 35, 47, 25, 03, 2 ) h 40, ( 2 5, 18 5, 22 5, 3 8 6, 120 6, 28 6, 32 7, 18 7, 22 7, 36, 48, 26, 04, 2 ) h 4 0, ( 2 6, 18 6, 22 6, 38 7, 120 7, 28 7, 32 8, 18 8, 22 8, 3 7, 49, 27, 05, 2 ) h 40, ( 2 0, 28 0, 32 0, 48 1, 220 1, 3 8 1, 42 2, 28 2, 32 2, 41, 53, 31, 1-1, 3 ) h 40, ( 2 1, 2 8 1, 32 1, 48 2, 220 2, 38 2, 42 3, 28 3, 32 3, 42, 54, 3 2, 10, 3 ) h 40, ( 2 2, 28 2, 32 2, 48 3, 220 3, 38 3, 42 4, 2 8 4, 32 4, 43, 55, 33, 11, 3 ) h 40, ( 2 3, 28 3, 32 3, 4 8 4, 220 4, 38 4, 42 5, 28 5, 32 5, 44, 56, 34, 12, 3 ) h 4 0, ( 2 4, 28 4, 32 4, 48 5, 220 5, 38 5, 42 6, 28 6, 32 6, 4 5, 57, 35, 13, 3 ) h 40, ( 2 5, 28 5, 32 5, 48 6, 220 6, 3 8 6, 42 7, 28 7, 32 7, 46, 58, 36, 14, 3 ) h 40, ( 2 6, 2 8 6, 32 6, 48 7, 220 7, 38 7, 42 8, 28 8, 32 8, 47, 59, 3 7, 15, 3 ) h 40, ( 2 0, 38 0, 42 0, 58 1, 320 1, 48 1, 52 2, 3 8 2, 42 2, 51, 63, 41, 2-1, 4 ) h 40, ( 2 1, 38 1, 42 1, 5 8 2, 320 2, 48 2, 52 3, 38 3, 42 3, 52, 64, 42, 20, 4 ) h4 0, ( 2 2, 38 2, 42 2, 58 3, 320 3, 48 3, 52 4, 38 4, 42 4, 5 3, 65, 43, 21, 4 ) h 40, ( 2 3, 38 3, 42 3, 58 4, 320 4, 4 8 4, 52 5, 38 5, 42 5, 54, 66, 44, 22, 4 ) h 40, ( 2 4, 3 8 4, 42 4, 58 5, 320 5, 48 5, 52 6, 38 6, 42 6, 55, 67, 4 5, 23, 4 ) h 40, ( 2 5, 38 5, 42 5, 58 6, 320 6, 48 6, 52 7, 3 8 7, 42 7, 56, 68, 46, 24, 4 ) h 40, ( 2 6, 38 6, 42 6, 5 8 7, 320 7, 48 7, 52 8, 38 8, 42 8, 57, 69, 47, 25, 4 ) h 4 0, ( 2 0, 48 0, 52 0, 68 1, 420 1, 58 1, 62 2, 48 2, 52 2, 6 1, 73, 51, 3-1, 5 ) h 40, ( 2 1, 48 1, 52 1, 68 2, 420 2, 5 8 2, 62 3, 48 3, 52 3, 62, 74, 52, 30, 5 ) h 40, ( 2 2, 4 8 2, 52 2, 68 3, 420 3, 58 3, 62 4, 48 4, 52 4, 63, 75, 5 3, 31, 5 ) h 40, ( 2 3, 48 3, 52 3, 68 4, 420 4, 58 4, 62 5, 4 8 5, 52 5, 64, 76, 54, 32, 5 ) h 40, ( 2 4, 48 4, 52 4, 6 8 5, 420 5, 58 5, 62 6, 48 6, 52 6, 65, 77, 55, 33, 5 ) h 4 0, ( 2 5, 48 5, 52 5, 68 6, 420 6, 58 6, 62 7, 48 7, 52 7, 6 6, 78, 56, 34, 5 ) h 40, ( 2 6, 48 6, 52 6, 68 7, 420 7, 5 8 7, 62 8, 48 8, 52 8, 67, 79, 57, 35, 5 ) h 40 ] Заметим, что уравнения, записанные в точках сетки вблизи контура, содержат неизвестные в законтурных точках. Например, в точке ( x1, y1) ( 2 0, 08 0, 12 0, 28 1, 020 1, 18 1, 22 2, 08 2, 12 2, 21, 33, 1 1, -1-1, 1 ) h 40 Неизвестные в законтурных точках исключаем в уравнениях, используя условия на контуре (см.(4)) (0, y) N01(y) 9 , (L, y) N3 2 (y) 9 , x x (0, x) N03 (x) 0 , (H, x) N12 (x) 0 . y y Например, на левой кромке контура 1 откуда находим 0, j (1, j 1, j ) N01(y j ) 9 , x 2h 1, j 2h(1, j 9) , т.е. значения функции в законтурных точках выражаются через значения функции во внутренних точках. Значения функции в точках контура задаются с учетом условий на контуре (см.(3)) (0, y) M 01(y) 0 , (L, y) M 3 2 (y) 0 , (x,0) M 03 (x) , (x,H) M1 2 (x) . Например, на кромке 0-1 и на кромке 1-2 0, j M 0 1 (y j ) 0 , i,6 M12 (xi ) . Таким образом, выполнен переход от дифференциального уравнения в частных производных (2) с условиями на контуре (3),(4) к системе линейных алгебраических уравнений (СЛАУ) относительно неизвестных значений функции во внутренних узлах сетки i , j . Получаемое решение СЛАУ является приближенным и при уменьшении шага сетки h 0 сходится к точному (при этом число уравнений возрастает ). На рис.15 показан портрет матрицы СЛАУ. Рис. 15 Портрет матрицы системы уравнений Матрица системы симметричная и имеет разряженную ленточную структуру с числом неизвестных в типовом уравнении равным 13. На рис.16 показана функция напряжений, полученная в результате решения СЛАУ. На рис.17,18,19 представлены эпюры нормальных и касательных 2 2 2 напряжений: x 2 , y 2 , xy , вычисленные с помощью xy y x соответствующих конечно-разностных формул (14). Рис. 16 Функция напряжений. Лицевой и торцевой контуры есть очертание эпюр моментов в ригелях рамы. Углы наклона левой и правой кромок равны продольной силе в стойках Рис. 17 Напряжения x Рис.18 Напряжения y Рис.19 Напряжения x y Рис.20 Главное напряжение max Рис. 21 Главное напряжение min Рис. 22 Эквивалентное (приведенное) напряжение i max min На рис. 20, 21 представлены эпюры главных напряжений max , min . Для балки-стенки из хрупкого материала можно проверить прочность по первой теории прочности 1 max R , 3 min R . На рис.22 представлены эпюры эквивалентных напряжений по 3-ей теории прочности (материал пластичный). На рис.23 для балки стенки, загруженной сосредоточенной силой показано векторное поле главных напряжений (половина балки) Рис.23 Векторное поле главных напряжений По направлению максимальных главных напряжений (растягивающих) выполняется армирование железобетонной балки (рис.24) Рис.4.13 Рис.24 Траектории главных напряжений при изгибе и схема армирования железобетонной балки.