Т.Н. ГОЛОВАНОВА, А.М. ШТЕРЕНБЕРГ
СБОРНИК ЗАДАЧ ПО ФИЗИКЕ
И ПРИМЕРЫ ИХ РЕШЕНИЯ
ЧАСТЬ Ι
Самара
Самарский государственный технический университет
2016
0
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
К а ф е д р а «Общая физика и физика нефтегазовых производств»
Т.Н. ГОЛОВАНОВА, А.М. ШТЕРЕНБЕРГ
СБОРНИК ЗАДАЧ ПО ФИЗИКЕ
И ПРИМЕРЫ ИХ РЕШЕНИЯ
ЧАСТЬ Ι
Самара
Самарский государственный технический университет
2016
1
Печатается по решению редакционно-издательского совета СамГТУ
УДК 53(076.1)
ББК 22.3я73
Г 61
Голованова Т.Н.
Г 61 Сборник задач по физике и примеры их решения. В 2 ч., Ч. Ι /
Т.Н. Голованова, А.М. Штеренберг. – Самара: Самар. гос. техн. ун-т, 2016. –
84 с.: ил.
Содержит основные законы и формулы, необходимые для решения задач.
Даны примеры решения типовых задач и задачи для самостоятельного решения. Пособие предназначено для студентов-заочников инженерно-технических
специальностей вузов. Может быть использовано студентами дневных отделений вузов.
УДК 53(076.1)
ББК 22.3я73
Г 61
Р е ц е н з е н т : канд. физ.-матем. наук, доцент М.Р. Виноградова
© Т.Н. Голованова, А.М. Штеренберг, 2016
© Самарский государственный
технический университет, 2016
2
ПРЕДИСЛОВИЕ
Сборник содержит основные законы и формулы, необходимые
для решения задач. Даны примеры решения типовых задач и задачи
для самостоятельного решения. Числовые данные приведены с учетом точности соответствующих величин и правил действия над приближенными числами.
Учебное пособие предназначено для оказания помощи студентамзаочникам инженерно-технических специальностей вузов при изучении
курса общей физики. Может быть полезным для студентов дневных отделений вузов. Пособие составлено в соответствии с действующей программой по курсу физики для технических университетов.
Даны две таблицы вариантов контрольных работ по механике
(контрольная работа № 1) и молекулярной физике с термодинамикой
и электростатикой (контрольная работа № 2). Таблицы содержат варианты для специальностей, учебными планами которых предусмотрено четыре контрольных работы по курсу физики. Кроме того в пособии даны методические указания к решению задач и выполнению
контрольных работ, а также справочные материалы.
3
ПРОГРАММА КУРСА ФИЗИКИ
ДЛЯ ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ
ЗАОЧНОГО ОТДЕЛЕНИЯ ВУЗА
ЧАСТЬ Ι
МЕХАНИКА
Скорость и ускорение материальной точки. Тангенциальное и
нормальное ускорения. Угловая скорость и угловое ускорение. Законы Ньютона. Силы в механике. Закон сохранения импульса. Работа и
кинетическая энергия. Консервативные силы. Потенциальная энергия, ее связь с работой и консервативной силой. Закон сохранения
механической энергии. Момент силы и момент импульса. Закон сохранения момента импульса.
Момент инерции твердого тела. Теорема Штейнера. Уравнение
динамики вращения твердого тела. Кинетическая энергия вращающегося твердого тела. Принцип относительности Галилея. Постулаты
специальной теории относительности (СТО). Преобразования Лоренца. Следствия из преобразований Лоренца. Релятивистский импульс.
Основное уравнение релятивистской динамики. Энергия в СТО.
Взаимосвязь массы и энергии.
Виды механических колебаний. Свободные незатухающие колебания. Сложение гармонических колебаний. Свободные затухающие колебания. Логарифмический декремент. Вынужденные колебания. Механические волны. Характеристики волн. Уравнение плоской волны.
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Основное уравнение молекулярно-кинетической теории. Средняя
энергия молекул. Температура. Уравнение состояния идеального газа.
Закон равномерного распределения энергии по степеням свободы.
Распределения Максвелла и Больцмана. Скорости молекул. Барометрическая формула. Средняя длина свободного пробега молекул. Явления переноса. Диффузия, теплопроводность и вязкость. Работа газа.
4
Внутренняя энергия и количество теплоты. Первое начало термодинамики. Теплоемкость идеального газа. Адиабатический процесс. Тепловые двигатели. Цикл Карно. Второе начало термодинамики. Энтропия. Закон возрастания энтропии.
ЭЛЕКТРОСТАТИКА
Электрический заряд. Закон Кулона. Напряженность электрического поля. Поток напряженности. Теорема Гаусса для электрического поля в вакууме. Расчет электрических полей с помощью теоремы
Гаусса. Потенциал электрического поля. Связь между напряженностью и потенциалом электрического поля. Электрический диполь.
Диэлектрики. Поляризация диэлектриков. Свободные и связанные заряды. Электрическое смещение. Расчет электрических полей в диэлектриках. Проводники в электрическом поле. Электроемкость.
Конденсаторы. Энергия заряженного проводника и конденсатора.
Энергия электрического поля.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Савельев И.В. Курс общей физики: кн. 1: Механика: учеб. пособие / И.В.
Савельев. – М.: Астрель, 2004. – 336 с.: ил.
2. Савельев И.В. Курс общей физики: кн. 2: Электричество и магнетизм:
учеб. пособие / И.В. Савельев. – М.: Астрель, 2004. – 254 с. ил.
3. Иродов И.Е. Механика. Основные законы: учеб. пособие / И.Е. Иродов.
– М.: Лаборатория знаний, 2005. – 309 с.: ил.
4. Иродов И.Е. Физика макросистем. Основные законы: учеб. пособие /
И.Е. Иродов. – М.: Лаборатория знаний, 2004. – 207 с.: ил.
5. Детлаф А.А., Яворский Б.М. Курс физики: учеб. пособие / А.А. Детлаф,
Б.М. Яворский. – М.: Академия, 2003. – 720 с.: ил.
6. Волькенштейн В.С. Сборник задач по общему курсу физики. Изд. 3-е,
испр. и доп. – СПб.: Книжный мир, 2005. – 328 с.
5
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Решение задач. Систематическое решение задач обычно проводится по следующей схеме.
1. Сделать анализ условия задачи и записать числовые данные,
переведя их при необходимости в одну систему единиц.
2. Определить, какие законы и формулы лежат в основе решения
данной задачи, дать словесную формулировку этих законов, разъяснить буквенные обозначения формул. Если при решении задачи используется формула, не выражающая какой-либо физический закон,
то эту формулу следует вывести.
3. При необходимости выполнить рисунок, поясняющий содержание задачи. Аккуратно выполненный рисунок поможет не только
лучше понять условие задачи, но и выбрать необходимое для решения задачи уравнение.
4. Решение задач сопровождается краткими, но исчерпывающими
пояснениями, раскрывающими физический смысл формул.
5. Все задачи надо решать в общем виде, т. е. выразить искомую
величину в буквенных обозначениях величин, заданных в условии
задачи. При таком решении не производятся вычисления промежуточных величин, следовательно уменьшается вероятность возможных
ошибок. Решение в общем виде позволяет также провести анализ полученного результата.
6. Для проверки правильности полученного решения необходимо
в формулу, выражающую искомую величину, подставить единицы
величин, заданных в условии задачи, и убедиться в том, что полученная единица соответствует искомой величине. Если такого соответствия нет, то задача решена неверно.
7. Выразить числовые значения величин, заданных в условии задачи, в одной системе единиц (преимущественно в СИ) и выписать их
для наглядности столбиком. Подставить эти значения в окончательную формулу, выражающую искомую величину, и получить числовой ответ. При этом следует учесть точность числовых данных и на
правила действий с приближенными числами. В числовом ответе ос6
тавляется столько значащих цифр, сколько их содержится в числовом
данном задачи, содержащем наименьшее число этих цифр. Числовой
ответ следует записывать в виде произведения десятичной дроби с
одной значащей цифрой перед запятой на соответствующую степень
десяти. Например, вместо 3250 нужно записать 3,250·103 .
Выполнение контрольных работ. При выполнении контрольных работ необходимо руководствоваться следующим.
1. Номера задач определяются по таблице вариантов. Номер варианта соответствует последней цифре в шифре студента.
2. Контрольная работа выполняется в обычной школьной тетради,
на обложке которой приводятся сведения по следующему образцу:
Контрольная работа № 1
по физике
студента электротехнического факультета СамГТУ
Андреева А.П.
Шифр 201061
Адрес: г. Самара, ул. Тополей 4, кв. 5.
3. Условия задач записываются полностью без сокращений. Для
замечаний преподавателя на страницах тетради оставляются поля.
4. В конце контрольной работы нужно указать учебное пособие,
используемое при изучении физики (название пособия, автор, год издания). Это необходимо для того, чтобы рецензент мог указать студенту, что следует изучить для завершения контрольной работы.
5. Высылать одновременно на рецензию нужно не более одной
работы.
6. Если контрольная работа не зачтена, то студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения
которых оказались неверными.
7. Зачтенная работа предъявляется экзаменатору. Студент во
время экзамена должен дать пояснения по существу решения задач,
входящих в контрольную работу.
7
КОНТРОЛЬНАЯ РАБОТА № 1
МЕХАНИКА
Основные формулы
Кинематика
1. Средняя скорость и среднее ускорение материальной точки
∆r
∆v
,
⟨v ⟩ = , ⟨a ⟩ =
(1Ф)
∆t
∆t
где ∆r, ∆v − перемещение точки и приращение скорости за время ∆t;
− радиус-вектор точки.
Используется также средняя скорость, равная отношению пройденного пути s ко времени t, за которое этот путь был пройден
v = s.
(2Ф)
t
2. Модули скорости и ускорения
ds ,
dv d 2 s ,
v=
a=
=
(3Ф)
dt
dt dt 2
где s – путь, пройденный материальной точкой.
3. Проекции скорости и ускорения на координатные оси
dx
dy
dz
vx = , vy = , vz = .
(4Ф)
dt
dt
dt
d 2y ,
d 2x ,
d 2z .
ах = 2 a y = 2 а z = 2
(5Ф)
dt
dt
dt
4. Модули скорости и ускорения через их проекции на координатные оси
v=
v2x + v2y + v2z , a =
a2x + a2y + a2z .
(6Ф)
5. Координата точки и проекция скорости на выбранную ось координат при равноускоренном движении
ax t 2
, vx = v0x + ax t,
x = x0 + v0x t +
(7Ф)
2
где 0 , v0x − начальная координата и проекция начальной скорости.
8
6. Тангенциальное и нормальное ускорения при криволинейном
движении
dv ,
v2 ,
a =
an =
(8Ф)
dt
где – радиус кривизны траектории в данной точке, или радиус окружности.
7. Модули угловой скорости и углового ускорения точки, движущейся по окружности,
dφ
dω
, β=
,
ω=
(9Ф)
dt
dt
где φ − угол поворота радиус-вектора точки.
8. Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности,
(10Ф)
v = ω, a = β, an = ω2 ,
где v − линейная скорость;
R – радиус окружности.
9. Полное ускорение точки, движущейся по окружности,
a=a
2
+ a n 2 = β 2 + ω4 .
(11Ф)
Динамика
10. Второй закон Ньютона
d
dv
=
= m = ma,
(12Ф)
dt
dt
где − равнодействующая сила, действующая на тело (материальную точку) массой m;
= mv – импульс тела;
v – его скорость;
а – ускорение тела.
11. Третий закон Ньютона
1 = − 2 .
(13Ф)
Силы, с которыми взаимодействуют два тела, равны по модулю и
противоположны по направлению, имеют одинаковую природу и
приложены к разным телам.
9
12. Силы в механике:
а) гравитационная сила (закон всемирного тяготения)
m1 m2
(14Ф)
=G 2 ,
где G – гравитационная постоянная (находится из таблицы);
m1 , m2 – массы взаимодействующих тел;
R – расстояние между телами (тела рассматриваются как материальные точки или однородные шары);
б) сила упругости ( закон Гука)
x = − kx,
(15Ф)
где x – проекция силы упругости на ось Х;
– коэффициент упругости (жесткость в случае пружины);
x – проекция перемещения конца пружины или стержня при деформации. Знак «минус» означает, что проекции силы упругости и
перемещения конца пружины (стержня) имеют противоположные
знаки;
в) сила трения скольжения
(16Ф)
тр = µN,
где µ – коэффициент трения скольжения, зависит от природы и состояния трущихся поверхностей;
N – сила нормального давления.
Законы сохранения
13. Закон сохранения импульса
= const.
(17Ф)
Импульс замкнутой системы тел (или частиц) остается постоянным, т. е. не меняется со временем. Для двух тел (i = 2)
m1 v1 + m2 v2 = m1 u1 + m2 u2 ,
(18Ф)
где v1 , v2 – скорости тел до взаимодействия;
u1 , u2 – скорости тел после взаимодействия.
14. Работа, совершаемая силой F при перемещении частицы из
точки 1 в точку 2,
10
A = ∫ Fd s = ∫ Fds cosα .
2
1
2
(19Ф)
1
где s – элементарное перемещение частицы;
α − угол между перемещением s и силой .
15. Кинетическая энергия частицы
mv!
P2 .
=
(20Ф)
2
2m
16. Связь кинетической энергии с работой
А = ∆Ек = Ек2 – Ек1,
(21Ф)
где A – работа всех сил, действующих на частицу;
∆ к – приращение кинетической энергии частицы;
Ек1, Ек2 – кинетическая энергия частицы в моменты времени t1 и
t2 . Выражение (21Ф) обобщается на механическую систему: работа
всех сил (внутренних и внешних) равна приращению кинетической
энергии системы.
17. Потенциальная энергия:
а) упруго деформированной пружины
к=
=
kx2
;
(22Ф)
п
2
б) тела, находящегося в однородном поле силы тяжести
(23Ф)
Еп = mgh,
где h – высота тела над уровнем, принятым за нулевой. Формула
справедлива при h ≪ R, где R – радиус Земли.
18. Связь потенциальной энергии с работой консервативных сил
# = п1 − п2 ,
(24Ф)
где Eп1 , Eп2 – потенциальная энергия в точках 1 и 2 консервативного
поля (например, поля тяжести Земли). Для механической системы под
Eп1 , Eп1 следует понимать потенциальную энергию системы в двух ее
положениях или конфигурациях (начальном Eп1 и конечном Eп1 ).
19. Закон сохранения энергии
E = Eк + Eп = const.
(25Ф)
Полная механическая энергия E системы, находящейся под действием консервативных сил, сохраняется с течением времени.
11
Динамика твердого тела
20. Моменты инерции тел массой m относительно оси, проходящей через их центр масс:
а) обруча (и тонкостенного цилиндра) радиуса R относительно
оси, перпендикулярной плоскости обруча (или оси цилиндра),
I = m 2 ;
(26Ф)
б) диска (и сплошного цилиндра) радиуса R относительно оси,
перпендикулярной плоскости диска (или оси цилиндра),
m 2
I=
;
(27Ф)
2
в) стержня длиной l относительно оси, нормальной стержню,
21. Теорема Штейнера
ml 2
.
I=
12
(28Ф)
I = IС + ma2 .
(29Ф)
Момент инерции тела I относительно произвольной оси равен
сумме момента инерции $С относительно оси, параллельной данной и
проходящей через центр масс тела, и произведению массы тела m на
квадрат расстояния a между осями.
22. Момент импульса тела относительно неподвижной оси вращения Z
%Z = IωZ ,
(30Ф)
где ωZ – проекция угловой скорости тела на ось Z.
23. Закон сохранения момента импульса тела и системы тел
IωZ = const.
(31Ф)
Для системы тел: I – суммарный момент инерции системы; ωZ –
проекция угловой скорости на ось Z.
24. Уравнение динамики твердого тела, вращающегося вокруг
неподвижной оси Z,
IβZ = &Z ,
(32Ф)
где βZ – проекция углового ускорения на ось Z;
&Z – результирующий момент внешних сил относительно оси Z.
12
25. Кинетическая энергия твердого тела, вращающегося вокруг
неподвижной оси,
Iω2
.
(33Ф)
к =
2
26. Кинетическая энергия при плоском движении твердого тела
IС ω2 mv2С
,
+
(34Ф)
к =
2
2
где IС – момент инерции тела относительно оси, проходящей через
его центр масс;
vС – скорость центра масс.
Механические колебания
27. Дифференциальное уравнение свободных незатухающих гармонических колебаний частицы
d 2x
+ ω2 x = 0,
2
dt
где x – смещение частицы от положения равновесия;
ω – циклическая частота свободных колебаний.
28. Период колебаний физического маятника
' = 2π(
I
,
mgl
(35Ф)
(36Ф)
где I – момент инерции маятника относительно неподвижной горизонтальной оси (оси качания);
m – масса маятника;
g – ускорение свободного падения;
l – расстояние от точки подвеса до центра масс маятника.
29. Период колебаний тела массой m под действием квазиупругой
силы
' = 2π
m,
где k – коэффициент упругости (жесткость пружины).
13
(37Ф)
30. Приведенная длина физического маятника, равная длине математического маятника, имеющего такой же период, что и физический
I
lпр = .
(38Ф)
ml
31. Кинематическое уравнение гармонических колебаний
(39Ф)
x = A cos ( ωt + φ0 ) ,
где х – смещение точки, равное ее координате в момент времени t;
А – амплитуда колебаний;
ω – циклическая частота;
ωt + φ0 – фаза колебаний;
φ0 – начальная фаза.
32. Амплитуда A и начальная фаза φ результирующего колебания
при сложении двух колебаний одного направления и одинаковой частоты:
#=
A21 + A22 + 2A1 A2 cos(φ2 − φ1 ),
где #1 , #2 – амплитуды складываемых колебаний;
φ1 , φ2 – начальные фазы колебаний;
A1 sinφ1 + A2 sinφ2
.
φ = arctg
A1 cosφ1 + A2 cosφ2
(40Ф)
(41Ф)
Специальная теория относительности
33. Линейные размеры тела (длина стержня), движущегося относительно инерциальной системы отсчета (ИСО) со скоростью v,
* = *0 1 − v2 ⁄+ 2 ,
(42Ф)
где l0 – собственные размеры тела, или собственная длина стержня;
c – скорость света в вакууме.
Из (42Ф) видно, что линейные размеры тела уменьшаются в направлении его движения.
34. Собственный интервал времени, измеренный по часам, движущимся вместе с телом,
∆τ = ∆t1 − v2 ⁄+ 2 ,
14
(43Ф)
где ∆t – интервал времени, измеренный по часам в ИСО, относительно которой тело движется со скоростью v. Из (43Ф) видно ∆τ < ∆t.
Это означает, что движущиеся часы идут медленнее, чем неподвижные, т. е. существует эффект замедления хода движущихся часов.
35. Релятивистское выражение для импульса тела, движущегося
со скоростью v относительно ИСО,
mv
,
=
(44Ф)
2
2
1 − v ⁄ +
где m – масса тела, постоянная во всех ИСО, т. е. не зависящая от
скорости тела. При v ≪ c релятивистский импульс переходит в классическое выражение = mv.
36. Энергия покоя тела
2
(45Ф)
0 = mc .
37. Кинетическая энергия тела
mc2
− mc2 .
(46Ф)
к =
2
2
1 − v ⁄ c
38. Полная энергия тела
m+ 2
.
(47Ф)
=
2
2
1 − v ⁄ c
39. Связь между импульсом и кинетической энергией тела
1
P = c Eк ( Eк + 2mc 2 ) .
(48Ф)
Из этого соотношения при Eк << mc2 получается формула
P = 2mEк , которая используется в механике Ньютона.
Примеры решения задач
Пример 1. Автомобиль проехал расстояние между двумя городами за некоторое время. Половину этого времени он шел со скоростью v1 . В оставшееся время половину пути он шел со скоростью v2 ,
и другую половину – со скоростью v3 . Найти среднюю скорость автомобиля на всем пути между городами.
15
v1 ,
v2 ,
v3 .
⟨v ⟩ = ?
A
Решение
s2
s1
s3
t1
v1
t3
v3
t2
v2
B
Рис. 1
Изобразим траекторию прямолинейного движения автомобиля и
отложим на ней пути s1 , s2 , s3 , проходимые автомобилем за время t1 ,
t2 , t3 соответственно со скоростью v1 , v2 , v3 (см. рис. 1). Средняя скорость автомобиля на всем пути s находится по формуле (2Ф)
s0 + s2 + s1
,
⟨v ⟩ =
(1)
t1 + t2 + t3
где
s0 = v1 t1 , s2 = v2 t2 , s3 = v3 t3 .
(2)
По условию задачи s2 = s3 , или с учетом (2)
v 2 t2 = v 3 t3 .
(3)
Из условия задачи видно также
t1 = t2 + t3 .
(4)
Тогда (1) запишется как
s1 + 2 s2
.
⟨v ⟩ =
(5)
2t1
Пройденные пути s1 и s2 берутся из уравнений (2). С учетом (4)
путь s2 = v2 (t1 – t3), где t3 = s3/v3 (см. (2)). Учитывая s3 = s2, получим:
Откуда
s2 = v2 (t1 – s2/v3).
s2 =
v 2 t1
.
1+ v2 ⁄v1
Учитывая это выражение и путь s0 из уравнений (2), находим из
(5) искомую среднюю скорость:
v1
v2 v3
.
⟨v ⟩ = +
2 v2 + v3
16
Пример 2. Жонглер бросил вертикально вверх мячик. Когда мячик достиг верхней точки своего подъема hм = 4,9 м, жонглер бросил
вверх второй мячик с той же начальной скоростью v0 . На какой высоте встретятся тела?
Решение
hм = 4,9 м.
h=?
Y
С
hм
h
Рис. 2
v0
0
Воспользуемся формулой координаты при равноускоренном
движении (см. (7Ф), где x = y). Время отсчитывается с момента броска второго тела. В этот момент начальная координата первого тела y0
= hм (рис. 2). Проекция ускорения свободного падения на ось Y будет
отрицательной,
так как ускорение g направлено против оси Y. С
учетом этого, координаты первого и второго тел запишутся следующим образом:
gt2
,
y1 = hм −
(1)
2
gt2
.
(2)
y2 = v0 t −
2
Из уравнений (7Ф) при x = y найдем начальную скорость второго
тела v0 = 2ghм . Подставляя это выражение в (2), получим:
g t2 .
y2 = 2ghм t −
(3)
2
В момент встречи (t = t0 ) имеем: y1 = y2 , откуда, учитывая (1) и
(3), найдем время, через которое тела встретятся
t1 = hм ⁄2g .
17
(4)
При t = t1 координата y1 = h. Тогда из (1) найдем
gt21
.
h = hм −
2
Подставляя сюда (4), получим искомую высоту:
3
h = hм = 3,7 м.
4
Тот же результат получится, если использовать координату (3).
Пример 3. Из одной точки одновременно бросили два тела под
углами α1 = 60° и α2 = 45° к горизонту с начальными скоростями
v1 = 40 м/с и v2 = 50 м/с . Траектории тел лежат в одной плоскости
(рис. 3). На каком расстоянии l друг от друга будут находиться тела
через время t = 3,0 с ?
Решение
α1 = 60°,
Y
v1 = 40 м/с,
y1
α2 = 45°,
v2 = 50 м/с,
y2
0
B
l
A
С
hmax1
x1
t = 3,0 с .
;1
ℎmax2
1
2
<
x2
s2
Рис. 3
l=?
В отсутствие сопротивления воздуха движение тел
является свободным падением, происходящим по параболе. На рис. 3 показаны примерные траектории движения тел и их
положение через заданное время (точки А и В). Искомое расстояние
между телами l = АВ = = АС 2 + ВС 2 , или через координаты тел
(точек)
*=
(x2 − x1 )2 + 8y2 − y1 9 .
2
18
(1)
Используя формулу координаты для заданных движений (см.
(7Ф)), найдем:
x1 = v1 t cosα1 , x2 = v2 t cosα2 ,
g= 2
g= 2
.
y1 = v1 t sinα0 −
, y2 = v2 t sinα! −
2
2
Подставляя эти координаты в (1) и, используя формулу из тригонометрии
cos(α0 − α! ) = sinα0 sinα! + cosα0 cosα! ,
получим:
* = t v02 + v22 − 2v1 v2 cos(α1 – α 2 ).
Учитывая числовые данные, найдем: l = 30
м. Интересно отметить, что квадратный корень
в выражении (2) представляет собой модуль
относительной скорости vотн тел (см. рис. 4). В
этом легко убедиться, применяя теорему косинусов к треугольнику скоростей
vотн =
(2)
v@
vотн
v2
α0 α!
v21 + v22 − 2v1 v2 cos(α1 – α2 ).
Рис. 4
(3)
Видно, что vотн не зависит от времени, т. е. при движении скорость одного тела относительно другого по модулю остается постоянной. Тогда, учитывая (3), расстояние между телами можно выразить через относительную скорость: l = vотн t.
Пример 4. Тело вращается вокруг неподвижной оси по закону
φ = A + Bt + Ct2 , где A = 10 рад, B = 20 рад/с, C = – 2,0 рад/с2 . Найти
полное ускорение точки, находящейся на расстоянии R = 0,10 м от
оси вращения, для момента времени t = 4,0 с.
19
Решение
φ = A + Bt + Ct2 ,
A = 10 рад,
aD
an
B = 20 рад/с,
a
C = −2,0 рад/с2 ,
R = 0,10 м,
Рис. 5
t = 4,0 с.
Полное ускорение a точки, движущейся по
окружности, равно геометрической сумме тангена=?
циального ускорения a , направленного по касательной к траектории, и нормального ускорения
an , направленного к центру окружности (рис. 5)
a = a + an .
Так как векторы a и an взаимно перпендикулярны, то модуль ускорения (см. (11Ф))
C = a τ 2 + a n 2 .
(1)
Модули тангенциального и нормального ускорений точки вращающегося тела выражаются формулами
aτ = βR, an = ω2 R,
(2)
где β, ω – модули углового ускорения и угловой скорости. Подставляя выражения (2) в формулу (1), получим:
C = Rβ2 + ω4 .
(3)
Угловую скорость ω найдем, взяв первую производную угла поворота по времени (см. условие задачи). Тогда в момент времени
t = 4,0 с модуль угловой скорости
ω = dφ/dt = B + 2Ct = 4,0 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой
скорости по времени,
β = dω/dt = 2C = − 4,0 рад/с2 .
20
Подставляя числовые значения ω, β и R в формулу (3), найдем:
a = 1,6 м/с2 .
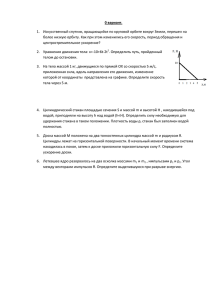
Пример 5. На тело массой m, лежащее на гладкой горизонтальной плоскости, в момент времени t0 = 0 начала действовать сила, зависящая от времени, F = kt, где k – постоянная величина. Направление этой силы все время составляет угол α с горизонтом (см. рис. 6).
Найти: а) скорость тела в момент отрыва от плоскости; б) путь, пройденный телом к этому моменту.
Решение
m,
F = kt,
α.
v1 , ;0 = ?
Y
F
N
α
m 0
X
mg
Рис. 6
На тело действуют: сила F; сила тяжести mg и сила реакции N
(рис. 6). Сила трения отсутствует, так как поверхность гладкая. Под
действием этих сил тело движется с ускорением а = dv/dt вдоль оси
X. Применим второй закон Ньютона (см. (12Ф))
mC = + mE + F,
(1)
или в проекциях на оси X, Y
v
= ktcosα,
(2)
m
t
ktsinα + F − mg = 0.
(3)
Учли условие задачи F = kt. Из уравнения (2) имеем
kt
v = cosα ∙ t.
m
После интегрирования получим скорость тела
kt2
v=
cosα.
(4)
2m
21
В момент отрыва от плоскости N = 0, и из уравнения (3) находим
время отрыва
mg
.
t1 =
(5)
ksinα
Подставляя это время в (4), найдем скорость тела в момент отрыва от плоскости:
mg2 cosα
.
v1 =
2
2ksin α
Путь, пройденный телом s = ∫ vdt (см. (3Ф), первая формула).
Учитывая (4), запишем:
kt3 cosα
kcosα
2
.
H t t =
;=
6m
2m
Подставляя сюда время отрыва (5), найдем путь, пройденный телом к моменту отрыва от плоскости:
m3 g3 cosα
;1 = 2 3 .
6k sin α
Пример 6. Частица массой m в момент t = 0 начинает двигаться
под действием силы = 0 sinωt, где 0 и ω – постоянные величины.
Найти путь, пройденный частицей, в зависимости от времени t.
Решение
Используем второй закон Ньютона (12Ф)
m,
dv
= 0 sinωt.
m = .
t
s(t) = ?
Учитывая условие задачи, запишем:
0
dv = sinω.dt.
m
После интегрирования в пределах от 0 до t получим
0
v=
(1 − cosωt).
mω
Путь, пройденный частицей за время t (см. (3Ф)),
L
; = H vdt.
0
22
(1)
Подставим в эту формулу выражение (1) в скалярном виде
L
0
H(1 − cosωt) dt.
;=
mω
0
Выполняя интегрирование в указанных пределах, найдем путь
0
(ωt − sinωt).
;=
mω2
Пример 7. Искусственный спутник Земли имеет круговую орбиту, удаленную от поверхности Земли на расстояние h = 260 км. Определить период обращения спутника Т относительно центра Земли.
Радиус Земли R = 6,4∙ 103 км.
Решение
На искусственный спутник Земли (ИЗС) дейстh = 2,60·105 м,
вует только сила притяжения (тяготения) к Земле
6
R = 6,4·10 м. (силой тяготения со стороны Луны и Солнца пренебрегаем), которая сообщает спутнику нормальное
'=?
(центростремительное) ускорение (см. (8Ф), вторая
формула)
v2 ,
(1)
Cn =
R+h
где v – скорость спутника относительно центра Земли;
+ h – радиус круговой орбиты спутника.
Применим второй закон Ньютона для ИЗС
(2)
mCn = т ,
где m – масса спутника;
т – сила тяготения, определяется законом всемирного тяготения
(14Ф). Для данной задачи
mM
,
т = G
(3)
(R + h)2
где G – гравитационная постоянная;
M – масса Земли.
23
Учитывая (1) и (3), из второго закона Ньютона (2) найдем:
GM .
v2 =
R+ h
(4)
Применяя второй закон Ньютона (12Ф) к свободно падающему телу, находящемуся у поверхности Земли (h = 0), получим с учетом (3):
M
g=G 2.
(5)
R
Поделив (4) на (5), найдем скорость ИЗС
g
.
v=R
(6)
R+h
Полагая движение спутника по круговой орбите равномерным,
запишем (см. (2Ф)):
2π(R + h)
.
v=
(7)
'
Из (6) и (7) найдем период обращения спутника
'=
2π(R + h) R + h
.
(
g
R
Если положить ускорение свободного падения g = 9,8 м/с2 , то
получим T = 90 мин.
Пример 8. Лодка массой m стоит неподвижно на поверхности
озера. На корме и на носу лодки на расстоянии l друг от друга сидят
два рыбака массами m1 и m2 . Для улучшения клева рыбаки меняются
местами. В какую сторону и на какое расстояние переместится лодка?
Решение
Система «лодка − рыбаки» не является замкнутой, так
m,
как на нее действуют внешние силы: сила тяжести и сила
m1 ,
Архимеда. Эти силы уравновешивают друг друга, а сила
трения лодки о воду пренебрежимо мала по сравнению с сиm2 ,
лами взаимодействия рыбаков с лодкой (внутренние силы).
l.
Поэтому можно применить закон сохранения импульса
(17Ф). Импульс системы до начала движения рыбаков равен
s=?
24
нулю. Следовательно, после начала движения суммарный импульс
также равен нулю
mv + m1 v1 + m2 v2 = 0,
(1)
где v, v1 , v2 – скорости лодки и рыбаков
относительно воды. Допустим, m1 > m2
и лодка движется в направлении перемещения рыбака с меньшей массой m2
(см. рис. 7, где цифрами 1 и 2 обозначены положения рыбаков после перемещения лодки). Тогда равенство (1) в
проекциях на ось X запишется
Из рис. 7 видно
m1
2
v
1
v1
v2
m2
m
s
l
X
mv − m1 v1 + m2 v2 = 0.
l−s
l+s
s
v = t , v1 = t , v2 = t ,
Рис. 7
(2)
(3)
где s – модуль перемещения лодки;
t – время движения лодки и рыбаков, которое одинаково для всех
тел. Подставляя (3) в (2), найдем:
(m1 − m2 )*
.
m + m1 + m2
При условии m1 < m2 и для выбранного направления оси X имеем
s=
(m2 − m1 )l
.
m + m1 + m2
Полученные решения можно объединить в одну формулу, если
ввести проекцию перемещения лодки на ось Х
s=
(m1 − m2 )l
.
sx =
m + m1 + m2
При m1 > m2 проекция sP > 0 и лодка перемещается влево. При
m1 < m2 , sP < 0 и лодка перемещается в противоположную сторону.
25
Пример 9. Снаряд массой m = 10,0 кг летит горизонтально со
скоростью v = 200 м/с и разрывается на две части (осколки). Одна
часть массой m1 = 3,00 кг полетела вперед под углом α = 60° к горизонту со скоростью v1 = 400 м/с. С какой скоростью и в каком направлении полетела вторая часть снаряда?
Решение
m = 10,0 кг,
m1 = 3,00 кг,
v = 200 м/с,
v1 = 400 м/с,
α = 60°.
m1 R1
Y
m1 v1S
α
β
0
m2 v2S
v2 = ?
mR
X
m2 R2
Рис. 8
Система «снаряд − осколки» не является замкнуβ=?
той, так как на тела системы действует сила тяжести.
Если рассматривать суммарный импульс осколков сразу
после разрыва, то он будет равен импульсу снаряда непосредственно до
разрыва. Это следует из того, что за время разрыва снаряда импульсы
осколков практически не изменяются. Таким образом, к нашей системе можно применить закон сохранения импульса (см. (18Ф))
mv = m1 v1 + m2 v2 .
(1)
Здесь mv – импульс снаряда до разрыва;
m1 v1 , m2 v2 – импульсы осколков.
Импульсы осколков и снаряда показаны на рис. 8 в соответствии
с законом сохранения импульса системы «снаряд – осколки». Спроектируем (1) на оси координат (см. рис. 8)
mv = m1 v1 cosα + m2 v2 cosβ,
(2)
m1 v1 sinα − m2 v2 sinβ = 0,
26
(3)
где β – искомый угол, под которым полетела к горизонту вторая часть
снаряда, находится из уравнений (2) и (3)
tgβ =
m1 v1 sinα
.
mv − m1 v1 cosα
(4)
Скорость второй части находим из уравнения (3)
v2 =
m1 v1 sinα
.
m2 sinβ
(5)
Подставляя числовые данные задачи в (4) найдем: β = 36,6°. Тогда из формулы (5) найдем v2 = 250 м/с.
Задачу можно решить также с использованием теоремы косинусов. Из рис. 8 видно
m2 v2 = (mv)2 + (m1 v1 )2 − 2mm1 vv1 cosα,
откуда находим v2 . Угол β находим также из теоремы косинусов
откуда
(m1 v1 )2 = (mv)2 + (m2 v2 )2 − 2mm2 vv2 cosβ,
(mv)2 + (m2 v2 )2 − (m1 v1 )2
.
cosβ =
2mm2 vv2
При этом закон сохранения импульса (1) используется при построении треугольников, к которым применялась теорема косинусов.
Пример 10. Тело массой m соскальзывает без трения по наклонному желобу, переходящему в окружность. Тело соскальзывает с
наименьшей высоты, необходимой для совершения полного оборота.
Найти силу давления на желоб в точке А, радиус-вектор которой составляет угол α с вертикалью. Из полученного решения определить
силу давления тела на желоб в верхней В и нижней С точках петли.
27
Решение
Искомая сила давления А по третьему закону Ньютона
равна по модулю силе нормальной реакции N (см. рис. 9)
m,
А = N.
(1)
Величина N находится из второго закона Ньютона
(12Ф), записанного в проекциях на ось X для тела, находящегося в точке А (см. рис. 9),
α.
А = ?
В = ?
С = ?
mv2
,
N +mgcosα =
R
(2)
где v – скорость тела в точке А;
R – радиус окружности, по которой движется тело;
v2/R – нормальное ускорение тела в точке А.
D m
vВ
В
mg α
О
X
R
hmin
v
N
mg
А
h
С
Рис. 9
В системе «тело − Земля» отсутствуют силы трения и сопротивления, следовательно можно использовать закон сохранения энергии
(25Ф). В точке D тело обладает потенциальной энергией (23Ф)
E1 = Eп = mghmin ,
(3)
28
где hmin – наименьшая высота, необходимая для совершения полного
оборота. В точке А полная энергия тела состоит из потенциальной
(см. (23Ф)) и кинетической (20Ф) энергии
mv2
,
2 = mgh +
2
где h = R(1 + cosα) (см. рис. 9). Тогда
mv2
.
(4)
2 = mgR(1 + cosα) +
2
По закону сохранения энергии 1 = 2 , или, учитывая (3) и (4),
получим:
mv2
.
mghmin = mgR(1 + cosα) +
(5)
2
Тело скатывается с наименьшей высоты hmin , необходимой для
совершения полного оборота. Следовательно, в наивысшей точке
траектории (точка В, рис. 9) на тело действует только сила тяжести
(состояние невесомости). Применим второй закон Ньютона в этой
точке
mv2В
,
mg =
(6)
R
и закон сохранения энергии для положений тела в точках D и В
mv2В
.
(7)
mghmin = 2mgR +
2
Из (6) и (7) получим
5
hmin = R.
2
Подставив (8) в (5), получим:
v2 = gR(3 − 2cosα).
Из уравнений (2) и (9) с учетом (1) найдем искомое давление
(8)
(9)
А = 3mg(1 − cosα).
(10)
Угол α отсчитывается от вертикали по часовой стрелке. Следовательно, в верхней точке петли (точка В) α = 0 и В = 0. (см. (10)).
Этот результат мы ранее использовали при нахождении (6) и получи29
ли его из физических соображений (тело скатывается с минимальной
высоты hmin , необходимой для совершения полного оборота). Для
нижней точки петли (точка С) угол α = 180°, тогда из (10) следует
С = 6mg.
Пример 11. Тело массой M лежит на вершине гладкой полусферы радиуса R. В тело попадает пуля массой m, летящая горизонтально
со скоростью v, и застревает в нем. Пренебрегая смещением тела во
время удара, найти высоту h, на которой оно оторвется от поверхности полусферы. Высота отсчитывается от основания полусферы. При
какой скорости пули vx тело сразу оторвется от полусферы?
Решение
Полусфера гладкая, поэтому в системе «тело − Земля»
M,
сила трения отсутствует. Сила сопротивления воздуха также
m,
не учитывается. Следовательно, можно использовать закон
сохранения энергии (25Ф). Полная энергия 1 тела вместе с
R,
пулей сразу после удара равна энергии 2 тела с пулей в моv.
мент отрыва от полусферы. Энергия 1 находится в точке 1
h = ? на вершине полусферы (см. рис. 10)
(m + М)v21
.
(1)
1 = (m + М)gR +
2
Здесь v1 – скорость тела с пулей
v1
сразу после удара пули. Энергия 2
находится в точке 2 в момент отрыва
2
от полусферы (см. рис. 10)
vx = ?
m
v М
1
h
α
О
R
(m+М)g
v2
2
(m + М)v22
, (2)
= (m + М)gh +
2
где v2 – скорость в момент отрыва
Рис.10
от полусферы. По закону сохранения энергии E1 = E2 , или, учитывая уравнения (1) и (2), получим:
v22
v21
(3)
gR + = gh + ,
2
2
X
30
Скорость v1 найдем из закона сохранения импульса (17Ф)
mv = (m + М)v1 .
(4)
Откуда скорость тела вместе с пулей
mv
.
(5)
v1 =
m+М
Необходимо заметить, что кинетическая энергия пули mv2 ⁄2 не
равна кинетической энергии тела с застрявшей в нем пулей
(m + М)v21 ⁄2 сразу после удара. Это объясняется тем, что в системе
«пуля − тело» во время удара (время движения пули в теле) действует сила трения, работа которой приводит к уменьшению (диссипации)
кинетической энергии системы. Для определения скорости v2 применим второй закон Ньютона в точке 2 в проекциях на ось X (рис. 10)
(m + М)v22
,
(m + М)gcosα =
R
где cosα = h⁄R. Тогда из (6)
v2 = gh,
(6)
(7)
откуда видно, что на бóльшей высоте h тело отрывается с бóльшей
скоростью. Подставим выражения (5), (7) в (3) и из полученного равенства найдем искомую высоту
2
m2 v 2
h=
2 + 3 R.
3g(m + М)
Для определения скорости пули vx , при которой тело сразу отрывается от полусферы, воспользуемся законом сохранения импульса в
проекциях на горизонтальное направление
mvx = (m + М)u,
(8)
где u – скорость тела вместе с пулей в момент отрыва от полусферы.
Скорость u найдем из второго закона Ньютона. При этом учтем, что
на тело действует только сила тяжести (состояние невесомости).
(m + М)u2
.
(m + М)g =
R
31
(9)
Из (8) и (9) получим скорость пули, при которой тело сразу отрывается от полусферы
М
vx = W1 + m X gR.
Пример 12. Через блок в виде сплошного диска, имеющего массу
m = 80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1 = 100 г и m2 = 200 г. Определить ускорение, с
которым будут двигаться грузы. Трением и массой нити пренебречь.
Решение
Рассмотрим силы, действующие на грузы и на блок.
m = 80 г,
На каждый груз действуют две силы: сила тяжести m1 g
m1 = 100 г, и m g и сила упругости (сила натяжения нити) Т и Т
1
2
2
m2 = 200 г. (см. рис. 11). Направим ось X для каждого груза в направлении его ускорения a и запишем для них второй
a=?
закон Ньютона (12Ф) в проекциях на эти оси
T1 − m1 g = m1 a,
(1)
m2 g − T2 = m2 a.
(2)
Z
R
X
a
TY1
TY2
T1
T2
X
m1 g
m2 g
Рис. 11
На блок действуют силы натяжения нитей TY1 и TY2 (см. рис. 11).
Согласно третьему закону Ньютона (13Ф), с учетом невесомости нити, модули этих сил равны соответствующим модулям сил натяжения, действующим на грузы,
(3)
T1Y = T1 , T2Y = T2 .
32
Под действием моментов сил натяжения TY1 и TY2 относительно
оси Z, перпендикулярной плоскости рисунка и направленной от нас
(крестик на рисунке), блок приобретает угловое ускорение β. Модуль
этого ускорения (см. (10Ф)) β = a ⁄R, где a – тангенциальное ускорение точек блока, находящихся на расстоянии R от его оси (R – радиус блока). При отсутствии проскальзывания нити по блоку a = a,
и модуль углового ускорения
a
β= .
(4)
R
Запишем уравнение динамики твердого тела для блока (32Ф)
M2z − M1z = Iβz ,
(5)
где M1z , M2z – моменты сил натяжения нити относительно оси Z, равные проекциям соответствующих моментов M1 и M2 относительно
точки, лежащей на оси вращения, совпадающей с осью Z;
I – момент инерции блока относительно оси вращения;
βz – проекция углового ускорения.
Уравнение (5) записано с учетом знаков проекций (правило правого винта). Поэтому проекции равны модулям соответствующих величин. Используем формулу модуля момента силы М = Fd. У нас F –
сила натяжения нитей T1Y и T2Y ; d – плечо силы, равное радиусу диска
R. Тогда моменты, входящие в уравнение (5), запишутся следующим
образом:
(6)
M1z = T1Y R; M2z = T2Y R; βz = β.
С учетом формулы момента инерции блока (сплошного диска)
I = mR /2 и равенств (3), (4) и (6), уравнение (5) примет вид:
2
T2 − T1 =
ma
.
2
(7)
Выражая силы натяжения T1 и T2 из равенств (1) и (2) и подставляя их в уравнение (7), получим искомое ускорение грузов:
a=
2(m2 − m1 )g
= 2,9 м/с2 .
2(m1 + m2 ) + m
33
Z
I1
\1
\2
I2
−\2
Рис. 12
Пример 13. Два горизонтальных диска свободно
вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны I1 и I2 , а угловые скорости – ω1 и
ω2 . После падения верхнего диска на нижний оба
диска, благодаря трению между ними, начали через
некоторое время вращаться как единое целое. Найти:
а) установившуюся угловую скорость вращения дисков; б) работу, которую совершили при этом силы
трения.
Решение
На диски действуют внешние моменты сил тяжести и реакции
опор. Относительно вертикальной оси вращения Z сумма моментов
этих сил равна нулю. Следовательно, к данной системе тел
I1 , I2 ,
можно применить закон сохранения момента импульса.
\1 , \2 .
Сумма моментов импульса двух дисков L1 + L2 , вращаю\ = ? щихся отдельно друг от друга, равна моменту импульса
дисков L, вращающихся как единое целое
Aтр = ?
L1 + L2 = L.
(1)
С учетом формулы момента импульса L = Iω и свойства аддитивности момента инерции I = I1 + I2, закон сохранения момента импульса (1) запишется следующим образом:
I1 [1 + I2 [2 = (I1 + I2 )ω,
откуда искомая угловая скорость
I1 ω1 + I! ω!
.
ω=
(2)
I1 + I!
Если диски в начальный момент времени вращались в одну сторону, то проекция угловой скорости на ось Z (см. рис. 12)
ωz =
I1 ω1 + I! ω!
,
I1 + I!
34
если в разные стороны, то
I 1 ω1 − I ! ω!
.
I1 + I!
Работа сил трения равна приращению кинетической энергии системы
(3)
Aтр = к2 − к1 .
Кинетическая энергия системы до падения верхнего диска на
нижний к1 и после паления к2 соответственно равны
ωz =
I1 ω21 I2 ω22
,
+
(4)
к0 =
2
2
Iω2
.
(5)
к! =
2
С учетом свойства аддитивности I = I1 + I2 и формулы (2), имеем:
(I1 ω1 + I2 ω2 )2
.
(6)
к! =
2(I1 + I2 )
Подставляя (4) и (6) в формулу (3), найдем работу сил трения:
I1 I2 (ω1 − ω2 )2
.
Aтр = −
2(I1 + I2 )
Знак «минус» означает, что силы трения уменьшают кинетическую энергию дисков (диссипация энергии), т. е. работа сил трения
отрицательная.
Пример 14. Найти кинематическое уравнение гармонических колебаний точки, если максимальное ускорение amax = 50 см/с2 , период
колебаний Т = 2 с и смещение в начальный момент времени x0 = 5 см.
Решение
Запишем кинематическое уравнение гармониamax = 50 см/с2 ,
ческих колебаний точки (см. (39Ф))
Т = 2 с,
х = Acos(ωt + φ0 ).
(1)
Проекция ускорения на ось X равна второй проx0 = 5 см.
изводной от координаты x по времени (см. (5Ф))
x(t) = ?
ax = −Aω2 cos(ωt + φ0 ),
35
откуда видно, что максимальное ускорение
amax = Aω2 .
Учитывая
2π
ω= ,
Т
найдем из (2) амплитуду колебаний:
(2)
(3)
amax Т 2
.
A=
(4)
2
4π
Начальная фаза φ0 находится из (1) при t = 0
x0 = Acosφ0 ,
откуда с учетом (4)
4π2 x0
.
φ0 = arccos
(5)
2
amax Т
Используя (3) − (5), запишем уравнение гармонических колебаний точки (1) через данные задачи:
amax Т 2
2π
4π2 x0
.
хx =
cos _ t + arccos
2`
4π2
Т
amax Т
Учитывая числовые данные задачи, получим искомое уравнение
с числовыми коэффициентами:
х = 5 cosπt (см).
Пример 15. Частица, движущаяся со скоростью v = 0,99 с (с –
скорость света в вакууме) в неподвижной системе отсчета K, пролетела от места своего рождения до точки распада расстояние l = 3,0
км. Определить собственное время жизни частицы τ.
Решение
Используем относительность времени в
v = 0,99 с,
специальной теории относительности (СТО)
τ
с = 3.108 м/с,
t= _
,
(1)
2
2
1 v /c
3
l = 3,0 км = 3,0∙ 10 м. где t – время, измеренное по часам, находяτ=?
щимся в неподвижной системе отсчета K
(лабораторная система);
36
τ – собственное время (в задаче – собственное время жизни частицы), измеряющееся по часам, движущимся вместе с частицей, с которой связана подвижная система отсчета K Y . Учитывая, что t = l/v,
найдем из (1) собственное время жизни частицы
l
v2
τ = v (1 − 2 = 1,4 мкс.
+
(2)
Пример 16. Какую работу надо совершить, чтобы увеличить скорость частицы массой m = 1,0 кг от v1 = 0,60с до v2 = 0,80с
8
(с = 3,0.10 м/с – скорость света в вакууме)? Сравнить полученный
результат со значением, вычисленным по нерелятивистской формуле.
Решение
m = 1,0 кг,
Искомая работа равна приращению кинетической
v1 = 0,60 с, энергии частицы
(1)
A = Eк2 − Eк1 .
v2 = 0,80 с.
Скорость частицы сравнима со скоростью света, поэтому надо использовать релятивистскую формулу
AР = ?
(46Ф)
A=?
mc2
Eк =
− mc2 .
1 − v2 ⁄+ 2
С учетом этой формулы работа (1) запишется следующим образом:
Ар = mc 2
1
1
−
1 − v2 / c 2
1 − v12 / c 2
2
После вычислений получим
.
AР = 3,8.10 Дж.
Если использовать нерелятивистскую формулу кинетической энергии Eк = mv2 ⁄2, то получим величину работы в три раза меньшую
mv22 mv21
16
A=
−
= 1,3.10 Дж.
2
2
16
37
ТАБЛИЦА ВАРИАНТОВ К КОНТРОЛЬНОЙ РАБОТЕ № 1
Таблица содержит варианты для специальностей, учебными планами которых предусмотрено четыре контрольных работы.
Вариант
0
1
2
3
4
5
6
7
8
9
1
101
102
103
104
105
106
107
108
109
110
2
111
112
113
114
115
116
117
118
119
120
Номера задач
3
4
121
131
122
132
123
133
124
134
125
135
126
136
127
137
128
138
129
139
130
140
5
141
142
143
144
145
146
147
148
149
150
6
151
152
153
154
155
156
157
158
159
160
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
101. Теплоход идет по реке от одного пункта до другого со скоростью v0 = 12 км/ч относительно берега, а обратно – со скоростью
v! = 20 км/ч. Найти среднюю скорость теплохода относительно берега и скорость течения реки. Скорость теплохода относительно воды
считать постоянной.
102. Автомобиль прошел половину пути со скоростью v0 . На остальной части пути он половину времени двигался со скоростью v1 , а
оставшийся участок – со скоростью v2 . Найти среднюю скорость за
все время движения автомобиля.
103. Вертикально вверх с интервалом времени τ брошены два
шарика с одинаковой скоростью v0 из одной и той же точки. Через
какое время после броска второго шарика они столкнутся?
38
104. Под каким углом к горизонту необходимо бросить тело, чтобы: а) центр кривизны вершины его траектории находился на земной
поверхности; б) радиус кривизны начала его траектории был в η = 8,0
раза больше, чем в вершине?
105. Частица движется в плоскости ХY по закону x = αt,
y = αt (1– βt), где α и β – положительные постоянные. Найти: а) уравнение траектории частицы y(x); б) скорость v и ускорение a в зависимости от времени t.
106. Два тела бросили одновременно из одной точки: одно вертио
кально вверх, другое под углом α = 60 к горизонту. Начальная скорость каждого тела v0 = 25 м/с. Найти расстояние между телами через время t = 1,7 с.
о
107. Тело бросили под углом α = 30 к горизонту со скоростью
va = 30 м/с. Найти нормальное an и тангенциальное Cτ ускорения через время t = 5 c после начала движения тела.
108. Две частицы движутся с ускорением свободного падения g в
однородном поле тяжести. В начальный момент времени частицы находились в одной точке и имели скорости v1 = 3,0 м/с и v2 = 4,0 м/с,
направленные горизонтально и в противоположные стороны. Найти
расстояние между частицами в момент времени, когда векторы их
скоростей окажутся взаимно перпендикулярными.
109. Твердое тело начинает вращаться вокруг неподвижной оси с
угловым ускорением β = αt, где α = 2,0·10–2 рад /с2 . Через, сколько
времени после начала вращения полное ускорение произвольной точки тела будет составлять угол φ = 60° с ее скоростью?
110. Колесо вращается вокруг неподвижной оси, при этом угол φ
его поворота зависит от времени как φ = β t2 , где β = 0,20 рад/с2 .
Найти полное ускорение a точки на ободе колеса в момент t = 2,5 с,
если скорость точки в этот момент v = 0,65 м/с.
111. На частицу действует сила F = 10ti + 3t2 j, где i, j – орты осей
Х, У. Найти импульс частицы в момент времени t = 2,0 с.
39
112. Аэростат массой m = 250 кг начал опускаться с ускорением
a = 0,20 м/с2 . Найти массу балласта, который надо сбросить за борт,
чтобы аэростат получил такое же ускорение, но направленное вертикально вверх. Сопротивление воздуха не учитывать.
113. В установке, показанной на рис.
m1
m2
13, массы тел равны m0 , m1 и m2 , массы
блока и нитей пренебрежимо малы. Трение
в блоке не учитывать. Найти ускорение a, с
которым опускается тело массой m0 , и силу
m0
натяжения нити, связывающей тела массаРис. 13
ми m1 и m2, если коэффициент трения между этими телами и горизонтальной поверхностью равен µ.
114. Небольшое тело движется снизу вверх по наклонной плоскости, составляющей угол α = 15° с горизонтом. Найти коэффициент
трения, если время подъема тела оказалось в η = 2,0 раза меньше
времени спуска.
115. Автомобиль едет по шоссе со скоростью v = 72 км/ч. Коэффициент трения между колесами автомобиля и дорогой µ = 0,30. За
какое минимальное время автомобиль сможет развернуться, не снижая скорости?
116. Велосипедист едет по круговой горизонтальной площадке
ра-диусом R. Коэффициент трения µ = µ0 (1– r⁄R ), где µ0 – постоянная величина; r – расстояние от велосипедиста до центра O площадки. Найти максимальный радиус окружности rmax с центром в точке
О, по которой велосипедист может ехать с максимальной скоростью.
Какова эта скорость?
117. На покоившуюся частицу массой m в момент t = 0 начала
действовать сила, зависящая от времени по закону F = bt (τ − t), где
b – постоянная величина, τ – время действия силы. Найти: а) импульс
частицы после окончания действия силы; б) путь, пройденный частицей за время действия силы.
40
118. К бруску массой m, лежащему на гладкой горизонтальной
плоскости, приложили постоянную по модулю силу F = mg/3. В процессе его прямолинейного движения угол α между направлением
этой силы и плоскостью изменяется по закону α = ks, где k – постоянная величина; s – пройденный бруском путь (из начального положения). Найти скорость бруска как функцию угла α.
119. Частица массой m в момент времени t = 0 начинает двигаться под действием силы F = F0 sin ωt, где F0 , ω – постоянные величины. Найти путь, пройденный частицей в зависимости от времени t.
120. В момент времени t = 0 частица массой m начинает двигаться под действием силы F = F0cosωt, где F0 и ω – постоянные величины. Сколько времени тело будет двигаться до первой остановки? Какой путь оно пройдет за это время?
121. Найти отношение кинетической энергии спутника планеты к
его потенциальной энергии. Спутник движется по круговой орбите.
122. Насколько переместится относительно воды лодка длиной
l = 3,5 м и массой m0 = 200 кг, если человек массой m! = 80 кг перешел с кормы на нос лодки?
123. Тело массой m1 = 2,0 кг упруго сталкивается с покоящимся
телом, при этом его скорость уменьшилась в n = 2 раза и изменилась
по направлению на угол α = 90°. Найти массу m2 второго тела.
124. Граната, летит горизонтально и разрывается на два осколка.
Скорость одного осколка v1 = 30 м/с и направлена под углом α = 30°
к горизонту. Скорость другого осколка v2 = 60 м/с и направлена вертикально вниз. Найти скорость гранаты до разрыва. Во сколько раз
масса одного осколка больше другого?
125. Человек массой M стоит на льду и толкает в горизонтальном
направлении санки массой m, сообщая им скорость v, при этом он откатывается назад. Какую работу совершает при этом человек?
126. Спортсмен массой m1 = 60 кг, стоя на коньках, бросает тело
массой m2 = 2,0 кг под углом α = 60° к горизонту со скоростью
41
v2 = 5,0 м/с. На какое расстояние откатится спортсмен после броска,
если коэффициент трения коньков о лед µ = 0,10? Перемещение
спортсмена во время броска не учитывать.
127. Какую работу надо совершить, чтобы тело массой m = 10 кг
втащить по наклонной плоскости высотой h = 1,5 м и основанием
a = 2,5 м. Коэффициент трения µ = 0,2.
128. Доска массой M равномерно движется по гладкой горизонтальной поверхности со скоростью v. Сверху на доску осторожно
кладут кирпич массой m. Какое расстояние пройдет кирпич по доске
за время его проскальзывания до остановки? Коэффициент трения
между кирпичом и доской равен µ.
129. Небольшое тело соскальзывает с высоты h = 8,0 м по наклонной плоскости, плавно переходящей в «мертвую петлю» радиусом
R = 4,0 м. На какой высоте, считая от нижней точки петли, тело оторвется от ее поверхности?
130. На тележку массой M, движущуюся по горизонтальной прямой с постоянной скоростью v, падает с высоты h кирпич массой m.
Кирпич остается на тележке. Найти количество теплоты Q, выделившейся при этом.
131. Свинцовая пуля массой m = 10 г летит горизонтально со ско-
ростью v = 100 м/с и попадает в деревянный брусок массой М = 1,0 кг,
подвешенный на длинной нити. Насколько увеличится температура пули, если η = 70 % выделенной теплоты идет на ее нагревание?
132. На сплошной однородный цилиндр радиусом R = 10 см и
массой m1 = 9,0 кг плотно намотана нить, к концу которой привязан
груз массой m2 = 2,0 кг (рис. 14). Найти угловое ускорение цилиндра.
133. Однородный сплошной цилиндр массой m = 8,0 кг и радиусом R = 1,3 см (рис. 15) в момент времени t = 0 начинает опускаться
под действием силы тяжести. Найти угловое ускорение β цилиндра.
42
m
m1
R
R
m2
Рис. 15
Рис. 14
134. В установке (рис. 16) известны масса сплошного однородного цилиндра m, его радиус R и массы тел m1 и m2 . Скольжение нити
по поверхности цилиндра и трение в его оси не учитывать. Найти угловое ускорение β цилиндра.
m
m1
R
1
m
2
m1
m2
m2
Рис. 16
Рис. 17
135. Сплошной однородный цилиндр массой m вращается под
действием сил натяжения нити, к концам которой подвешены грузы
массами m1 и m2 (рис. 16). Найти отношение сил натяжения '0 ⁄'!
вертикальных участков 1 и 2 нити в процессе движения. Убедиться,
что при m → 0 '0 = '! .
136. В системе, показанной на рис. 17, известны: массы тел m1 и
m2 , коэффициент трения µ между телом массой m1 и горизонтальной
плоскостью, а также масса блока m, который можно считать одно43
родным сплошным диском. Скольжение нити по блоку отсутствует. В
момент t = 0 тело массой m2 начинает опускаться. Пренебрегая массой нити и трением в оси блока, найти ускорение a тела массой m2 .
v
R
Рис. 18 7
Рис. 19
137. По горизонтальной плоскости катится диск (рис. 18) и, предоставленный самому себе, останавливается, пройдя расстояние
s = 16 м. Начальная скорость диска, v = 8 м/с. Найти коэффициент
трения.
138. Однородный цилиндр радиусом R раскрутили вокруг его оси
до угловой скорости ω0 и поместили в угол (рис. 19), коэффициент
трения между стенками угла и цилиндром равен µ. Сколько оборотов
n сделает цилиндр до остановки?
139. Тонкий однородный стержень длиной l из вертикального положения падает на горизонтальную поверхность. Найти линейные
скорости крайней и средней точек стержня в момент времени, когда
стержень займет горизонтальное положение.
140. Сколько времени будет скатываться без скольжения обруч с
наклонной плоскости длиной l = 2 м и высотой h = 10 см?
141. Человек массой m1 стоит на краю горизонтального однородного диска массой m2 и радиусом R. Диск может свободно вращаться
вокруг вертикальной оси, проходящей через его центр. В некоторый
момент человек начал двигаться по краю диска, совершил перемещение на угол ϕ′ относительно диска и остановился. Пренебрегая размерами человека, найти угол φ, на который повернется диск к моменту остановки человека.
142. Однородный шар скатывается без скольжения по наклонной
плоскости, составляющей угол α с горизонтом. Найти ускорение центра шара и коэффициент трения, при котором скольжения не будет.
44
143. Математический маятник длиной l = 1,5 м совершает гармонические колебания с амплитудой А = 10 см. Найти максимальную
скорость грузика маятника.
144. При перемещении математического маятника с Земли на
другую планету период его колебаний увеличился в n1 = 6 раз. Во
сколько раз масса Земли больше массы планеты, если радиус Земли в
n2 = 2 раза больше радиуса планеты?
145. Математический маятник, состоящий из шарика массой
m = 260 г и нити длиной l = 2,4 м, совершает гармонические колебания с амплитудой А = 10 см. Найти скорость шарика при прохождении положения равновесия и максимальное значение силы, под действием которой совершаются колебания.
146. Математический маятник длиной l0 = 40 см и тонкий однородный стержень длиной l = 60 см совершают синхронно гармонические колебания вокруг горизонтальной оси. Найти расстояние от центра стержня до этой оси.
147. Обруч диаметром D = 56 см висит на гвозде и совершает
гармонические колебания под действием силы тяжести. Найти период
колебаний обруча, принимая его за физический маятник.
148. На стержне длиной l0 = 60 см укреплены два одинаковых
грузика: один в середине стержня, другой – на конце. Стержень с грузиками колеблется около горизонтальной оси, проходящей через его
свободный конец. Найти приведенную длину и период гармонических колебаний данного маятника. Массой стержня пренебречь.
149. Частица совершает гармонические колебания с начальной
фазой α = 0. При смещении частицы от положения равновесия на
х1 = 4 см ее скорость v0 = 6 см/с, а при смещении на х2 = 3 см скорость v2 = 8 см/с. Определить циклическую частоту колебаний ω0.
150. Пружинный маятник вывели из положения равновесия и отпустили. Через какое время (в долях периода) кинетическая энергия
колеблющегося тела будет равна потенциальной энергии пружины?
Массу пружины не учитывать.
45
151. Шарик, подвешенный на пружине, отвели из положения равновесия вертикально вниз на расстояние х = 4,0 см и сообщили ему
скорость v0 = 1,0 м/с, после чего он стал совершать гармонические
колебания с частотой ω0 = 25 рад/с. Найти амплитуду колебаний.
152. Стержень движется в продольном направлении с постоянной
скоростью v относительно инерциальной К – системы отсчета. При
каком значении скорости длина стрежня в этой системе отсчета будет
на η = 0,5 % меньше его собственной длины ?
153. Имеется прямоугольный треугольник с катетом a = 5,0 м и
углом между этим катетом и гипотенузой α = 30°. Найти в системе
отсчета К ꞌ , движущейся относительно этого треугольника со скоростью v = 0,866 с вдоль катета a (с – скорость света в вакууме): а) соответствующее значение угла αY ; б) длину * Y гипотенузы и ее отношение к собственной длине *a .
154. Найти собственную длину стержня la , если в К – системе отсчета (лабораторная система) его длина l = 1,00 м, угол между стержо
нем и направлением движения α = 45 и скорость v = с/2, где с – скорость света в вакууме.
155. С какой скоростью двигались в К – системе отсчета часы,
если за время t = 5,0 с (в К – системе) они отстали от неподвижных
часов этой системы на ∆t = 0,10 с?
156. Собственное время жизни нестабильной частицы ∆t0 = 10
нс. Какой путь пролетит эта частица до распада в лабораторной системе отсчета, где ее время жизни ∆t = 20 нс?
157. В пунктах А и В на Земле, удаленных на расстояние l = 10
км, произошли одновременно два события. Найти время, разделяющее эти события, с точки зрения наблюдателя на космическом корабле, удаляющегося от Земли вдоль прямой АВ со скоростью v = 0,8 с
(с – скорость света в вакууме).
158. Релятивистская частица с массой m и кинетической энергией
Ек налетает на покоящуюся частицу с такой же массой. Найти массу
составной частицы, образовавшейся в результате соударения.
46
159. Релятивистская частица с массой m и кинетической энергией
Ек налетает на покоящуюся частицу с той же массой. Найти скорость
составной частицы, образовавшейся в результате соударения.
160. Найти скорость частицы, кинетическая энергия которой
Ек = 500 МэВ и импульс Р = 865 МэВ/с∗, где с – скорость света.
161. При какой скорости кинетическая энергия частицы равна ее
энергии покоя?
162. Найти скорость, при которой релятивисткий импульс частицы в n = 2 раза превышает ее ньютоновский импульс.
163. Сколько энергии (в расчете на единицу массы) надо затратить, чтобы сообщить первоначально покоившемуся космическому
кораблю скорость v = 0,980 с (с – скорость света в вакууме)?
164. Полная энергия мезона в n = 8 раз больше его энергии покоя. Найти скорость мезона.
165. Вычислить импульс протона с кинетической энергией
Ек = 500 МэВ.
166. На экваторе некоторой планеты тело весит в два раза меньше, чем на полюсе. Найти период обращения планеты вокруг собст3
венной оси. Плотность вещества планеты ρ = 3,0.10 кг/м3.
167. Телу сообщили на полюсе Земли скорость v0, направленную
вертикально вверх. Зная радиус Земли и ускорение свободного падения на ее поверхности, найти высоту, на которую поднимется тело.
168. Найти радиус круговой орбиты стационарного спутника
Земли, который остается неподвижным относительно ее поверхности.
Какова скорость спутника?
169. Найти период обращения спутника, движущегося вокруг некоторой планеты вблизи ее поверхности, если средняя плотность
планеты ρ = 3,3 г/см3.
Импульс релятивистской частицы обычно выражают в единицах: энергия/с, где с = 3.108
м/с – скорость света в вакууме. Например, если энергия выражается в МэВ (1МэВ = 1,6.10–13
Дж), то импульс выражается в МэВ/с. Использование такой единицы импульса упрощает
многие расчеты.
∗
47
КОНТРОЛЬНАЯ РАБОТА №2
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.
ЭЛЕКТРОСТАТИКА
ОСНОВНЫЕ ФОРМУЛЫ
Молекулярная физика
1. Количество вещества или число молей
ν=
N
m
= ,
NA
M
(1Ф)
где N – число молекул (атомов) вещества;
NA – постоянная Авогадро (находится из таблицы);
m – масса вещества (газа);
М – молярная масса вещества (находится из таблицы).
2. Уравнение Менделеева – Клапейрона (уравнение состояния
идеального газа)
(2Ф)
РV = νRT ,
где Р, V – давление и объем газа;
ν – число молей;
R – универсальная газовая постоянная (находятся из таблицы);
T – термодинамическая температура.
3. Зависимость давления газа от концентрации молекул n и температуры Т (уравнение состояния идеального газа)
Р = nkT,
(3Ф)
где k – постоянная Больцмана (находится из таблицы).
4. Основное уравнение молекулярно-кинетической теории газов
Р=
2
n εk ,
(4Ф)
3
где bεk d – средняя кинетическая энергия поступательного движения
молекулы
ε k = 3 kT .
2
48
(5Ф)
5. Средняя квадратичная скорость молекул массой m0
vкв =
3kT
3RT
=
.
m0
M
(6Ф)
Термодинамика
6. Молярные теплоемкости тела (газа) при постоянном объеме СV
и постоянном давлении СР:
i
i+2
CV = R ; CP =
R,
(7Ф)
2
2
где i – число степеней свободы молекулы.
7. Внутренняя энергия газа
i
U = ν RT = νCV T.
(8Ф)
2
8. Первое начало термодинамики
Q = ∆U + A ,
(9Ф)
где Q – количество теплоты, сообщенной газу;
∆U – приращение внутренней энергии;
A – работа, совершенная газом против внешних сил.
9. Работа при расширении газа от объема V1 до объема V2
A = ∫ РdV :
V2
(10Ф)
V1
а) при изобарном процессе
A = Р (V2 − V1 ) = νR∆T ;
б) при изотермическом процессе
А = νRT ln(V2/V1).
10. Работа газа при адиабатическом процессе
i
A = – ΔU = – ν CV ∆T , или A = ν ('1 – '2),
2
11. Уравнение Пуассона для адиабатического процесса
(11Ф)
(12Ф)
(13Ф)
PV γ = const, или 'g γ –1 = const, P' γ/(1– γ) = соnst,
(14Ф)
где γ = Cp /CV – постоянная адиабаты.
12. Коэффициент полезного действия (КПД) тепловой машины
η = (Q1 – Q2 )hQ1 ,
49
(15Ф)
где Q1 – тепло, полученное рабочим телом от нагревателя;
Q2 – тепло, переданное рабочим телом холодильнику.
13. КПД идеального цикла Карно (теорема Карно)
η = (T1 – T2 )hT1 ,
(16Ф)
где T1 и T2 – термодинамические температуры нагревателя и холодильника.
14. Приращение энтропии для замкнутых равновесных процессов
S2 − S1 = ∫
2
δQ ,
T
1
(17Ф)
где S1, S2 – энтропия в начальном и конечном равновесных состояниях системы;
δQ – элементарное количество теплоты;
Т – температура системы, при которой она получает тепло δQ.
Электростатика
15. Закон Кулона
F=
q1q2
,
2
4 πε 0 r
(18Ф)
где F – модуль силы взаимодействия двух точечных зарядов q1 и q2 ;
r – расстояние между зарядами;
ε0 – электрическая постоянная, находится из таблицы.
Закон Кулона записан для вакуума (воздуха).
16. Напряженность электрического поля, создаваемого системой n
точечных зарядов, равна векторной сумме напряженностей, создаваемых каждым зарядом (принцип суперпозиции электрических полей),
E = ∑ Ei ,
n
(19Ф)
i =1
где Ei – напряженность поля, создаваемого i-тымм зарядом.
17. Модуль напряженности электрического поля:
а) точечного заряда
q ,
E=
4πε 0 r 2
50
(20Ф)
где – расстояние от заряда j до точки, в которой определяется напряженность поля;
б) двух разноименно заряженных бесконечных параллельных
плоскостей
|ϭ1 | + |ϭ2 |
,
E=
(21Ф)
2ε0
где ϭ1, ϭ2 – поверхностные плотности зарядов.
При |ϭ1 | = |ϭ2 | = σ напряженность Е = σ/ε0. В таком виде
формула справедлива для плоского конденсатора, в котором расстояние между пластинами много меньше их линейных размеров;
в) равномерно заряженной бесконечно длинной нити (или цилиндра радиуса R) на расстоянии r от нити (или оси цилиндра)
τ
,
Е=
(22Ф)
2πε0 r
где τ = j ⁄dl – линейная плотность заряда. Для цилиндра r > R, так
как внутри цилиндра напряженность поля Е = 0.
18. Потенциальная энергия взаимодействия двух точечных зарядов
q q
W= 1 2 ,
(23Ф)
4π ε0 r
где q1, q2 – величины зарядов;
r – расстояние между зарядами.
Потенциальная энергия положительная при взаимодействии одноименных зарядов и отрицательная при взаимодействии разноименных
зарядов.
19. Потенциал электрического поля точечного заряда j на расстоянии r от заряда
q
.
φ=
(24Ф)
4π ε0 r
Такая же формула используется для нахождения потенциала заряженной металлической сферы радиусом R и зарядом q в точке на
расстоянии r > R от центра сферы. Потенциал поля внутри и на поверхности сферы φ = q/4πε0R.
51
20. Потенциал электрического поля, создаваемого системой n точечных зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности (принцип суперпозиции)
n
φ = φi ,
i=1
(25Ф)
где φi – потенциал поля заряда qi .
21. Связь между напряженностью поля и потенциалом φ:
а) для поля, обладающего центральной или осевой симметрией,
dφ
,
Er = –
(26Ф)
dr
где производная dφ/dr, берется вдоль линии напряженности Е;
б) для однородного поля
φ –φ
(27Ф)
E= 1 2 ,
d
где d – расстояние между эквипотенциальными поверхностями с потенциалами φ1 и φ2 вдоль линии напряженности .
22. Работа, совершаемая электрическим полем по перемещению заряда q из точки 1 в точку 2,
(28Ф)
А = q(φ1 – φ2),
где (φ1 – φ2) – разность потенциалов между начальной 1 и конечной 2
точками перемещения.
23. Электроемкость уединенного проводника
q
C= ,
(29Ф)
φ
где q – заряд, сообщенный проводнику;
φ – потенциал проводника.
24. Электроемкость конденсатора
q
q
,
=
(30Ф)
С=
φ1 – φ2
U
где φ1 – φ2 = U – разность потенциалов или напряжение между обкладками конденсатора;
q – модуль заряда одной обкладки конденсатора.
25. Электроемкость проводящего шара (сферы)
C = 4πεεa R ,
(31Ф)
где R – радиус шара;
52
ε – диэлектрическая проницаемость среды;
ε0 – электрическая постоянная (находится из таблицы).
26. Электроемкость плоского конденсатора
ε ε0 S
,
C=
( 32Ф)
d
где S – площадь одной пластины;
d – расстояние между пластинами.
27. Электроемкость системы из n конденсаторов, соединенных
последовательно,
1 .
1
=
Ci
C
n
i=1
(33Ф)
28. Электроемкость системы из n конденсаторов, соединенных
параллельно,
C = Ci .
n
(34Ф)
i=1
29. Энергия заряженного конденсатора
q! CU2 qU
.
W=
=
=
(35Ф)
2C
2
2
Энергию заряженного конденсатора удобно вычислять через ту
из величин q или U, которая в данном процессе остается постоянной.
Если заряд конденсатора не изменяется (конденсатор отключен от источника напряжения), то W = q2 /2C; если напряжение не изменяется
(конденсатор подключен к источнику напряжения), то W = (CU2 )/2
независимо от того, как меняется электроемкость конденсатора.
Примеры решения задач
Пример 1. В двух теплоизолированных сосудах объемами
V1 = 3,00 л и V2 = 5,00 л находится одинаковый идеальный газ при
давлениях P1 = 400 кПа, P2 = 600 кПа и температурах T1 = 300 К,
T2 = 400 К. Сосуды соединяют трубкой. Какая температура установится в сосудах после смешивания газов?
53
V1 = 3,00.10 м3,
–3
V2 = 5,00.10 м3,
–3
Р1 = 400 кПа,
Р2 = 600 кПа,
Т1 = 300 К,
Т2 = 400 К.
Т=?
Решение
Внутренняя энергия газов, находящихся в
первом и втором сосудах до их смешивания,
равна (см. (8Ф)):
U1 =
i
i
ν1 RT1 , U2 = ν2 RT2 ,
2
2
(1)
где i – число степеней свободы молекул газа;
ν1 , ν2 – число молей газов в первом и втором
сосудах;
R = 8,31 Дж/(моль.К) – универсальная газовая постоянная (находится из таблицы).
Используем уравнение Менделеева – Клапейрона (2Ф) для газов
в первом и втором сосудах:
P1 V1 = ν1 RT1 , P2 V2 = ν2 RT2 .
(2)
Сравнивая первые и вторые формулы в равенствах (1), (2), получим
i
i
U1 = P1 V1 , U2 = P2 V2 .
(3)
2
2
Общая энергия газов в сосудах до их соединения U ' = U1 + U2 ,
или, учитывая (3), получим:
i
U ' = P1 V1 + P2 V2 ).
(4)
2
После смешивания газов (соединение сосудов трубкой) установится искомая температура T и внутренняя энергия газа (8Ф)
i
U " = νRT, или, учитывая ν = ν1 + ν2 , получим:
2
i
U " = RT ( ν1 + ν2 ).
(5)
2
Число молей ν1 и ν2 найдем из уравнений (2) и подставим в (5). В
результате получим
! g!
i 0 g0
U"= +
) T.
6)
2 T1
T2
Сосуды теплоизолированные, поэтому U ' = U "(закон сохранения
энергии), откуда с учетом (4) и (6) найдем искомую температуру:
P1 V1 + P2 V2 )T1 T2
= 365 К.
T=
P1 V1 T1 + P2 V2 T2
54
Пример 2. Кислород массой m = 6,4 г находится при температуре T1 = 300 К и расширяется при постоянном давлении, при этом
объем увеличивается в n = V2/V1 = 2,0 раза. Найти количество теплоты, сообщенной газу.
Решение
–3
Используем первое начало термодинамики (9Ф)
m = 6,4.10 кг,
Т1 = 300 К,
Q = ∆U + A.
(1)
V2/V1 = n = 2,0.
Количество теплоты, сообщенной газу, идет
Q=?
на приращение внутренней энергии ∆U газа и на
совершение газом работы A против внешних сил. Приращение внутренней энергии ∆U = U2 – U1, или, учитывая (8Ф), получим
i m
(2)
∆U = . R∆T,
2 M
где i = 5 – число степеней свободы молекул двухатомного кислорода;
R = 8,31 Дж/(моль.К) – универсальная газовая постоянная (находится из таблицы);
M = 32 ∙ 10–3 кг/моль – молярная масса кислорода (находится из
таблицы);
∆T – приращение температуры. Работа газа при изобарном процессе (11Ф)
m
A=
R∆T .
(3)
M
С учетом (2) и (3), количество теплоты (1) запишется следующим
образом:
m
i
(4)
Q=
R ∆T + 1 ,
M
2
где ∆Т = Т2 – Т1.
Применяя уравнение Менделеева – Клапейрона (2Ф) для изобарного процесса, получим V1 ⁄T1 = V2 ⁄T2 , откуда, с учетом условия задачи, конечная температура после изобарного расширения
V2
T = nT1 .
T2 =
V1 1
55
Тогда приращение температуры
∆T = T2 – T1 = T1 ( n – 1).
Подставляя это выражение в (4), получим
i
m
RT1 ( n – 1)( + 1).
Q =
M
2
Учитывая условие задачи и табличные данные, найдем искомое
количество теплоты:
7 m
Q =
RT = 1,7 кДж.
2M 1
Пример 3. Объем одного моля ( ν = 1) идеального газа с числом
степеней свободы молекул i изменяется по закону V = а/Т, где a –
постоянная величина. Найти количество теплоты, полученной газом в
этом процессе, если его температура испытала приращение ∆T.
ν = 1,
i,
V = a/T,
∆T.
Q=?
Решение
Количество теплоты находится из первого начала
термодинамики (9Ф)
Q = ∆U + A.
(1)
Приращение внутренней энергии одного моля газа
∆U = U2 – U1, или, учитывая (8Ф), получим
i
∆U = R∆T ,
(2)
2
где R = 8,31 Дж/(моль.К) – универсальная газовая постоянная (берется из таблицы). Работа газа (10Ф)
A = H PdV.
(3)
Воспользуемся уравнением Менделеева – Клапейрона (2Ф) для
одного моля газа (ν = 1)
PV = RT,
откуда, учитывая условие задачи,
2
RT RT
P=
=
.
V
a
56
(4)
Продифференцируем условие задачи V = а/Т
a
dV = – 2 dT.
T
Подставляя (4) и (5) в формулу (3), найдем работу:
A = – R∆T .
С учетом (2) и (6) количество теплоты (1) равно
i
Q = R∆T ( − 1).
2
(5)
(6)
Пример 4. Два моля идеального газа находятся при температуре
T1 = 300 К и охлаждаются изохорно, в результате давление газа
уменьшилось в n = P1/P2 = 2,0 раза. Затем газ изобарно расширяется
так, что в конечном состоянии его температура стала равной первоначальной. Найти количество теплоты, сообщенной газу в данном
процессе.
Решение
T1 = 300 K,
P1/P2 = n = 2,0,
ν = 2.
Q=?
Р
Р1
1
Р2
2
P1,V1,T1
3
P2,V1,T2
0
V1
P2,V2,T1
V2
V
Рис. 20
Решение задачи упрощается, если заданные процессы изобразить
на ,g-диаграмме (см. рис. 20). Количество теплоты находится из
первого начала термодинамики (9Ф)
Q = ∆U + A.
(1)
В данной задаче на участке 1 – 2 (изохора) объем не изменяется
(рис. 20) и работа A12 = 0 (см. (10Ф), где dV = 0). Следовательно, работа совершается газом только на участке 2 – 3 при изобарном расширении А23 = А = P2(V2 – V1). Используем формулу работы газа для
57
изобарного процесса (см. (11Ф)), где для нашей задачи ∆Т = Т1 – Т2
(см. рис. 20). В результате получим
A = νR(T1 – T2).
(2)
Применяя уравнение Менделеева – Клапейрона (2Ф) к состояниям газа 1 и 2 при изохорном процессе (см. рис. 20), получим:
P0 P!
=
,
T0 T!
откуда, учитывая условие задачи,
T2 =
P2
T0
T 1= .
P1
n
Подставим эту формулу в уравнение (2) и найдем работу, совершенную газом в данном процессе:
1
A = νRT1 (1 − n ).
(3)
Приращение внутренней энергии (см. (8Ф))
i
∆U = νRΔT,
2
где i – число степеней свободы.
В данном сложном процессе начальная и конечная температуры
равны (на рис. т. т. 1 и 3), следовательно, ∆U = 0. Тогда из (1) искомое количество теплоты Q = A. Учитывая формулу (3), получим:
1
Q = νRT1 1 − = 2,5 кДж.
n
Пример 5. Водород H2 массой m = 20,0 г находится при температуре T1 = 300 К. Его объем при адиабатическом процессе увеличился
в n = V2/V1 = 5,00 раз, затем при изотермическом процессе уменьшился до прежнего значения. Найти: температуру T2 в конце адиабатического расширения; работу газа и приращение внутренней энергии при этих процессах.
58
Решение
Н2,
m = 20,0.10–3 кг,
Т1 = 300 К,
V2/V1 = n =5,00.
T2 = ? A1, A2 = ?
∆U1, ∆U2 = ?
Процессы расширения и сжатия газа изобразим графически в системе координат P,V (см.
рис. 21). Параметры газа можно определить из
уравнений адиабатического и изотермического
процессов. При адиабатическом процессе температура и объем газа в состояниях 1 и 2 связаны
между собой уравнением Пуассона (14Ф)
T1 V1 γ – 1 = T2 V2 γ – 1 ,
откуда, учитывая условие задачи, получим:
'0
,
(1)
nγ – 1
где постоянная адиабаты γ = CP / CV . Для молекулярного водорода
(число степеней свободы i = 5) молярная теплоемкость при постоянi + 2R = 7 R,
ном давлении (7Ф) C p =
P
2
2
1
адиабата
где R = 8,31 Дж/(моль.К) – универсальная газовая постоянная (находится из
изотерма
3
таблицы). Молярная теплоемкость при
2
5
i
постоянном объеме CV = R = R , то2
2
гда γ = 1,4. Подставляя это значение γ в
0
V1
V2
V
(1), найдем температуру: T2 = 158 К.
Рис. 21
Работа газа при адиабатическом расширении (см. (13Ф), где число молей ν = m/M)
m i
A1 =
R (T1 − T2 ) = 29,5 кДж.
(2)
M 2
T2 =
Учтем, что молярная масса водорода M = 2·10–3 кг/моль (находится из таблицы). Работа газа при изотермическом процессе (12Ф)
для нашей задачи (см. рис. 21)
V1
m
A2 =
RT2 ln .
M
V2
59
Учитывая условие задачи и выражение (1), найдем работу при
изотермическом сжатии:
mRT1 1
A2 =
ln = – 21,1 кДж.
(3)
Mnγ – 1 n
Знак «минус» показывает, что при сжатии газа работа совершается внешними силами. Для определения приращения внутренней энергии газа при адиабатическом процессе воспользуемся первым началом термодинамики (9Ф)
Q = ∆U + A.
В данном процессе Q = 0, и приращение внутренней энергии при
адиабатическом расширении с учетом (2) равно
∆U1 = – A1 = – 29,5 кДж.
При изотермическом процессе Т = const и ∆Т = 0. Следовательно,
im
R∆Т = 0.
∆U2 =
2M
Пример 6. У тепловой машины, работающей по циклу Карно,
температура нагревателя T1 в n = 1,6 раза больше температуры холодильника T2 . За один цикл машина производит полезную работу
А = 12 кДж. Какая работа A' за цикл затрачивается внешними силами
на изотермическое сжатие рабочего тела?
Решение
Воспользуемся теоремой Карно: коэффициент
Т1/Т2 = n = 1,6,
полезного действия (КПД) η тепловой машины, раA = 12 кДж.
ботающей по циклу Карно, зависит только от температур нагревателя T1 и холодильника T2 и не завиA' = ?
сит от природы рабочего тела и устройства тепловой
машины (см. (16Ф))
T2
.
η=1–
(1)
T1
Учитывая условие задачи, получим коэффициент полезного действия машины:
n–1
(2)
η= n .
60
КПД цикла Карно запишем через работу A и тепло Q1 , переданное рабочему телу от нагревателя: η = A⁄Q1 , откуда с учетом (2)
nA .
Q1 =
(3)
n–1
Работа A находится через Q1 и тепло Q2 , переданное от рабочего
тела холодильнику,
A = Q1 – Q2 ,
Откуда, учитывая (3), получим
A .
Q2 =
(4)
n–1
Применим к изотермическому сжатию первое начало термодинамики (9Ф) в следующем виде:
Q = ∆U – A' ,
(5)
где Q – тепло, переданное рабочему телу. В нашей задаче Q = – Q2,
так как тепло отнимается от тела и передается холодильнику;
∆U – приращение внутренней энергии рабочего тела. У нас
∆U = 0, так как Т = const (см. (8Ф));
A' – искомая работа внешних сил над рабочим телом. В результате из (5) имеем A' = Q2 . Используя (4), найдем
A
= 20 кДж.
A' =
n–1
Пример 7. Водород совершает цикл Карно. Найти КПД цикла,
если при адиабатическом расширении: а) объем газа увеличивается в
n = V2/V1 = 2,0 раза; б) давление уменьшается в n = Р1/Р2 = 2,0 раза.
а)
V2
= n = 2,0
V1
;
P
б) 1 = n = 2,0.
P2
η1 = ? η2 = ?
Решение
а) Воспользуемся формулой КПД цикла Карно (16Ф)
η=1–
T2
,
T1
(1)
где T1 , T2 – температура нагревателя и холодильника.
61
Используем для адиабатического процесса уравнение Пуассона
(14Ф) в виде
откуда имеем
T1 V1 γ – 1 = T2 V2 γ – 1 ,
T2
V1 γ – 1
,
=W X
T1
V2
(2)
где γ = 1,4 – постоянная адиабаты для двухатомного водорода. По
условию задачи V1 ⁄V2 = 1⁄n. Тогда из (2)
γ–1
T2
1
= WnX
= n 1– γ .
T1
Подставляя это выражение в (1), найдем КПД цикла Карно при
увеличении объема газа в n = 2,0 раза
η1 = 1 – n1 – γ = 0,24.
б) Запишем уравнение Пуассона в следующем виде (см. (14Ф)):
P1 T1
откуда
γ
1uγ
Т2
Т1
= P2 T2
=
Р1
γ
1uγ
1_ γ
γ
Р2
,
,
или, учитывая условие задачи, получим
1
Т2
=n γ .
Т1
_γ
С учетом этого выражения, из (1) найдем КПД цикла, когда давление уменьшается в n = 2,0 раза
η 2 =1 − n
1− γ
γ
= 0,18.
Пример 8. Один моль гелия при изобарном расширении увеличил свой объем в n = V2/V1 = 4,0 раза. Найти приращение энтропии.
62
ν = 1 моль,
V2/V1 = n = 4,0,
P = const.
∆S = ?
Решение
Приращение энтропии находится из второго начала термодинамики для равновесных процессов
(17Ф)
2
δQ ,
∆S = ∫
(1)
T
1
где δQ – элементарное количество теплоты, находится из первого начала термодинамики (9Ф), записанного в дифференциальной форме,
δQ = dU + δA.
(2)
Приращение внутренней энергии для одного моля газа (см. (8Ф))
dU =
i
R dT,
(3)
2
где R = 8,31 Дж/моль∙К) – универсальная газовая постоянная (находится из таблицы). Элементарная работа газа
δA = P dV.
(4)
Продифференцируем уравнение состояния идеального газа (2Ф)
для одного моля (ν = 1) с учетом того, что процесс изобарный:
P dV = R dT.
Тогда (4) запишется следующим образом:
δA = R dT.
Подставляя (3) и (5) в уравнение (2), получим:
i
δQ = R W + 1X dT.
2
Подставим это выражение в (1) и проинтегрируем:
(5)
2
i
dT
i
T2
,
∆S = R W + 1X H = R W + 1X ln
T1
2
T
2
1
(6)
где i = 3 – число степеней свободы атомов гелия.
Применяя уравнение Менделеева – Клапейрона (2Ф) к состояниям газа при изобарном процессе, получим с учетом условия задачи:
V2
T2
=
=n.
T1
V1
63
Используя это соотношение, из (6) найдем приращение энтропии:
i
∆S = R( + 1) ln n = 29 Дж/К .
2
Пример 9. Один моль двухатомного идеального газа находится
при температуре T1 = 300 К и сжимается от объема V1 до объема
V2 = V1/2 один раз изотермически, а другой – адиабатически. Найти
приращение энтропии и конечную температуру T2 в обоих процессах.
Решение
Для нахождения приращения энтропии испольν = 1 моль,
зуем второе начало термодинамики (17Ф)
T1 = 300 К,
δQ .
V2 = V1/2.
∆S = ∫
(1)
T
∆S1 = ? ∆S2 = ?
Элементарное количество теплоты δw находитT2 = ?
ся из первого начала термодинамики (9Ф)
δQ = dU + δA,
(2)
где dU – приращение внутренней энергии. При изотермическом процессе dU = 0 (см. (8Ф)). Элементарная работа газа
δА = PdV .
(3)
Из уравнения Менделеева–Клапейрона (2Ф), записанного для одного моля (ν = 1), найдем: P = RT/V, и подставим это выражение в
(3). В результате получим
dV .
δA = RT
(4)
V
Учитывая dU = 0, из (2) и (4) получим
dV .
δQ = RT
V
Подставляя это выражение в (1), найдем приращение энтропии
при изотермическом сжатии:
V
∆S1 = R ∫ dV = R ln 2 .
V1
V1 V
V2
64
Учитывая условие задачи V2 = V1/2 и табличное значение универсальной газовой постоянной R = 8,31 Дж/(моль.К), получим искомое
приращение энтропии:
∆S1 = – R ln2 = – 5,76 Дж/К.
Знак «минус» означает, что энтропия при этом процессе уменьшается, так как макросистема не является замкнутой.
Для адиабатического процесса δQ = 0, тогда из (1) видно, что
∆S2 = 0, т. е. энтропия при данном процессе остается постоянной.
Температура при изотермическом процессе не изменяется, следовательно, по условию задачи конечная температура в этом процессе
Т2 =T1 = 300 К. Для адиабатического процесса используем уравнение
Пуассона (14Ф) в виде: T1 V1 γ – 1 = T2 V2 γ – 1 , откуда
T2
V1 γ – 1
.
=W X
(5)
T1
V2
Постоянная адиабаты γ = C P / С V . Используя формулы молярных
теплоемкостей C P и С V (7Ф), найдем γ = (i + 2)/i. В задаче дан двухатомный газ, для которого число степеней свободы i = 5, тогда γ =
1,4. Учитывая условие задачи V2 = V1/2, получим из (5)
T2 = 2 γ – 1 T1 = 396 К .
Таким образом, конечная температура больше при адиабатическом сжатии.
Пример 10. Точечные закрепленные заряды q1 = 40 нКл и
q2 = – 10 нКл находятся на расстоянии r = 10 cм друг от друга. Где
следует поместить третий заряд q3, чтобы он находился в равновесии?
При каком знаке заряда q3 равновесие будет устойчивым?
q1 = 40 нКл,
q2 = – 10 нКл,
r = 10 cм.
х=?
Решение
Равновесие заряда j1 возможно, если векторная сумма сил, действующих на него, равна нулю. Следовательно, для нашего случая на заряд
j1 действуют две силы, равные по модулю и противоположные по направлению – F1 = – F2 , или
(1)
F1 = F2.
65
Учитывая величины и знаки зарядов q1 и q2, легко понять, что условие (1) выполняется в точке C, находящейся на прямой, проходящей через эти заряды и расположенной справа от заряда q2 (см.
рис. 22, где заряд q3 > 0).
q1
q2
x+r
F2
x
q3
q1
F1
С
Рис. 22
q2
F1
x+r
x
q3 F2
С
Рис. 23
Используя закон Кулона (18Ф) и обозначения на рис. 22, запишем
модули сил взаимодействия заряда q3 с зарядами q1 и q2 (см. рис. 22):
F1 =
q1q3
4πε 0 ( x + r )
2
, F2 =
q2 q3
.
4πε0 x 2
(2)
С учетом этих формул, уравнение (1) примет вид:
q1
xq2 x
.
=
2
2
(x + r)
x
Откуда, учитывая условие задачи, получим: х = r = 10 см. Нашли
положение точки (т. С на рис. 22), в которой заряд q3 находится в
равновесии. Если при смещении заряда от положения равновесия
возникают силы, возвращающие его в прежнее положение, то равновесие называется устойчивым. Найдем знак заряда q3, при котором
равновесие будет устойчивым.
Возьмем отношение сил Кулона (2)
q! x + r 2
F2
r 2
=y y W
X ~ {1 + | .
F1
q1
x
x
(3)
При смещении заряда j1 > 0 из положения равновесия (точка C
на рис. 22) вправо, расстояние x увеличивается, а отношение F2 ⁄F1
уменьшается (см. (3)). Следовательно, ! уменьшается быстрее, чем
66
0 , и равнодействующая сил 0 , ! направлена вправо от положения
равновесия, т. е. заряд j1 под действием этой силы будет удаляться от
точки С. При смещении заряда j1 влево величина x уменьшается
(рис. 22), а отношение ! ⁄0 увеличивается (см. (3)). Следовательно,
! возрастает быстрее, чем 0 . Это означает, что равнодействующая
этих сих направлена влево от положения равновесия и заряд j1 будет
смещаться также влево. Таким образом, когда j3 > 0 при его смещении от положения равновесия, заряд не возвращается в прежнее положение. Следовательно, равновесие заряда будет неустойчивым.
Если заряд q3 < 0, то сила притяжения 0 со стороны заряда q1 бу-
дет направлена влево, а сила отталкивания ! со стороны заряда q2
направлена вправо (см. рис. 23). При смещении заряда q3 вправо (x
увеличивается) из (3) видно, что F2/F1 уменьшается, т. е. сила !
уменьшается быстрее, чем 0 (F2 < F1), и их равнодействующая направлена влево от точки равновесия C. Под действием этой силы q3
будет смещаться также влево, т. е. возвращаться к положению равновесия (т. С). При смещении q3 влево (x уменьшается) отношение F2/F1
увеличивается (см. (3)) и F2 > F1. Равнодействующая этих сил направлена вправо и заряд q3 будет возвращаться к положению равновесия (точка С на рис. 23). Следовательно, при q3 < 0 равновесие заряда будет устойчивым. Величина заряда j1 на его равновесие не
влияет (см. (3)).
Если заряды q1 и q2 не закреплены, и заряд q3 и вся система зарядов
находится под действием только кулоновских сил, то такая система
всегда находится в неустойчивом равновесии (теорема Ирншоу).
Пример 11. Тонкий прямой стержень длиной 2C заряжен равномерно зарядом j. Найти модуль напряженности электрического поля
и потенциал поля в точке на прямой, совпадающей с осью стержня и
находящейся на расстоянии r > C от его центра.
67
Решение
2C,
j,
r > C.
=? φ=?
~
0
−C
2C
j
C
X
Рис. 24
Выделим на заряженном стержне малый элемент dx (см. рис. 24).
Заряд dq из-за малости этого элемента можно считать точечным. Модуль напряженности поля точечного заряда dq равен (см. (20Ф))
=
|j |
.
!
4πεa
(1)
Заряд j выразим через линейную плотность τ заряда стержня
j = τ , где τ = j ⁄2C. С учетом этого, выражение (1) запишется
следующим образом:
=
|j |
8πεa C
!
.
(2)
Из условия задачи ясно, что напряженности от всех элементов
стержня направлены в одну сторону и при j > 0 направлены против
оси X (см. рис. 24). Поэтому для нахождения модуля напряженности
поля от всего стержня нужно выражение (2) проинтегрировать по
всей его длине от r – a до r + a (см. рис.), т. е. воспользоваться принципом суперпозиции
r}a
|j |
H !.
=
8πεa C
rua
Осуществляя интегрирование в указанных пределах, получим искомый модуль напряженности:
=
|j |
.
2
2
4πεa (r − a )
68
Отсюда при r ≫ a следует
|j |
.
4a r 2
Получили напряженность поля точечного заряда, т. е. заряженный стержень при r ≫ a можно считать точечным зарядом.
Для нахождения потенциала поля заряженного стержня запишем
потенциал поля точечного заряда j = (j ⁄2C) (см. (24Ф), где
φ = dφ, q = dq, r = x)
qdx
.
dφ =
(3)
8πε0 ax
Воспользуемся, как и при нахождении модуля напряженности ,
принципом суперпозиции, т. е. проинтегрируем (3) по всей длине
=
стержня от r – a до r + a (см. рис. 24). В результате получим искомый
потенциал
j
r+a
.
φ=
ln
8πε0 a r – a
Пример 12. Заряд q > 0 равномерно распределен по тонкому
кольцу радиусом R. Найти напряженность электрического поля Е на
оси кольца в точке, находящейся на расстоянии а от его центра.
Решение
Выделим на кольце малый элемент *. От этого элемента
напряженность составляет угол α с осью X (см. рис. 25).
Из соображений симметрии следует, что сумма (интегральная) проекций от всех элементов dl кольца равна нулю
j > 0,
,
C.
=?
( y = 0). Следовательно, результирующая напряженность E направ-
лена по оси кольца и совпадает с осью Х (см. рис. 25). Модуль этой напряженности равен интегральной сумме проекций P от всех элементов кольца ( = P ). Так как заряд j элемента * кольца можно
считать точечным, то напряженность поля этого заряда (см. (20Ф))
j
,
(1)
E =
4π εa r2
69
где r – расстояние от элемента * до точки С, в которой находится
напряженность .
*
0
r
C
α
С
Y
P
~
Рис. 25
~
X
Проекция вектора на ось X равна P = cosα (см. рис. 25).
Учитывая (1), где заряд j выражается через линейную плотность τ
(j = τ*), получим
P
=
τ*
cosα.
4π εa r!
(2)
=
τ cosα
.
!
2 εa r
(3)
Проинтегрируем это выражение, учитывая, что величины τ и α
являются постоянными для всех элементов кольца, и интегралы
P = , * = 2π. В результате получим
Из рис. 25 имеем
r = C ! + ! ,
cos α =
√C !
C
+
!
.
Подставляя эти выражения в (3) и учитывая плотность заряда
τ = j ⁄2π , найдем модуль напряженности:
=
jC
.
⁄
!
!
3
!
(
)
4π εa C + Из этой формулы видно, что при а >> R модуль напряженности
= j ⁄4π εa C2 , т. е. на больших расстояниях от заряженного кольца
70
величина Е находится так же, как от точечного заряда (см. (20Ф)).
Напряженность поля Е направлена вдоль оси Х (см. рис. 25).
Пример 13. Бесконечно длинный цилиндр радиусом R = 15 см
заряжен с поверхностной плотностью σ = 15 мкКл⁄м2 . Найти работу
при перемещении заряда q = 4,0 мкКл из точки 1 в точку 2, находящиеся от оси цилиндра, соответственно, на расстоянии r1 = 30 см и
r2 = 15 см (см. рис. 26).
Решение
R = 0,15 м,
Z
σ = 15·10–6 Кл⁄м2 ,
q = 4,0∙10–6 Кл,
r1 = 0,30 м,
r2 = 0,15 м.
А=?
r2
2
r1
1
Y
X
Рис. 26
Работа электрического поля по перемещению заряда q (cм. (28Ф))
#э = j(φ1 − φ2 ).
(1)
Для нахождения разности потенциалов воспользуемся формулой
(22Ф), где модуль линейной плотности (заряд единицы длины цилиндра) τ = τ, т. к. в нашей задаче поверхностная плотность ϭ > 0
Е=
τ .
2πε 0 r
(2)
Заряд, находящийся на поверхности цилиндра высотой h, равен
τh. Этот же заряд, записанный через поверхностную плотность ϭ равен 2πRhϭ. Откуда получается связь между τ и ϭ: τ = 2πRϭ. В результате формула (2) запишется следующим образом:
σ
=ε .
0r
71
(3)
Далее, воспользуемся формулой (26Ф)
dφ
=− .
dr
Из (3) и (4) имеем
(4)
σ dr .
dφ = − ε
0r
Интегрирование этого уравнения в пределах от r1 до r2 дает приращение потенциала
r2
σR r
σR dr
φ2 – φ1 = – ε H r = – ε ln r2 .
0
0
1
r1
Откуда разность потенциалов между начальной 1 и конечной 2
точками перемещения (см. рис. 26) составит
σ r
φ1 − φ2 = ε ln r2 .
0
1
Подставляя это выражение в (1), получим работу по перемещению заряда j из точки 1 в точку 2
σj r
Aэ = ε ln r2 = – 0,16 Дж.
a
1
Работа электрического поля отрицательная, поскольку положительный заряд перемещается из точки 1 с меньшим потенциалом в
точку 2 с большим потенциалом (см. рис. 26). Искомая работа (работа
внешних сил) А = – Аэ = 0, 16 Дж.
Пример 14. В схеме, изображенной на рис. 27, электрические емкости конденсаторов C1 = 1,00 мкФ, C2 = 2,00 мкФ, C1 = 3,00 мкФ и
напряжение между клеммами A и B равно U = 100 В. Найти общую
электроемкость системы, заряд и напряжение на каждом конденсаторе.
72
C0 = 1,00 мкФ,
C! = 2,00 мкФ,
C1 = 3,00 мкФ,
U = 100 В.
C = ? q0 , q! = ?
U1, U2, U3 = ?
Решение
А
С2
С1
U
В
С3
С2
Рис. 27
Система конденсаторов состоит из двух параллельных ветвей,
напряжения на которых одинаковы и равны U (см. рис. 27). Одна
ветвь состоит из конденсатора емкостью C1 , другая – из трех последовательно соединенных конденсаторов емкостью C2 и C3 . Емкость
системы последовательно соединенных конденсаторов С ′ находится
из формулы (см. (33Ф))
1
C'
откуда
=
CY =
2
1
,
+
C! C1
C! C1
.
C! + 2C1
(1)
При параллельном соединении конденсаторов емкость системы
(34Ф) C = C0 + C Y . Учитывая (1), получим:
C=
C1 C2 + C3 (2C1 + C2 )
= 1,75 мкФ.
C2 + 2C3
Для нахождения зарядов конденсаторов используем формулу
электроемкости конденсатора (30Ф)
C=
q
.
U
(2)
Напряжение на конденсаторе емкостью C1 равно U (см. рис. 27).
Следовательно, заряд этого конденсатора (см. (2))
q1 = C1 U = 100 мкКл.
73
В результате электростатической индукции заряды последовательно соединенных конденсаторов емкостью C2 , C3 и C2 будут равны между собой и заряду j Y системы или батареи этих конденсаторов: q2 = q3 = j Y . Напряжение на батарее равно U, следовательно, заряд j Y можно найти из формулы (2), в которой C = C Y . Используя (1),
найдем заряд трех последовательно соединенных конденсаторов
j2 = j3 =
C2 C3 U
= 75 мкКл.
C2 + 2C3
Напряжение на конденсаторе емкостью C1 равно U1 = U =100 В.
Напряжение на конденсаторах емкостью C2 , C3 находится из формулы
(2). Используя найденные заряды на этих конденсаторах, получим:
q3
q2
= 37,5 В, U3 =
= 25 В.
(3)
U2 =
C2
C3
Очевидно, сумма напряжений на трех последовательно соединенных конденсаторах равна U = 100 В. Из полученных результатов
(3) видно: 2U2 + U3 = 100 В, что соответствует условию задачи.
ТАБЛИЦА ВАРИАНТОВ К КОНТРОЛЬНОЙ РАБОТЕ № 2
Таблица содержит варианты для специальностей, учебными планами которых предусмотрено четыре контрольных работы.
Вариант
0
1
2
3
4
5
6
7
8
9
1
201
202
203
204
205
206
207
208
209
210
2
211
212
213
214
215
216
217
218
219
220
Номера задач
3
4
221
231
222
232
223
233
224
234
225
235
226
236
227
237
228
238
229
239
230
240
74
5
241
242
243
244
245
246
247
248
249
250
6
251
252
253
254
255
256
257
258
259
260
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
201. Найти концентрацию молекул водорода при давлении
Р = 300 Па, если средняя квадратичная скорость его молекул
vкв = 2,5.103 м/с.
202. Средняя квадратичная скорость молекул газа при нормальных
условиях vкв = 460 м/с. Найти число молекул в газе массой m = 1,00 г.
203. Водород массой m = 0,30 г находится в сосуде объемом
V = 2,0 л при давлении Р = 200 кПа. Найти среднюю квадратичную
скорость и среднюю кинетическую энергию молекул водорода.
204. В баллоне объемом V = 0,01 м3 находится газ при температуре t = 27 °С. Из-за утечки газа давление уменьшилось на 4,1 кПа.
Сколько молекул вышло из баллона при постоянной температуре?
205. В баллоне объемом V = 0,20 м3 находится газ под давлением
Р1 = 100 кПа и при температуре Т1 = 290 К. После накачивания газа
давление Р2 = 300 кПа и температура Т2 = 320 К. На сколько увеличилось число молекул газа в баллоне?
206. Найти внутреннюю энергию U воздуха в комнате объемом
V = 40 м3 при нормальном атмосферном давлении. Зависит ли величина U от температуры воздуха в комнате при постоянном давлении?
207. Баллон, содержащий азот массой m1 = 1,0 кг, при испытании
взорвался при температуре t1 = 350 °C. Какую массу водорода m2
мож-но хранить в этом баллоне при температуре t2 = 20 °C, имея пятикратный запас прочности?
208. По газопроводу течет углекислый газ при давлении
Р = 500 кПа и температуре t = 17 °C. Найти скорость движения газа в
трубе, если за время τ = 5,0 мин через поперечное сечение трубы
площадью S = 6,0 см2 протекает газ массой m = 2,5 кг?
209. Спутник объемом V = 10 м3 погрузился в тень Земли. При
этом температура внутри спутника, вначале равная t = 27 °С, понизи-
лась на k = 1,0 % и давление воздуха уменьшилось на ∆Р = – 1,05
кПа. Найти массу воздуха в спутнике.
75
210. Два одинаковых по объему баллона, содержащих газ при
одинаковой температуре Т = 273 К, соединены трубкой диаметром
d = 5,0 мм (рис. 28). Посередине трубки находится капелька ртути,
которая делит весь сосуд на два равных объема
d
V
V
V = 200 см3. На какое расстояние сместится капелька, если один баллон нагреть на ∆Т = 2,0 К,
Рис. 28
а другой на столько же охладить?
211. Два теплоизолированных баллона наполнены воздухом и соединены короткой трубкой с краном. Объемы баллонов, а также давление и температура воздуха в них равны V1, Р1, Т1 и V2, Р2, Т2. Найти
давление воздуха, которое установится после открытия крана.
212. Два баллона наполнены одинаковым газом при одной и той
же температуре. Масса и давление газа в сосудах соответственно равны: m1 = 0,20 кг, m2 = 0,30 кг и Р1 = 400 кПа, Р2 = 900 кПа. Баллоны
соединяются трубкой, объемом которой можно пренебречь. Найти
установившееся давление газа в баллонах, если температура увеличилась на k = 20 % от первоначальной.
213. Цилиндрический сосуд, расположенный горизонтально, заполнен газом при температуре Т1 = 300 К и давлении Р1 = 0,10 МПа.
Сосуд разделен на две равные части подвижной (нет трения) теплоизолированной перегородкой. Каким станет давление газа в сосуде,
если в одной его половине газ нагреть до температуры Т2 = 330 К, а в
другой половине температуру оставить без изменения?
214. Для приготовления ванны емкостью V = 200 л смешали холодную воду при температуре t1 = 10 °С с горячей водой при темпе-
ратуре t2 = 60 °С. Какие объемы той и другой воды надо взять, чтобы
температура смеси была θ = 40 °С? Нагревание ванны не учитывать.
215. До какой температуры необходимо нагреть алюминиевый
кубик, чтобы при помещении его на лед он погрузился в него до
уровня верхней грани? Температура льда θ = 0 °С.
216. Свинцовая пуля, летящая со скоростью v1 = 400 м/с, проби-
вает доску и вылетает из нее со скоростью v2 = 100 м/с. Какая часть
76
пули при этом расплавится, если на увеличение ее внутренней энергии идет k = 60 % кинетической энергии? Температура пули в момент
удара t = 50 °С.
217. Железный метеорит массой m = 80 кг при температуре
t = 39 °С влетает со скоростью v = 1400 м/с в атмосферу Земли. Счи-
тая, что на нагревание и плавление метеорита идет k = 80 % его кинетической энергии, определить, какая масса метеорита расплавится.
218. Определить, расплавится ли полностью железный метеорит,
падающий на поверхность Луны со скоростью v = 2,0 км/с, если его
температура до столкновения с Луной t = 30 °С. На увеличение внут-
ренней энергии метеорита идет k = 40 % его кинетической энергии.
219. Два свинцовых шара с одинаковой массой движутся навстречу друг другу со скоростями v и 2v. Насколько увеличится тем-
пература шаров в результате их неупругого удара при v = 2,0 м/с?
220. Какое количество теплоты необходимо сообщить водороду
массой m = 10 г, находящемуся при температуре t1 = 27 °C, чтобы
при постоянном давлении его объем увеличился в n = 2 раза?
221. Азот массой m = 15 г находится в закрытом сосуде при температуре Т1 = 300 К. Какое количество тепла необходимо сообщить
азоту, чтобы средняя квадратичная скорость его молекул возросла в
n = 2,0 раза?
222. Водород, находящийся при нормальных условиях в закрытом
сосуде объемом V = 5,0 л, охлаждается на ∆Т = – 55 К. Найти приращение внутренней энергии газа и количество отданного им тепла.
223. Кислород массой m = 10 г находится под давлением
о
Р = 300 кПа и температуре t1 = 10 С. После изобарного нагревания
газ занял объем V2 = 10 л. Найти: изменение внутренней энергии; работу, совершенную газом при расширении; количество теплоты, полученное газом.
224. Два моля идеального газа при постоянном давлении нагрели
на ∆Т = 72 К, сообщив ему количество теплоты Q = 4,8 кДж. Найти
77
совершенную газом работу, приращение его внутренней энергии и
число степеней свободы молекул газа.
225. В вертикальном цилиндрическом сосуде под поршнем массой m = 10 кг и площадью сечения S = 20 см2 находится одноатомный газ. Первоначально поршень находился на высоте h = 20 см от
дна сосуда, а после нагревания газа поршень поднялся на высоту H =
25 см. Найти количество теплоты, сообщенное газу в процессе нагревания. Атмосферное давление Р0 = 100 кПа. Трением и теплообменом газа с сосудом и поршнем пренебречь.
226. Воздух находится при 0 °С. До какой температуры охладится
воздух при адиабатическом увеличении его объема в два раза?
227. В горизонтальном теплоизолированном цилиндрическом
сосуде под поршнем находится ν = 0,50 моля гелия. Поршень массой
m = 1,0 кг сначала удерживается, а затем отпускается. Какую скорость приобретет поршень к моменту, когда температура гелия
уменьшится на ∆Т = – 10 К? Атмосферным давлением, а также трением и теплообменом газа с сосудом и поршнем пренебречь.
228. Водород массой m = 20 г находится при нормальных условиях и сжимается от объема V1 до объема V2 = V1/2. Найти работу газа при изотермическом и адиабатическом процессах.
229. Воздух сжимается от объема V1 до объема V2 = V1/2 сначала
адиабатически, а затем изотермически. В каком процессе совершается меньшая работа и во сколько раз?
230. Кислород массой m = 10 г находится при нормальных условиях. Найти давление и температуру газа при изотермическом и
адиабатическом сжатии до объема V2 = 1,4 л.
231. На диаграмме (см. рис. 29) представлена зависимость давления
одноатомного газа от объема. Найти количество теплоты, полученное
или отданное газом при переходе из состояния 1 в состояние 3.
232. Одноатомный газ сначала охладили (1 – 2), уменьшив давление в n = 2 раза, а затем нагрели (2 – 3) до первоначальной температуры T1 = 360 К (см. рис. 30). Количество вещества ν = 2 моля. Найти
количество теплоты, полученное газом на участке 2 – 3.
78
Р, кПа
30
2
V
3
3
20
1
10
0
1
2
2
0
3
3 V, м
1
360
Т, K
Рис. 30
Рис. 29
233. Тепловой двигатель, работающий по циклу Карно, имеет
температуру нагревателя t1 = 227 °С и холодильника t2 = 127 °С. Во
сколько раз надо увеличить температуру нагревателя, чтобы КПД
двигателя увеличился в n = 3 раза?
234. КПД η реального теплового двигателя составляет k = 50 %
от КПД ηид идеального двигателя, работающего по циклу Карно в том
же интервале температур. Температура нагревателя t1 = 227 °С, температура холодильника t2 = 77 °С. Найти мощность двигателя, если
за время τ = 1,0 ч потребляется уголь массой m = 200 кг с удельной
теплотой сгорания q = 30 МДж/кг.
235. Найти приращение энтропии при изохорном и изобарном нагревании аргона массой m = 8,0 г, если его абсолютная температура в
обоих процессах увеличилась в n = 2 раза.
236. Воздух массой m = 1,0 кг, сжимаясь адиабатически, уменьшил свой объем в n1 = 6 раз, а затем при постоянном объеме его давление увеличилось в n2 = 1,5 раза. Найти приращение энтропии в
этом процессе.
237. Гелий массой m = 1,7 г, адиабатически расширяясь, увеличил
свой объем в n = 3,0 раза и затем изобарно сжимается до первоначального объема. Найти приращение энтропии газа в этом процессе.
238. Во сколько раз необходимо увеличить при постоянной температуре объем газа в количестве ν = 4,0 моля, чтобы его энтропия
увеличилась на ∆S = 23 Дж/К?
239. Кислород массой m = 1,0 кг, находящийся при давлении
Р1 = 0,50 МПа и температуре Т1 = 400 К, изобарно расширяясь, уве-
79
личил объем в n = 2 раза, а затем сжимается изотермически до давления Р2 = 4,0 МПа. Найти суммарное приращение энтропии.
240. Два моля газа изохорно охлаждаются, а затем изобарно расширяются до первоначальной температуры. Найти приращение энтропии, если давление газа в данном процессе изменилось в n = 3,3 раза.
241. С какой силой будут взаимодействовать два медных шарика
массой m = 1,0 г каждый, если у η = 1 % атомов одного шарика взять
по одному электрону и перенести их на другой шарик? Расстояние
между центрами шариков r = 1,0 м.
242. Два заряда q1 = 1,1 нКл и q2 = 4,4 нКл находятся на расстоянии r = 12 см друг от друга. Где нужно поместить третий заряд q3,
чтобы система зарядов находилась в равновесии? Будет ли это равновесие устойчивым? Найти величину заряда q3.
243. В вершинах квадрата помещены одинаковые заряды
q = 1,0 мкКл каждый. Какой заряд нужно поместить в центр квадрата, чтобы данная система зарядов находилась в равновесии?
244. Два одинаковых шарика плотностью ρ1 подвешены на нитях
равной длины, закрепленных в одной точке. Шарикам сообщаются
одинаковые заряды, после чего они погружаются в жидкость плотностью ρ2. Определить диэлектрическую проницаемость жидкости, если
угол расхождения нитей в воздухе равен α, а в жидкости – β.
245. Вокруг положительного заряда q вращаются по круговой орбите, располагаясь в углах квадрата со стороной а, четыре одинаковые частицы массой m каждая, имеющие одинаковые отрицательные
заряды – q. В центре этого квадрата находится положительный заряд
q. Определить частоту вращения частиц по орбите.
246. В вершинах правильного шестиугольника со стороной а помещены друг за другом заряды + q, + q, + q, – q, – q, – q. Найти напряженность электрического поля в центре шестиугольника.
247. Одинаковые заряды величиной q = 1,0 нКл каждый расположены в трех вершинах квадрата со стороной а = 40 см. Найти напряженность поля в четвертой вершине квадрата.
248. Тонкий стержень длиной а = 10 см заряжен равномерно зарядом q = 0,20 мкКл. Найти напряженность электрического поля в
80
точке, лежащей на оси стержня на расстоянии r = 30 см от его ближайшего конца.
249. Тонкое кольцо радиусом R = 25 см имеет заряд q = 5,0
мкКл, равномерно распределенный по кольцу. Найти работу электрических сил при перемещении точечного заряда q0 = 10 мкКл из центра кольца по произвольному пути в точку, находящуюся на оси
кольца на расстоянии l = 50 см от его центра.
250. Найти потенциал капли ртути, получившейся от слияния n
«малых» капель, каждая из которых была заряжена до потенциала ϕ0.
251. Два одинаково заряженных металлических шара имеют потенциалы ϕ1 = 20 В и ϕ2 = 30 В. Каким будет потенциал шаров, если
их соединить проволокой? Расстояние между шарами велико по
сравнению с их радиусами.
252. Два электрона находятся на бесконечно большом расстоянии
и двигаются навстречу друг другу с одинаковыми по модулю скоростями v = 1,0·106 м/с. Найти наименьшее расстояние, на которое они
сблизятся.
253. Два электрона находятся на бесконечно большом расстоянии
друг от друга. В начальный момент времени один из электронов покоился, а второй двигался по направлению к первому со скоростью v.
Найти наименьшее расстояние, на которое они сблизятся.
254. Протон и α-частица, двигаясь с одинаковой скоростью, влетают в плоский конденсатор параллельно его пластинам. Какая частица больше отклонится электрическим полем конденсатора от своей
первоначальной траектории и во сколько раз?
255. Расстояние между пластинами плоского вакуумного конденсатора d = 16 мм, длина пластин l = 3,0 см. В конденсатор параллельно его пластинам влетает электрон со скоростью v = 2,0⋅106 м/с.
На какое расстояние сместится электрон в направлении, перпендикулярном пластинам, к моменту вылета его из конденсатора, если напряжение между пластинами U = 4,8 В.
256. Три конденсатора емкостью С1 = 10 мкФ, С2 = 20 мкФ,
С3 = 30 мкФ соединены в батарею (см. рис. 31). Напряжение между
точками А и В равно U = 20 В. Найти заряд на каждом конденсаторе.
81
257. В электрической цепи (см. рис. 32) емкости конденсаторов
С1 = 1,0 мкФ, С2 = 2,0 мкФ, С3 = 3,0 мкФ. Напряжение между точками А и В равно U = 12 В. Найти заряд на каждом конденсаторе.
258. В электрической цепи (рис. 32) емкости конденсаторов
С2 = С3 = С, С1 = 2С. Напряжение между точками А и В U = 500 В.
Энергия батареи конденсаторов W = 5,0 Дж. Найти емкости конденсаторов.
С2
С1
В
А
С2
А
С3
С1
В
С3
Рис. 31
Рис. 32
259. Однородное электрическое поле напряженностью
Е = 10 кВ/м образовано двумя заряженными параллельными пластинами (плоский воздушный конденсатор), расстояние между которыми
d = 2,0 см. Между пластинами параллельно им помещается металлический лист толщиной d1 = 0,50 см. Найти напряжение между пластинами после внесения металлического листа.
260. Плоский конденсатор с диэлектриком из парафина подключен
к источнику постоянного напряжения. Расстояние между пластинами d1
= 4,2 см. Как нужно изменить расстояние между пластинами, чтобы
при удалении диэлектрика энергия конденсатора осталась неизменной?
Изменится ли результат, если конденсатор будет отключен от источника тока? Диэлектрическая проницаемость парафина ε = 2,1.
261. Одинаковые по величине и по знаку точечные заряды помещены в вершинах правильного треугольника и шестиугольника. Какой заряд q противоположного знака надо поместить в центре этих
систем, чтобы они находились в равновесии?
262. Какую минимальную работу против сил электрического поля надо совершить, чтобы собрать каплю ртути радиусом R с зарядом
q из n одинаковых заряженных капель?
82
ПРИЛОЖЕНИЯ
1. Основные физические константы
Нормальное ускорение свободного падения
Средний радиус Земли
Скорость света в вакууме
Гравитационная постоянная
Нормальные условия
Постоянная Авогадро
Постоянная Больцмана
Универсальная газовая постоянная
Электрическая постоянная
Масса электрона
Модуль заряда электрона
g = 9,81 м/с2
Rз = 6,37.106 м
с = 3.108 м/с
G = 6,67.10–11 м3/(кг.с2)
Р0 = 105 Па, Т0 = 273 К
NA = 6,02 1023 моль–1
k = 1,38.10 –23 Дж/К
R = 8,31 Дж/(моль.К)
ε0 = 8,85.10–12Ф/м
me = 9,1.10–31 кг
е = 1,6.10–19 Кл
2. Молярная масса М, 10–3 (кг/моль)
Н2
2
Не
4
О2
32
N2
28
СО2
44
Сu
64
3. Удельная теплоемкость с, 103 Дж/(кг.К)
Алюминий ………….0,90
Железо ………………0,46
Свинец ………………………...0,13
Вода…………………………......4,18
4. Удельная теплота плавления λ, 103 Дж/кг
Железо ………………270
Лед……………………330
Свинец ………………25
83
СОДЕРЖАНИЕ
Предисловие............................................................................................................................3
Программа курса физики для инженерно-технических специальностей
заочного отделения вуза ........................................................................................................4
Часть Ι. Механика.
Молекулярная физика и термодинамика .........................................................................4
Электростатика...................................................................................................................5
Библиографический список ..............................................................................................5
Методические указания к решению задач и выполнению
контрольных работ.............................................................................................................6
Контрольная работа № 1. Механика ................................................................................8
Таблица вариантов к контрольной работе № 1 .............................................................38
Задачи для самостоятельного решения..........................................................................38
Контрольная работа №2. Молекулярная физика и термодинамика. Электростатика...48
Основные формулы .........................................................................................................48
Таблица вариантов к контрольной работе № 2 .............................................................74
Задачи для самостоятельного решения..........................................................................75
Приложения ..........................................................................................................................83
Учебное издание
ГОЛОВАНОВА Татьяна Николаевна;
ШТЕРЕНБЕРГ Александр Моисеевич
Сборник задач по физике и примеры их решения
Часть I
Редактор В.В. Прокопова
Компьютерная верстка И.О. Миняева
Выпускающий редактор Н.В. Беганова
Подписано в печать 09.06.16.
Формат 60×84 1/16. Бумага офсетная
Усл. п. л. 4,88. Уч.-изд. л. 4,85.
Тираж 150 экз. Рег. № 80/16
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Самарский государственный технический университет»
443100, г. Самара, ул. Молодогвардейская, 244. Главный корпус
Отпечатано в типографии
Самарского государственного технического университета
443100, г. Самара, ул. Молодогвардейская, 244. Корпус № 8
84