ДИФРАКЦИЯ СВЕТА:
advertisement

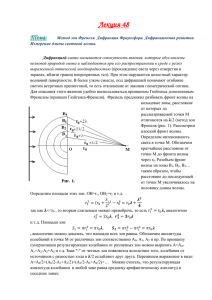
ДИФРАКЦИЯ СВЕТА: Принцип Гюйгенса-Френеля Зоны Френеля Дифракция Френеля от круглого отверстия Дифракция Френеля от круглого диска Использованы материалы из Internet С НОВЫМ ГОДОМ! Дифракцией называется совокупность явлений, проявляющихся в перераспределении светового потока в результате суперпозиции волн, наблюдаемых при распространении света в среде с резкими неоднородностями (при условии, что обе неоднородности ). Дифракция приводит к проникновению света в область геометрической тени. Принцип Гюйгенса, согласно которому любая точка пространства, до которой дошло волновое возмущение, становится источником вторичных волн, причем огибающая эти вторичные волны представляет собой поверхность волнового фронта, позволяя решать лишь задачи о направлении распространения светового фронта и не затрагивая по существу вопроса об интенсивности волн, идущих по равным направлениям. Принцип Гюйгенса – Френеля можно сформулировать следующим образом: каждый элемент волновой поверхности S служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS. В точку P от каждого участка dS, приходит a0dS колебание dE K cost kr 0 , где K r зависит от угла между нормалью n к площадке dS и направлением от dS к точке P. Результирующее колебание в точке P представляет собой суперпозицию колебаний, взятых для всей волновой поверхности S: a0 E k cost kr dS - аналитическое r S выражение принципа Гюйгенса – Френеля. Рассмотрим действие световой волны, испущенной из точки S в какой-либо точке наблюдения P. Согласно принципу Гюйгенса – Френеля заменим действие источника S действием воображаемых источников, расположенных на волновой поверхности. Разбиваем поверхность на кольцевые зоны, симметричные относительно прямой SP таким образом, чтобы расстояния от краев зоны до P отличалось на ½λ. • При таком разбиении площади всех зон Френеля оказываются одинаковыми. Докажем это. Выберем произвольно m - зону. bm 2 a rm x O A ax B b 2 2 rm a a x b m b x 2 2 a 2 a 2 2ax x 2 b2 mb m 2 b2 2bx x 2 2 2 2 2ax 2bx mb m b xm 2a b 4 Площади m 1) -сегмента соответственно равны: ab S m 2 xm m ab ab S m 1 m 1 ab m - сегмента и ( Площадь зоны Френеля определится как разности площадей сегментов Sm Sm Sm1 ab ab Хотя площади зон Френеля равны, зоны видны из точки наблюдения под разными углами, поэтому амплитуды колебаний, возбуждаемых волнами, идущими от различных зон будут различны. Пусть действие первой зоны (центральной) возбуждает в точке B колебание с амплитудой A1, второй A2 и т.д., причем A1>A2>A3>… Благодаря выбранному способу разбиения действия соседних зон ослабляют друг друга, т.к. разность хода волны от соседних зон λ/2, то они приходят в точку B в противофазе и накладываясь ослабляют друг друга. Таким образом, Aрез = A1 – A2 + A3 – A4 + … = = A1 – (A2 – A3) – (A4 – A5) – … т.к. A2>A3, A4>A5, то A2 – A3 > 0 и A4 – A5 > 0 … и Aрез<A1 Iрез< I1 Амплитуда результирующего колебания в точке B, получающегося вследствие взаимной интерференции света, идущего в точку B от различных участков нашей сферической волны, меньше амплитуды, создаваемой действием одной лишь первой зоны. Таким образом, действие всей волны на точку B сводится к действию её малого участка, меньшего, чем центральная зона, площадь ab 4 которой . Для 5 10 мм , a и b=1м, площадь ab действующей части волны меньше 1мм 2. Следовательно, распространение света от A к B действительно происходит так, как если бы световой поток шел внутри очень узкого канала вдоль AB, т.е. прямолинейно. Если результирующую амплитуду несколько преобразовать, то A1 A1 A3 A3 A5 Aрез A2 A4 ..., 2 2 2 2 2 Am 1 Am 1 учтя Am в силу монотонного 2 A1 убывания, получим . Aрез 2 Таким образом, если оставить открытой только первую зону Френеля, то интенсивность света в точке P будет в 4 раза больше, чем при отсутствии преграды (т.к. A1 2 Aрез ). Оценим радиус произвольной зоны Френеля 2 m b rm a a 2 a b 2 2 2 m ab m b 2 2 a a a b 4 a b 2 2 2 Учитывая малость 2 ab ab rm m rm m. ab ab 2 Хорошей иллюстрацией, подтверждающей метод зон Френеля, может служить опыт с зонной пластинкой, которая изготавливается следующим способом. Изготавливают экран, состоящий из последовательно чередующихся прозрачных и непрозрачных колец, радиусы которых удовлетворяют соотношению для rm при заданных a, b и λ. Приготовленный таким образом экранчик носит название зонной пластинки. Волновой фронт, профильтрованный через такую зонную пластинку в тоже наблюдение дает: Aрез A1 A3 A5 ... , если открыта центральная зона, т.е. Aрез значительно большую, чем при полностью открытой волновой поверхности. Пластина играет роль линзы с фокусным r 2m расстоянием f m mab Действительно rm ab a b m 2 ab rm 2 1 1 1 . Сравним с формулой для линзы 2 a b rm m 1 1 1 . a b С помощью зонной пластинки можно достичь еще большей яркости изображения, если не задерживать колебания, приходящие в точку B от четных зон, а сообщить им изменения фазы на π. Такая пластинка называется фазовой зонной пластинкой. Дифракция Френеля от круглого отверстия Пусть сферическая волна, идущая из точки A, встречает на своем пути экран с круглым отверстием. Исследуем явление в точке B, лежащей на линии, соединяющей A с центром круглого отверстия. В зависимости от размера отверстия в нем уложится больше или меньше число зон, что и определит результат дифракции в точке B. Если расстояния a и b удовлетворяют mab соотношению r0 , то число зон, ab укладывающихся в отверстие радиусом r0 будет 2 r0 1 1 m , а амплитуда в точке наблюдения a b будет равна A A1 A2 A3 ... Am Если опять воспользоваться представлением A3 A3 A5 A1 A1 A A2 A4 ... 2 2 2 2 2 A1 Am то A , если m 2k 1, т.е. нечетное и 2 2 A1 Am 1 A Am , если m 2k , т.е. четное 2 A Am 1 2 A1 Am m , поэтому Am A 2 2 2 2 Если отверстие открывает одну или небольшое нечетное число зон, то действие в точке B будет больше, чем в отсутствие экрана. Если же отверстие открывает четное число зон, то световое возбуждение в точке B будет меньше, чем при свободной волне. Наименьшая освещенность соответствует двум открытым зонам. По мере перемещения точки наблюдения вдоль прямой AB число открытых зон будет меняться и в точке наблюдения максимум будет сменяться на минимум интенсивности и так далее. Если перемещаться в направлении, перпендикулярном направлению АВ, то в отверстие будут укладываться зоны частично. Результат будет зависеть от того действие каких зон перевесит. Дифракция Френеля от диска Поместим между источником света A и точкой наблюдения B непрозрачный круглый диск радиуса r0 . Диск закроет m первых зон Френеля, амплитуда в точке B будет A Am 1 Am 2 Am 3 ... Am 1 Am 1 Am 3 Am 2 ... 2 2 2 Am 1 2 Характер картины на экране можно выяснить с помощью тех же самых рассуждений, что и выше. В случае непрозрачного круглого диска дифракционная картина имеет вид чередующихся светлых и темных концентрических колец. В центре картины помещается светлое пятно. Если диск закрывает большое число зон Френеля, то светлое пятно в центре отсутствует, и освещенность в области геометрической тени практически всюду равна нулю. Если же отверстие открывает большое число зон Френеля, то внутри области, ограниченной геометрической тенью, освещенность оказывается практически постоянной. Чередование темных и светлых колец в обоих случаях наблюдаются лишь в очень узкой области на границе геометрической тени.