Лекция №2
advertisement

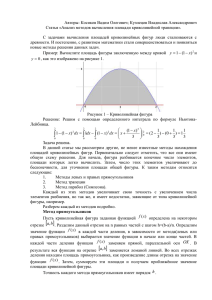
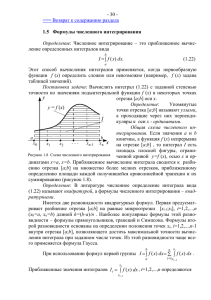
Лекция №2 Формулы для приближенного вычисления определенных интервалов применяется часто для большого числа элементарных функций, когда их первообразные нельзя выразить через элементарные функции, или когда функция подынтегральная задана таблично. Рассмотрим способы численного интегрирования. Формула прямоугольников I. Пусть требуется b f x dx . вычислить a Разобьем отрезок интегрирования на n равных частей. Каждый частичный отрезок обозначим n и назовем шагом деления Вычислим приближенно x . интеграл как площадь ступенчатой фигуры, взяв за основание прямоугольников «n», а за высоту левую ординату каждого частичного отрезка ; или . Обозначим ; ; ;… Следовательно: (1) – формула левых прямоугольников. Если за высоты прямоугольников принять ординаты правых прямоугольников, то получим аналогично: 7 (2) формула правых прямоугольников. Если считать, что n достаточно велико, что интегральная сумма должна мало отличаться от величины интеграла. II. Формула трапеций Величину интеграла найдём как сумму трапеций с высотами «∆x» и основаниями y0, y1, y2,…,yn. (3) формула трапеций Значение интеграла по формуле трапеций при том же разбиении, что и прямоугольников, более точный результат. III. Формула Симпсона (формула парабол) Наиболее точной формулой является формула Симпсона (формула парабол), так как для достижения той же точности вычисления можно брать меньше число точек деления отрезка интегрирования. 8 Формулу Симпсона называют ещё формулой параболических трапеций, поскольку геометрическая сущность её использования состоит в замене площади криволинейной трапеции, ограниченной кривой площадей параболических трапеций, построенных на суммой каждой паре вертикальных прямых (ординат). Формула Симпсона имеет вид: (4) Отрезок интегрирования в формуле Симпсона всегда имеет четное количество точек деления: 2n, тогда . Абсолютная погрешность формулы Симпсона ; где . Однако практическая ценность этой формулы невелика из-за сложности оценки М, поэтому на практике обычно используют прием двойного пересчета. Данный интеграл вычисляют по формуле Симпсона дважды: сначала при выбранном числе 2n, затем при удвоенном числе 4n. Сравнивая результаты I2n и I4n, полученные при первом и втором расчете, считают верными их совпадающие знаки. При этом погрешность: (5). Таким образом, если то полагают , где Е – допустимая погрешность, . Если же , то делают следующий пересчет при вновь удвоенном числе 8n и сравнивают I4n и I8n. Так поступают до тех пор, пока не достигнут нужной точности. В качестве начального обычно выбирают число 2n=4 частей деления отрезка интегрирования. В промежуточных действиях следует брать на один знак больше, чем требуемая точность вычисления интеграла. 9 Пример №1 Ширина реки равна 20 метров. Промеры глубины в некотором поперечном сечении 2 метра дали следующую таблицу: 9 № 0 1 2 3 4 x 0 2 4 6 8 0 0 0 1 1 y 0,2 0,5 0,9 0,1 0,3 5 6 7 8 1 1 1 1 0 2 1 0,7 4 2 0,1 1 0,5 0 1 8 6 2 0 0 1 0,1 1 0,6 0 0,2 Расстояние от одного из берегов X м., а соответственно глубина Y м. Найти площадь поперечного сечения реки. По формуле трапеций имеем: По формуле Симпсона: Пример №2 Вычислить интеграл по таблице, затем по формулам прямоугольников, трапеций и Симпсона. Сравнить результаты № x 0 1.0 1.00000 1 1.1 0.90909 2 1.2 0.83333 3 1.3 0.76923 10 4 1.4 0.74291 5 1.5 0.66667 6 1.6 0.62500 7 1.7 0.58824 8 1.8 0.55556 9 1.9 0.52632 10 2.0 0.50000 1) По формуле прямоугольников 2) По формуле трапеций 3) По формуле Симпсона Итак, при деление на n=10частей имеем: По формуле Симпсона 5 верных знаков; По формуле трапеций 3 верных знаков; По формуле прямоугольников 1 верный знак. 11 Графическое интегрирование IV. Графическое интегрирование – обладает, вообще говоря, малой точностью. Этот прием полезен, когда требуется иметь общее представление о графике первообразной или когда подынтегральная функция задана графически, а ее аналитическое выражение неизвестно. Пусть функция на отрезке x X a=x0 1 x … xn=b y … yn задана таблично 2 y Y y0 1 2 Построить график первообразной для этой функции – значит построить кривую , ордината в каждой точке X которой численно равна площади криволинейной трапеции с основанием ограниченной кривой . Технически построение 1) и осуществляется следующим образом: По заданным значениям исходной таблицы строим график функции по выбранному масштабу; 2) На каждом частичном отрезке выбираем точку (вообще-то говоря произвольную, мы будем брать середину отрезка) и строим ординаты этих точек , 3) ,… Получим точки М1, М2, …, Мn. Из точек М1, М2, …, Мn проведем прямые параллельные оси OX, получим М1, М2, …, Мn на оси OY. 4) На оси OX слева от точки О выберем точку Р(-1;0). 5) Из точки N0 проведем прямую N0N1 ║P до пересечения с ординатой точки X1 Из точки N1 проведем прямую N1N2 ║P и так далее. Получим график функции F(x) – ломанную. Соединив точки N0, N1, N2,… плавной линией получим интегральную кривую. 12 Замечание Точки Xi не обязательно брать равноотстоящими. Для увеличения точности построения рекомендуется в состав точек Xi включать точки графика (нули, точки экстремума, точки перегиба). 13