ГЛАВА: Введение в численные методы. Лекция №3: Численное

ГЛАВА: Введение в численные методы.
Лекция №3: Численное интегрирование (15 слайдов)
Слайд №1: Методы численного интегрирования.
Требуется вычислить определенный интеграл:
Методы решения такой задачи:
J=
Z b
a
y(x)dx.
1. Аппроксимация рядом Тейлора.
2. Построение квадратурных формул:
(a) Формулы Ньютона – Котеса.
(b) Метод Чебышева.
(c) Метод Лежандра – Гаусса.
3. Метод Монте-Карло.
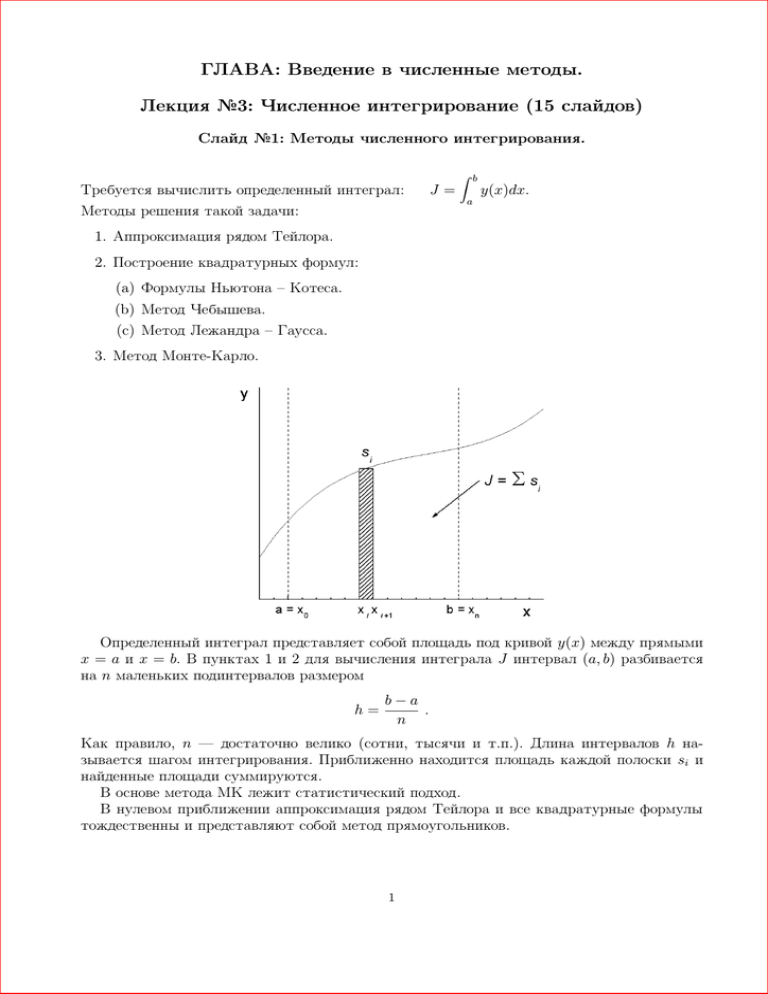
Определенный интеграл представляет собой площадь под кривой y(x) между прямыми
x = a и x = b. В пунктах 1 и 2 для вычисления интеграла J интервал (a, b) разбивается
на n маленьких подинтервалов размером
h=
b−a
.
n
Как правило, n — достаточно велико (сотни, тысячи и т.п.). Длина интервалов h называется шагом интегрирования. Приближенно находится площадь каждой полоски si и
найденные площади суммируются.
В основе метода МК лежит статистический подход.
В нулевом приближении аппроксимация рядом Тейлора и все квадратурные формулы
тождественны и представляют собой метод прямоугольников.
1
Слайд №2: Метод прямоугольников.
Суть метода.
Интервал интегрирования (a, b) разбивается на n равных отрезков длиной
b−a
.
n
h=
В качестве приближенного значения площади каждой полоски принимается площадь прямоугольника, ширина которого равна h, а высота — значению функции y(x) на левом краю
интервала. Локальная формула метода левых прямоугольников:
s i ' yi h ,
где yi = y(xi ) .
Общая формула метода левых прямоугольников:
J=
n−1
X
i=0
yi h = (y0 + y1 + . . . + yn−1 ) h .
Аналогично строятся формулы правых и центральных прямоугольников:
si ' yi+1 h ,
si ' yi+1/2 h ,
J=
n−1
X
i=0
J=
n
X
i=1
yi h = (y1 + y2 + . . . + yn ) h ;
³
´
yi+1/2 h = y0.5 + y1.5 + . . . + yn−1/2 h ,
где
yi+1/2 = y(xi + h/2) .
Приведенные формулы представляют собой частные примеры квадратурных формул ∗ .
Погрешность метода левых прямоугольников
Локальная погрешность:
ei ' h · (yi+1 − yi ) ' h · (yi + yi0 h − yi ) ∼ h2 .
Общую погрешность получим, суммируя погрешности на каждом шаге,
E ∼ n · ei ∼
b−a 2
h ∼h.
h
Таков же порядок погрешности (E ∼ h) и в методе правых прямоугольников, а вот в
методе центральных прямоугольников E ∼ h2 .
Недостатки метода:
• Высокая погрешность; для достижения высокой точности расчета приходится сильно
”мельчить” шаг интегрирования, что приводит к сильному увеличению временных
затрат.
2
Слайд №3: Аппроксимация рядом Тейлора.
Суть метода.
Интервал интегрирования (a, b) разбивается на n равных отрезков длиной
h=
b−a
.
n
Если вы на i-ом шаге знаете и значение функции yi = y(xi ), и значение производной yi0 , то
площадь i-ой полоски
si '
Z xi+1 ³
xi
³
yi + yi0 (x − xi ) + O (x − xi )2
´´
dx = yi h +
³ ´
yi0 2
h + O h3 .
2
Поскольку мы пренебрегли в итоге членами ∼ h3 , то погрешность расчета в этом случае
будет
E ∼ h2 .
e i ∼ h3 ,
Это на порядок лучше метода левых (правых) прямоугольников. Дальнейшее увеличение
точности достигается подключением старших производных. Так, используя вторую производную yi00 , получим
y0
y 00
si = yi h + i h2 + i h3 + . . . .
2
6
Суммарная погрешность расчета при подключении второй производной
E ∼ h3 .
И т.д.
(k)
si = yi h +
yi0 2 yi00 3
yi
h + h + ... +
hk+1 + O(hk+2 ) .
2
6
(k + 1)!
Чем больше производных вы примете во внимание, тем большей точности вы сможете
достичь. Если вы сможете определить весь ряд Тейлора для площади si , вы получите
точное значение интеграла. Если же вы точно учли первые несколько слагаемых, то погрешность вашего расчета определяется первым из отброшенных (неучтенных) членов.
Сравнение с приведенным выражением для si позволяет установить погрешность любого
другого метода численного интегрирования.
Недостатки метода:
• Необходимость расчета производных интегрируемой функции.
3
Слайд №4: Построение формул Ньютона – Котеса.
Интервал интегрирования (a, b) разбивается на n равных отрезков длиной h = (b − a)/n.
Для приближенной оценки площади i-ой полоски si подинтегральная функция y(x) на интервале (xi , xi+1 ) аппроксимируется конечным полиномом степени m
y(x) ' Pm (x) = yi + a1 (x − xi ) + a2 (x − xi )2 + . . . + am (x − xi )m .
Для определения коэффициентов полинома ai интервал (xi , xi+1 ) дополнительно разбивается на m одинаковых подинтервалов: xi , xi +h/m, xi +2h/m, . . ., xi +h = xi+1 . Используя
значения функции y(x) в узлах xi + jh/m (j = 1, . . . , m), составляется система уравнений













h
y(xi + h/m) = yi + a1 m
+ a2
³ ´2
h
+ a3
m
³ ´2
a2 2h
m
³ ´3
y(xi + 2h/m) = yi + a1 2h
+
+ a3
m
... ... ...
y(xi+1 ) = yi + a1 h + a2 h2 + a3 h3 + . . .
h
m
³
2h
m
+ ... ,
´3
+ ... ,
которая позволяет определить все коэффициенты ai . Далее непосредственно интегрируя
полином Pm (x) нетрудно получить весовые коэффициенты квадратурной формулы ∗ для
площади i-ой полоски
si '
Z xi+1
xi
Pm (x)dx =
m
X
j=0
cj yj .
Погрешность можно определить, сопоставляя результат с точным тейлоровским разложением. Но если подинтегральная функция y(x) представляет собой полином степени m, то
квадратурная формула даст точное значение интеграла. Это позволяет сформулировать
следующее условие для определения весовых коэффициентов cj : весовые коэффициенты
квадратурной формулы определяются таким образом, что полученная в итоге формула
точно интегрирует любой полином степени m. Данная задача однозначно решается для
любых m.
Ограничение полиномом нулевой степени (m = 0) приводит к методу прямоугольников,
полином первой степени (m = 1) определяет метод трапеций, второй (m = 2) — метод
парабол Симпсона, третьей (m = 3) — метод, называемый ”правилом трех восьмых”.
4
Слайд №5: Формулы Ньютона – Котеса: метод трапеций.
Интервал интегрирования (a, b) разбивается на n равных отрезков длиной
h=
b−a
.
n
В качестве площади i-ой полоски si принимается площадь трапеции, определяемой значениями подинтегральной функции y(x) на краях интервала (xi , xi+1 ).
Локальная формула метода трапеций:
si '
yi + yi+1
h.
2
Суммирование площадей всех трапеций дает общую формулу
J'
h
(y0 + 2y1 + 2y2 + . . . + 2yn−1 + yn ) .
2
Эта формула является первой из формул Ньютона – Котеса.
Погрешность метода трапеций.
Аппроксимируем значение yi+1 в локальной формуле тейлоровским рядом в i-ой точке
yi+1 = yi + yi0 h +
yi00 2
h + ... .
2
Подставляя это, для площади si получаем
si = yi h +
yi0 2 yi00 3
h + h ,
2
4
что до членов ∼ h2 совпадает со строгим тейлоровским разложением. Следовательно, погрешность в методе трапеций
E ∼ h2 .
e i ∼ h3 ,
По точности расчета метод трапеций эквивалентен методу центральных прямоугольников.
Недостатки метода:
• Высокая погрешность; для достижения высокой точности расчета приходится сильно
”мельчить” шаг интегрирования, что приводит к сильному увеличению временных
затрат.
5
Слайд №6: Формулы Ньютона – Котеса: метод Симпсона.
Интервал интегрирования (a, b) разбивается на n равных отрезков длиной h = (b − a)/n.
Для приближенной оценки площади i-ой полоски si подинтегральная функция y(x) на интервале (xi , xi+1 ) аппроксимируется полиномом второй степени.
Локальная формула метода Симпсона:
si =
Z xi+1
xi
y(x)dx '
´
h³
yi + 4yi+1/2 + yi+1 .
6
Общая формула метода Симпсона
J=
´
h³
y0 + 4y0+1/2 + 2y1 + 4y1+1/2 + 2y2 + . . . + 4yn−1/2 + yn .
6
Формула Симпсона является второй из семейства формул Ньютона – Котеса.
Погрешность формулы Симпсона.
E ∼ h4 .
Характерные свойства формулы Симпсона (ее незначительное усложнение по сравнению с методом трапеций или прямоугольников и, в то же время, значительное повышение
точности расчета) делают формулу Симпсона самым распространенным методом численного интегрирования.
6
Слайд №7: Старшие формулы Ньютона – Котеса.
Интервал интегрирования (a, b) разбивается на n равных отрезков длиной h = (b − a)/n.
Для приближенной оценки площади i-ой полоски si подинтегральная функция y(x) на интервале (xi , xi+1 ) аппроксимируется полиномом степени m.
Ограничение полиномом третьей степени (m = 3) дает третью формулу Ньютона –
Котеса, называемую ”правилом трех восьмых”:
3
J = h(y0 + 3y1 + 3y2 + 2y3 + 3y4 + 3y5 + 2y6 + 3y7 + . . .
8
+ 3yn−4 + 2yn−3 + 3yn−2 + 3yn−1 + yn ) .
Погрешность расчета по этой формуле оказывается такой же, как и по формуле Симпсона
E3 ∼ h4 .
Полином четвертой степени дает четвертую формулу Ньютона – Котеса
J=
2
h(7y0 + 32y1 + 12y2 + 32y3 + 14y4 + 32y5 + 12y6 + . . .
45
+ 14yn−4 + 32yn−3 + 12yn−2 + 32yn−1 + 7yn ) .
Погрешность четвертой формулы
E4 ∼ h6 .
Все формулы Ньютона–Котеса являются квадратурными формулами∗
J=
N
X
i=0
ci y(xi ) ,
узлы xi которых расположены эквидистантно, а свободными параметрами, за счет которых
достигается точное интегрирование полинома m степени, являются весовые коэффициенты
ci .
В противоположность формулам Нюьютона – Котеса в методе Чебышева свободными параметрами являются узлы квадратурной формулы и общий весовой коэффициент,
а в методе Лежандра – Гаусса (метод наивысшей алгебраической точности) — и узлы, и
весовые коэффициенты.
7
Слайд №8: Метод Чебышева.
Для численной оценки интеграла:
Z b
J =
a
y(x)dx ,
интервал интегрирования (a, b)
разбивается на n равных отрезков длиной h = (b−a)/n. Для приближенной оценки площади
i-ой полоски si строится квадратурная формула∗ (от интервала (xi , xi+1 ) удобно перейти
к (−1, +1))
Z +1
si =
−1
y(x)dx '
m
X
j=1
cj y(xj ) .
в которой свободными параметрами являются координаты узлов xj и общий весовой множитель c1 = c2 = . . . = cm = c.
Требуется, чтобы квадратурная формула точно интегрировала любой полином степени m:
Z +1
−1
Qm (x)dx =
m
X
j=1
cj Q(xj ) , Qm (x) = q0 +q1 x+q2 x2 +. . .+qm xm ,
для любых q1 , . . . , qm .
Базис в пространстве полиномов степени m: x0 , x1 , x3 , . . ., xm .
Нетрудно доказать, что к квадратурная формула точно интегрирует любой полином степени m тогда и только тогда, когда она точно интегрирует любой элемент базиса. Это
дает для определения свободных параметров систему из m + 1 уравнения
Z +1
−1
Z +1
−1
Z +1
−1
m
X
0
x dx =
j=1
x1 dx =
m
X
j=1
xm dx =
m
X
j=1
cj ,
cj x1j ,
→
mc = 2 ,
→
т.е. c =
x 1 + x2 + . . . + xm = 0 ,
...........................
cj x m
j ,
→
2
,
m
m
m
xm
1 + x2 + . . . + xm =
1 1 + (−1)m
.
c m+1
Последние m уравнений определяют координаты узлов xj .
Для m = 2
:
1
x2 = −x1 = √ ,
3
c=1.
1
2
c= .
x3 = −x1 = √ , x2 = 0 ,
3
2
И т.д. Координаты узлов всегда располагаются симметрично относительно нуля.
Погрешность метода Чебышева.
m-точечный метод Чебышева точно интегрирует полином степени m+1, и, следовательно,
по точности является аналогом m-ой формулы Ньютона – Котеса (для четных m). Так,
2-х точечный метод Чебышева — аналог методу Симпсона.
Недостатки метода:
Для m = 3
:
• Вещественные решения существуют только для n < 8 и n = 9.
• При заметном усложнении по сравнению с формулами Ньютона–Котеса точность интегрирования не повысилась.
8
Слайд №9: Метод Лежандра – Гаусса.
Для численной оценки интеграла:
J =
Z b
a
y(x)dx ,
интервал интегрирования (a, b)
разбивается на n равных отрезков длиной h = (b−a)/n. Для приближенной оценки площади
i-ой полоски si строится квадратурная формула∗ (от интервала (xi , xi+1 ) удобно перейти
к (−1, +1))
si =
Z +1
−1
y(x)dx '
m
X
j=1
cj y(xj ) .
в которой свободными параметрами являются координаты xj и весовые множители cj .
Требуется, чтобы квадратурная формула точно интегрировала любой полином степени
2m − 1:
Z +1
−1
Q(2m−1) (x)dx =
m
X
j=1
Q(2m−1) (x) = q0 + q1 x + . . . + q(2m−1) x2m−1 .
cj Q(2m−1) (xj ) ,
Произвольный полином Q2m−1 (x) всегда может быть представлен в виде
Q2m−1 (x) = Q0m−1 (x)Pm (x) + Q00m−1 (x) ,
где Pm (x) — полином Лежандра∗ степени m. В качестве m узлов квадратурной формулы
используются m действительных корней полинома Лежандра Pm (x). Используя известные
свойства данных полиномов можно показать, что условие, определяющее квадратурную
формулу, сводится к соотношению
Z +1
−1
Q00m−1 (x)dx
=
m
X
j=1
cj Q00m−1 (xj ) ,
которое дает m уравнений (см. метод Чебышева) для определения m оставшихся неизвестных — весовых коэффициентов cj .
Относительно весовых коэффициентов при заданных числах xi это — система линейных
алгебраических уравнений, решение которой существует для любых m.
При m = 2 :
q
x1,2 = ±1/ (3) ,
c 1 = c2 = 1 .
В случае двух узлов методы Лежандра–Гаусса и Чебышева тождественны.
При m = 3 :
√
x1,3 = ± 0.6 ,
x2 = 0 ,
c1,3 =
5
,
9
c2 =
8
.
9
И т.д. Для m-точечного метода Гаусса:
ci =
2
(1 −
x2i ) [Pn0 (xi )]2
.
Достоинства метода:
• Точно проинтегрировать полином степени (2m − 1) — это максимум, чего можно
достичь, используя информацию о m узлах подинтегральной функции. Поэтому метод
Лежандра – Гаусса называют методом наивысшей алгебраической точности.
9
Слайд №10: Метод Монте-Карло.
Требуется вычислить интеграл:
J=
Z b
a
y(x)dx .
Пусть на интервале (a, b) задана последовательность случайных чисел {xi } с законом распределения вероятностей f (x). Если подвергнуть эту последовательность функциональной
обработке
yi = y(xi ) ,
то математическое ожидание величины y дается соотношениями
Z b
My =
a
y(x)f (x)dx
Z b
n
1X
yi .
=
n i=1
f (x)dx
a
Чтобы получить исходный интеграл, достаточно рассмотреть математическое ожидание
величины y/f
Z b
My/f = Z ab
a
y(x)dx
f (x)dx
=
n
1X
yi
.
n i=1 f (xi )
В простейшем случае используется равномерный закон распределения f (x) = const, и
функция распределения нормируется на единицу
Z b
a
Это дает
J=
Z b
a
f (x) = 1 .
y(x)dx =
n
b−aX
y(xi ) .
n i=1
Погрешность определяется объемом выборки {xi } и согласно статистическому анализу
1
E∼√ .
n
Достоинства метода:
• Возможность остановить вычисления при любом значении n.
Оказывается предпочтительным перед другими методами при вычислении многократных интегралов, особенно при наличии сложной области интегрирования.
Недостатки метода:
• Крайне низкая скорость уменьшения погрешности.
10
Слайд №11: Экстраполяционный переход к пределу.
Численно оценивается интеграл:
J=
Z b
a
y(x)dx.
Интервал интегрирования (a, b) разбивается на n равных отрезков длинойZ h = (b − a)/n (h
— шаг интегрирования). Затем приближенно находятся площади
весь интеграл определяется суммированием
J=
n−1
X
i=0
si .
si =
xi+1
xi
y(x)dx ,
и
Расчетное значение интеграла
при этом оказывается функцией шага интегрирования: J = J(h). Чем меньше h, тем ближе
расчетное значение J(h) к точному значению интеграла.
Для более точной оценки интеграла строят зависимость J(h), и аппроксимируют ее
полиномом
J = J0 + J1 h + J2 h2 + J3 h3 + . . . .
Нулевой член J0 этого разложения — асмптотическое значение интеграла J при h → 0.
Данный метод позволяет увеличить на порядок точность расчета, т.е. если метод численного интегрирования, использованный для построения J(h), обладает погрешностью
E ∼ hn , то асимптотическое значение J0 определяет интеграл с погрешностью ∼ hn+1 .
Для метода прямоугольников E ∼ h, и зависимость J(h) при малых h хорошо аппроксимируется линейной зависимостью. Для метода трапеций (и центральных прямоугольников) E ∼ h2 , и в разложении J(h) первый коэффициент J1 необходимо приравнять нулю.
Для метода Сипсона разложение J(h) должно начинаться с члена пропорционального четвертой степени h:
J = J0 + J4 h4 + J5 h5 + . . . .
Иногда ввиду сложности интеграла, например, двойные, тройные интегралы, сложно
определить заранее характер зависимости погрешности E от величины шага интегрирования h. Тогда для экстраполяционного перехода предварительно требуется провести 4—5
расчетов при разных шагах интегрирования и определить зависимость E(h), или, что то
же самое, зависимость J(h).
11
Слайд №12: Методы интегрирования несобственных интегралов.
Z ∞
y(x)dx.
Пусть одним из пределов интегрирования является ±∞. Например: J =
a
Аналитическое интегрирование ”хвоста”.
Требуется определить асимптотическое поведение функции y(x) при x → ∞. Часто оказывается, что асимптотика функции y(x) (обозначим ее φ(x)) является легко интегрируемой.
Тогда исходный интеграл записывают в виде
J=
Z b
a
y(x)dx +
Z ∞
b
φ(x)dx ,
где b — значение x, при котором погрешность замены исходной функции y(x) ее асимптотическим пределом φ(x) пренебрежима мала. Первый интеграл считают известными
методами (Ньютона–Котеса, Гаусса–Лежандра, и т.д.), а второй вычисляют аналитически.
Недостатки метода:
• Бывают ситуации, когда невозможно представить асимптотическое поведение подинтегрального выражения
какой-нибудь простой легко интегрируемой функцией. НаZ ∞
1 −x2
e
dx таким методом не рассчитать.
пример, интеграл
x
a
Замена переменной.
От ±∞ в пределе интегрирования избавляются, переходя к новой переменной t, такой
чтобы при x → ∞, t(x) → const. Например:
J=
Вводим t = 1/x:
Z ∞
a
1 −x2
dx .
e
x
Z 1/a
1 −1/t2
dt .
e
t
0
Этот интеграл уже не представляет проблем.
J=
Недостатки метода:
• Требуемая замена переменной может слишком усложнить поведение подинтегральной
функции на одном из пределов интегрирования. Например, замена t = 1/x в интеграле:
Z ∞
Z 1/a
dx
dt
√
√
.
приводит
к
неаналитичности
в
точке
t
=
0
:
a
0
1 + x3
t4 + t
Экстраполяционный переход к пределу.
Интегрирование обрывается на некотором значении x = b, и анализируется зависимость
величины интеграла J от обратного значения b : J = J(1/b). Экстраполяция функции
J(1/b) в точку 1/b = 0 дает требуемое значение интеграла.
Недостатки метода:
• Зависимость J(1/b)
может оказаться неаналитичной в точке 1/b = 0. Например,
q
J(1/b) = J0 + ξ 1/b + . . . .
12
Слайд №13: Вычисление интегралов в нерегулярных случаях.
Нередко приходится вычислять интегралы от функций, имеющих те или иные особенности. Например, функция y(x) = x1/2 exp(−x2 ) интегрируема на участке x ∈ (0, a), но в
точке x = 0 она расходится. Для вычисления подобных интегралов применение стандартных квадратурных формул∗ неэффективно.
Методы:
1. Переход к обратной зависимости x(y) — сведение к интегралу с бесконечным пределом.
2. Аналатическое интегрирование ”хвоста”.
3. Выделение особенности: весовая функция, аддитивное выделение особенности.
Переход к обратной зависимости.
Если не составляет проблем определение обратной функции x = x(y), то искомый интеграл
может быть расчитан следующим образом:
J=
Z a
0
y(x)dx = y(a) · a +
Z ∞
y(a)
x(y)dy .
Недостатки метода:
• Необходимость обращения функции.
• Численное вычисление несобственного интеграла.
Аналатическое интегрирование ”хвоста”. Требуется определить асимптотическое
поведение функции y(x) в точке неаналитичности (при x → 0). Часто оказывается, что
асимптотика функции y(x) (обозначим ее φ(x)) является легко интегрируемой. Тогда исходный интеграл записывают в виде
J=
Z α
0
φ(x)dx +
Z a
α
y(x)dx ,
α — значение x, при котором погрешность замены исходной функции y(x) ее асимптотическим пределом пренебрежима мала. Второй интеграл считают известными методами
(Ньютона–Котеса, Гаусса–Лежандра, и т.д.), а первый вычисляют аналитически.
Недостатки метода:
• Бывают ситуации, когда невозможно представить асимптотическое поведение подинтегрального выражения
какой-нибудь простой легко интегрируемой функцией. НаZ a
пример, интеграл
(ln(x))−1 dx (0 < a < 1) таким методом не рассчитать.
0
13
Слайд №14: Выделение особенности: весовая функция.
Нередко приходится вычислять интегралы от функций, имеющих те или иные особенности. Например, функция y(x) = x−1/2 exp(−x2 ) интегрируема на участке x ∈ (0, a), но
в точке x = 0 она расходится. Для численного расчета таких интегралов подинтегральную функцию раскладывают на два сомножителя : y(x) = ρ(x)f (x), где ρ(x) — весовая
функция. Искомый интеграл представляется в виде
J=
Z b
a
ρ(x)f (x)dx .
Весовая функция должна выбираться так, чтобы она была интегрируема аналитически и
содержала всю особенность исходной функции. В приведенном примере в качестве весовой
функции разумно взять ρ(x) = x−1/2 . Далее на каждом подинтервале весовая функция интегрируется аналитически, а оставшаяся функция f (x) интегрируется численно. Другими
словами, строится квадратурная формула∗
J'
n
X
i=0
ci f (xi ) ,
весовые коэффициенты которой ci определяются интегрированием весовой функции. Так,
правило прямоугольников, вводя весовую функцию ρ(x) = x−1/2 , модифицируется следующим образом. По правилу правых прямоугольников si ' yi+1 h. С введением весовой
функции
Z xi+1
exp(−x2 )
√
dx ' ci fi+1 = ci exp(−x2i+1 ) .
si =
x
xi
где весовой коэффициент ci теперь определяется интегралом от весовой функции
ci =
Z xi+1
xi
√
√
ρ(x)dx = 2 xi+1 − 2 xi .
√
Вдали от особенности ci → h/ xi+1 , и мы приходим к обычной формуле прямоугольников.
В таблице приведены погрешности расчета по формулам прямоугольников с выделением весовой функции и без нее: E1 — правые прямоугольники, E2 — правые прямоугольники
с весовой функцией, E3 — центральные прямоугольники, E4 — центральные прямоугольники с весовой функцией.
h
10−1
10−2
10−3
10−4
E1
0.44
0.14
5e-2
1.4e-2
√
∼ h
E2
5e-2
5e-3
5e-4
5e-5
∼h
E3
0.2
6e-2
2e-2
6e-3
√
∼ h
E4
7e-4
5e-6
4e-8
4e-10
∼ h2
Достоинства метода:
• Введение весовой функции полностью восстанавливает порядок сходимости используемой квадратурной формулы, т.е. для правила правых прямоугольников E ∼ h,
трапеций — E ∼ h2 , Симпсона — E ∼ h4 , и т.д.
Недостатки метода:
14
• Необходимость подбора легко интегрируемой весовой функции ρ(x). Причем, для модификации сложных квадратурных формул интегрируема должна быть не только
сама весовая функция, но и различные произведения вида xi ρ(x).
Слайд №15: Аддитивное выделение особенности.
Нередко приходится вычислять интегралы от функций, имеющих те или иные особенности. Например, функция y(x) = x−1/2 exp(−x2 ) интегрируема на участке x ∈ (0, a), но в
точке x = 0 она расходится. Для численного расчета таких интегралов подинтегральную
функцию раскладывают на два слагаемых : y(x) = ρ(x) + f (x), где функция ρ(x) должна
выбираться так, чтобы она была интегрируема аналитически и содержала всю особенность исходной функции. В приведенном примере в качестве функции ρ разумно взять
ρ(x) = x−1/2 :
exp(−x2 )
1
exp(−x2 ) − 1
√
√
y(x) =
=√ +
.
x
x
x
Интеграл от первой функции (с особенностью) берется аналитически, а от второй — численно:
Z a −x2
√
e
−1
√
dx .
J =2 a+
x
0
По точности этот метод эквивалентен методу введения весовой функции.
Достоинства метода:
• Аддитивное выделение особенности полностью восстанавливает порядок сходимости
используемой квадратурной формулы, т.е. для правила правых прямоугольников E ∼
h, трапеций — E ∼ h2 , Симпсона — E ∼ h4 , и т.д.
Недостатки метода:
• Необходимость точного описания особенности подинтегральной функции.
15
Термины для глоссария:
Квадратурная формула — формула которая определяет приближенное значение интеграла J как сумму значений подинтегральной функции (и ее производных) с некоторыми весовыми коэффициентами cki в некоторых точках xki
J'
m X
n
X
k=0 i=0
cki y (k) (xki ) .
Точки xki называются узлами квадратурной формулы.
Полиномы Лежандра :
´n i
1 dn h³ 2
x
−
1
.
2n n! dxn
Основные свойства полиномов Лежандра:
Pn (x) =
• Pn (1) = 1, Pn (−1) = (−1)n .
• На интервале (−1; +1) полином Pn имеет n действительных корней.
• ZОртогональность :
+1
−1
Pn (x)Qk (x)dx = 0, для любого полинома Qk (x) степенью k < n.
16