Лекция 4 Файл

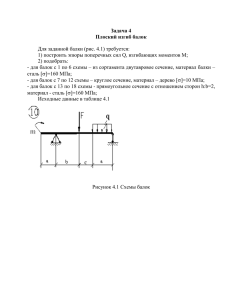
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ЛЕКЦИЯ №4
ПО ДИСЦИПЛИНЕ:
Сопротивление материалов
Раздел 6. Изгиб
6.1. Изгиб. Построение эпюр изгибающих моментов и поперечных сил.
Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки. Контроль правильности построения эпюр.
Для оценки прочности конструкции недостаточно знать внутренние силовые факторы (ВСФ) в каком-то одном сечении. Необходимо представлять, как
эти ВСФ распределены по различным сечениям, чтобы определить опасное сечение.
Опасное сечение – это поперечное сечение, в котором действуют
наибольшие ВСФ.
В простейших случаях нагружения определить опасное сечение нетрудно.
Например, на рис.6.1,а опасным сечением будет сечение А у заделки, так как
здесь действует максимальный изгибающий момент, равный МА = Р·ℓ.
а)
б)
Рис.6.1.
В более сложном случае нагружения (рис.6.1,б) сразу определить опасное
сечение достаточно трудно, так как сосредоточенный момент М и распределенная нагрузка q изгибают балку вниз, а сосредоточенная сила Р – вверх, при
этом величины изгибающего момента и поперечной силы от каждого вида
нагрузки различны.
Поэтому для сложных случаев нагружения необходимо знать закон изменения ВСФ по длине стержня. Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.
Эпюра – это график, изображающий закон изменения ВСФ по длине
стержня.
Примеры построения эпюр поперечной силы Qy и изгибающего момента
Мх (при поперечном изгибе), 6.2.
Каждая ордината эпюры представляет собой величину ВСФ в соответствующем сечении стержня. Построение эпюр выполняется по методу сечений
(РОЗУ). Из составленных на 4-ом этапе метода сечений уравнений выражаем
ВСФ для каждого силового участка стержня.
Рис.6.2.
Силовой участок – участок стержня, в пределах которого характер
нагрузки не изменяется.
Вычисляем значения ВСФ на границах силовых участков и строим эпюры, откладывая ординаты перпендикулярно оси (нулевой линии) эпюры. Ось
эпюры параллельна оси рассматриваемого стержня.
Дифференциальные зависимости при изгибе
Между изгибающими моментом М, поперечной силой Q и распределенной
нагрузкой m, q (рис.6.3,а) имеют место дифференциальные зависимости, которые могут быть установлены следующим образом.
Выделим двумя близкими поперечными сечениями элемент балки длиной dz (рис.6.3,б) и рассмотрим условия его равновесия.
а)
б)
Рис.6.3.
Так как dz мало, то погонная поперечная нагрузка q(z) и погонная моментная нагрузка m(z) на этой длине могут считаться постоянными. Запишем
уравнения равновесия элемента dz:
ΣY = 0
Qy +q(z)·dz – Qy – dQy = 0;
0
ΣMA = 0
М х  Qy  dz  q( z )  dz
 M x  dM x  0.
dz
 m( z )  dz 
2
Здесь q(z)·dz – равнодействующая распределенной нагрузки q(z), приложенная в центре тяжести (т.С) прямоугольника (рис.6.3,б)
Из первого уравнения получаем:
dQy
dz
 q( z ) .
(6.1)
Из второго уравнения, с учетом того, что q(z)·dz·dz/6 ≈ 0 как величина
более высокого порядка малости, имеем:
dM x
 Qy  m( z ) .
dz
(6.2)
Кроме того, из соотношений (6.1) и (6.6) следует, что
2
d Mx
dm( z )

q
(
z
)

.
2
dz
dz
(6.3)
При отсутствии распределенной моментной нагрузки (m(z) = 0) выражения (6.1), (6.2), (6.3) упрощаются и принимают вид:
dQy
dz
dM x
 Qy ;
dz
 q( z ) ;
d 2M x
 q( z ) .
2
dz
(6.4)
Данные дифференциальные зависимости справедливы и для случая изгиба балки в плоскости перпендикулярной к рассмотренной и используются
обычно для проверки правильности построения эпюр поперечной силы Q и изгибающего момента М.
Эпюры поперечных сил и изгибающих моментов
Рассмотрим построение эпюр Qy и Мх на примерах.
Пример 6.1. Построить эпюры на двухопорной балке с консолью
(рис.6.4).
1. Определяем реакции опор.
Для системы сил, действующих на балку, можно составить три независимых уравнения статики:
ΣХ = 0,
ΣY = 0, ΣМв = 0.
(6.5)
Из первого уравнения
ΣХ = НА = 0.
Горизонтальная реакция НА при поперечном изгибе всегда равна нулю и
на схеме нагружения ее можно не изображать.
Из уравнений:

ΣМ В  VA  4  q 2  q  2    q     0 ;
2
5
8
Y  q  3q  VD  0 ;
5
VA  q  ;
8
VD 
19
q .
8
Проверка:
ΣМ А  0
21 2 21 2
q  q  0
2
2
3q  3 ,5 
19
q  4  q 2  0
8
0 = 0,
т.е. реакции определены верно.
2. Вычисляем Qy, Мх и строим эпюры.
При растяжении – сжатии и кручении мы строили эпюры ВСФ по их
уравнениям на силовых участках.
Рис.6.4.
При поперечном изгибе мы используем другой способ, ведущий к цели
быстрее и состоящий в том, что при построении эпюр значения ВСФ определяются по границам участка и граничные ординаты эпюр соединяются линиями
на основании дифференциальных зависимостей (6.4). Этот метод иногда называют методом построения эпюр по характерным точкам. В рассматриваемом
примере это точки А, В, С, D и Е.
Эпюра Qу. Примем для внешних сил, входящих в выражения Qу по
участкам, такое правило:
Внешняя сила, совпадающая по направлению с осью Qу, входит в выражение
поперечной силы со знаком плюс, если построение идет в положительном
направлении оси z, и со знаком минус, если оно идет в противоположном
направлении (рис.6.3,б).
Положительные значения Qу будем откладывать вверх от базисной
линии, а отрицательные вниз.
Определяем значения Qу по границам участков, рассматривая левую отсеченную часть и составляя алгебраическую сумму внешних сил, действующих
на нее:
Qу
D
5
QyA  Qy  Qy  VA  q ,
В
С
8
5
11
5
19
 q  q  2   q ,
Qу  q  q  2  q  q .
D
8
8
8
8
Здесь Q у и Q у - поперечные силы в сечениях, расположенных бескоD
D
нечно близко слева от сечения D и справа соответственно.
Значения поперечной силы Qу на четвертом участке проще (меньше сил)
определять, рассматривая равновесие правой части, т.е. если вести построение
в отрицательном направлении оси z (справа налево).
Qy  q   .
Qy  0 ,
D
E
При построении эпюры Qу (рис.6.11,б) на участках I и II значения ординат Qy , Qy и Qy следует соединить линией 0-го порядка, т.к. на этих
A
В
С
участках q=0 и из зависимости (6.1) следует, что Qy = const.
При построении эпюры Qу (рис.6.11,б) на участках III и IV значения ординат Qy и Q у , Q у и Qy следует соединить линиями 1-го порядка, т.к. на
С
D
D
Е
основании дифференциальной зависимости dQy/dz=q(z)=const тангенс угла
наклона касательной к очертанию эпюры Qy на этих участках должен быть постоянен, а таким свойством обладает только линия 1-го порядка.
Эпюра Мх. Примем для изгибающего момента следующее правило:
изгибающий момент в сечении положителен, если положительна создаваемая
им кривизна упругой линии балки, и наоборот (рис.6.5,а,б). Следовательно,
знак изгибающего момента совпадает со знаком второй производной от
уравнения упругой линии в данном сечении.
а)
б)
Рис.6.5.
При направлении осей у и Мх вверх (рис.6.5, а, в) изгибающий момент от
внешнего фактора положителен, если он изгибает балку выпуклостью вниз.
Для того чтобы не ошибиться в знаке изгибающего момента, сечение, в котором он определяется, следует мыслить заделанным, а опоры отброшенными.
Для строителей важно
Эпюру Мх будем строить со стороны растянутых волокон, т.е. положительные значения М будем откладывать вниз, так как эти моменты, согласно принятому правилу знаков, вызывают растяжение нижних волокон, а отрицательные значения вверх.
Определяем величины изгибающего момента в характерных точках, составляя алгебраическую сумму моментов, действующих на отсеченную часть:
МхА = 0, так как сила VА относительно т.А плеча не имеет.
5
5
М х  q    q 2 .
В
8
8
Интенсивность распределенной нагрузки на I участке (АВ) равна нулю
(q=0), поэтому из соотношения (6.4) d6Mx /dz6=q(z) следует, что кривизна
очертания эпюры Мх равняется нулю и значения ординат МА и М В необходимо соединить прямой линией (рис.6.4, в)
5
3
М х  q 2  q 2   q 2 ,
В
8
8
5
1
М х  q  2  q 2  q 2 .
С
8
4
Так как на II участке (ВС) q = 0, а значит кривизна очертания эпюры Мх

равняется нулю и ординаты М х и М х следует также соединить прямой
В
С
линией.
Эпюру Мх на IV участке будем строить в отрицательном направлении
оси z (справа налево), рассматривая равновесие правой отсеченной части.

М D  q  .
2
МЕ = 0,
На IV участке интенсивность распределенной нагрузки q  0, так как ее
направление противоположно направлению оси у. Поэтому из (6.4) следует, что
кривизна очертания эпюры Мх отрицательна (очертание обращено выпуклостью вверх). На этом основании можно высказать правило, чрезвычайно удобное для быстрого построения очертания эпюры Мх:
очертание эпюры Мх на участке обращено выпуклостью в сторону противоположную (навстречу) направлению распределенной нагрузки – правило «зонтика».
Опираясь на это правило, соединяем значения М х и М х , М х и
С
D
D
М х кривыми линиями, обращенными выпуклостью вверх. На основании (6.4) в
Е
точке Е dMx /dz=QE=0 и кривая очертания Мх касается оси z (тангенс угла
наклона касательной в т.Е равен 0 и касательная в этой точке совпадает с
осью z).
В сечении М dM x / dz  Qy  0 и на эпюре Мх - экстремум. Для опреM
э
деления М х - экстремального значения Мх на III участке – находим zо:
5
Qy  q  q  zо  0 ;
M
8
5
zо   ,
8
тогда
2
5 
q z о2 5 
5
q5 
57 2
2
М  q2  z о   q 
 q 2     q 2     
q .
8 
8
2
8 
2  8  128
Построив эпюры Qу и Мх сформулируем их свойства, которыми следует
пользоваться для контроля правильности их построения, предполагая ось z
э
х
направленной слева направо.
Свойства эпюры Qу:
1. По dQy/dz=q(z) очертание эпюры на участке с q=0 – параллельно оси
z, с q=const – наклонно, с переменной q – криволинейно.
2. В сечении с сосредоточенной силой – скачок, равный по величине силе
и совпадающий с ней по направлению (при построении эпюры в
направлении оси z от силы, направленной вверх, - скачок вверх, а от
направленной вниз – скачок вниз).
3. Излом – в том сечении, в котором скачок в эпюре q.
Свойства эпюры Мх:
1. По d2Мх /dz2=q(z) очертание эпюры на участке с q=0 – прямолинейно, с q0 – криволинейно и обращено выпуклостью навстречу нагрузке (правило «зонтика»). По dМх /dz=Qу на участке с Qy=0 очертание
эпюры – параллельно оси z.
2. В сечении с сосредоточенной парой – скачок по величине, равный моменту пары. При построении эпюры в направлении оси z скачок вверх
(положителен), если изгибающий момент, создаваемый парой, справа
от нее – положителен (рис.6.6,а) и вниз (отрицателен), если изгибающий момент, создаваемый парой, слева от нее отрицателен (рис.6.6,б).
а)
б)
Рис.6.6.
3. Излом – в сечении с сосредоточенной силой, причем угол излома
направлен навстречу силе.
4. Экстремум – в сечении с Qy=0.
5. В шарнирных подвижных и неподвижных опорах Мх=0, если в сечениях этих опор не приложено сосредоточенных пар.
Пример 6.2. Построить эпюры на консольной балке (рис.6.7,а)
Рис.6.7.
1. Консольной называется балка, заделанная одним концом. Три компонента реакции в ее заделанном сечении находятся из уравнений (6.5). Однако,
эпюры Qу и Мх можно построить без предварительного определения реакций,
рассматривая правую отсеченную часть балки (ведя построение со свободного
конца балки, т.е. в отрицательном направлении оси z).
6.Строим эпюру Qу (рис.6.7,б)
1
QyВ  q  2q  2  q .
2
Qy  q ;
A
Значения Qy и Qy
А
В
следует соединить кривой, обращенной выпукло-
стью вниз, так как на участке АВ q 0 и увеличивается (от –6q до 0), следовательно, должен увеличиваться тупой угол касательной к кривой с осью z
(рис.6.7, б, ">'). В т.А касательная к этой кривой горизонтальна, так как
q=0.
Qy  Qy  q .
С
В
3. Строим эпюру Мх (рис.6.7, в).
М х  0,
А
М хС
1
1
2
М х В  q  2  2q  2  2  q 2 ,
2
3
3
1
1
 1 
 q  3  2q  2     2    q 2 .
2
3
 3 
В точке М (Qy = 0) имеет место экстремум М хэ и для его определения
вычисляем zо:
2q
1
qо   z о ,
 q   qо zо  0
2
2
1q 2
 q 
 zо  0 ,
zо2  2 2 ,
zо   2
2
2 1
1q
2 2 2
М хэ  q   2 
 2   2
q .
2
3
3
 
6.2. Нормальные напряжения при чистом изгибе. Прямой поперечный изгиб. Нормальные и касательные напряжения при прямом поперечном
изгибе. Проверка на прочность по главным напряжениям.
Чистый и поперечный изгиб. Формулы Навье и Журавского
Чистый изгиб. Формула Навье
Изгиб балки называется чистым, если в ее поперечных сечениях действуют только нормальные силы упругости, приводящиеся к изгибающему моменту.
Рассмотрим участок балки (рис.6.8,а) произвольного постоянного поперечного сечения (рис.6.8,б), испытывающий прямой чистый изгиб.
Чистый изгиб называется прямым, если плоскость кривизны (упругой линии) балки параллельна силовой плоскости (плоскость действия момента).
а)
б)
Рис.6.8.
Упругая линия балки – ось (z) балки после деформации в процессе изгиба.
При чистом изгибе призматической балки справедливы:
- гипотеза Бернулли (гипотеза плоских сечений):
сечения плоские и нормальные к оси балки до деформации остаются
плоскими и нормальными к ее оси после деформации;
- гипотеза о ненадавливаемости волокон:
нормальные напряжения в продольных сечениях балки равны нулю.
Справедливость данных гипотез подтверждается решениями задачи о
чистом изгибе балки методами теории упругости, наблюдениями и экспериментами.
На основании гипотезы о ненадавливаемости балка рассматривается
как совокупность растянутых и сжатых волокон, которые свободно удлиняются и укорачиваются, не оказывая давления друг на друга.
Совокупность волокон, имеющих одинаковые удлинения будем называть
слоем.
Один из крайних слоев испытывает растяжение, а другой - сжатие.
Имеется такой слой, который не растягивается и не сжимается и, следовательно, сохраняет свою длину. Этот слой называется нейтральным слоем
(Н.С).
Линия пересечения НС с поперечным сечением называется нейтральной
линией (НЛ) или нейтральной осью (Н.О) (рис.6.8,б).
Выделим из балки двумя сечениями m-m и n-n, перпендикулярными продольной оси z, элемент длиной dz (рис.6.8,а) и рассмотрим его деформацию
(рис.6.9,а),
Рис.6.9.
опираясь на гипотезу Бернулли и требование того, чтобы изгиб был прямым. В
этом элементе до изгиба слой СD имел длину нейтрального слоя АВ. После
того как балка изогнулась по окружности радиуса , нейтральный слой представляется дугой А'B'= d =АВ.
Слой СD, удаленный от НС на расстояние у, после изгиба представляется дугой C'D' окружности радиуса +у. Отсюда получаем C'D'=(+у)d.
Относительное удлинение слоя СD в процессе деформации равно

C' D' CD C' D'  A' B'   у d  d у


 .
CD
A' B'
d

(6.6)
Выражение (6.6) является аналитической записью закона плоских сечений при изгибе балки.
На основании второй гипотезы волокна балки испытывают одноосное
растяжение или сжатие. Подставив в выражение закона Гука при растяжении – сжатии выражение  из (6.6), получим

Е

у.
(6.7)
Чтобы найти положения нейтральной и силовой линий относительно
сечения и выразить  через Мх, рассмотрим равновесие левой части участка
балки, отсеченной сечением m-m (рис.6.9,б).
Уравнения
Σ  0, Σ  0, ΣМ z  0
0
удовлетворяются для отсеченной части тождественно, т.е. справедливы при
любых значениях, действующих на нее сил упругости и Мх.
Из условия равновесия отсеченной части:
 0   dF 0 .
F
Подставляя в это уравнение выражение  из (6.6), получим
Е
 уdF 
F
Е

поэтому
S x  0,
но
Е

 0,
Sx  0 .
Следовательно, нейтральная линия проходит через центр тяжести сечения – точку С (рис.6.1,б), упругая линия лежит в нейтральном слое и  будет ее радиусом кривизны (рис.6.6,а).
ΣМ у   x dF 0 .
6.
0
F
Подставляя в это уравнение выражение  из (6.6) поучим:
Е
Е
xуdF

xу  0,

F
поэтому

0
ху  0 .
0
но
Е

 0,
Следовательно, силовая (у0) и нейтральная (х) линии – главные оси поперечного сечения и поэтому взаимно перпендикулярны.
Если оси у и х – главные центральные оси сечения, то оси у0 и х, если
у0//у, то же самое главные.
Действительно, ху=0 по условию, а ус=0 из рис.6.9,б, то на основании
формулы х у  ху  аbF имеем
1 1
ху  0 .
0
Любая ось, перпендикулярная главной центральной оси, в совокупности с
ней – главные оси сечения.
Таким образом, положение изгибающего момента Мх относительно сечения при условии перпендикулярности его плоскости одной из главных центральных осей поперечного сечения, которая будет нейтральной линией, –
произвольно.
3.
М х  М х   уdF 0 .
F
После подстановки в это уравнение  из (6.6) получим
Мх 
Е
2
 у dF ,
F
2
где  у dF   x - момент инерции поперечного сечения относительно
F
нейтральной линии.
Следовательно,
1


Mx
.
E x
(6.8)
Выражение (6.8) называется основным уравнением изгиба, а произведение Ех – жесткостью поперечного сечения балки относительно оси х при изгибе.
Подставив отношение Е / из (6.3) в (6.6) получим

Мх
у.
х
(6.9)
Зависимость (6.9) есть уравнение нормальных напряжений при чистом
прямом изгибе в плоскости оси у (плоскости перпендикулярной главной центральной оси сечения х), которое носит название формулы Навье, впервые
давшего правильное решение задачи о чистом изгибе.
По аналогии, при изгибе в плоскости оси х (плоскости перпендикулярной
второй главной центральной оси сечения у), уравнение напряжений имеет вид

Му
у
 х.
(6.10)
Анализируя формулу Навье, можно констатировать, что нормальные
напряжения в сечении распределены по линейному закону и имеют максимальное значение в точках, наиболее удаленных от нейтральной линии.
Поперечный изгиб. Формула Журавского
При поперечном изгибе в сечениях балки имеет место не только изгибающий момент Мх(Му), но и поперечная сила Qу(Qx) (рис.6.10,а). Следовательно, в этом случае в поперечном сечении возникают не только нормальные ,
как это имело место при чистом изгибе, но и касательные напряжения .
При выводе расчетной формулы для  принимают следующие предположения:
1. Сечение балки имеет ось симметрии, и эта ось является силовой линией
(рис.6.10,б – ось у).
2. По прямой в сечении, параллельной нейтральной линии, касательные
напряжения равны и параллельны силовой линии (рис.6.10,в).
3. Нормальные напряжения при прямом поперечном изгибе можно определить
по формулам (6.9, 6.10), полученным для прямого чистого изгиба.
Вырежем из балки (рис.6.10,а) двумя поперечными сечениями, расстояние между которыми dz, и сечением, параллельным нейтральному слою до деформации, след которого АВ, элемент КLBA (рис.6.10,в) и рассмотрим его
равновесие.
На этом рисунке: b – ширина сечения по линии, в точках которой определяется напряжение zу (рис.6.10,б); Fотс – часть площади поперечного сечения, расположенная по одну сторону от этой линии.
По грани элемента, параллельной нейтральному слою, в силу закона парности касательных напряжений, будут действовать уz = zу, равномерно
распределенные по линии ВВ (на основании второго предположения) и по
длине dz, так как в силу малости dz  не могут измениться заметным обра-
зом.
Рис. 6.10.
Составим условие равновесия элемента, проектируя все силы на ось z
    dF  уz bdz     d dF  0,
Fотс
из которого
Fотс
 уz  bdz   ddF .
Fотс
Но по формуле (6.4)
d  dM x /  x   у , поэтому
   zу   уz 
dM x 1

  уdF ,
dz bх F
отс
где
отс
 уdF  S x - статический момент Fотс относительно нейтральной лиFотс
нии . По формуле
dM x
 Qу . Следовательно,
dz
Qу S xотс

.
х b
(6.11)
Формула (6.11) носит название формулы Журавского, впервые выполнившего общее исследование касательных напряжений при изгибе.
Формула (6.11), полученная Д.И.Журавским в 1656 г, хотя и непригодна
для определения  в любой точке произвольного сечения, дает возможность
практически точно определить значение max при условии, что h/b 6, демонстрируя этим изящное и простое инженерное решение очень трудной и чаще
точно неразрешимой математической задачи.
Задача по определению  в любой точке произвольного (несимметричного) нетонкостенного сечения методами сопротивления материалов не решается, и ее решение точно или приближенно получают методами теории упругости.
Применительно к прямоугольным сечениям первые два допущения (предположения) выполняются наиболее точно. Для прямоугольного сечения со сторонами b и h (рис.6.11) имеем:
S
отс
x
2
h 
 h   h  1  b  h
2
 b    у   ус'  b    у     у   у  
 у ,

2 
 2   2  2  2  4

3
bh
х 
.
12
Следовательно,
6 Qу  h 2 2 
  3   у 
bh  4

Рис.6.11.
и эпюра касательных напряжений изображается по высоте сечения параболой.
Наибольшие напряжения имеют место при у=0, т.е. на нейтральной линии
(НЛ).
3
2
 max   ср ;
 ср 
Qу
bh
.
Касательные напряжения характеризуют собой наличие силовых связей
между продольными слоями балки при поперечном изгибе. Эти силы препятствуют сдвигу соседних слоев друг относительно друга. Если связи между слоями нарушить, то при поперечном изгибе произойдет сдвиг слоев и несущая
способность балки существенно снизится. Например, в брусе, состоящем из n
плотно стянутых листов (рис.6.12,а), наибольшие нормальные напряжения будут равны:
 max 
M max
Pl
h 6 Pl
уmax  3
  2.
x
bh / 12 2 bh
Рис.6.12.
Если листы не связаны. То при отсутствии трения они изгибаются самостоятельно и максимальные напряжения в каждом листе равны
P
6  l
'
 max
 n 2  n max .
h
b 
n
Иными словами, связанный пакет n листов способен в первом приближении выдержать нагрузку, в n раз большую, чем несвязанный.
Расчет на прочность при прямом изгибе.
Произведем сопостовление абсолютных величин максимальных нормальных касательных напряжений, возникающих в поперечных сечениях балки, на
примере консоли с прямоугольным сечением (рис.6.6):
 max 3 Pbh 2 h

 .
 max 2bh6 Pl 4l
Рис.6.13.
Отсюда следует, что касательные напряжения при изгибе балки существенно меньше нормальных l h . Такая оценка касательных напряжений
относится ко всем балкам с массивным поперечным сечением. На тонкостенные стержни эта оценка не распространяется.
В связи с малостью величин касательных напряжений расчет на прочность при поперечном изгибе также как и при чистом изгибе массивных балок
производится только по нормальным напряжениям.
Это оправдывается еще и тем, что в опасных точках, наиболее удаленных
от нейтральной оси, касательные напряжения равны нулю.
Как следует из формул Навье (6.9, 6.10) нормальные напряжения в точках
поперечного сечения (рис.6.13,б), находящихся на одинаковом расстоянии от
нейтральной линии, равны и пропорциональны этому расстоянию. Закон распределения нормальных напряжений по сечению (эпюра ) показан на
рис.6.13,в.
Условие прочности балки имеет вид:
 
 
Mx
уmax    ,
x
M

 x уmin   .
x
 max 
 min
(6.12)
Если материал балки одинаково работает на растяжение и сжатие, то
 max 
где
Wx 
Mx
   .
Wx
(6.13)
x
.
у max
(6.14)
Здесь Wх – момент сопротивления сечения изгибу относительно оси х,
названный так потому, что отношение наибольших изгибающих моментов,
которые могут быть восприняты балками разных поперечных сечений из одинакового материала, равно отношению моментов сопротивления их поперечных сечений
М х1
М х2

Wx1
Wx 2
.
Для круга
4


R
x 
; уmax  R;
4
Для кольца
x 
 R 4
4
1 ;
4
уmax  R;
3


R
.
Wx 
(6.15)
4
Wx 
 R3
4
1  .
4
(6.16)
Для прямоугольника
3
bh
x 
;
12
b3h
у 
;
12
2
h
уmax  ;
2
b
хmax  ;
2
bh
Wx 
;
6
b2h
Wx 
.
6
(6.17)
Прочностной расчет балок при изгибе с помощью условия прочности
(6.13) может быть сведен к решению трех типов.
1. Проверка прочности (проверочный расчет)
 max 
Mx
   ,
Wx
(6.18)
т.е. проверочный расчет сводится к определению максимальных нормальных
напряжений и сравнению их с допускаемыми.
6. Подбор сечений (проектировочный расчет)
Wxтр 
Мх
 
 Wx  ,
(6.19)
т.е. проектировочный расчет сводится к определению требуемых геометритр
ческих характеристик поперечного сечения (Wх ) и сравнению их с допускаемыми [Wx] .
3. Определение допускаемой нагрузки
М х  W x  .
(6.20)
Данный расчет сводится к нахождению допускаемого изгибающего момента, который может выдержать рассматриваемая конструкция.
Максимальные нормальные напряжения max имеют место на контуре
поперечного сечения при уmax (рис.6.13,в). В силу закона парности касательное
напряжение на контуре равно нулю. Следовательно, по любой теории прочности расчетная формула для проверки прочности по наибольшему нормальному
напряжению будет иметь вид (6.18).
Условие (6.18) является необходимым условием прочности балки на изгиб в данном сечении. Во многих случаях оно же является и достаточным.
Расход материала пропорционален площади сечения F. Следовательно,
чем больше отношение Wx/F, тем больший изгибающий момент Мх выдерживает сечение с данной площадью (что равносильно с заданным погонным
весом балки) и тем меньше материала уйдет на изготовление бруса, выдерживающего заданный Мх.
Поэтому отношение Wx /F используется в качестве критерия для оценки
качества профиля.
Основываясь на этом критерии, легко убедиться, что расположение
двутавра, показанное на рис.6.14,а, выгоднее, чем показанное на рис.6.14,б.
Рис.6.14.
6.3. Элементы рационального проектирования простейших систем при
изгибе. Рациональное проектирование балок. Равнопрочные балки. Регулирование максимального изгибающего момента в балке изменением
жесткости или положения опоры, положением нагрузки.
Начнем с того, что на каждую конструкцию - простую или сложную всегда действует два типа нагрузок: полезные нагрузки и реакции самой конструкции, стремящейся уравновесить полезные нагрузки. Например, на рис.
6.15, а показана балка, опертая на две опоры по концам. В середине пролета на
нее действует сосредоточенная сила. Если бы на балку действовала только эта
сила, то балка начала бы равноускоренное движение вдоль этой силы, на самом
же деле балка неподвижна; это значит, что какие-то силы препятствуют ее движению, они уравновешивают вертикальную силу. Этими (в данном случае двумя) силами являются реакции опор. На верхних рисунках легко видеть, что такое реакция опор. Здесь полезные силы - вес грузов штанги - действуют на балку (перекладину штанги); две опоры (руки атлета) сопротивляются действию
сил. Это и есть реакция опор. Реакция опор позволяет штанге оставаться в равновесии, но если силы спортсмена сдадут, т. е. реакция опор станет меньше полезной нагрузки, штанга немедленно упадет.
Рис. 6.15. Изгибающий момент балки: а - схема сил, б - эпюра (график) изгибающих моментов, в - рациональные формы балок
Сумма проекций всех вертикальных сил на вертикальную прямую должна
быть равна нулю, если всем силам, действующим вниз, приписать знак плюс, а
силам, действующим вверх, - знак минус. Только тогда балка будет оставаться
в покое. В первом случае на рисунке слева полезная нагрузка - сосредоточенная
сила - уравновешена двумя реакциями опор. Во втором реакцией опор - мускульной силой атлета - уравновешены две полезные силы. Та из опор оказывает большее сопротивление, возле которой сосредоточено больше сил. Рис. 6.16
показывает примеры полезных нагрузок и реакций опор, а также значения максимального момента и максимального прогиба (формулы справедливы для балок и консолей, но не для стержневых систем).
В результате действия нескольких сил на балку она изгибается. Балка сопротивляется этому изгибу - в ней возникают внутренние напряжения, препятствующие дальнейшему изгибу.
Рис. 6.16. Работа консолей, балок и стержневых систем: а, в, д, е - сосредоточенные нагрузки,
б, г - равномерно распределенные нагрузки; Mmax - максимальный изгибающий момент, f максимальный прогиб
Рассмотрим другой элемент, часто встречающийся в монтировках телескопов - консоль (рис. 6.16, а, б). Консоль - это стержень, один конец которого
свободен, а второй прочно зажат (заделан) в какую-то неподвижную опору. Если нагрузить консоль, все реакции сосредоточатся в единственной опоре. Одна
из реакций будет сила, направленная навстречу полезной силе или группе сил,
и ее величина будет равна алгебраической сумме (сумме с учетом знаков) всех
полезных сил. Вторая реакция опоры - крутящий момент, который стремится
повернуть консоль навстречу вращению, вызываемому нагрузкой. На нашем
рисунке крутящий момент нагрузки действует по часовой стрелке и стремится
опрокинуть консоль. Реактивный момент, приложенный к балке со стороны
опоры, действует прочив часовой стрелки и стремится удержать консоль в покое. Сколько бы сил ни было приложено к консоли, реакция всегда будет состоять из силы и крутящего момента. Под действием внешних сил консоль изгибается. В каждом сечении консоли внутренние напряжения противостоят изгибающему моменту. Этот момент, а значит, и внутренние напряжения, минимален на конце консоли и максимален возле самой опоры. Если у балки, нагру-
женной одной силой, «опасное» сечение расположено в районе приложения силы, то у консоли практически во всех случаях опасное сечение лежит возле
опоры, поэтому чаще всего консоль имеет сечение, которое монотонно возрастает от конца консоли к опоре.
Рис. 6.17. Работа гонкого стержня на сжатие (а) и растяжение (б)р поперечный изгиб балки и
рациональные поперечные сечения балок (в)
Изгиб, который мы рассмотрели, называется поперечным. Но возможен
еще продольный изгиб. Например, на тонкую и длинную вертикальную палочку установили большой груз. Палочка стремится изогнуться, она теряет устойчивость (рис. 6.17, а). Если ее немного поддержать, не давая изгибаться, то она
может выдержать значительно больший груз, но если она не имеет дополнительных опор по длине, она теряет равновесие и изгибается. С другой стороны,
если на этой палочке тот же груз подвесить, чтобы она работала на растяжение
(рис. 6.17, б), а не на сжатие, как до сих пор, то она выдержит и значительно
большую нагрузку. Таким образом, длинные и тонкие стержни плохо работают
на сжатие, но вполне хорошо- на растяжение.
Теперь рассмотрим форму поперечного сечения балок. Во время поперечного изгиба с нагрузкой, действующей вертикально вниз, верхний пояс балки сжимается, тогда, как нижний растягивается (рис. 6.17, в). Средние же слои
деформируются мало. Внутренние напряжения в балке прямоугольного сечения
распределяются следующим образом: вдоль оси симметрии усилия равны нулю
и пропорционально возрастают по мере продвижения к крайним (верхнему и
нижнему) поясам, достигая максимума как раз на самых внешних слоях. Очевидно, что средние слои балки работают с большой недогрузкой. Поэтому
можно вместо прямоугольного сечения выбрать такое, где площадь поперечного сечения средних слоев будет меньше. Одним из самых распространенных
сечений подобного рода является двутавр (рис. 6.17, г). Почти аналогичным образом работает и швеллер (рис. 6.17, д). Вспомним, что тонкие стержни, к которым можно отнести и двутавр со швеллером, плохо работают на сжатие и хорошо на растяжение. Вспомним также, что изгибаемая балка работает своими
верхними слоями на сжатие, а нижними на растяжение, коиечяо, если сила дей-
ствует вертикально сверху вниз. Теперь ясно, что у двутавра можно резко
уменьшить сечение нижнего пояса и сохранить прежним сечение верхнего. В
пределе мы получим новое сечение, - тавр (рис. 6.17, ж). Если подобную операцию проделать и со швеллером, получится уголок (рис. 6.17, е). Существуют
равнобокие и неравнобокие уголки. У последних одна из полок в сечении
длиннее. Подчеркнем, что все эти элементы хорошо работают только в положениях, указанных на рис. 6.17, а, д, е, ж сверху.
Распределение жесткостей в стержнях системы
Для повышения жесткости без увеличения массы деталей необходимо
усиливать участки сечений, подвергающиеся при данном виде нагружения
наиболее высоким напряжениям, и удалять ненагруженные и малонагруженные
участки. При изгибе напряжены сечения, наиболее удаленные от нейтральной
оси. При кручении напряжены внешние волокна; по направлению к центру
напряжения уменьшаются, и в центре они равны нулю. Следовательно, целесообразно всемерно развивать наружные размеры, сосредотачивая материал на
периферии и удаляя его из центра.
Наибольшей жесткостью и прочностью при наименьшей массе обладают развитые по периферии полые тонкостенные детали типа коробок,
труб и оболочек.
В табл. 6.1 приведено сравнение показателей различных профилей при
изгибе. В основу сравнения положены условия равенства масс (сечений F) и
прочности (моментов сопротивления W). Увеличение прочности и жесткости
достигается последовательным применением принципа разноса материала в область действия наибольших напряжений. За единицу приняты масса, моменты
сопротивления и инерции исходного профиля 1, у которого материал сосредоточен вблизи нейтральной оси.
Придание наиболее целесообразной двутавровой формы профилям одинаковой массы (эскизы 1—5) увеличивает их прочность в 9—12 раз, а жесткость — в 40 — 70 раз по сравнению с исходным профилем. Для профилей,
одинаковых с исходным профилем прочности (эскизы 6 — 9), придание двутавровой
Таблица 6.1 Прочность, жесткость и масса профилей
формы снижает массу до 0,2 — 0,12 и повышает жесткость в 3 — 3,5 раза по сравнению с исходным профилем.
Жесткость горизонтального стержня, нагруженного вертикальными силами, пропорциональна первой степени ширины его сечения и третьей степени высоты этого сечения.
Например, увеличение ширины прямоугольного бруса в два раза увеличит его жесткость тоже в два раза. Увеличение же высоты бруса в два раза увеличит его жесткость в 8 раз (рис.
87, а).
Рис. 6.18 Жесткость стержней различного сечения: а, 6 - изменений массы при одинаковой
жесткости, в - изменение жесткости при одинаковой массе
При этом подразумевается, что все силы действуют вертикально. Если они действуют
горизонтально, то жесткость пропорциональна кубу ширины. Чтобы не было путаницы, считается, что высота сечения стержня имеет то же направление, что и направление сил. Тогда
увеличение высоты всегда значительно выгоднее увеличения ширины. В этом смысле неравнобокий уголок выгоднее устанавливать так, чтобы его большая полка была вертикальной
(ее направление совпадает с направлением сил).
Большой интерес представляют полые сечения (рис. 6.18, б, в), так как при одинаковой площади сечения полые элементы сопротивляются значительно лучше сплошных. На
этом основании существует даже мнение, что труба «работает» лучше, чем сплошной стержень того же диаметра. Это ложное мнение. Если наружный диаметр трубы и стержня одинаковы, то стержень «работает» лучше. Но если мы несколько увеличим диаметр трубы против диаметра сплошного стержня, но при этом площадь сечения возьмем для трубы меньше
(на деле это означает, что на трубу пойдет меньше материала, и она будет легче), то можно
добиться того, что они будут работать одинаково хорошо, а мы, применив трубу, сэкономим
материал и добьемся значительного облегчения. То же самое можно сказать, сравнивая
сплошной брус с полым коробом (рис. 6.18, б).
В некоторых случаях выгоднее вместо сплошного сечения взять отдельные стержни в
самых напряженных поясах (правая колонка на рис. 6.16). Так, консоль превращается в
кронштейн (рис. 6.16, а, б), а балка - в плоскую ферму (рис. 6.16, б - е). Консоль имеет растягиваемый верхний и сжимаемый нижний пояса, поэтому выгодно нижний пояс делать из до-
статочно толстого стержня, а верхний - из тонкой струны, называемой растяжкой или вантой.
Очень интересная система - ферма. Она представляет собой комбинацию стержневых треугольников, построенных так, что одна из сторон треугольника
служит основанием другого треугольника. При этом любые
нагрузки, приложенные в вершинах треугольников, вызывают в
стержнях только растяжение или сжатие и никогда изгиб. Это
позволяет применить значительно более тонкие стержни, чем в
сплошных балках при той же жесткости. Нагружение стержня в
середине его пролета в фермах нерационально и никогда не
применяется.
Здесь нужно оговориться, что это относится только к
случаю, когда стержни соединены между собой шарнирами, как,
например, показано на рис. 6.16. На практике вместо шарниров
часто применяют жесткое соединение стержней, например сваркой. В этом случае ферма работает несколько иначе, но она
остается фермой с ее основными достоинствами. На рис. 6.19
показаны различные случаи, когда разомкнутые конструкции
выгодно заменить замкнутыми, а прямоугольники из стержней системой треугольников.
Рис. 6.19. «Разомкнутые» и «замкнутые» системы
Рациональное проектирование балок
Рациональным можно считать сечение балки, которое при равной с другими
сечениями площади имеет наименьшие напряжения.
Максимальные напряжения, возникающие в
балке при действии заданной нагрузки, тем
у
меньше чем больше осевой момент сопротиву
х
h
х
h
b
b
б
a
Рис.6.20
ления сечения изгибу  m ax  M x m ax . Поэтому,
Wx
сечения с большим Wx ,будут более рациональными. Так например, прямоугольное сечение, показанное на рис.6.7а предпочтительнее использовать при изгибе под действием
вертикальной нагрузки так как осевой момент
bh 2
сопротивления сечения изгибу Wx 
для
6
него будет больше чем для этого же сечения, но повернутого на 90о (рис.6.20 б).
Анализируя эпюры напряжений, можно отметить, что на продольной линии
нормальные напряжения
равны нулю, касательные
напряжения
достигают
максимума, в крайних
волокнах, наиболее удаленных от продольной
линии, наоборот нор-
Рис.6.21
мальные напряжения достигают наибольших по модулю значений, а касательные напряжения равны нулю. Расчетная практика показала, что нормальные
напряжения, как правило, в несколько раз больше касательных. Поэтому имеет
смысл проектировать сечения так, что в зоне действия больших напряжений
находилось бы большая часть материала. Этому требованию отвечают сечения
в виде двутавровых и швеллеровых прокатных профилей, а также различные
коробчатые и кольцевые сечения.
Равнопрочные балки
В случае кручения, изгиба и сложных напряженных состояний, когда равенство напряжений по сечению принципиально недостижимо, равнопрочными
считают детали, у которых одинаковые максимальные напряжения в каждом
сечении (с учетом концентрации напряжений).
При изгибе условие равнопрочности заключается в равенстве отношения
рабочего изгибающего момента, действующего в каждом данном сечении, к
моменту сопротивления данного сечения. При кручении это условие состоит в
равенстве моментов сопротивления кручению каждого сечения детали; при
сложных напряженных состояниях — в равенстве запасов прочности.
Понятие равнопрочности применимо и к нескольким деталям, и к конструкции в целом. Равнопрочными являются конструкции, детали которых
имеют одинаковый запас прочности по отношению к действующим на них
нагрузкам. Это правило распространяется и на детали, выполненные из различных материалов. Так, равнопрочными являются стальная деталь с напряжением
200 МПа при пределе текучести σ0,2 = 600 МПа и деталь из алюминиевого сплава с напряжением 100 МПа при σ0,2 = 300 МПа. В обоих случаях коэффициент
запаса прочности равен 3. Значит обе детали одновременно придут в состояние
пластичеcкой деформации при повышении втрое действующих на них нагрузок. Независимо от этого каждая из сравниваемых деталей может еще обладать равнопрочностью в указанном выше смысле, т.е. иметь одинаковый
уровень напряжений во всех сечениях.
Рабочие нагрузки и напряжения определяют расчетом. Деталь, рассчитанная как равнопрочная, будет действительно равнопрочной, если расчет правильно определяет истинное распределение напряжений во всех ее частях, что
далеко не всегда имеет место.
Формы, требуемые условием равнопрочности, иногда трудно выполнить технологически, и их приходится упрощать. Неизбежные почти во всякой детали дополнительные элементы (цапфы, буртики, канавки, выточки, резьбы), вызывающие иногда местное усиление, а чаще концентрацию напряжений и местное
ослабление детали, также вносят поправки в истинное распределение напряжений в детали.
По всем этим причинам понятие равнопрочности деталей относительно.
Конструирование равнопрочных деталей практически сводится к приблизительному воспроизведению оптимальных форм, диктуемых условием равнопрочности, при всемерном уменьшении влияния всех источников концентрации
напряжений.
Следует иметь в виду, что при прочих одинаковых условиях жесткость
равнопрочных деталей меньше, чем жесткость деталей, имеющих хотя бы
местные повышенные запасы прочности.
Выигрыш в массе от применения принципа равнопрочности зависит от
типа нагружения и способа придания равнопрочности. Некоторое представление о порядке выигрыша в массе (а также снижения жесткости) дает пример
консольных балок нагруженных изгибающей силой Р (табл. 6.2).
Таблица 6.2 - Масса и жесткость равнопрочных консольных балок
Регулирование максимального изгибающего момента в балке изменением
жесткости или положения опоры, положением нагрузки и т. п.
С точки зрения экономии материала имеет существенное значение правильное размещение опор балок (если к этому нет препятствий по производственным или другим соображениям). Это относится и к статически определимым, и к статически неопределимым балкам*.
* Более подробно эти вопросы рассмотрены в кн.: С т е п и н П. А., Снесарев Г. А. Экономия
материалов при конструировании машин. Машгиз, 1960.
В простой балке, опертой по концам и нагруженной равномерно распределенной нагрузкой, наибольший изгибающий момент (рис. 6.22, а) имеет место посередине пролета: Мтак = ql2/8. Нетрудно убедиться, что в балке такой же
длины, но при наличии консолей (рис. 6.23, б) изгибающий момент будет
меньше.
Максимальный изгибающий момент имеет наименьшее значение тогда,
когда момент в опорном сечении равен максимальному моменту в пролете. Это
условие выполняется при длине каждой консоли 0,207l. Получающийся максимальный изгибающий момент равен Мmах =ql2/46,6.
Таким образом, надлежащим размещением опор изгибающий момент удается уменьшить примерно в шесть раз.
Рис. 6.22
Рис. 6.23
В двухпролетной статически неопределимой балке приходится иметь дело с тремя различными изгибающими моментами: МА, МВ и моментом в пролете М1 (рис. 6.22, а, б). Чтобы балка имела наименьшее сечение, постоянное по
всей длине, необходимо добиться равенства двух наибольших моментов из трех
указанных.
Также рекомендуется cтудентам доказать, что наименьшее значение максимальных изгибающих моментов получается при длине консолей равной 0,408l;
при этом M A  M Ñ 
ql 2
ql 2
, Ml 
.
12
24
Для двухпролетной балки без консолей той же длины (0,408l∙2 + 2l)
наибольший изгибающий момент будет в сечении над средней опорой (см. рис.
6.22, на рис. ошибка, можно пересчитать) M 
ql 2
.
4
Таким образом, введение двух консолей в этом случае позволяет уменьшить расчетный момент в три раза. Для трехпролетной балки без консолей
наивыгоднейшая разбивка на пролеты показана на рис. 6.24, а, для пятипролетной — на рис. 6.24, б.
Соответствующий анализ позволяет установить наивыгоднейшее размещение опор и при других видах нагрузки. Пусть, например, нагрузкой интенсивностью q нагружен любой участок балки. При загружении консолей (рис.
  q 1 a 2 / 2 (при отсутствии нагрузки в проле6.25, а) нагрузкой q1, получим M max
те).
Рис. 6.24
Рис. 6.25
При нагружении участка между опорами (рис.
  q 2 l 2 / 8 (при отсут6.25, б) нагрузкой q2 получим M max
ствии нагрузки на консолях).
Приравняв максимальные значения моментов,
имеем оптимальное значение длины консоли
à  0,5l q2 / q1 .
Необходимо отметить, что не всегда определяющим является расчет на прочность по изгибающим моментам.
В некоторых случаях размещение опор приходится производить из условия жесткости, чтобы получить
наименьшие прогибы. Например, для простой балки,
загруженной равномерно распределенной нагрузкой
(см. рис. 6.22, а), наибольший прогиб посередине
v  5ql 4 /(384 EI )  0,013ql 4 /( EI ) .
При наличии двух консолей прогиб посередине балки уменьшится (см.
рис. 6.22, б). Оптимальную длину консоли получим из условия, чтобы прогиб
на конце консоли равнялся прогибу балки посередине пролета. Воспользовавшись универсальным уравнением и опуская выкладки, которые рекомендуется
проделать cтуденту, получим оптимальную длину консоли из условия жесткости: а =0,223l.
При такой длине консоли наибольший прогиб балки составит
0,00095ql4/(EI), что меньше прогиба бесконсольной балки в 13,7 раза. Это и не
удивительно, так как в формулу прогиба длина балки входит в четвертой степени. Поэтому, например, при уменьшении длины балки в два раза прогиб балки уменьшается в 16 раз.
Отметим в качестве примера, что в железнодорожных вагонах длина консолей принимается равной а≈0,14l.
6.4. Потенциальная энергия упругой деформации балки при изгибе.
При чистом изгибе балки все волокна находятся в одноосном напряженном состоянии, поэтому удельная потенциальная энергия на основании формулы равна:
uσ 
2
.
2E
(6.21)
Нормальные напряжения  при чистом изгибе выражаются формулой
Навье:

Mx
y,
x
поэтому
M x2 2
uσ 
y .
2
2 Ex
Интегрируя последнее выражение сначала по площади поперечного сечения F, а затем по длине балки l (в целом по объему V), получаем
2

M x2 y 2
1 M x
U σ   dz 
dF  
dz .
2
2
E

2
E

x
x
0
F
0
(6.22)
При поперечном изгибе к потенциальной энергии U следует добавить потенциальную энергию U, создаваемую касательными напряжениями . Удельная энергия деформации сдвига на основании формулы (4.11) имеет следующий вид:
uτ 
2
2G
.
(6.23)
Касательные напряжения в балке определяются формулой Журавского

Qy S xотс
х b
.
В случае тонкостенной балки вместо ширины сечения b следует подставлять толщину стенки . Подставляем выражение  в формулу (6.23)
 
 
2
2


Qy2 S xотс
Qy2 S xотс
U τ   dz 
dF   dz 
bdy 
2 2
2 2
h
2
G



b
2
G



b
x
x
F
0
0
2
y
1 Q
  kx
dz,
2 0 GF
(6.24)
где F – площадь поперечного сечения балки; kх – коэффициент, учитывающий
неравномерность распределения касательных напряжений по сечению балки
(по оси х)
  dy .
отс 2
F S
kx  2  x
x h b
(6.25)
Полная потенциальная энергия деформации при поперечном изгибе балки равна сумме энергий (6.22) и (6.24), т.е.
2
Qy2 
1  M x
dz .
U 
kx

GF 
2 0  Ex
(6.26)
При изгибе балки в горизонтальной плоскости по аналогии с (6.26) можно записать:
2
2
Qx 
1  M y
U 
ky 
dz ,
GF 
2 0  Ey
ky 
где
F

2y b
S  dx .
отс 2
y
(6.27)
(6.28)
h
Значения коэффициентов для некоторых форм сечений даны в таблице
6.3:
Таблица 6.3
Форма
сечения
kx = k y
10/9
6/5
2,0
3,14
Для длинных балок, изготовленных из металла, U пренебрежимо мала по
сравнению с U, поэтому для таких балок принимают UU. В случае балок из
композиционных материалов величина U соизмерима с U, поэтому вторым
слагаемым в формулах (6.27) и (6.27) пренебрегать нельзя. Для коротких балок
U также может достигнуть существенного значения.
Потенциальная энергия деформации в общем случае нагружения
При центральном растяжении или сжатии стержня имеет место одноосное напряженное состояние. Подставив в формулу (6.21) значение нормальных напряжений

N
,
F
получим после интегрирования по объему стержня

N2
1 N 2
U   dz 
dF  
dz .
2
2
E

F
F 2 E F
0
0
(6.29)
При кручении в сечении стержня возникают только касательные
напряжения, определяемые по формуле

Мк
,
р
подставив которую в выражение (6.23) и проинтегрировав по объему, получаем
2

M к2  2
1 Mк
U   dz 
dF  
dz .
2
2
G

p
F 2Gp
0
0
(6.30)
Если стержень находится под воздействием нагрузки, вызывающей в его
сечениях шесть внутренних силовых факторов N, Mx, My, Qx, Qy, Mк, то его
потенциальная энергия деформации вычисляется как сумма выражений (6.26),
(6.27), (6.29) и (6.30). Когда рассматривается система, полученная соединением
нескольких стержней потенциальная энергия ее получается, как сумма потенциальных энергий всех стержней:
2
2
2

Qy M y
M x2
Qx2 M к2 
1 m n  N
U 

kx

ky

dz .


GF E y
GF Ep 
2 n 1 0  EF Ex
(6.31)
Интегрирование производится по длине ln каждого стержня. При этом
предполагается, что система состоит из m стержней.
Таким образом, в общем случае нагружения, формула (8.36) устанавливает зависимость потенциальной энергии деформации системы от внешних
сил, ее геометрических (F, х, у, р) и упругих (Е,G) свойств.
6.5. Определение перемещений при изгибе. Интегрирование дифференциального уравнения упругой линии. Метод уравнивания постоянных интегрирования Условия Клебша. Метод начальных параметров.
Кроме расчета на прочность элементы конструкций обязательно рассчитываются и на жесткость.
Расчет на жесткость элемента конструкции, имеющего форму стержня
(бруса), заключается в определении наибольших линейных и угловых перемещений его поперечных сечений при заданной нагрузке (рис. 5.1) и сопоставлении их с допустимыми перемещениями, которые зависят от назначения конструкции и условий ее эксплуатации. Иными словами, условие жесткости
можно выразить неравенством
 max  [ ]; max  [ ];
(5.1) (6.32)
где νmах и φmах — максимальные линейное и угловое перемещения рассматриваемого сечения, возникающие под нагрузкой; [ν] и [φ] —допускаемые значения перемещений.
Допускаемые значения перемещений зависят от конкретных требований к
конструкции и устанавливаются СНиПом.
В большинстве случаев допускаемое значение прогибов определяется из
выражения
[ν] = l/т, где l —длина пролета балки, см;
т — число, устанавливаемое нормами проектирования, которое лежит в пределах 300—1000.
Для перекрытий домов т = 500—600; для подкрановых балок т = 600—
700; для мостов т = 700.
Методическую разработку составил доцент
кафедры ПМ, к.т.н., доцент
___________________С. Полищук