Document 322967

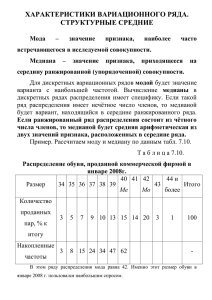
Задание 1. Классическое определение вероятности, теоремы сложения и умножения
вероятностей, формула полной вероятности.
Из 15 мальчиков и 10 девочек составляется наугад группа из 5 человек. Какова
вероятность того, что в нее попадут 3 мальчика и 2 девочки?
Решение.
m C153 C102
25!
25! 25  24  23  22  21 20!
5
P 
;
C



 53130
25
5
n
C25
5! 25  5 ! 5!20!
1 2  3  4  5  20!
15! 15 14 13  12!

 455;
3!12!
1 2  3  12!
455  45
P 
 0.385
52140
C153 
C102 
10! 10  9  8!

 45;
2! 8! 1 2  8!
Задание 2. Повторные независимые испытания.
Вероятность появления бракованной детали равна 0,008. Найти вероятность того, что из
500 случайно отобранных деталей окажется три бракованных.
Решение.
Поскольку число испытаний велико, а вероятность их появления мала для вычисления
вероятности событий используем локальную теорему Лапласа.
Pn  k  
1
  ( x)
n pq
Здесь
2
1  x2
k  n p
n  500; k  3; p  0.008; q  1  p  0.992;  ( x) 
e ; x
2
n pq
Задание 3. Дискретные случайные величины и их числовые характеристики.
Задан закон распределения случайной величины Х. Найти: 1) математическое ожидание
М(Х), 2) дисперсию D(X), 3) среднее квадратическое отклонение σ.
Х 21
25
28
31
р 0,1
0,4
0,2
0,3
Решение.
Задание 4. Непрерывные случайные величины и их числовые характеристики
Случайная величина Х задана интегральной функцией распределения F(x). Найти: 1)
дифференциальную функцию распределения f(x); 2) математическое ожидание М(х); 3)
дисперсию D(X)
0, при х≤0,
1/8х2 + 1/4х при 0 < x ≤ 2,
F(x) =
1 при х > 2
Решение. Дифференциальная функция распределения равна
0, x  0;
x 1


f ( x)  F ( x)    , 0  x  2;
4 4
x  2.
0,
Математическое ожидание и дисперсия:
2
2
 x3 x 2 
1
18
 x 1
 7
2
M ( X )   x  f ( x)dx   x     dx    x  x  dx       2   ;
40
4 4
 6
 3 2 0 43
0
0
2
2
1
49 1
49
 x 1
D( X )   x  f ( x)dx  M ( X )   x 2    dx 
   x 3  x 2  dx 

4
4
4
36
4
36


0
0
0
4
4
2
2
2
2
 x 4 x3 
49 1  16 8  49 11
   
   

4
3
36
4
4
3
36
36



0
Задание 5
Дан ряд распределения. Построить гистограмму частот, найти структурные средние:
моду и медиану, найти числовые характеристики статистического распределения:
арифметическую среднюю, дисперсию, среднее квадратическое отклонение,
коэффициент вариации, найти асимметрию и эксцесс. Сделать выводы. Проверить
эмпирическое распределение на нормальность на основе критерия Пирсона (Х2)
Урожайность с куста картофеля (в кг)
Хi
Xi+1
ni
33,1
5
3,13,2
5
3,23,3
11
3,33,4
18
3,43,5
22
3,53,6
20
3,63,7
10
3,73,8
5
3,83,9
4
Решение. Построим вариационный ряд и гистограмму частот
Xi
3
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
Интервалы
3 - 3.1
3.1 - 3.2
3.2 - 3.3
3.3 - 3.4
3.4 - 3.5
3.5 -3.6
3.6 - 3.7
3.7 - 3.8
3.8 - 3.9
Итого
Xi+1
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
Xs
3.05
3.15
3.25
3.35
3.45
3.55
3.65
3.75
3.85
n
5
5
11
18
22
20
10
5
4
100
n*Xs
15.25
15.75
35.75
60.3
75.9
71
36.5
18.75
15.4
344.6
n*Xs2
46.513
49.613
116.19
202.01
261.86
252.05
133.23
70.313
59.29
1191.1
Накопл.
Частоты
W
0.05
0.05
0.11
0.18
0.22
0.2
0.1
0.05
0.04
1
5
10
21
39
61
81
91
96
100
Здесь Xsi - середины интервалов
Гистограмма частот
25
22
20
18
15
20
11
10
5
5
5
10
5
4
0
3 - 3.1
3.1 - 3.2 3.2 - 3.3 3.3 - 3.4 3.4 - 3.5 3.5 -3.6
3.6 - 3.7 3.7 - 3.8 3.8 - 3.9
Структурные средние: мода – наиболее часто повторяющегося значения признака
Mo  X Mo  X
f Mo  f Mo 1
2 f Mo  f Mo 1  f Mo 1
где ХMo – нижнее значение модального интервала;
fMo – число наблюдений или объем взвешивающего признака в модальном
интервале;
fMo-1 – то же для интервала, предшествующего модальному;
fMo+1 – то же для интервала, следующего за модальным;
∆X – величина интервала изменения признака в группах.
Mo  3.5  0.1
22  18
 3.567
2  22  18  20
медианы – величины признака, которая делит упорядоченную последовательность его
значений на две равные по численности части
f  f
Me1
Me  X Me  X 2
f Me
,
где XMe – нижняя граница медианного интервала;
∆X – его величина (размах);
∑f/2 – половина от общего числа величин;
 1 – сумма наблюдений (или объема взвешивающего признака), накопленная до
f Me
начала медианного интервала;
fMe – число наблюдений или объем взвешивающего признака в медианном
интервале.
Me  3.5  0.1
50  39
 3.68
61
Найдем выборочное математическое ожидание.
x
 n  Xs  344.6  3.446
 n 100
Найдем выборочную дисперсии и среднее квадратичное отклонение.
Dx
n x

n
2
 x2 
1191.1
 3.4462  0.036;   Dx  0.19
100
Коэффициент вариации есть отношения среднего отклонения (линейного или
квадратичного) к средней величине.

Ë

 ëčí ĺ éí ű é ,    ęâŕ äđŕ ň č÷í ű é
x
x
где
Ë
 Xs  x n
n
i
i
 0.147
i

0.147
0.19
 0.043,  
 0.055
3.446
3.446
Найти асимметрию и эксцесс
 Xs  x 
3  
n
3
i
 Xs  x 
4  
n
i
4
ni
 0.00027 - третий центральный момент.
ni
 0.003 - четвертый центральный момент.
Коэффициент асимметрии довольно мал и отрицателен, что указывает на высокую
степень симметрии рассматриваемого распределения и незначительное его смешение
вправо. Эксцесс - мера остроты пика распределения случайной величины. Он
положителен, если пик распределения около математического ожидания острый, и
отрицателен, если пик гладкий. В нашем случае тик распределения тупой.
Проверим гипотезу о нормальности рассматриваемого распределения случайных
величин и проверим ее по критерию Пирсона.
Посчитаем теоретические вероятности попадания случайной величины в каждый
интервал по формуле
 X x 
 X x 
Pi    i 1
 i

 ,  ( x)  ô óí ęöč˙ Ëŕ ďëŕ ńŕ
 

  
Умножим, полученные вероятности на объем выборки N  100 и получим теоретические
частоты PN
. Вычислим наблюдаемый критерий Пирсона по формуле
i

2
í ŕ áë
9
 ni  PN

i
i 1
PN
i

и сравним его с критическим ęđ2   0,01; r  9  2  7   18.5
 ni
 Pi N 
PN
i
ni
2.428
6.279
12.337
18.42
20.899
18.02
11.807
5.879
2.224
5
5
11
18
22
20
10
5
4
2.725
0.261
0.145
0.010
0.058
0.218
0.277
0.131
1.418
 í2ŕ áë 
5.241
Pi N
2
Поскольку í2ŕáë  ęđ2 нет основания отвергать гипотезу о нормальном законе
распределения исследуемой случайной величине.
Гистограмма эмпирических частот и кривая теоретических
частот
25
22
20
20
18
15
11
10
10
5
5
5
5
4
0
3 - 3.1
3.1 - 3.2 3.2 - 3.3 3.3 - 3.4 3.4 - 3.5 3.5 -3.6
3.6 - 3.7 3.7 - 3.8 3.8 - 3.9
Задание 6. Проверка статистических гипотез
Используются два вида удобрений: I и II. Для сравнения эффективности были попарно
выбраны 20 участков равной площади так, чтобы пару составили участки, однородные
по плодородию. Десять участков были обработаны удобрением I, а десять, парных им, удобрением II. На соответствующих парах участков получили следующий урожай:
I
II
8,0
5,6
8,4
7,4
8,0
7,3
6,4
6,4
8,6
7,5
7,7
6,1
7,7
6,6
5,6
6,0
5,6
5,5
6,2
5,0
При уровне значимости 5% проверить гипотезу о различном влиянии использования
удобрения I и II.
Решение. Эффективность удобрения зависит, очевидно, от даваемой ими дисперсии
Выдвинем нулевую гипотезу H 0 : D( X )  D(Y ) и альтернативную H1 : D( X )  D(Y )
Построим вспомогательную таблицу
№
Xi
Yi
1
2
3
4
5
6
7
8
9
10
8
8.4
8
6.4
8.6
7.7
7.7
5.6
5.6
6.2
72.2
5.6
7.4
7.3
6.4
7.5
6.1
6.6
6
5.5
5
63.4
Сумма
Xi2
Yi2
64
31.36
70.56 54.76
64
53.29
40.96 40.96
73.96 56.25
59.29 37.21
59.29 43.56
31.36
36
31.36 30.25
38.44
25
533.22 408.64
Исправленные выборочные дисперсии равны
S x2 
2
1 
1
1
1

2
X

X

533.22

 72.22   1.326;




i
i



N 1 
N
10
 9

S y2 
2
1 
1
1
1

2
Y

Y

408.64

 63.22   0.743




i
i



N 1 
N
10
 9

Вычислим наблюдаемое значение критерия Фишера
Fí ŕ áë
S x2 1.326
 2 
 1.786
S y 0.743
Число степеней свободы равно f1  f 2  N  1  10  1  9 . Строим двухстороннюю
критическую область при уровне значимости   0.05 . Fkp  0.025,9,9   4.03
Поскольку Fí ŕ áë  Fkp данные наблюдений не позволяют отвергнуть нулевую гипотезу о
равенстве дисперсий и считать различным влияния разных удобрений.
Оценим математические ожидания двух выборок по критерию Стьюдента. Выдвинем
гипотезы H 0 : M ( X )  M (Y ); H1 : M ( X )  M (Y ) . Посчитаем наблюдаемое значение критерия.
Tí ŕ áë 
x Y
 N  1 S x2   N  1 S y2
 N 1 
7.22  6.34
 3  1.935
9 1.326  9  0.743
Tkp   0.05, f  10  10  2  18  2.1
Так как Tí ŕ áë  Tkp нет основания отвергать нулевую гипотезу о равенстве средних.
Следовательно влияние удобрений одинаково.