Моделирование полиморфных превращений в железе в

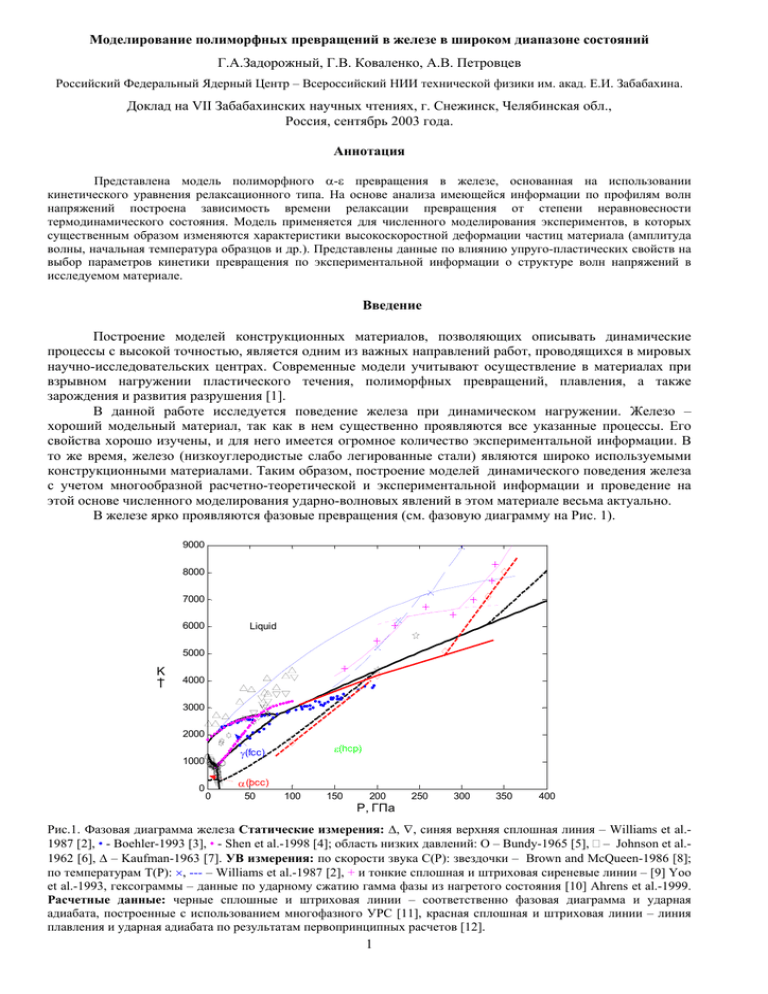
Моделирование полиморфных превращений в железе в широком диапазоне состояний
Г.А.Задорожный, Г.В. Коваленко, А.В. Петровцев
Российский Федеральный Ядерный Центр – Всероссийский НИИ технической физики им. акад. Е.И. Забабахина.
Доклад на VII Забабахинских научных чтениях, г. Снежинск, Челябинская обл.,
Россия, сентябрь 2003 года.
Аннотация
Представлена модель полиморфного α-ε превращения в железе, основанная на использовании
кинетического уравнения релаксационного типа. На основе анализа имеющейся информации по профилям волн
напряжений построена зависимость времени релаксации превращения от степени неравновесности
термодинамического состояния. Модель применяется для численного моделирования экспериментов, в которых
существенным образом изменяются характеристики высокоскоростной деформации частиц материала (амплитуда
волны, начальная температура образцов и др.). Представлены данные по влиянию упруго-пластических свойств на
выбор параметров кинетики превращения по экспериментальной информации о структуре волн напряжений в
исследуемом материале.
Введение
Построение моделей конструкционных материалов, позволяющих описывать динамические
процессы с высокой точностью, является одним из важных направлений работ, проводящихся в мировых
научно-исследовательских центрах. Современные модели учитывают осуществление в материалах при
взрывном нагружении пластического течения, полиморфных превращений, плавления, а также
зарождения и развития разрушения [1].
В данной работе исследуется поведение железа при динамическом нагружении. Железо –
хороший модельный материал, так как в нем существенно проявляются все указанные процессы. Его
свойства хорошо изучены, и для него имеется огромное количество экспериментальной информации. В
то же время, железо (низкоуглеродистые слабо легированные стали) являются широко используемыми
конструкционными материалами. Таким образом, построение моделей динамического поведения железа
с учетом многообразной расчетно-теоретической и экспериментальной информации и проведение на
этой основе численного моделирования ударно-волновых явлений в этом материале весьма актуально.
В железе ярко проявляются фазовые превращения (см. фазовую диаграмму на Рис. 1).
9000
8000
7000
6000
Liquid
5000
K,
T
4000
3000
2000
0
ε(hcp)
γ(fcc)
1000
α (bcc)
0
50
100
150
200
250
300
350
400
P, ГПа
Рис.1. Фазовая диаграмма железа Статические измерения: ∆, ∇, синяя верхняя сплошная линия – Williams et al.1987 [2], • - Boehler-1993 [3], • - Shen et al.-1998 [4]; область низких давлений: O – Bundy-1965 [5], – Johnson et al.1962 [6], ∆ – Kaufman-1963 [7]. УВ измерения: по скорости звука C(P): звездочки – Brown and McQueen-1986 [8];
по температурам T(P): ×, --- – Williams et al.-1987 [2], + и тонкие сплошная и штриховая сиреневые линии – [9] Yoo
et al.-1993, гексограммы – данные по ударному сжатию гамма фазы из нагретого состояния [10] Ahrens et al.-1999.
Расчетные данные: черные сплошные и штриховая линии – соответственно фазовая диаграмма и ударная
адиабата, построенные с использованием многофазного УРС [11], красная сплошная и штриховая линии – линия
плавления и ударная адиабата по результатам первопринципных расчетов [12].
1
Полиморфные превращения в этом материале характеризуются достаточно большими
изменениями объема. В частности, скачок объема при α-ε превращении, протекающем в железе при
нагружении волнами напряжений с амплитудой σmax≥13 ГПа [13], составляет 6%. Такие сильные
изменения термодинамических параметров приводят к изменению профилей волн, на фронте которых
образуются многоволновые конфигурации с образованием фазовых предвестников. Изучение структуры
профилей позволяет исследовать кинетику полиморфных превращений.
В настоящее время отсутствуют модели полиморфных превращений, учитывающих реальные
физические механизмы, и позволяющие адекватно описывать все особенности протекания превращений
в материалах при ударно-волновых нагрузках в широком диапазоне условий их деформирования. Для
моделирования превращений в условиях стационарных волн, формирующихся при прохождении
волнами достаточно больших (≥5 мм) расстояний, применяются кинетические уравнения
релаксационного типа [14-17]. В реальных условиях взрывных экспериментов во многих случаях
геометрия систем соответствует именно таким, достаточно большим размерам образцов, и в силу
высокой скорости превращений волны напряжений являются квазистационарными. Поэтому такие
модели могут применяться для моделирования широкого круга взрывных явлений, включая явления
сферически сходящихся и расходящихся ударных волн [18,19].
Одна из задач данной работы заключалась в развитии релаксационной модели полиморфного
превращения с включением в нее зависимостей поверхности метастабильных концентраций и
характерного времени превращения от степени неравновесности состояний. Для определения этих
зависимостей и калибровки модели использовались результаты экспериментальных измерений,
выполненных для условий, в которых в максимальной степени изменяются условия высокоскоростной
деформации частиц железа. Разработанная модель впоследствии может быть использована для
моделирования ударно-волновых явлений в других материалах с похожими свойствами.
1. Основные элементы модели
Полное описание модели ранее было приведено в [17,20].
Термодинамические свойства железа в ней рассчитываются на основе многофазного уравнения
состояния, представленного ранее в [11,21].
Упругопластические свойства материала в ней рассчитываются следующим образом.
• Область пластического течения описывается уравнением Прандтля-Рейса с законом текучести
Мизеса
S ij = 2µe ij − λS ij ,
(1)
где изменение упругой составляющей девиатора тензора скоростей деформаций e ij определяется с
использованием закона Гука, а пластической − на основе условия Мизеса J 2 ≤ Y . В соответствии с
[22] диссипативная функция записывается в виде
λ = 3µY −1 e p .
(2)
(
Здесь J 2 =
•
•
3
2
S ij S ij и ε p =
2 e pe p
3 ij ij
)
– аналоги вторых инвариантов девиаторов тензоров напряжений
и скорости пластической деформации.
Использующиеся в модели упругопластические характеристики материала – предел текучести Y и
модуль сдвига µ – зависят от его фазового состава и пористости, соответствующей образованию и
росту дефектов при расчете разрушения с использованием кинетических определяющих
соотношений.
Предел текучести сплошного однофазного материала состоит из двух составляющих, первая из
которых не зависит от скорости деформации, а зависимость его от термодинамических параметров
состояния включается через модуль сдвига [22]
) [ ( ) ( )] µ(µP, T ) ,
0
µ(P , T ) = µ 0 (1 + A P δ 1 3 − B(T − T0 )) ,
(
Y P , T , ε P , ε P = YA ε P + YR ε P , ε P
•
(4)
где δ = ρ ρ 0 , ρ0, T0 – плотность и температура при нормальных условиях.
Первая составляющая учитывает деформационное упрочнение [23]
( )
( (
YA ε P = min ⎧⎨Y0 A 1 + β ε P + ε 0 A
⎩
•
(3)
))m , YAmax ⎫⎬⎭ .
(5)
Зависимость предела текучести от скорости деформации принимается в виде степенного закона [24]
(
ε P = D ε P + ε 0 R
)C (YR )g , (YR ≤ YRmax ) .
2
(6)
•
Неупругий характер разгрузки учитывается через интерполяцию эффективного модуля сдвига [23,25]
µ eff = (M + N(1 − Z )) µ 0 ,
(7)
где константа M =
µ1
– двузначная (имеет разные значения в областях до и после перехода через
µ2
гидродинамическое состояние
J 2 = 0 ),
⎛
µ
N = ⎜⎜ 1 − M , M − 2
µ0
⎝
константа
⎞
⎟
⎟
⎠
вычисляется по двум
задаваемым значениям эффективного модуля сдвига, соответственно, в гидродинамическом
состоянии (µ1) и на обратной стороне поверхности текучести (µ2), а параметр Z определяет в
пространстве девиаторов напряжений относительное расстояние от последнего состояния на
поверхности текучести. Для плоского одномерного случая Z = 1 −
•
S ij S ijY
S ijY S ijY
=1−
S XX
Y
S XX
( S ijY − значения
девиатора в указанном выше состоянии на поверхности текучести). В модели реализован сложный
учет истории деформации в соответствии с [25].
В области смеси фаз предполагается упрощенное смесевое осреднение упругих модулей и
определение эффективного предела текучести материала
µ(P , T , ξ ) =
N
∑ ξ i µ i (P, T ) ,
(8)
i =1
) ∑ ξ i (YA,i (ε ip )+ YR ,i (ε ip , ε ip ) µ iµ(P, T) + Y0 ε 0p .
0 ,i
(
N
Y P , T , ε p , ε p , ξ =
Здесь ξi
(∑ ξ i = 1), µ , Y
i
A,i
(9)
i =1
– соответственно, весовая концентрация, модуль сдвига и часть предела
текучести i-той фазы, учитывающая деформационное упрочнение, а YR,i – вязко-пластическая часть
предела текучести. Величины уровня пластической деформации
p
εi
и скорости пластической
деформации ε ip фаз упрощенно считаются одинаковыми и совпадающими с величинами уровня
пластической деформации ε p и скорости пластической деформации ε p среды. Они определяются в
соответствии с представленными выше общими уравнениями, определяющими пластическое течение.
Зависимость модуля сдвига от термодинамических параметров состояния для ε-фазы железа построена
на основе совместного анализа [26] данных статических изотермических (Т=300 К) измерений упругих
модулей [27] и скоростей звука ударно-сжатого железа [8,28-29]. Параметры аналогичной зависимости
для γ-фазы приняты такими же, как и для ε-фазы в силу достаточно близких свойств этих фаз.
• Последний член в (9) учитывает упрочнение материала вследствие структурных изменений,
обусловленных протеканием полиморфных превращений. Величина структурного фактора ε 0p
определяется общей интегральной величиной наработки различных фаз
p
ε0 =
•
n
⎞
⎟
p
⎟ dt , ε 0 ≤ 1 ,
⎟
⎠
⎛ K
1⎜
ξ j→i
2 ⎜⎜
S
=
i
1
j∈Pi
⎝
∫ ∑∑
(10)
Y0, n – параметры модели, суммирование осуществляется по всем превращениям,
осуществляющимся в твердом состоянии.
При вычислении параметров пластического течения в области полиморфных превращений, то есть
когда
K
∑ ξ i
> 0 (К – количество твердых фаз), при определении девиатора тензора скоростей
i =1
деформаций из величины полной скорости деформаций исключается часть, связанная с
полиморфным превращением, и для изменения объема V принимается соответствующее
эффективное значение V eff
eff (P , T ) = V
(P , T ) −
V
K
∑ ξ iVi (P , T ) ,
i =1
•
(11)
где Vi (P , T ) – удельные объемы фаз.
При учете эффекта Баушингера для вычисления µeff используются смесевые параметры µ1 и µ2 (M и
N) твердых фаз:
µ1 =
K
∑
ξ i µ 1,i , µ 2 =
i =1
K
∑ ξ i µ 2 ,i .
i =1
3
Значения констант, входящих в представленные выше определяющие уравнения, которые
использовались для описания упруго-пластических свойств железа, представлены в табл. 1.
Помимо представленных выше уравнений для описания упругопластических свойств железа,
использовалась другая модель, которая интерполирует данные квазистатических и динамических
механических испытаний при скоростях деформации ε ≈10-3…103 с-1(ветвь низкоскоростной
деформации) и данные анализа ударно-волновых измерений ε ≈103…1012 с-1 (ветвь высокоскоростной
ударно-волновой деформации). Упомянутая модель представлена в докладе на конференции [30]. В
общих чертах она следует общей идее к построению широкодиапазонных моделей упругопластических
свойств материалов, которая развивается в PTW модели [31]. Можно отметить, что в этой модели эффект
Баушингера не учитывается, и в условиях высокоскоростной ударно-волновой деформации как при
нагружении, так и при разгрузке максимальные сдвиговые напряжения описываются в рамках одного и
того же закона, дающего зависимость предела текучести от скорости деформации и термодинамических
параметров железа.
Таблица 1 -
Значения параметров модели упруго-вязко-пластических свойств железа
Фаза
µ0, ГПа
α
ε
γ
82.5
68.5
68.5
-1
0.0206
0.0255
0.0255
3
7.874
8.296
8.017
-1
0.3
0.65
0.65
Т0 , К
Y0A, ГПа
300
0.65
300
0.65
300
0.65
β
0.0
0.0
0.0
ε0A
0.0
0.0
0.0
m
0.5
0.5
0.5
Y0max
A , ГПа
0.65
0.65
0.65
D1)
g2)
190
2.0
190
2.0
190
2.0
ε0R
0.0
0.0
0.0
c
0
0
0
2.5
2.5
2.5
µ1, ГПа
30
30
30
µ2, ГПа
0.0
0.0
0.0
Y0, ГПа
n
0
1
0
1
0
1
А, ГПа
ρ0, г/см
3
В⋅10 , К
YRmax ,
ГПа
Как отмечалось, для моделирования полиморфных превращений железа используются
кинетические
уравнения
релаксационного
типа.
Предполагается
выполнение
условий
термодинамического равновесия между фазами в виде равенства давлений Р и температур Т фаз и
смесевых соотношений
V=
ξ i Vi , E =
ξiEi ,
(12)
∑
∑
где Vi = Vi (P , T ) , E i = E i (P , T ) – соответственно, удельные объем и энергия i-той фазы.
Предусматривается одновременно протекание нескольких превращений из метастабильных в
данных условиях фаз в одну стабильную в данных условиях фазу [20]. Соответствующее уравнение
имеет вид
1)
В системе единиц: масса – в г, длина – в см, время – в микросекундах.
2)
Значения
параметра g=2 соответствуют универсальной зависимости
экспериментах (здесь σ max
xx - амплитуда волны).
4
(
ε p ∝ σ max
xx
)4 ,
наблюдаемой в
dξ i
=
dt
dξ j
dt
∑ J j→i ,
j∈Pi
(13)
= − J j→i , j ∈ Q i ,
где суммирование осуществляется в соответствии со списком Qi разрешенных превращений в данную
стабильную фазу. Скорости частных превращений рассчитываются на основе уравнения
J j→i
где ∆Φ ji = Φ j (P , T ) − Φ i (P , T ) ⎧ξm
ji ( ∆Φ ji ) − ξ i
⎪⎪
, ξ i < ξ m
ji ,
= ⎨ t ji ( ∆Φ ji , ξ i )
⎪
ξ i = ξ m
⎪⎩0 ,
ji ,
(14)
– разность потенциалов Гиббса фаз. Зависимости метастабильных
концентраций фаз от разности потенциалов Гиббса ξ m
ji ( ∆Φ ji ) передают метастабильные адиабаты
материала в области смеси фаз. Скорость превращений определяется характерным временем релаксации
превращения t ji ( ∆Φ ji , ξ i ) , которое также может зависеть от степени неравновесности состояния ∆Φ и,
кроме того, от концентрации фазы.
Представленная выше модель реализована в одномерном программном комплексе расчета
динамики сплошных сред Волна-97, построенном на базе разработанных ранее в РФЯЦ-ВНИИТФ
алгоритмов [32].
2. Определение параметров кинетики полиморфных превращений
Параметры кинетики полиморфных превращений в железе определялись на основе данных для αε превращения.
На Рис. 2 показан экспериментальный профиль скорости свободной поверхности железного
образца, измеренный в эксперименте 5 [28]. На этом профиле видна характерная многоволновая
структура волны напряжений в железе с выделением упругого и фазового предвестников и основной
пластической волны.
PIR Волна
1.2
1
Упругий предвестник
с/
м
к,
W
0.8
0.6
Основная пластическая Волна
0.4
Фазовый предвестник
0.2
0
1
1.1
1.2
1.3
1.4
1.5
t, мкс
1.6
1.7
1.8
1.9
2
Рис.2. Профиль скорости свободной поверхности в эксперименте 5 [28]. Ударник из железа, имеющий скорость
1.292 км/с и толщину 6.31 мм, ударяет по мишени той же толщины из этого же материала.
5
Фазовый предвестник отвечает пересечению ударной адиабатой линии равновесия α и ε фаз. На
этой волне практически превращение еще не идет. Основная часть наработки ε фазы осуществляется в
основной пластической волне, которую в дальнейшем будем обозначать P2 (по аналогии с [28]). Видно,
что она имеет достаточно большую ширину, то есть превращение осуществляется с конечной скоростью,
контролируемой временем релаксации фазового превращения.
Для доли вещества, претерпевшего α→ε превращение, принимается та же зависимость от степени
неравновесности состояний на ударной адиабате, как и в [16]
⎛ A − ∆Φ m
ξ εm = 1 − exp⎜ F
⎜
BF
⎝
⎞
⎟,
⎟
⎠
(15)
где A F - играет роль энергии активации, ∆Φ m - разность потенциалов Гиббса фаз, B F -нормировочная
постоянная ( B F = 642 Дж/моль). Пусть в некоторый момент времени на фронте волны P2 , которая
(
)
характеризуется значениями P m , T m , ξ εm , в выбранной лагранжевой частице успела наработаться
некоторая доля ε фазы (ξ ε ) , причем ξ ε < ξ εm . В моделях релаксационного типа (см. [14]) принято
считать, что скорость полиморфного превращения пропорциональна разности ξ εm − ξ ε и обратно
пропорциональна времени релаксации или характерному времени превращения τ
dξ ε ξ εm (∆Φ(P , T )) − ξ ε (P , T )
.
=
τ
dt
(16)
Если полагать, что волна P 2 является стационарной, а время релаксации - некоторая постоянная
величина, то можно получить τ , непосредственно зная “время разгона волны P2 ” t P 2 _ rise _ time , то есть
толщину фронта волны P2 в координатах (t , P ) [16].
Как известно, частица на фронте волны изменяет свое термодинамическое состояние в (P , V )
плоскости вдоль линии Рэлея. Это значит, что вещество, нагруженное волной P1 (фазовый предвестник),
начинает “двигаться” по прямой Рэлея, оказываясь, в конце концов, в состоянии, которое приписывается
волне P 2 со значениями P m , T m , ξ εm . Для этого процесса мы можем найти среднее вдоль линии Рэлея
(
значение
)
ξ εm
ξ ε , соответствующую ему величину
и, пользуясь (16), среднее значение
dξ ε
.
dt
Действительно,
∆Φ m
∫
⎛ − ∆Φ ⎞
⎟⎟ =
ξ εm = 1 − exp⎜⎜
⎝ BF ⎠
0
⎛
⎛
⎞⎞
⎜ 1 − exp⎜ − ∆Φ ⎟ ⎟d∆Φ
⎜ B ⎟⎟
⎜
⎝ F ⎠⎠
⎝
∆Φ m
ξε =
dξ ε
=
dt
С другой стороны, среднее значение
1+
(
=1+
(
ξ εm
ln 1 − ξ εm
),
1 m
ξε ,
2
ξ εm
ln 1 − ξ εm
)
−
(17)
(18)
1 m
ξε
2
.
τ
(19)
dξ ε
можно определить так:
dt
dξ ε
ξ εm
=
dt
t P 2 _ rise _ time
(20)
Приравнивая (19) и (20), получим соотношение для времени релаксации τ [16],
⎡ 1
⎤
1
1
τ = t P 2 _ rise _ time ⎢ m − +
⎥.
m
2 ln 1 − ξ ε ⎥⎦
⎣⎢ ξ ε
(
)
(21)
Время релаксации можно определять также и исходя из наилучшего описания
экспериментального профиля основной пластической волны, пользуясь оценкой (21) как
предварительным приближением. В данной работе соответствующие оценки характерного времени
превращения были получены при помощи численного моделирования экспериментов [28], отвечающих
различным амплитудам волн, которое проводилось с использованием программного комплекса Волна-97
[32]. Можно отметить, что в целом мы следовали [16], но использовали более полную модель для
описания упругопластических свойств железа. Ранее аналогичные исследования проводились в [20].
Полученная информация представлена на Рис.3, где показана зависимость характерного времени
превращения от интенсивности нагрузки. Здесь звездочки показывают значения, полученные при
6
численном моделировании, кружки – результаты оценок, выполненных исходя из (21) с использованием
данных [15] и [27], сплошная линия – подобранная аналитическая зависимость, аппроксимирующая эту
информацию.
70
60
50
)
ы
д
н
у
к
е
с
о
н
а
н(
τ
40
30
20
10
0
0
5
10
15
20
25
30
35
40
45
50
σ (ГПа)
Рис. 3. Зависимость характерного времени α-ε превращения в железе от амплитуды волны.
Видно, что время превращения существенным образом изменяется при изменении амплитуды
волны. Причем, чем больше интенсивность волны, тем меньше характерное время превращения. Это
связано с тем, что в волнах различной амплитуды достигается разная степень неравновесности, которую
принято считать движущей силой фазовых (в частности, полиморфных) превращений. Степень
неравновесности характеризуется разностью потенциалов Гиббса. В процессе деформации частиц железа
во фронте волны степень неравновесности меняется, поэтому физически более правильно будет вместо
постоянного значения τ использовать зависимость τ(P , T ) = τ(∆Φ(P , T )) . Она может быть получена
следующим образом. С помощью связи предельной концентрации ε фазы от амплитуды напряжения в
ударной волне ξ εm σ max [16] и соотношения (15), можно перейти от амплитуды напряжений к
(
)
соответствующим разностям потенциалов Гиббса
(
)
∆Φ m = ∆Φ σ max .
(22)
Все еще предполагая τ некоторой постоянной величиной для волны с определенными амплитудными
значениями σ max , T m , ξ εm , ∆Φ m , построим при помощи (22) зависимость τ ∆Φ m , аналогично
(
(
)
)
(
)
зависимости τ σ max , представленной на Рис. 3. В данной работе мы предполагаем, что соотношение
между временем релаксации и разностью потенциалов Гиббса имеет такой же вид (с точностью до
множителя), что и соотношение между средним времени τ и разностью ∆Φ m за фронтом ударной волны
τ(P , T ) = τ(∆Φ(P , T )) ∝ τ ∆Φ m (P , T ) .
(23)
Величина множителя определялась по результатам численного моделирования экспериментов
[27] по наилучшему расчетному описанию профиля основной пластической волны. Полученная в
результате зависимость τ(∆Φ(P , T )) представлена на рис. 4 вместе с зависимостью τ ∆Φ max (P , T ) .
(
)
(
7
)
70
60
50
)
ы
д
н
у
к
е
с
о
н
а
н(
τ
40
30
20
10
0
1
2
3
4
5
∆Φ /B
6
7
8
9
10
f
Рис. 4. Зависимость характерного времени превращения от разности потенциалов Гиббса. Зеленая сплошная линия
- зависимость τ(∆Φ(P , T )) , характеризующая непрерывное изменение времени релаксации превращения от степени
неравновесности состояния в частицах материала ( B F = 642 Дж/моль). Остальные обозначения аналогичны
обозначениям Рис.3 (см. текст)
Данную модель полиморфных превращений предполагалось использовать для расчетов широкого
круга взрывных экспериментов, включая эксперименты со сходящимися сферическими волнами, в
которых амплитуда волны вследствие кумуляции изменяется в широких пределах. Поэтому полученная
зависимость τ(∆Φ(P , T )) была распространена на область бόльших значений степени неравновесности,
отвечающим волнам мегабарного масштаба. Так как соответствующая информация отсутствует,
принятая экстраполяция зависимости τ(∆Φ(P , T )) (см. рис. 4) в основном основывалась на опыте
численного моделирования сферических экспериментов (см. [20]). Он показывает, что для обеспечения
физически адекватной картины процессов в этих экспериментах характерное время α-ε превращения
должно быть менее 2 нс при амплитудах волн σmax ≥ 200 ГПа, соответствующих плавлению железа на
фронте ударной волны.
Построенная таким образом зависимость времени превращения от степени неравновесности
состояний для α-ε превращения (см. рис. 4), а также поверхность метастабильных состояний
применяются для моделирования и других полиморфных превращений в железе (уравнения (13), (14)).
Соответствующая информация задается в модели в табличной форме.
3. Численное моделирование экспериментов.
В данном разделе приводятся результаты численного моделирования некоторых экспериментов,
выполненных для проверки правильности описания волновых процессов в железе.
Первая серия расчетов относится к экспериментам, представленным в [28]. Рассматривались
эксперименты, в которых нагружение образцов железа толщиной ≈6.3 мм осуществлялось ударом
железных пластин той же толщины (симметричный удар) со скоростью 1.292 м/с (эксперимент 5), 1.567
м/с (эксперимент 6), 0.9916 (эксперимент 1). Соответствующие амплитуды волн в этих экспериментах
составили, соответственно, 23.6, 30.5 и 17.4 ГПа. Результаты этих расчетов показаны на Рис.5, 6 и 7.
Данные измерений показаны кружками. Проводится сравнение с различными расчетами, которые
проводились в предположении постоянного времени превращения τ (рассматривались три варианта
τ = 10, 50 нс и наилучшее для каждого эксперимента значение, соответственно, 25 20 и 35 нс) , а также с
использованием функции τ(∆Φ(P , T )) .
8
1.2
τ = 10нс
τ = τ(∆Φ)
1.1
с/
м
к,
1
0.9
τ = 25нс
W
τ = 50нс
0.8
0.7
0.6
1.2
1.25
1.3
1.35
1.4
1.45
t, мкс
1.5
1.55
1.6
1.65
1.7
Рис.5. Профиль скорости свободной поверхности железного образца в эксперименте 5 [28]
(представлена часть профиля, относящаяся к основной пластической волне).
1.6
τ = 10нс
τ = 20нс
1.4
1.2
τ = τ(∆Φ)
1
с/
м
к,
W
τ = 50нс
0.8
0.6
0.4
0.2
0
1
1.1
1.2
1.3
1.4
1.5
t, мкс
1.6
1.7
1.8
1.9
Рис.6. Профиль скорости свободной поверхности железного образца в эксперименте 6 [28]
9
2
1
τ = 10нс
0.9
0.8
τ = 35нс
τ = 50нс
0.7
0.6
с/
м
к,
W
τ = τ(∆Φ)
0.5
0.4
0.3
0.2
0.1
0
1
1.5
t, мкс
2
2.5
Рис.7. Профиль скорости свободной поверхности железного образца в эксперименте 1 [28]
Расчеты с постоянным временем превращения аналогично данным, представленным в [16] и [20],
показывают зависимость ширины фронта основной пластической волны от характерного времени α-ε
превращения. Реальному профилю отвечают определенные значения τ , которые позволяют наилучшим
образом описать структуру этой волны. Соответствующие данные были ранее представлены на Рис. 3 и
4. Отличие наших расчетов (см. также [20]) от результатов [16] связано с использованием зависящего от
скорости деформации предела текучести, что позволяет также описать структуру фазового предвестника.
Как видно, расчеты с использованием зависящего от степени неравновесности состояния времени
превращения с такой же высокой точностью описывают экспериментальные данные.
Следующая серия расчетов относится к моделированию экспериментов [33]. В этих
экспериментах нагружение железных образцов, имевших толщину 2.46 мм, осуществлялось
алюминиевыми ударниками толщиной 2 мм при скорости столкновения 1.9 км/с. Амплитуда волны,
создаваемой в образцах, была близка к амплитуде волны в эксперименте 5 [28]. Отличие данных
измерений от измерений, представленных в [28], состоит в том, что материал образца имел различную
начальную температуру: помимо нормальной температуры образцы подогревались до 480 и 590 К.
Использование подогретых образцов позволяло изучать кинетику полиморфного превращения в области
тройной точки α-γ-ε равновесия на фазовой диаграмме железа.
Информация для рассматриваемых экспериментов представлена на Рис.8 и 9. На Рис.8 показано
сравнение расчетных и экспериментальных профилей свободной поверхности образцов. На Рис.9 дается
полученная в расчетах история изменения состояния частиц железа в Р-Т-ρ пространстве. На Рис.9
изображены также поверхности равновесных состояний и фазовые границы, соответствующие
многофазному УРС [11], которое использовалось в модели для описания термодинамических свойств
железа. Данные экспериментов показаны символом ◊. Результаты расчетов представлены сплошными
линиями, помеченными точками. Черный цвет соответствует комнатной температуре (20°С) образцов,
зеленый – температуре образцов 480°С, красный – 590°С.
10
, г/см3
Рис.8. Профили скорости свободной поверхности железных образцов в экспериментах [33]
, ГПа
,К
Рис.9. Изменение состояния частиц железа в экспериментах [33] по данным численного моделирования
11
Как видно, при нагревании образца до 480°С изменение состояния частиц железа проходит по
температурам чуть выше тройной точки α-γ-ε равновесия. При этом α-γ превращение практически
проявляется слабо, и профиль волны подобен профилю волны для образца в нормальном состоянии. Тем
не менее, протекание α-γ превращения отражается на амплитуде фазового предвестника: из-за более
сильного наклона линии α-γ равновесия по сравнению с линией α-ε равновесия, начало превращения
осуществляется при существенно более низких давлениях, и его амплитуда уменьшается. Это приводит
также к уменьшению расхождения фазового предвестника и основной пластической волны,
обнаруживаемому в экспериментальных данных и данных численного моделирования. Этот эффект
усиливается при дальнейшем повышении температуры образцов до 590°С: по давлениям начало
полиморфных превращений еще более снижается, а протяженность области превращений расширяется
как в сторону низких (α-γ), так и высоких (γ-ε) давлений. Это приводит к видимому сокращению ширины
фронта основной пластической волны. На экспериментальном профиле расщепление фронта этой волны
практически не регистрируется, а на расчетном профиле оно существенно ниже, чем в случае начальной
температуры образцов 480°С.
В целом можно отметить качественное согласие расчетных данных и результатов измерений [33]
(по многоволновой структуре волн с выделением упругого и фазового предвестника, влиянию на нее
температуры, проявлению PIR-волны и откольного сигнала, характеризующего откольное разрушение).
Во многом наблюдается также и количественное согласие (по амплитудам фазового предвестника, по
скорости деформации во фронтах волн, по скоростям волн и др.). Однако по амплитуде волны расчетные
и экспериментальные данные заметно отличаются, что требует дополнительного исследования.
В следующей серии расчетов изучалось влияние упругопластических свойств на характеристики
полиморфного α-ε превращения, определяемые в результате анализа экспериментальных профилей. На
примере данных для эксперимента 5 [28] сравнивались результаты численного моделирования,
проведенного с использованием двух моделей, одна из которых была подробно представлена в разделе 1
(см. также [17,20]), а вторая - в [30]. Результаты расчетов вместе с экспериментальными данными
представлены на Рис.10.
1.2
1
с/
м
к,
0.8
0.6
W
0.4
0.2
0
1
1.1
1.2
1.3
1.4
1.5
t, мкс
1.6
1.7
1.8
1.9
2
Рис.10. Сравнение результатов численного моделирования для эксперимента 5 из [28]. o – результаты измерений,
красная сплошная линия – расчет с упругопластической моделью, представленной в разделе 1, черная штриховая и
зеленая пунктирная линии – расчеты с упругопластической моделью [30] с задержкой и без задержки обратного
превращения
Как отмечалось в разделе 1, основное отличие двух моделей заключается в описании упругопластических свойств железа при разгрузке. Чисто вязкое поведение материала, принимаемое в
соответствие с [30], лучше описывает профили волн напряжений в железе, когда нагружение этого
материала осуществляется в области α-фазы.
12
В [16] параметры PIR-волны на экспериментальных профилях скорости свободной поверхности
железных образцов из [28] используются для определения параметров обратного полиморфного α-ε
превращения. Рис.10 показывает, что упругопластические свойства железа существенно влияют на
результат, получаемый в таких исследованиях: при использовании модели [30] более адекватное
описание профилей достигается при задании характеристик этого превращения без задержки. Это
соответствует тому, что константа А в формуле (15) должна быть равна 0, в то время как в [16] получено,
что она должна быть равной 417 Дж/моль.
Отметим, что ранее (см. предыдущую часть раздела, а также [20]) было получено, что учет
зависимости вязких свойств железа (зависимости предела текучести от скорости деформации) приводит
к более низким значениям характерных времен превращений, чем это следует из данных, полученных
без учета этой зависимости [16].
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1.
Ударные волны и экстремальные состояния вещества, под ред. В.Е. Фортова, Л.В. Альтшулера,
Р.Ф. Трунина, А.И. Фунтикова, М:, Наука, 2000, 425с.
2.
Williams, Q., Jeanloz, R., Bass, J., Svendsen, B., Ahrens, T.J., Science, 1987, vol. 236, p. 181.
3.
Boehler, R., Temperatures in the Earth’s core from melting-point measurements of iron at high static
pressures, Nature, 1993, vol. 363, pp. 534-536.
4.
Shen, G., Mao, H., Hemley, R.J., Duffy, T.S., Rivers, M.L., Melting and crystal structure of iron at high
pressures and temperatures, Geophys.Res.Lett, 1998, vol. 25, pp. 373-376.
5.
Bundy, F.P., J. Appl. Phys., 1965, vol. 36, p. 616.
6.
Johnson, P.C., Stein, B.A., Davis, R.S., J. Appl. Phys, 1962, vol. 33, p.557.
7.
Kaufman, L., Clougherty, E.V., Weiss, R.J., Acta Metall., 1963, vol. 11, p. 323.
8.
Brown J.M., McQueen R.G., Phase transition, Grunaisen parameter and elasticity for shocked iron between
77 GPa and 400 GPa, J. Geophys. Res., 1986, vol. 91, pp. 7485-7494.
9.
Yoo, C.S., Holmes, N.C., Ross, M., Webb, D.J., Pike, C., Shock temperature and melting of iron at Earth
core condition, Phys. Rev. Lett., 1993, vol. 70, pp. 3931-3934.
10. Ahrens, J.T., Holland, K.G., Chen, G.Q., Shock Temperature and Melting Point of Iron, in Shock
Compression of Condensed Matter - 1997, edited by S.C.Schmidt et al., AIP Conference Proceeding 429,
New York, 1998, pp. 133-136.
11. Dremov, V.V., Kutepov, A.L., Petrovtsev, A,V., and Sapozhnikov, A.T., Equation of state and phase
diagram of iron, in: Shock Compression of Condensed Matter - 2001, AIP Conference Proceedings #620,
editors M.D. Furnish, N.N. Thadhani, and Y. Horie, American Institute of Physics, 2002, pp.87-90.
12. Laio A., Bernard S., G.L. Chiarotti, S. Scandolo, E. Tosatti Physics of Iron at Earth’s Core Conditions,
Science, 2000, vol. 287, pp.1027-1030.
13. Bancroft, D., Peterson, E.L., and Minshall, S., Polymorphism of iron at high pressure, J. Appl. Phys., 1956,
vol. 27, pp.291-298.
14. Andrews, D. J., Calculation of mixed phases in continuum mechanics, J. Comp. Phys., 1971, vol.7, pp. 310326.
15. Swegle, J.W., J. Appl. Phys., 1990, vol. 68, No. 4, pp. 1563-1579.
16. Boettger, J. C., and Wallace, D. C., Metastability and dynamics of the shock-induced phase transition in
iron, Phys. Rev. B, 1997, vol. 55, pp. 2840-2849.
17. Petrovtsev, A,V., Bychenkov, V.A., and Kovalenko, G.V., Numerical simulation of elastic-viscous-plastic
properties, polymorphic transformations and spall fracture in iron, in Shock Compression of Condensed
Matter - 2001, AIP Conference Proceedings #620, editors M.D. Furnish, N.N. Thadhani, and Y. Horie,
American Institute of Physics, 2002, pp.591-594.
18. Забабахин Е.И., Забабахин И.Е., Явления неограниченной кумуляции // М.: Наука, 1988. – 171 с.
19. Kozlov, E.A., Experimental verification of E.I.Zababakhin hypothesis concerning limitation of energy
cumulation in the spherically converging shock wave front in medium with phase transition, in: Shock
13
Compression of Condensed Matter-1991, edited by S.C.Schmidt, R.D.P.Dick, J.W.Forbes, and D.G.Tasker.
American Institute of Physics, 1992, pp.169-172.
20. Коваленко Г.В., Петровцев А.В., Численное моделирование упруго-вязко-пластических свойств,
фазовых превращений и разрушения железа. Международная конференция “VI Забабахинские
научные чтения”, РФЯЦ-ВНИИТФ, Снежинск Челябинской обл., 24-29 сентября 2001 года.
21. Дремов В.В., Кутепов А.Л., Миронова Е.Е., Петровцев А.В., Сапожников А.Т. Построение
многофазных уравнений состояния. Международная конференция “VI Забабахинские научные
чтения”, РФЯЦ-ВНИИТФ, Снежинск Челябинской обл., 24-29 сентября 2001 года.
22. Steinberg, D.J., Lund, C.M. A constitutive model for strain rate from 10 −4 to 10 6 s-1. J.Appl.Рhys., 1989,
vol.65, No.4, pp.1528-1533.
23. Steinberg, D.J, Cohran, S.G., Guinan, M.W. A constitutive model for metals at high-strain rate.
J.Appl.Phys., 1980, vol.51(3), pp.1498-1504.
24. Tonks, D.L., Rate-dependent plasticity of copper and stainless steel under shock compression,
J. Appl. Phys., 1989, vol. 66, pp. 1951-1960.
25. Moss W. S., Glenn L. A. A Bauschinger effect model for use in large computer codes. In: Shock Waves in
Condensed Matter – 1983, edited by J. R. Asay, R. A. Graham and G. K. Straub, American Institute of
Physics, 1984, pp 133-136.
26. Задорожный Г.А. Модуль сдвига ε-фазы железа в широком диапазоне давлений и температур.
Международная конференция “VI Забабахинские научные чтения”, РФЯЦ-ВНИИТФ, Снежинск
Челябинской обл., 24-29 сентября 2001 года.
27. Ho-kwang Mao, Jinfu Shu, Guoyin Shen, Russell J.Hemley, Baosheng Li, Anil K.Singh. Elasticity and
rheology of iron above 220GPa and the nature of the Earth’s inner core. Nature, 1998, vol. 396, pp. 741743.
28. Barker, L. M., and Hollenbach, R. E. Shock wave study of the α-ε phase transition in iron. J.Appl. Phys.,
1974, vol. 45, pp.4872-4887.
29. Nguen, J.N., Holmes, N.C. Iron sound velocities in shock wave experiments up to 400 GPa. In: Shock
Compression of Condensed Matter-1999, edited by M.D.Furnish, L.C.Chhabildas, and R.S.Hixson, 2000,
American Institute of Physics, pp.81-84.
30. Сахаров М.Ю., Коваленко Г.В., Петровцев А.В., Шапоров Д.А. Модель упруго-вязко-пластических
свойств железа, описывающая сдвиговые напряжения в широком диапазоне скоростей деформации.
Международная конференция “VII Забабахинские научные чтения”, РФЯЦ-ВНИИТФ, Снежинск
Челябинской обл., 8-12 сентября 2003 года.
31. Preston, D.L., Tonks D.L., and Wallace, D.C. Model of plastic deformation for extreme conditions. J.Appl.
Phys., 2003, vol. 93, No.1, pp.211-220.
32. Куропатенко В.Ф., Коваленко Г.В. и др., Комплекс программ ВОЛНА и неоднородный разностный
метод расчета движений сжимаемых сред // Вопросы атомной науки и техники, сер. Методики и
программы численного решения задач математической физики, 1989, вып. 2, с. 9-25.
33. Скакун С.В., Разоренов С.В., Канель Г.И. Влияние температуры на реологические свойства и
полиморфные превращения в армко-железе. Труды международной конференции “Физика
экстремальных состояний вещества – 2003”, Черноголовка, 2003, с.63-65.
14