3.2. МОДЕЛИ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
3.2.1. Составление моделей
Среди операционных задач важное место занимают такие задачи,
которые имеют две характерные особенности:
– линейную зависимость между показателем эффективности и
элементами решения;
– ограничения на элементы решения, имеющие вид линейных равенств
или неравенств.
Как раньше отмечалось, такие задачи называют задачами линейного
программирования.
Задачи линейного программирования находят широкое распространение
в различных областях:
энергетике – рациональная организация электрификации районов с
помощью различных видов электростанций;
химии – составление сложных смесей с заданным составом компонентов;
сельском хозяйстве – рациональное распределение посевных площадей
под различные культуры;
нефтяной индустрии – оптимальное размещение нефтяных скважин для
увеличения добычи;
металлургии – расчет шихты для получения специальных легированных
сталей;
пищевой промышленности – составление рациона питания для
различных климатических зон и т. д.
Кроме этого, задачи линейного программирования находят применение в
построении технических систем:
– оптимальное построение сетей передачи информации;
– оптимальное распределение контрольно-измерительных средств для
управления сложными технологическими процессами;
– оптимальное управление множеством подвижных объектов;
– распознавание образов и отнесение объектов или измерительной
информации к определенным классам и т. д.
Каждая из операционных задач требует индивидуальной математической
модели, хотя многие из них достаточно хорошо разработаны и применимы к
целым классам родственных проблем. Процесс создания математической
модели, помимо предварительного исследования размерности задачи, требует
ответа на три основных вопроса:
– чем можно управлять для поиска оптимального решения;
– как выразить математически цель управления;
– что мешает достичь наибольшей эффективности управления.
Ответ на первый вопрос заключается в определении управляемых
переменных, которые могут изменяться для поиска оптимального решения. От
правильности выбора управляемых переменных в значительной степени
2
зависит корректность разрабатываемой модели. Неправильное решение этого
вопроса может погубить весь проект.
Второй вопрос предполагает математическую запись целевой функции,
где бы фигурировали управляемые переменные с коэффициентами,
отражающими оценку преимущества одних
и нежелательность других
вариантов для достижения наибольшей эффективности.
Третий вопрос предусматривает учет технологических или технических
ограничений, присутствующих в рассматриваемой операции. При этом
управляемые переменные должны быть включены в математические
соотношения, задающие нормы или пропорции, связанные с организацией
операции, и общие ограничения на ресурсы или оборудование, используемые
для оптимизируемого производства.
3.2.2. Задача о составе смеси
В
металлургической,
химической,
нефтеперерабатывающей,
сельскохозяйственной и других отраслях составляются различные смеси,
которые должны удовлетворять определенным требованиям.
Имеется n продуктов, обозначаемых P1, …, Pj, …, Pn, стоимостью
соответственно c1, …, cj, …, cn , и каждый из продуктов содержит m одинаковых
компонентов, но в разных пропорциях, как приведено в таблице.
1
…
…
i
m
P1 a11 ... a1i ... a1m
c1
x1
Pj a j1 ... a ji ... a jm
cj
xj
Pn a n1 ... a ni ... a nm
cn
xn
b1
…
bi
…
bm
Из этих продуктов необходимо составить смесь, чтобы она содержала
1-й компоненты не менее b1 ,…, m-й компоненты не менее bm . Это будут
условия, предъявляемые к смеси, и, следовательно, ограничения в модели.
Требуется так составить смесь, чтобы при соблюдении условий она имела
минимальную стоимость, что для модели будет целью.
Во-первых, выбираются управляемые переменные. Обозначим
количество продуктов
P1, …, Pj, …, Pn , входящих в состав смеси,
соответственно x1, …, xj, …, xn, что и будет управляемыми переменными. Тогда
общая стоимость смеси будет определяться соотношением, которое и
необходимо минимизировать для выполнения цели:
n
F c1 x1 c j x j c n x n c j x j min .
j 1
(3.1)
3
Условия составления смеси в математической форме запишутся по
каждой из компонент в виде
a11 x1 ... a j1 x j ... a n1 x n b1 ,
a1i x1 ... a ji x j ... a ni x n bi ,
a1m x1 ... a jm x j ... a nm x n bm .
(3.2)
Это и есть ограничения, накладываемые на решение.
Поэтому задача может быть сформулирована следующим образом:
выбрать такие неотрицательные значения переменных x1, …, xj, …, xn ,
удовлетворяющие
n
a x b , i 1, m ,
j 1
ji
j
(3.3)
i
при которых линейная функция этих переменных обращается в минимум
n
F c j x j min .
(3.4)
j 1
Переменные модели по смыслу задачи не могут принимать
отрицательные значения, поэтому дополнительно накладывается условие
неотрицательности решения
x j 0, j 1, n .
3.2.3. Задача о загрузке оборудования
На предприятии имеется два вида оборудования в количестве N1 и N2,
которое может производить четыре типа продукции Т1 , Т2 , Т3 , Т4, но в
различных объемах, определяющихся производительностью станков aij,
обозначающей, что i-й станок занят производством j-го вида продукта. Каждая
единица продукции приносит предприятию доход с1 , с2 , с3 , с4 соответственно.
Предприятию установили план по каждому виду продукции в размере b1 , b2 , b3
, b4 .
Все данные сведены в таблицу
Количество
оборудования
N1
N2
Доход на
единицу
продукции
План (не менее)
Вид продукции
Т1
а11 (x11)
а21 (x21)
Т2
а12 (x12)
а22 (x22)
Т3
а13 (x13)
а23 (x23)
Т4
а14 (x14)
а24 (x24)
с1
с2
c3
с4
b1
b2
b3
b4
4
Во-первых, для составления модели выбираются управляемые
переменные, именно xij – число станков i-го типа, занятого производством j-го
продукта. Требуется так распределить загрузку оборудования производством
различного вида продукции, чтобы выполнить план и получить при этом
максимальную прибыль. Эта цель в модели может быть представлена в виде
F ( x11a11 x 21a 21 )c1 ( x12 a12 x 22 a 22 )c 2 ( x13 a13 x 23 a 23 )c3 ( x14 a14 x 24 a 24 )c 4 max , (3.5)
что соответствует максимизации прибыли.
При решении должны соблюдаться естественные ограничения по
количеству задействованных в производстве станков:
x11 x12 x13 x14 N1 ,
x 21 x 22 x 23 x 24 N 2 ,
(3.6)
т. е. сумма единиц оборудования не должна превышать имеющегося на
предприятии.
И второе ограничение – записанное в математическом виде условие,
чтобы план по всем видам продукции был выполнен:
a11 x11 a 21 x 21 b1 ,
a x a x b ,
12 12
22 22
2
a13 x13 a 23 x 23 b3 ,
a14 x14 a 24 x 24 b4 .
(3.7)
Приведенные соотношения для целевой функции и ограничений (3.6) и
(3.7) вместе с условием неотрицательности xj 0 составляют математическую
модель задачи о загрузке оборудования.
3.2.4. Задача о распределении ресурсов
Предприятие имеет определенные ресурсы, например: R1 – рабочая сила;
R2 –сырье; R3 – оборудование и т.д. в количестве b1, …, bi , …, bm единиц, а
стоимость единицы каждого ресурса d1, …, di , …, dm . С помощью этих
ресурсов производятся изделия Y1, …, Yj, …, Yn, так что для изготовления
единицы изделия Yj необходимо aij единиц ресурса Ri. Каждая единица изделия
Yj может быть реализована по цене cj. Количество производимых единиц
изделия ограничено спросом, и рынок не может поглощать более чем kj единиц
изделия Yj .
Требуется определить, какое количество различных изделий необходимо
произвести, чтобы получить максимальную прибыль. Это цель операции. Для
удобства условия сведены в таблицу.
R1
Ri
Rm
Y1 a11
Yj a j1
Yn an1
b1
d1
ai1
a m1
aij
am j
ain
am n
bi
di
bm
dm
C1 x1K
Cj 1 xj
Cn Kj xn
Kn
5
В качестве управляемых переменных очевидно выбираются
производимые изделия в количестве x1 ,…, xj ,…, xn соответственно.
Условия спроса накладывают ограничения:
x1 k1 , …, xj kj , …, xn kn .
Ресурсов должно хватить на производство, следовательно,
a11x1 ... a1 j x j ... a1n xn b1 ,
ai1 x1 ... aij x j ... ain xn bi ,
a m1 x1 ... a m j x j ... a m n xn bm ,
(3.8)
или в свернутом виде
n
a x b , i 1, m .
j 1
ij
j
(3.9)
i
Теперь выражается прибыль от реализации изделий, которая
представляет собой разность между продажной ценой и себестоимостью
n
m
j 1
i 1
F x j (c j aij d i ) max ,
(3.10)
m
где a ij d i - себестоимость единицы изделия Yj ;
i 1
m
(c j a ij d i ) – чистая прибыль от реализации единицы изделия Yj .
i 1
3.2.5. Задача о перевозках (транспортная задача).
Имеется m складов, n пунктов потребления, связанных сетью дорог с
определенными тарифами перевозок. При этом сij – стоимость перевозки
единицы груза из i-го склада в j-й пункт потребления. На складах имеются
запасы однородного товара в количествах a1 ,…, ai ,…, am. Пункты потребления
подают заявки, соответственно, на единицы товара b1 ,…, bj ,…, bn . Необходимо
составить план перевозок, т. е. Указать, с какого склада, в какие пункты
потребления и какое количество товаров нужно отправлять, чтобы заявки были
выполнены, а общие расходы на перевозки были бы минимальными.
В качестве управляемых переменных берется количество товара,
направляемого из i-го склада в j-й пункт потребления xij . Если между
соответствующими пунктами нет перевозок, то принимается xij = 0.
m
n
i 1
j 1
Заявки считаются выполнимыми, если ai b j , т. е. сумма заявок не
превышает всех запасов. Это будет дополнительным условием задачи.
Количество взятого с каждого склада товара не должно превышать
имеющегося запаса, поэтому
x11 x1 j x1n a1 ,
xi1 xij xin ai ,
x m1 x mj x mn a m ,
или в свернутом виде
6
n
x a , i 1, m .
j 1
ij
i
(3.11)
Заявки, поданные пунктами потребления, должны быть выполнены,
следовательно:
m
x i1 b1 ,
i 1
m
x in bn ,
i 1
m
или xij b j , j 1, n .
(3.12)
i 1
Полная стоимость перевозок, которую по условиям задачи необходимо
минимизировать, включает суммарную стоимость перевозок между всеми
складами и всеми пунктами потребления, т. е.
m
n
F cij xij min .
(3.13)
i 1 j 1
Это и будет целевая функция транспортной задачи.
3.3. ОСНОВНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Несмотря на многообразие математических моделей, существуют
способы перехода от всех частных задач к основной задаче линейного
программирования. Она формулируется следующим образом.
Для переменных x1 , …, xn найти такие неотрицательные значения
xj 0 , j 1, n ,
(3.14)
которые обращали бы в максимум целевую функцию
n
F c j x j max
(3.15)
j 1
и удовлетворяли системе равенств
n
a x b , i 1, m .
j 1
ij
j
i
(3.16)
Основную задачу линейного программирования можно представить в
матричном виде
F = C X max ,
(3.17)
AX=B,
(3.18)
X 0,
(3.19)
где C = [c1 , …, cj , …, cn] – матрица-строка коэффициентов целевой функции;
a11 a1n
A
– матрица коэффициентов системы ограничений;
a m1 a mn
7
b1
T
– матрица-столбец коэффициентов правых частей
B b , ... b , ... b
1
i
m
b m
ограничений, записанная в транспонированном виде;
x1
T
– матрица-столбец переменных.
X x , ... x , ... x
1
j
n
x n
В частных задачах может потребоваться не максимизация, а минимизация
целевой функции. В этом случае для сохранения алгоритма максимизации
решается задача при целевой функции с обратным знаком, т. е. если F min min,
то в задаче берется F max = – Fmin .
Если в частной задаче в системе ограничений есть неравенства, то от них
можно перейти к ограничениям-равенствам и, наоборот, от равенств можно
перейти к неравенствам в случае исследования результатов решения.
Например, a11 x1 + … + a1n xn b1 (a11 x1 + … + a1nxn b1 ) , или
a11 x1 + … + a1n xn – b1 0.
Вводится новая переменная xn+1, равная левой части неравенства
xn+1 = a11 x1 + … + a1n xn – b1 .
На эту новую переменную также
накладывается условие
неотрицательности xn+1 0 . Перенеся новую переменную в левую часть
неравенства, получим
a11 x1 + … + a1n xn – xn+1 = b1 или (a11 x1 + … + a1n xn + xn+1 = b1 ).
В целевую функцию дополнительные переменные входят с нулевыми
коэффициентами:
F = c1 x1 + … + cn xn – 0 xn+1 max.
В частой задаче требование неотрицательности может накладываться не
на все переменные. Например, xj не ограничено в знаке. В этом случае вводят
замену
xj = xj – xj , xj 0, xj 0.
Это увеличивает число переменных, но позволяет избежать трудностей
при анализе решения двойственных задач.
Чтобы решить задачи линейного программирования надо ответить на три
вопроса:
1) Имеет ли задача допустимые решения, т. е. совместна ли система
ограничений?
2) Имеет ли целевая функция экстремум?
3) Каков этот экстремум, при каких значениях переменных достигается?
Набор чисел X = [x1, …, xj , …, xn], удовлетворяющий условиям (3.14) и
(3.16), называется допустимым решением.
Решение, при котором линейный функционал (3.15) достигает
экстремума, называется оптимальным решением.
При анализе системы может оказаться:
8
1) условия (3.16) противоречивы, т. е. не существует набора чисел,
удовлетворяющих этим условиям, в этом случае задача не имеет решения;
2) условия (3.16) непротиворечивы, но F не имеет экстремума, тогда
задача тоже неразрешима.
Если
a a1n
A 11
–
a m1 a mn
матрица
системы,
то
a a1n
AР 11
a m1 a mn
b1
–
bm
расширенная матрица системы, у которой добавлен столбец свободных членов.
Если в матрице произвольным образом выбрать k строк и k столбцов, то
элементы, лежащие на их пересечении, образуют квадратную матрицу k – го
порядка.
Определитель ее называется минором k – го порядка матрицы А.
Рангом матрицы называется наивысший порядок миноров матрицы,
отличных от нуля.
Теорема Кронекера-Капелли утверждает, что для того, чтобы система
AX=B имела хотя бы одно решение, т. е. была совместна, необходимо и
достаточно, чтобы ранг матрицы системы был равен рангу расширенной
матрицы.
Таким образом, тот общий ранг, который имеют матрица системы и
расширенная матрица, составляет ранг системы и представляет собой число
независимых уравнений в системе.
Если r–ранг системы, то r n(число неизвестных),r m (число уравнений).
Возьмем r = m и далее везде будем предполагать, что m – число
независимых уравнений.
Рассматриваются обычно два случая, когда число уравнений равно или
меньше числа переменных.
В первом случае, когда число уравнений равно числу переменных (m=n),
система имеет единственное решение x1 ,…, xj ,…, xn . В линейном
программировании это редкий случай и практического значения не имеет.
Во втором случае число уравнений меньше числа переменных, т. е. m < n.
Это наиболее распространенный вариант задач линейного программирования.
В этом случае, если система ограничений совместна, она имеет бесконечное
множество решений. При этом части переменных, число которых определяется
разностью между m и n, можно придавать произвольные значения. Они
называются свободными переменными. Остальные переменные можно выразить
через свободные, и они называются базисными переменными.
Если хотя бы одна переменная отрицательная, то решение задачи
недопустимо.
9
4. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
4.1. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ГРАФИЧЕСКИМ
МЕТОДОМ
Для удобства геометрического представления основной задачи линейного
программирования (3.14) – (3.16) рассматривается случай, когда число
переменных n на 2 больше числа уравнений m, т. е. n–m=2. Это означает, что
две переменные можно взять в качестве свободных, например x1 , x2, а
остальные сделать базисными и выразить их через свободные. Получится
система ограничений вида
x3 31 x1 32 x 2
x x x
4
41 1
42 2
4
...............................
(4.1)
x n n1 x1 n 2 x 2 n ,
где ij – пересчитанные коэффициенты матрицы системы,
i – правые части ограничений.
Свободные переменные можно взять в качестве осей координат; x1, x2 0,
следовательно, графическое решение будет находиться в первом квадранте
координатной плоскости (x1 , x2). Остальные базисные переменные также
должны удовлетворять требованию неотрицательности x3 0, x4 0, …, xn 0.
Это означает, что если взять предельное значение равенства нулю, например x3
= 0, то из системы (4.1) следует, что это будет в выбранной системе координат
уравнение прямой: 31 x1 + 32 x2 + 3 = 0.
При этом по одну сторону от прямой будет полуплоскость, в которой
x3 <0, а по другую – x3 >0, что соответствует требованию неотрицательности.
Интересующую полуплоскость переменной x3 = 0 удобно отметить
штриховкой, как это показано на рис. 4.1. Аналогично можно построить и
остальные прямые x4 = 0, …, xn = 0 с выделением штриховкой допустимой
стороны.
x2
В результате часть плоскости,
x4=0
принадлежащая всем полуплоскостям,
xn=0
образует
область
допустимых
решений (ОДР), представляющую
xj=0
ОДР
собой выпуклый многоугольник. Если
хотя бы одна из полуплоскостей не
x>
3 0
перекрывает область допустимых
x1
решений, как, например, xj на рис. 4.1,
то задача не имеет решения.
x<
x3=0
x5=0
3 0
Теперь необходимо рассмотреть
графическое нахождение из числа
Рис. 4.1
10
допустимых решений оптимального решения, обращающего в максимум или в
минимум (в зависимости от условий задачи) целевую функцию
Fmax = c1 x1 +…+ cj xj +…+ cn xn .
Подставив в указанную формулу значения базисных переменных,
выраженных через свободные (4.1), получим линейную функцию, зависящую
только от свободных переменных с возможным свободным членом 0:
F = 1 x1 + 2 x2 + 0 .
(4.2)
Данное уравнение можно построить в тех же координатах, что и область
допустимых решений. Очевидно, наклон полученной прямой будет
определяться величинами и знаками коэффициентов 1 и 2 . От величины 0
будет зависеть смещение этой прямой относительно начала координат. Для
предварительного построения прямой, соответствующей целевой функции
(4.2), можно выбрать произвольное значение 0 , которое в процессе
графического решения задачи все равно будет изменяться. Остается определить
направление сдвига рассматриваемой прямой для оптимизации функционала.
Если коэффициенты положительны, т. е. 1 >0 , 2 >0, то из (4.2) следует,
что, например, для максимизации следует перемещать прямую целевой
функции в сторону увеличения x1 , x2 (вправо и вверх) до тех пор, пока она не
достигнет крайних значений границы области допустимых решений, как
показано на рис. 4.2. Значения координат этой точки и будут оптимальными
значениями x10 , x20.
x2
X2
Fmax
x20
1 >0
2 >0
ОДР
x1
F
X2
X1
1 <0
2 >0
1 <0
2 <0
X1
1 >0
2 <0
x10
Рис. 4.2
Рис. 4.3
Для вычисления значений остальных переменных оптимальные значения
x1 , x 20 подставляются в систему (4.1):
0
x 30 31 x10 32 x 20 3
.
.................................
x 0 x 0 x 0
n1 1
n2 2
n
n
Так же вычисляется оптимальное значение целевой функции
Fm0 ax 1 x10 2 x 20 0 .
11
В случае других знаков коэффициентов направления перемещения
максимизируемой целевой функции приведены на рис. 4.3.
Графический метод решения применим для случая двух свободных
переменных, уже при трех свободных переменных его использование
затруднено.
4.2. СВОЙСТВА ОСНОВНОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
При решении задач линейного программирования используются
некоторые общие свойства, которые можно проиллюстрировать на примере
задач с двумя свободными переменными.
1) Решение основной задачи линейного программирования, если только
оно существует, не может лежать внутри области допустимых решений, а
только на ее границах.
2) Решение основной задачи линейного программирования может быть не
единственным, если прямая, определяющая целевую функцию, параллельна той
стороне области допустимых решений, где функционал достигает максимума. В
этом случае задача имеет бесконечное множество оптимальных решений, как
показано на рис. 4.4.
X2
X1
Рис. 4.4
3) Основная задача линейного программирования может не иметь
решений даже в случае существования области допустимых решений, если
область не ограничена в направлении оптимальности (рис. 4.5).
X2
X1
Рис. 4.5
4)
Решение
основной
задачи
линейного
программирования,
максимизирующее или минимизирующее целевую функцию, всегда
достигается в одной из вершин области допустимых решений. Решение,
12
лежащее в одной из вершин области допустимых решений, называется
опорным или базисным решением.
5) Чтобы найти оптимальное решение, достаточно перебрать все
вершины или опорные точки области допустимых решений и выбрать из них
ту, где функционал достигает экстремума.
6) Если число свободных переменных основной задачи линейного
программирования при n базисных равно двум и решение основной задачи
существует, то оно всегда достигается в точке, где, по крайней мере, две из
переменных обращаются в нуль. Например, x4 = 0, x3 = 0 в точке К (рис. 4.6).
x4=0
x5=0
x2
L
x6=0
K
ОДР
x1
x3=0
Рис. 4.6
Случай, когда в оптимальном решении обращается в нуль не две, а более
переменных, называется вырожденным (точка L на рис 4.6).
4.3. ИССЛЕДОВАНИЕ ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Нахождение оптимального решения является лишь первым этапом
решения задачи ЛП. Наибольший интерес представляет знание того, в каких
пределах можно менять входные параметры без существенного отклонения от
найденного оптимального решения.
Послеоптимизационный анализ решения предусматривает проведение
исследования чувствительности модели задачи ЛП к изменению:
1) значений коэффициентов правых частей системы ограничений – bi,
2) значений коэффициентов целевой функции – cj,
3) значений коэффициентов матрицы системы – aij.
Использование понятия двойственности позволяет рассмотреть первые
две задачи анализа. При геометрическом представлении задачи ЛП можно
исследовать чувствительность решения к изменению всех видов
коэффициентов.
Необходимо отметить, что при исследовании чувствительности
графического решения задачи ЛП к варьированию исходных параметров
фактически определяются пределы изменения коэффициентов , и в
13
выражениях (4.1) и (4.2), а не a,b,c соответственно. Но поскольку система (4.1)
и выражение (4.2) выводятся из предыдущих формул, то соответствующие
коэффициенты однозначно связаны между собой. Поэтому в дальнейшем будем
говорить об изменении a,b,c.
4.3.1. Исследование чувствительности решения к изменениям
коэффициентов правых частей ограничений
Основная цель анализа чувствительности в данном случае состоит в том,
чтобы выявить допустимые пределы изменения правых частей ограничений bi
(i=1,m) в (3.16) при неизменности найденного оптимального решения. Т.е. для
каждого из коэффициентов bi необходимо определить интервал (biMIN , biMAX),
для всех значений которого система (3.16) была бы совместна и ее решение не
менялось. При этом полагаем, что остальные (m-1) коэффициентов сохраняют
свои первоначальные значения.
Для исследования чувствительности решения задачи ЛП к изменениям
коэффициентов правых частей ограничений анализируется ОДР на
возможность параллельного переноса прямой, соответствующей i-му
ограничению ОДР и не примыкающей к оптимальной вершине, т. е. вершине, в
которой функционал достигает оптимального значения.
Считаем, что точка D
X2
соответствует
оптимальному
решению (рис. 4.7). Границы
C
D
0
ОДР, примыкающие к вершине
X2
D, то есть CD и DE, не могут
B
быть перенесены без изменения
ОДР
координат D, а значит, и
оптимального решения.
A
Границу
ВС
можно
переместить параллельно самой
себе в сторону начала координат
F
E
или наоборот. Параллельный
0
X1
перенос ВС означает изменение
FMAX
X1
коэффициента bi уравнения этой
прямой. При этом оптимальное
Рис. 4.7
решение не изменится до того
момента, пока ВС не подойдет к точке оптимальности D. Таким образом
определится минимальное значение коэффициента biMIN . Значение
коэффициента biMAX можно найти, перемещая ВС от начала координат до тех
пор, пока точки С и В максимально не приблизятся друг к другу. В этом
предельном случае прямая ВС, соответствующая i-му ограничению, фактически
«выйдет» за пределы ОДР, образованной оставшимися (m –1) ограничениями.
Аналогично находятся пределы изменения коэффициента bi+1 уравнения,
определяющего прямую AF. Значение коэффициента возрастает при
параллельном переносе AF от начала координат, пока данная прямая вплотную
не подойдет к точке В, поскольку при исследовании на чувствительность число
14
вершин ОДР не должно уменьшаться. Нижний предел изменения
коэффициента bi+1 можно определить, перемещая AF к началу координат до
совмещения точек А и F.
Так, предельно возможный перенос границы ОДР без нарушения
оптимальности определяет пределы варьирования соответствующего
коэффициента bi. При желании можно исследовать чувствительность решения к
изменению сразу нескольких значений констант в правых частях ограничений
исходной задачи. Для этого необходимо одновременно осуществить
параллельный перенос двух или более границ ОДР (не примыкающих к
оптимальной вершине). Причем интервалы изменения одного и того же
коэффициента b могут быть различными, в зависимости от набора
перемещаемых прямых и порядка, в котором производится перенос.
Пример.
Рассмотрим графическое решение конкретной задачи и исследуем его на
чувствительность к изменениям коэффициентов правых частей ограничений.
Исходные данные:
5 x1 4 x 2 20
2 x 3x 24
1
2
x1 3x 2 3
x1 8
x1 , x2 0,
FMAX = 3x1+2x2 .
Область допустимых решений данной задачи OKLMNP представлена на
рис. 4.8. Как видно из рисунка функционал достигает своего максимума в
вершине М:
FMAX (x1 , x2 )= FMAX (8.0; 2.7)=29.33.
K/L/
L
L//
K
M
FMAX
N
K//
O
P
Рис. 4.8
15
Для исследования на чувствительность выбираем одну из границ ОДР,
исключая LM и MN, примыкающие к оптимальной вершине. Выбранная прямая
KL, соответствующая 1-му ограничению системы, на рисунке помечена
стрелками. Начальное значение коэффициента: b1 = 20.
Для нахождения верхнего предела изменения коэффициента необходимо
осуществить параллельный перенос прямой KL вверх от начала координат. В
итоге точки К и L практически совместятся, и ОДР изменится: OK’L’MNP.
Максимальное значение составит b1MAX = 31.50.
Минимальное значение коэффициента можно найти при перемещении
прямой KL параллельно самой себе до совмещения точек О и К. При этом ОДР
будет представлять собой многоугольник OK”L”MNP, а значение
коэффициента станет равным b1MIN = 0.50.
В обоих случаях точка М осталась оптимальной вершиной, и ее
координаты не изменились, а значит, не изменилось оптимальное решение.
Аналогично проводится исследование на чувствительность к изменению
коэффициента b ограничения, соответствующего прямой NP. Границы ОДР,
совпадающие с осями координат (в данном примере OP и OK), не участвуют в
исследовании на чувствительность, поскольку они определяются не
ограничениями системы, а условием неотрицательности значений переменных.
4.3.2. Исследование чувствительности решения к изменениям
коэффициентов матрицы системы ограничений
Анализ чувствительности решения к изменениям коэффициентов
матрицы системы сводится к отысканию допустимых пределов изменения
коэффициентов aij (i = l , m ; j = l , n ) при сохранении оптимальности найденного
решения.
Как уже было сказано выше, при геометрической интерпретации решения
задачи ЛП уравнение вида xj =j1x1+j2x2+j задает прямую на плоскости,
представляющую собой некоторую границу ОДР. Соотношение коэффициентов
при неизвестных, т. е. j1 , j2, определяет наклон этой прямой. Тогда для
исследования чувствительности решения к изменениям коэффициентов
ограничений необходимо графически определить пределы поворота (наклона)
соответствующей границы ОДР. Границы ОДР, примыкающие к оптимальной
вершине, не рассматриваются, потому что изменение их положения повлияет
на оптимальное решение.
Для задачи, ОДР которой изображена на рис. 4.9, оптимальное решение
будет находиться в вершине В. Можно исследовать возможность поворота
только границы CD. Причем CD не должна перекрывать оптимальную
вершину, чтобы полученное решение оставалось неизменным.
16
Пределы
изменения
коэффициентов
целесообразно
X2
исследовать поочередно. Для
B
X20
этого поворот прямой нужно
выполнять относительно точек ее
пересечения с осями координат.
A
C
В данном случае для
исследования
одного
ОДР
коэффициента
необходимо
осуществить
предельный
поворот относительно точки D.
При
наклоне
CD
влево
O
предельное
(например,
X10
D
X1 минимальное)
значение
FMAX
коэффициента будет достигнуто,
когда точка С максимально
Рис. 4.9
приблизится к оптимальной
вершине. Наклон в противоположную сторону возможен до пересечения точки
С с осью абсцисс, где определится максимальное значение данного
коэффициента.
При исследовании другого коэффициента поворот нужно производить
относительно точки пересечения CD с осью ординат. Пределы наклона и
соответствующие им значения коэффициента определяются точно так же, как
описано выше.
Можно исследовать и одновременное изменение обоих коэффициентов
при сохранении оптимальности полученного решения, например, осуществляя
предельные повороты относительно точки С.
Пример.
Необходимо провести исследование на чувствительность решения к
изменению коэффициентов матрицы системы для задачи со следующими
условиями:
x1 4 x 2 22
2 x x 16
1
2
x1 5 x 2 4
x 2 8
x1 , x2 0,
FMAX = 7x1 + 6x2 .
На рис. 4.10 сплошными серыми линиями изображена ОДР данной
задачи. Функционал достигает оптимального значения в точке С, являющейся
одной из вершин ОДР. Найдем пределы изменения коэффициентов при
переменных уравнения: – x1 + 4x2 22, соответствующего границе АВ.
17
A/B/
B
B//
A/B/
B
C
C
A
A
FMAX
FMAX
A//
Рис. 4.10
Рис. 4.11
Сначала рассмотрим поворот АВ относительно точки А. Так как данная
точка расположена на оси ординат, то при изменении наклона АВ будет
варьироваться только значение коэффициента 11 при неизвестной x1. При
повороте АВ против часовой стрелки абсолютная величина 11 возрастает и в
предельном случае достигает значения 11 = -229.16, в результате чего форма
ОДР соответствующим образом изменяется – со стороны прямой АВ новая
ОДР будет ограничена штриховыми черными линиями (рис. 4.10). Таким же
образом при повороте АВ по часовой стрелке получим 11 = -0.85, а прямая АВ
займет новое положение, обозначенное на рис. 4.10 черной сплошной линией.
Поворот границы АВ относительно точки В приведет к одновременному
изменению обоих коэффициентов 11 и 12 (рис. 4.11). Аналогично
приведенному выше будем иметь:
- поворот против часовой стрелки: 11 = -91.85, 12 = 117.56; новая ОДР
со стороны АВ ограничена черной сплошной линией;
- поворот по часовой стрелке: 11 = -0.85, 12 = 2.81; ОДР со стороны
АВ ограничена штриховыми черными линиями.
4.3.3. Исследование чувствительности решения к изменениям
коэффициентов целевой функции
Анализ чувствительности полученного решения к варьированию
коэффициентов функционала, как и в предыдущих случаях, предусматривает
нахождение пределов изменений коэффициентов cj при постоянстве
оптимального решения.
При графическом представлении решения задачи ЛП изменение
коэффициентов в выражении целевой функции соответствует изменению ее
18
наклона. Возможные пределы поворота целевой функции определяются
наклоном границ ОДР, примыкающих к оптимальной вершине.
Более подробно рассмотрим на конкретном примере.
Примеры.
Задана система ограничений
2 x1 3x 2 24
x1 3x 2 3
6 x1 6 x 2 30
1x 4 x 24
2
1
x1 , x2 0,
и следующая целевая функция: FMAX = 2x1 + 5x2 .
Графическое решение задачи приведено на рис. 4.12. Оптимальной
является вершина В. Примыкающие к ней границы ОДР АВ и ВС определяются
4-м и 1-м ограничениями соответственно.
Найденное оптимальное решение
остается прежним, если наклон прямой
FMAX будет меньше или равен наклону
прямой ВС, но больше или равен
B
A
наклону прямой АВ. На рис. 4.12
показаны
предельно
возможные
положения прямой FMAX (когда наклон
FMAX и границы одинаков) {1} и {2}.
{2}
C
В случае {1} выражение для
целевой функции совпадает с левой
{1}
частью 1-го ограничения, то есть
FMAX
FMAX=2x1+3x2.
Если
уменьшать
коэффициент при x2 или (и) увеличивать
при x1, оптимальное решение перейдет в
точку С. В случае {2} выражение для
Рис. 4.12
функционала по аналогии принимает
вид: FMAX = -x1 + 4x2. При увеличении (по модулю) коэффициента при x1 и (или)
уменьшении при x2 оптимальной станет вершина А, и, следовательно,
оптимальное решение изменится.
Также в рамках исследований на чувствительность к варьированию
исходных параметров задачи ЛП можно определить, какие из коэффициентов
задачи целесообразно изменять для увеличения оптимального значения
функционала.
В качестве примера рассмотрим задачу об использовании сырья
(ресурсов).
Задача формулируется следующим образом: предприятие располагает
запасами сырья трех видов – s1 , s2 , s3 соответственно в количествах b1 , b2 , b3 .
Из этого сырья может производиться два вида изделий P1 ,P2 . Известны: aij –
количество единиц si -го вида сырья, идущего на изготовление единицы Pj – го
вида изделия, и cj – доход, получаемый от реализации одной единицы каждого
вида изделия. Все указанные величины представлены в таблице.
19
Прибыль от продажи изделия P1 равна 3 условным единицам, от продажи
одного изделия P2 – 2 условным единицам.
Необходимо составить такой план выпуска продукции, при котором
доход предприятия от реализации изделий обоих видов был бы максимальным.
Вид сырья
Запас сырья
Расход сырья на изделие
P1
P2
s1
b1 = 21
A11=3
A12 =1
s2
b2 = 30
A21 =2
A22 =2
s3
b3 = 16
A31 =0
A32 =3
Для построения математической модели задачи введем следующие
обозначения: x1 – количество единиц изделия вида P1 , x2 – количество единиц
изделия вида P2 , которое может выпустить предприятие.
Исходя из условий задачи составляем систему ограничений и выражение
для целевой функции:
3x1 x 2 21
2 x1 3x 2 30
2 x 16
2
x1 , x 2 0,
FMAX = 3 x1 +2 x2 .
Полученная система ограничений устанавливает, что количество сырья,
расходуемое на изготовление всех изделий, не может превысить имеющихся на
предприятии запасов.
На рис. 4.13 представлено графическое решение рассматриваемой задачи.
Функционал достигает своего максимального значения FMAX (4.7; 6.9) = 27.86 в
вершине С. Точка оптимальности С лежит на пересечении прямых ВС и CD.
Поэтому изменения расположения этих
прямых (параллельный перенос или
A
B
наклон) приведут к изменению
координат точки С, а следовательно, и
C
значения целевой функции.
Исследуем, какие из исходных
параметров данной задачи влияют на
увеличение оптимального значения
функционала.
Прибыль,
которую
получит
FMAX
предприятие, зависит от объемов
выпуска продукции видов P1 , P2 .
D
O
Производство
продукции
ограничивается
запасами
сырья.
Рис. 4.13
Причем из анализа ОДР
20
следует, что лимитирующими (дефицитными) ресурсами будут только b1 , b2 ,
поскольку они являются коэффициентами правых частей ограничений,
задающих прямые CD и ВС соответственно. Прямая АВ непосредственно не
примыкает к оптимальной вершине, поэтому изменение в определенных
пределах количества ресурса b3 (см. пункт 4.3.1.) не повлияет на оптимальный
выпуск продукции. Это свидетельствует о том, что данный ресурс используется
не полностью, т. е. имеет место скрытый запас этого вида сырья. Дефицитные
ресурсы при производстве расходуются в полном объеме. Увеличивая запас
любого из них, предприятие получает возможность скорректировать план
выпуска так, чтобы в результате повысить свой доход.
Геометрически вышесказанное интерпретируется следующим образом:
коэффициент b1 или b2 получает приращение, соответствующая прямая
смещается параллельно самой себе в направлении от начала координат (в
данном примере), что приводит к изменению положения точки оптимальности,
а значит и значения целевой функции (оно увеличивается). Пределы
варьирования b1 и b2 определяются аналогично пункту 4.3.1. (Исследование
чувствительности решения к изменениям коэффициентов правых частей
ограничений.)
Поскольку в рассматриваемой задаче нас интересует максимизация
функционала, то целесообразно определить только верхние пределы изменения
b1MAX, b2MAX . Тогда, исследуя коэффициенты поочередно, получаем:
b2MAX = 32.5, FMAX (4.4; 7.9) = 28.93 (b1 = 20);
b1MAX = 44.5, FMAX (14.8; 0.1) = 44.64 (b2 = 30).
Полученные значения b2MAX = 32.5 и b1MAX = 44.5 означают, что,
увеличивая запасы соответствующего ресурса сверх указанных пределов,
предприятие уже не получит дополнительной прибыли при остальных
неизменных параметрах производства.
Так же можно исследовать поведение целевой функции при
одновременном варьировании b1 и b2 .
21
5. РЕШЕНИЕ ЗАДАЧИ ЛП СИМПЛЕКСНЫМ МЕТОДОМ
5.1. АЛГОРИТМ ПОИСКА ОПТИМАЛЬНОГО РЕШЕНИЯ
Симплексный метод или метод последовательного улучшения плана
основан на идее перехода от одного базисного решения в вершине
многоугольника допустимых решений к другому базисному решению, более
близкому к оптимальному.
Задача ЛП формулируется следующим образом:
n
задана система ограничений aij x j bi , i 1, m, x j 0 .
j 1
n
Требуется найти максимум целевой функции F c0 c j x j max .
j 1
Предполагается, что ранг системы равен числу уравнений m и меньше
числа переменных n.
Пронумеруем переменные таким образом, чтобы вначале шли свободные
переменные, а далее базисные переменные:
x , x 2 ,..., x k , x k 1 , x k 2 ,..., x k i ,..., x n .
1
свободные
k nm
базисные m
Выразим базисные переменные и целевую функцию через свободные
переменные:
k
x k i bi aij x j , i 1, m ,
j 1
k
F c0 c j x j max .
j 1
Для удобства использования алгоритма свободные переменные выделяем
с отрицательными знаками:
k
xk i bi aij ( x j ), i 1, m ,
(5.1)
j 1
k
F c j ( x j ) c0 max .
(5.2)
j 1
Решение задачи осуществляется в симплексной таблице, у которой
каждая строка соответствует уравнению из (5.1):
x k i a i1 ( x1 ) ... a ij ( x j ) ... a in ( x n ) bi .
Т. е. каждая строка симплекс-таблицы соответствует базисной
переменной, а каждому столбцу соответствует свободная переменная xj и
выделен столбец свободных членов (правых частей ограничений) bi . Внизу
помещена строка целевой функции F.
Базисные
22
Свободные переменные
-x1 …
-хj …
xk+1
a11
a1j
…
xk+ i
ai1
ajj
…
xn
am1
amj
c j c j
F
c1
-xk
a1k
aik
amk
ck
b
b1
…
bi
…
bm
c0
Решение системы, полученное приравниванием свободных переменных к
нулю, называется базисным (опорным) решением.
Таким образом, в таблице записано следующее опорное решение:
xk+1=b, …, xk+i=bi , …, xn=bm ,
xj=0, j = 1, k .
При этом, как видно, целевая функция будет равна F=c0 .
Рассматриваются только те свободные переменные, которые входят в
целевую функцию с отрицательным коэффициентом, например c j c j .
Увеличение такой переменной ведет к увеличению максимизируемой целевой
функции. Если сохранить за остальными свободными переменными нулевое
значение и начать увеличивать xj , то целевая функция будет увеличиваться, что
и нужно для оптимизации.
Переменную xj можно увеличивать до тех пор, пока одна из базисных
переменных xk+1,…,xn не обратится в ноль, например xk+i. Дальше увеличивать xj
нельзя, т.к. переменная xk+i станет отрицательной, т.е. нарушится условие
неотрицательности (xk+i 0). А когда произойдет обращение в ноль базисной
переменной можно установить из соотношений:
xk+1 = b1 - a1j xj ,
…
xk+i = bi - aij xj ,
(5.3)
…
xn = bm - amj xj ;
F = c0 + cj xj .
Причем нас интересуют только те уравнения, в которых коэффициент
aij>0, т.к. при aij 0 с увеличением xj соответствующая базисная переменная
никогда не обратится в ноль.
Базисная переменная обратится в ноль, когда выполнится
соотношение x j
bj
aij
(i 1, m) .
Быстрее всех обратится в ноль та базисная переменная, для которой
отношение
bj
a ij
является
минимальным.
Это
отношение
называется
симплексным отношением. Остальные базисные переменные при этом будут
еще положительны.
23
Коэффициент аij называется генеральным коэффициентом или
разрешающим элементом.
Выведем переменную xj из числа свободных и сделаем ее базисной (т.к.
раньше установили, что ее можно увеличить для оптимизации), а вместо нее
введем переменную xk+i, которая быстрее других базисных переменных
обратится в ноль. Теперь необходимо выразить целевую функцию F и новый
набор базисных переменных (в который вошла xj) через набор новых
свободных переменных, куда вошла xk+i. Допустим, надо поменять переменную
xj на yi при разрешающем элементе aij в таблице 1 и получить новую таблицу 2.
Исходная таблица 1
-x1 …
-xj
y1 a11 …
a1j
…
yi
… …
a i1 …
…
а ij
Таблица 2
y1
-x1
a11+ai1(-a1j/aij)
…
…
-yi
-a1j/aij
…
xj
…
ai1/aij
…
…
…
1/aij
Эти преобразования осуществляются в симплексной таблице по
следующему алгоритму:
1. В таблице 1 выделяется разрешающий элемент на пересечении i-й
строки и j-го столбца (aij).
2. В таблице 2 разрешающий элемент заменяется на обратную величину.
3. Все остальные элементы разрешающей строки i делятся на
разрешающий элемент.
4. Все элементы разрешающего столбца j делятся на разрешающий
элемент и меняют знак на противоположный.
5. Все остальные элементы, не принадлежащие разрешающим столбцу и
строке, вычисляются по правилу «прямоугольника». Мысленно выделяется
прямоугольник, в котором подлежащий пересчету элемент и разрешающий
элемент образуют одну из диагоналей. Из произведения этих элементов
вычитается произведение элементов, образующих другую диагональ
прямоугольника, а результат делится на разрешающий элемент.
Сам алгоритм нахождения оптимального решения включает следующие
операции.
1. Просматривается строка целевой функции F, и если среди ее
коэффициентов, не считая свободного члена c0, все элементы положительны, то
оптимальное решение достигнуто.
2. Если в строке F есть отрицательный коэффициент, а в столбце,
соответствующем ему, нет ни одного положительного элемента, то целевая
функция не ограничена и оптимального решения не существует.
3. Если в столбце над отрицательным коэффициентом целевой функции
есть положительные элементы, то необходимо произвести замену
соответствующей свободной переменной на базисную. В качестве
разрешающего берется тот элемент выбранного столбца, который имеет
одинаковый знак со свободным членом, и для которого симплексное
24
соотношение минимально. С этим разрешающим элементом осуществляется
шаг преобразования таблицы.
4. Операции 1, 2, 3 повторяются до получения оптимального решения.
5.2. ОПРЕДЕЛЕНИЕ ОПОРНОГО РЕШЕНИЯ
До сих пор предполагалось, что свободные и базисные переменные
разделены и все базисные переменные и целевая функция выражены через
свободные, т.е. определено опорное базисное решение. На практике этого нет,
поэтому вначале необходимо найти опорное решение.
В исходной формулировке задачи ЛП могут иметь ограничения в виде
равенств и неравенств.
Чтобы привести к основной задаче ЛП (получить равенства), в
неравенства вводят вспомогательные (дополнительные) переменные, например
yi 0.
n
Так, вместо неравенств aij x j bi , i (l 1)...m , где l - число равенств в
j 1
n
системе ограничений, будут yi bi aij x j , где верхние знаки соответствуют
j 1
приведенному направлению неравенства, а нижние – обратному.
Для применения симплекс-таблиц равенства и неравенства удобно
записать в стандартной форме:
n
y i 0 bi a ij ( x j ), i 1, L ( для равенств ),
j 1
n
y i bi a ij ( x j ), i ( 1 L ), m ( для неравенств ),
j 1
n
целевая функция F c0 c j ( x j ) max .
j 1
Теперь их можно записать в симплексную таблицу:
x1
…
xj
…
x N 1
bi
y1 0
a11
…
a1 j
…
a1( N 1)
b1
…
…
… …
… …
…
yL
a L1
…
a Lj
…
a L ( N 1)
bL
y L1
a( L 1)1
…
a( L 1) j
…
a( L 1)( N 1)
bL1
…
…
… …
… …
…
y M 1
a( M 1)1
…
a( M 1) j
…
a( M 1)( N 1)
bM 1
F
c1
…
cj
…
c N 1
c0
25
В верхнюю часть таблицы заносятся равенства, а после них неравенства.
В последнюю строку таблицы заносятся коэффициенты максимизируемой
целевой функции со знаками, учитывающими вынос знака «минус» ко всем xj ,
отнесенным в исходной симплекс-таблице к числу свободных.
Для поиска опорного решения осуществляется подготовительный этап,
заключающийся в переводе всех нулей из базисных переменных в свободные.
Для перевода каждого из базисных нулей в свободные проводится
преобразование симплекс-таблицы. Последовательность перевода определяется
порядком следования базисных нулей в симплекс-таблице, при этом в качестве
разрешающего элемента выбирается положительный элемент в строке,
соответствующей базисному нулю, подлежащему переводу в свободный.
После подготовительного этапа переходят к этапу нахождения опорного
решения.
Опорное решение считается найденным, если столбец свободных членов
не содержит отрицательных элементов. Если в столбце свободных членов есть
отрицательные элементы, то в строке, соответствующей отрицательному
элементу, ищется любой отрицательный коэффициент. Этот отрицательный
коэффициент и определяет разрешающий столбец. В разрешающем столбце
находится, по минимуму симплексного отношения, разрешающий элемент.
Производятся пересчет таблицы и обмен местами свободной и базисной
переменных. Преобразование симплекс-таблицы продолжается до тех пор, пока
в столбце свободных членов все элементы не станут положительными.
Отсутствие в строке с отрицательным свободным членом отрицательного
коэффициента означает, что система ограничений задачи несовместна с
условиями неотрицательности переменных и задача не имеет решений.
5.3. ОБЩИЙ АЛГОРИТМ СИМПЛЕКСНОГО МЕТОДА
Приведенные выше этапы решения задач линейного программирования
симплексным методом изложены в последовательности, отличающейся от
реального алгоритма, но удобной с методической точки зрения. Фактически
алгоритм и программа симплексного метода предусматривают другую
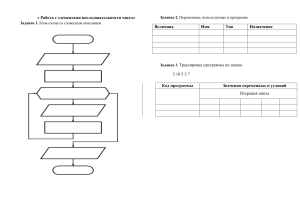
последовательность.
На первом этапе осуществляется перевод базисных нулей в число
свободных и базисные переменные выражаются через свободные переменные.
Это реализуется с помощью преобразования симплекс-таблицы по единому
алгоритму преобразования, включающему поиск разрешающего элемента,
пересчет симплекс-таблицы и обмен в обозначениях базисных и свободных
переменных, как это показано на рисунке.
26
Начало
Ввод исходных
данных
Базисные
переменные
в ыражены через
св ободные?
Нет
Преобразов ание симплекс-таблицы
1. Поиск разрешающего элемент а
2. Пересчёт симплекс-т аблицы
3. Обмен базисной и св ободной переменной
Да
Опорное (базисное)
решение найдено?
Нет
Преобразов ание симплекс-таблицы
(при поиске базов ого решения)
1. Поиск разрешающего элемент а
2. Пересчёт симплекс-т аблицы
3. Обмен базисной и св ободной переменной
Да
Оптимальное
решение найдено?
Да
Вывод значений:
-переменных
-целевой функции
Нет
Преобразов ание симплекс-таблицы
(при поиске опт имального решения)
1. Поиск разрешающего элемент а
2. Пересчёт симплекс-т аблицы
3. Обмен базисной и св ободной переменной
Ограничения
не сов местны
Оптимального
решения не
сущест в ует
Конец
На втором этапе ищется опорное (базисное) решение и с помощью
преобразования симплекс-таблицы исключаются отрицательные элементы в
столбце свободных членов, при этом проверяется совместность системы
ограничений.
На третьем этапе производится преобразование симплекс-таблицы для
поиска оптимального решения и это продолжается до тех пор, пока все
коэффициенты в строке целевой функции не станут положительными. В случае
невозможности этого преобразования, т. е. если в столбце над отрицательным
коэффициентом целевой функции нет положительных элементов, то выдается
сообщение о том, что оптимального решения в данной задаче не существует.
27
6. ИССЛЕДОВАНИЕ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
6.1. ДВОЙСТВЕННОСТЬ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задачи ЛП обладают очень важным свойством двойственности, которое
заключается в следующем.
Если существует исходная задача нахождения максимума целевой
функции F, то существует и двойственная к ней задача нахождения минимума
функционала Ф:
Ф В Т Y min ,
F CX max
(6.1)
AT Y C T ,
AX B
T
Y 0, Y y1* , ... , y i* , ... , y n* ,
X 0
где yi – переменные двойственной задачи.
Существует правило перехода к двойственной задаче, заключающееся в
следующем:
1. j-й столбец, составленный из коэффициентов ограничения исходной задачи,
совпадает с j-й строкой, составленной из коэффициентов ограничений
двойственной задачи.
2. Строка, составленная из коэффициентов целевой функции, совпадает со
столбцом, составленным из констант правых частей ограничений
двойственной модели.
3. Столбец, составленный из констант правых частей ограничений исходной
модели, совпадает со строкой, составленной из коэффициентов целевой
функции двойственной задачи.
4. Направление знаков неравенства в исходной модели противоположно
направлению знаков неравенства в двойственной задаче.
5. Требование максимизации (или минимизации) в исходной задаче заменено
требованием минимизации (или максимизации) в двойственной задаче.
Двойственная задача, сформулированная из чисто математических
соображений, оказывается, тесно связана с прямой (исходной) задачей ЛП. В
частности, равенствам прямой задачи соответствуют переменные двойственной
задачи, неограниченные в знаке, и, наоборот, с равенствами двойственной
задачи соотносятся переменные прямой задачи, неограниченные в знаке:
N 1
N 1
F c j x j max
Ф bi y i* min
N 1
M 1
j 1
aij x j bi , i 1, L
j 1
j 1
a ij y i* c j , j 1, H
j 1
N 1
M 1
j 1
j 1
aij x j bi , i L 1, M 1
a ij y i* c j , j H 1, N 1
x j 0 , j H 1, N 1
y i* 0 , i ( L 1 ),( M 1 )
x j неограниченно во времени , j 1, H
y i* неограниченно в знаке , i 1, L
(6.2)
28
Пример.
F=4x1+5x2+9x3max,
Ф=16y1+25y2min,
x1+x2+2x3=16,
1y1+7y24,
7x1+5x2+3x325,
1y1+5y25,
x10, x20,
2y1+3y2=9,
x3 неограниченно в знаке
y20, y1 неограниченно в знаке
(6.3)
Понятие двойственности имеет большое значение в исследовании операций
благодаря свойствам, сформулированным в теореме двойственности, которая
утверждает:
А. Если исходная и двойственная ей задачи имеют допустимые решения,
то:
1) существует оптимальное решение x *j ( j 1, n) исходной задачи;
2) существует оптимальное решение двойственной задачи y i* (i 1, m) ;
3) при оптимальных значениях переменных максимум целевой функции
одной задачи равен минимуму целевой функции двойственной задачи:
n
m
j 1
i 1
c j x *j bi yi*
или (CX * ) max ( B T Y * ) min .
(6.4)
В. Если исходная задача допускает оптимальное решение, для которого
значение целевой функции ограничено, то соответствующая двойственная
задача допускает оптимальное решение при том же значении целевой функции.
Иначе говоря, если существует оптимальное решение одной задачи, то
должно существовать оптимальное решение и двойственной ей задачи.
Не приводя математического доказательства всех утверждений,
составляющих в совокупности теорему двойственности, имеет смысл
остановиться на некоторых следствиях этой теоремы.
Следствие 1. Можно показать, что любое допустимое решение исходной
задачи линейного программирования накладывает ограничение на оптимальное
значение целевой функции соответствующей двойственной задачи.
Пусть xj и yi удовлетворяют ограничениям, каждая в своей задаче.
Умножим каждое i-е уравнение исходной задачи на yi, а каждое j-е ограничение
двойственной задачи на xj. Т.к. yi 0 и x j0, то направление неравенств не
изменится:
n
y i ( aij x j ) bi yi .
j 1
Теперь сложим почленно левые и правые части по i 1, m :
m
n
m
i 1
j 1
i 1
yi ( aij x j ) bi yi, .
(6.5)
29
Аналогично для двойственной задачи.
m
x j ( a ij y i ) c j x j ,
j 1, n,
i 1
n
m
n
j 1
i 1
j 1
(6.6)
x j ( aij y i ) c j x j .
Правые части находятся в соотношениях:
n
m
c x b y или F Ф.
j 1
j
j
i 1
i
(6.7)
i
Следовательно, из соотношения (6.7) видно, что значение целевой
функции, соответствующее некоторому допустимому (включая оптимальное)
решению исходной задачи, зависит и ограничивается значением целевой
функции для любого допустимого решения (включая оптимальное)
соответствующей двойственной задачи.
Например, для записанных ранее исходной и двойственной задач (6.3)
следует, что допустимыми решениями их могут быть x1=x2=0, x3=8 и y1=0,
y2=3, поэтому целевые функции будут находиться в соотношениях
4x1 + 5x2 + 9x3 16y1 +25y2.
Подставив допустимые решения, получим F=72, Ф=75.
В соответствии со следствием 1 можно утверждать, что оптимальное
значение целевой функции, как для исходной, так и для двойственной задачи,
лежит в интервале от 72 до 75.
Из теоремы двойственности можно вывести следствие 2.
Для допустимых решений прямой и двойственной задач можно записать
ограничения-неравенства
n
aij x j bi 0
j 1
(6.8)
и
m
a y c 0 .
i 1
ij
i
j
(6.9)
Если умножить (6.8) на yi* , а (6.9) на x *j , при этом оба эти неравенства
должны соблюдаться, то для оптимальных значений они превращаются в
равенства
n
m
yi* aij x *j bi 0, i 1, m ; x *j aij yi* c j 0, j 1, n ,
i 1
j 1
откуда следует, что если aij x *j bi 0 (т.е. 0), тогда y i* 0 ;
(6.10)
если aij yi* c j 0 (т.е. 0), тогда x*j 0 .
Таким образом, следствие 2 утверждает, что если одна из задач содержит
ограничение, имеющее вид строгого неравенства (>,<), то соответствующая
переменная в двойственной задаче принимает нулевое значение.
30
6.2. РЕШЕНИЕ ДВОЙСТВЕННОЙ ЗАДАЧИ
Решение двойственной задачи можно найти из конечной (оптимальной)
симплекс-таблицы прямой задачи линейного программирования.
Если исходную прямую задачу линейного программирования представить
в виде F=CX, AXB, где [A]=[aij] – матрица коэффициентов системы, тогда в
исходной симплекс-таблице она имеет вид
y1
x1 b1
y A x b ,
j
i
i
y M 1
x N 1 bM 1
(6.11)
и строка целевой функции будет
x1
Fmax c1 ... c j ... c N 1 x j c0 .
x N 1
(6.12)
Для двойственной задачи Фmin=BTY, ATYCT, Y0
x1*
y1* c1
*
T
*
x j A y i c j ,
x *N 1
y M* 1 c N 1
(6.13)
y1*
Фmin b1 ...bi ...bM 1 y i* c 0 .
y M* 1
(6.14)
Дополнительные переменные yi для ограничений прямой задачи
формально играют роль переменных с обратным знаком двойственной задачи
yi * .
Дополнительные переменные двойственной задачи
могут
x *j
рассматриваться как переменные с обратным знаком прямой задачи xj.
Решение прямой задачи для любой S-итерации может быть записано с
помощью матрицы перехода [Ps] в виде
вектор столбец
базовых переменных P
S
S итерации
b1
b
i
bM 1
вектор столбец
свободных членов
S итерации
вектор -столбец
свобод. членов
исход. симпл.- табл.
Матрица перехода для исходной симплекс-таблицы [P0] (т.е. нулевой
итерации) является единичной диагональной матрицей размерностью
(M-1)(M-1) для прямой задачи и (N-1)(N-1) для двойственной задачи:
1 0 0
P0 0 1 0`
0 0 1
31
Столбцы
матрицы
соответствуют
дополнительным
элементам
*
yi (i 1, M 1) прямой задачи или x j ( j 1, N 1) для двойственной задачи и
располагаются в прямом порядке y1,y2,…,yi,…,yM-1 или x1* , x2* ,..., x *j ,..., x *N 1 .
Если дополнительные переменные yi или x *j прямой и двойственной задач
на данной S-итерации являются базисными, то соответствующие им столбцы
матрицы PS состоят из нулей во всех строчках за исключением одной, в которой
присутствует единица. Номера этих строк совпадают с номерами строк, в
которых находится эта переменная в столбце базисных переменных. Столбцы
матрицы перехода PS для дополнительных переменных yi ( x *j ), которые для
рассматриваемой итерации оказались в числе свободных, соответствуют
коэффициентам симплекс-таблицы на этой итерации.
Так, матрица перехода для S-итерации будет
y1
x1 a11
y 2 a12
PS
x3 a13
x k a k1
x2
y3
0 a13
1 a 23
0 a33
0 ak 3
yk
a1k
a2k
a3k
a kk
.
Обозначим [P] – матрицу перехода конечной симплекс-таблицы, тогда
можно записать в матричном виде решение прямой задачи следующим
образом:
столбец базисных
b1 столбец свободных
переменных конечной P b членов конечной
.
i
симплекс таблицы
bM 1 симплекс таблицы
Аналогично последняя симплекс-таблица двойственной задачи может
быть представлена в виде
столбец базисных
c1 столбец свободных
переменных конечной P * c членов конечной
.
j
симплекс таблицы
c N 1 симплекс таблицы
Из (6.11) и (6.13) следует, что матрица системы двойственной задачи
эквивалентна транспонированной матрице прямой задачи, взятой с обратным
знаком, что справедливо и для матрицы конечной симплекс-таблицы.
Это можно проиллюстрировать на конкретном примере. Допустим,
организуется производство трех видов изделий A, B, C в количестве x1, x2, x3
соответственно из имеющихся запасов сырья b1, b2, b3. При этом на
производство единицы j-го изделия затрачивается aij единиц i-го вида сырья.
Требуется максимизировать доход, если цены на единицу каждого изделия
составляют соответственно с1, с2, с3.
Таким образом, для определения оптимального плана производства
нужно решить задачу, состоящую в максимизации целевой функции:
Fmax 10 x1 14 x2 12 x3 ,
c1
c2
c3
32
при следующих ограничениях:
y1
y2
y3
4x1+2x2+x3180,
b1=180,
3x1+x2+3x3210,
b2=210,
x1+2x2+5x3244,
b3=244,
(6.15)
x1, x2, x3 0.
Конечная симплекс-таблица имеет вид
-x1
-y1
-y3
bi
x2
19/8
5/8
-1/8
82
y2
23/8
1/8
-5/8
80
x3
-3/4
-1/4
-1/4
16
F
57/4
23/4
5/4
1340
При этом матрица перехода конечной симплекс-таблицы прямой задачи
будет
5
0 1
8
8
5
1
P 8 1
.
8
1
4 0 1 4
Как видно из симплекс-таблицы, решение прямой задачи равно x1=0,
x2=82, x3=16, , Fmax=1340.
Кроме того, полезно запомнить значения вспомогательных переменных
y1=y2=0, y2=80.
Двойственная задача запишется следующим образом: найти минимум
функции
Фmin 180 y1* 210 y 2* 244 y3*
b1
b2
b3
при ограничениях:
x1*
4 y1* 3 y 2* y 3* 10,
x 2*
2 y1* y 2* 2 y 3* 14,
x 3*
y1* 3 y 2* 5 y 3* 12,
с1 = 10,
с2 = 14,
с3 = 12.
(6.16)
y1* , y 2* , y 3* 0.
Конечную симплекс-таблицу двойственной задачи исходя из конечной
симплекс-таблицы прямой задачи можно записать в виде
33
x 2*
y 2*
x 3*
cj
x1*
-19/8
-23/8
3/4
57/4
y1*
-5/8
-1/8
1/4
23/4
y 3*
1/8
5/8
-1/4
5/4
Ф
82
80
16
-1340
А матрица перехода для двойственной задачи будет
1 19
8
*
5
P 0
8
1
0
8
3
4
1
4
1
4
Решение двойственной задачи составляет: y1* 23 4 , y 2* 0 , y3* 5 4 ,
Ф= –1340.
При этом полезно знать значения вспомогательных переменных
x1* 57 , x2* x3* 0 для последующего исследования решения задачи.
4
6.3. ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ДВОЙСТВЕННОСТИ
Экономический смысл решения двойственной задачи целесообразно
рассмотреть на конкретном примере (6.15) и (6.16).
Значения переменных y i* двойственной задачи (6.16) можно
рассматривать как ценность (оценку) единичного ресурса i –го вида в прямой
задаче (6.15).
Полученные
значения
переменных
в
двойственной
задаче
*
*
y1 23 / 4 и y 3 5 / 4 показывают, на сколько изменится целевая функция прямой
задачи при изменении на единицу соответственно первого и третьего видов
сырья. При этом значения соответствующих базисных переменных будут
изменяться: для y1 x2 на 5/8, y2 на 1/8, х3 на 1/4; для y3 х2 на 1/8, y2 на 5/8, х3 на
1/4. Значение y 2* =0 означает, что изменение данного вида ресурса не приводит к
изменению целевой функции и этот ресурс использован не полностью для
получения оптимального решения, т.е. имеется скрытый запас ресурса.
Величина этого запаса определяется значением дополнительной переменной
y2=80 в оптимальном решении прямой задачи.
Таким образом, положительную, отличную от нуля двойственную оценку
имеют лишь те виды ресурсов, которые полностью используются при
оптимальном плане производства. Поэтому двойственные оценки определяют
дефицитность используемых ресурсов.
Левые части ограничений двойственной задачи определяют оценку сырья
или ресурса, затраченного на производство единицы каждого вида продукции.
34
Эта оценка должна быть не меньше цены единицы продукции
соответствующего вида.
Если подставить оптимальные значения y1* , y 3* , y 3* двойственной задачи в
ограничения двойственной задачи, то получится: 423/4+0+5/4>10,
223/4+0+25/4=14,
23/4+0+55/4=12.
Первое ограничение выполняется как строгое неравенство. Это означает,
что цена продукта А оказалась ниже, чем двойственная оценка сырья,
затраченного на ее производство, т.е. эта продукция нерентабельна для данного
производства, и, как следует из решения прямой задачи, выпуск продукции А
не предусматривается оптимальным планом производства (х1=0).
Величина превышения затрат над стоимостью определяется значением
*
x1 57 / 4 в оптимальном решении двойственной задачи. Второе и третье
ограничения выполняются как строгие равенства. Это означает, что
двойственная оценка сырья, используемого на производство единиц продукции
В и С, соответствует в точности их ценам. Отсюда следует, что выпуск этих
видов продукции экономически целесообразен и их производство
предусматривается оптимальным планом прямой задачи (х2=82, х3=16).
Целевая функция двойственной задачи показывает общую оценку
(стоимость) сырья, используемого на производство продукции, и она должна
быть минимальной.
6.4. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ РЕШЕНИЯ К ИЗМЕНЕНИЮ ПРАВЫХ ЧАСТЕЙ
ОГРАНИЧЕНИЙ
Рассматривается анализ чувствительности решения к изменению
коэффициентов cj и bi (3.15), (3.16). Для исследования задач линейного
программирования на чувствительность решения к изменению исходных
параметров задачи используется понятие вектора устойчивости решения.
Решение задачи можно записать через матрицу перехода конечной
симплекс-таблицы
b1
X B P bi B ,
bm 1
(6.17)
где [XB] – матрица-столбец базисных переменных конечной симплекс-таблицы;
[P] – матрица перехода конечной симплекс-таблицы прямой задачи;
[b1,…,bi,…,bm-1]T – матрица-столбец свободных членов исходной симплекстаблицы;
[B] – матрица-столбец свободных членов конечной симплекс-таблицы.
Если для исследования на чувствительность коэффициентов bi дать
каждому из них в исходной симплекс-таблице некоторое приращение bi, то
результат решения получит некоторое приращение:
35
b1 b1
X B P bi bi B .
bM 1 bM 1
(6.18)
[B] является вектором устойчивости опорного или оптимального решения
к изменению коэффициентов bi.
Тогда [B] можно определить как
b1
b1
b1
B P bi P bi P bi B.
bM 1
bM 1
bM 1
(6.19)
Исходя из условия неотрицательности значений переменных [XB] и,
следовательно, неотрицательности [XB]= [B]0 можно найти пределы
изменения каждого коэффициента bi.
Анализ чувствительности полученного решения прямой задачи к
изменению правых частей ограничений, т.е. bi, предполагает, что вычисляются
пределы изменения каждого из коэффициентов, при которых оптимальное
решение прямой задачи существует (или оптимальные значения переменных
двойственной задачи y i* const ).
Вектор устойчивости решения прямой задачи к коэффициентам bi
запишется:
p11 (b1 b1 ) ... p i1 (bi bi ) ... p ( M 1)1 (bM 1 bM 1 )
b1 b1
B P bi bi
p1 j (b1 b1 ) ... p ij (bi bi ) ... p ( M 1) j (bM 1 bM 1 )
.
bM 1 bM 1 p1( M 1) (b1 b1 ) ... p i ( M 1) (bi bi ) ... p ( M 1)( M 1) (bM 1 bM 1 )
Условия неотрицательности компонент вектора [B] приводят к системе
неравенств:
p11 (b1 b1 ) ... pi1 (bi bi ) ... p( M 1)1 (bM 1 bM 1 ) 0
p1 j (b1 b1 ) ... pij (bi bi ) ... p( M 1) j (bM 1 bM 1 ) 0
, i 1, M 1
p
1( M 1) (b1 b1 ) ... pi ( M 1) (bi bi ) ... p( M 1)( M 1) (bM 1 bM 1 ) 0
или после приведения подобных членов:
B11p b1 ... Bi1p bi ... BpM 11 bM 1 0
B1pj b1 ... Bijp bi ... B(pM 1) j bM 1 0
.
(6.20)
B p b ... B p b ... B p
i ( M 1)
i
( M 1)( M 1) bM 1 0
1( M 1) 1
Анализ изменений всех коэффициентов одновременно затруднителен и
требует решения сложных систем неравенств.
На практике предполагается изменение только одного коэффициента,
например b1, и тогда b10, а остальные bi=0, i 2, M 1 , при таких условиях
решается рассмотренная выше система неравенств для определения
допустимых пределов изменения b1. Аналогично исследуются пределы
изменения остальных коэффициентов bi. Для определения пределов изменения
целевой функции F прямой задачи, при соответствующих приращениях bi,
36
используется полученное значение переменных двойственной задачи y i* . Ранее
установили, что каждому i-му ограничению прямой задачи соответствует
переменная двойственной задачи. Если двойственная переменная y i* в
последней симплекс-таблице двойственной задачи находится в числе
свободных и, следовательно, y *j 0 , то приращение целевой функции
определяется как F yi* bi 0 .
Если y i* находится в числе базисных переменных последней симплекстаблицы и вычислены допустимые пределы изменения коэффициента bi, т.е.
biminbibimax,
то пределы изменения целевой функции будут bi min yi* F bi max yi* .
6.5. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ РЕШЕНИЯ К ИЗМЕНЕНИЮ КОЭФФИЦИЕНТОВ
ЦЕЛЕВОЙ ФУНКЦИИ
Анализ чувствительности к изменению коэффициентов целевой функции
cj предполагает определение пределов изменения этих коэффициентов при
условии неизменности полученного оптимального решения.
При исследовании на чувствительность решения к изменению
коэффициентов целевой функции cj прямой задачи удобно воспользоваться
решением двойственной задачи. Для двойственной задачи конечная симплекс c1
таблица в матричном виде может быть записана: YB P c j C ,
c N 1
*
(6.21)
где [YB] – матрица-столбец базисных переменных конечной симплекс-таблицы
двойственной задачи;
[P*] – матрица перехода базисных переменных конечной симплекстаблицы двойственной задачи;
c1
c
j
c N 1
- матрица-столбец исходных коэффициентов целевой функции
прямой задачи (в двойственной задаче они играют роль правых частей
ограничений);
[C] - матрица-столбец конечных значений коэффициентов cj двойственной
задачи (для прямой задачи это конечное значение коэффициентов целевой
функции).
Аналогично рассмотренному ранее вводится понятие вектора
устойчивости оптимального решения двойственной задачи к коэффициентам
cj:
C P *
c1 c1
c c P *
j
j
c N 1 c N 1
c1
c P *
j
c N 1
c1
c P*
j
c N 1
c1
c C . (6.22)
j
c N 1
37
Для исследования на чувствительность решения к изменению
коэффициентов cj исходят из следующих соображений: значения приращений
cj
как компонент вектора устойчивости [C] должны иметь знак,
соответствующий оптимальным коэффициентам в строке целевой функции
последней симплекс-таблицы (иначе решение станет уже не оптимальным).
Вектор устойчивости коэффициентов cj может быть записан через
матрицу преобразования двойственной задачи [P*] в виде
c1 c1
C P * c j c j .
c N 1 c N 1
(6.23)
Условие неотрицательности для компонент вектора-столбца [C],
аналогично рассмотренному [B], может быть представлено в виде системы:
c11p c1 ... c1pj c j ... c1p N 1 c N 1 0
cip1 c1 ... cijp c j ... cip( N 1) c N 1 0
c p c ... c p c ... c p
( N 1) j
j
( N 1)( N 1) c N 1 0.
( N 1)1 1
(6.24)
Анализ этой системы легко осуществить отдельно для изменения каждого
коэффициента cj . Пределы изменения коэффициента cj при переменной xj,
оказавшейся в последней симплекс-таблице прямой задачи в числе свободных,
определяются непосредственно коэффициентом в строке целевой функции этой
переменной (например, с157/4 из симплекс-таблицы прямой задачи означает,
что изменение с1 на величину с157/4 не приводит к изменению как
оптимального решения, так и целевой функции).
Изменение коэффициентов при переменных, оказавшихся в числе
базисных последней симплекс-таблицы, приводит к изменению целевой
функции.
Например, с2 и с3 при х2 и х3 , приращения с2 и с3 приведут к
изменению целевой функции на величину F = с2x2+с3x3. При сохранении
неизменным полученного оптимального решения х2=const, x3=const.
При одновременном изменении нескольких коэффициентов решается
система неравенств.
7. РЕШЕНИЕ ТРАНСПОРТНЫХ И СЕТЕВЫХ ЗАДАЧ
7.1. ТРАНСПОРТНАЯ ЗАДАЧА ОТКРЫТОГО ТИПА
В общем виде транспортная задача формулируется в следующем виде.
Заданы m пунктов отправления с запасами грузов a1 ,..., ai ,..., am , n пунктов
потребления подали заявки на груз в количестве b1 ,..., b j ,..., bn , известна
стоимость перевозки единицы груза с ij из i-го пункта отправления в j-й пункт
назначения. Вводятся переменные, определяющие количество отправляемых
грузов из i-го склада в j-й пункт потребления, – xij.
38
Ставится задача минимизировать стоимость перевозок, поэтому целевая
функция будет
n
n
F cij xij min .
(7.1)
i 1 j 1
Количество груза, отправляемого с каждого склада, не должно превышать
имеющихся запасов:
m
x a , i 1, m .
i 1
ij
(7.2)
i
Условие выполнения заявок каждого пункта потребления запишется в
виде
n
x b , j 1, n .
j 1
ij
(7.3)
j
При равенстве количества запасов и заявок пунктов потребления, т.е.
m
n
i 1
j 1
ai b j ,
(7.4)
задача называется сбалансированной. В случае если заявок больше или меньше
запасов, транспортная задача называется открытой (несбалансированной).
Решение таких задач возможно путем введения дополнительных условий.
Рассматриваются два случая.
m
n
i 1
j 1
1. Если запасы больше потребностей: ai b j , то для сведения этой
задачи к сбалансированной задаче вводится фиктивный пункт назначения bn 1 с
потребностями
m
n
i 1
j 1
bn1 ai b j
(7.5)
и допущением, что стоимость перевозки единицы груза между любым пунктом
i и фиктивным пунктом bn 1 равна нулю, т.е. ci(n+1) = 0, i=1, m .
Очевидно, что оптимальное решение такой задачи будет оптимальным и
для исходной.
m
n
i 1
j 1
2. Когда запасы меньше потребностей ai b j , удовлетворение всех
пунктов в этом случае невозможно, поэтому необходимо управлять
транспортировкой таким образом, чтобы наиболее важные пункты
удовлетворялись полнее и чтобы стоимость перевозок была бы минимальной.
Обозначим: rj – величина ущерба на одну единицу груза в результате
невыполнения запроса j-го пункта. Тогда для приведения этой задачи к
основной вводится фиктивный пункт отправления Аm+1 с запасами
n
m
j 1
i 1
a m1 b j ai
(7.6)
и предполагается, что стоимость перевозки единицы груза между этим пунктом
и любым пунктом назначения равна нулю, т.е. c(m+1)j = 0 для всех j=1, n .
Далее минимизируем затраты
39
m
n
n
i 1 j 1
j 1
F cij xij r j y j min ,
(7.7)
где yj – количество груза, «недовезенного» в пункт j при тех же ограничениях и
дополнительном условии
m
y j b j xij , j 1, n .
(7.8)
i 1
7.2. ОПРЕДЕЛЕНИЕ ДОПУСТИМОГО БАЗИСНОГО РЕШЕНИЯ ТРАНСПОРТНОЙ
ЗАДАЧИ
При решении транспортных задач используют не симплексную таблицу, а
матрицу перевозок, в которой совмещены матрица решений и матрица
стоимости перевозок:
X
x11 x12 x1n
x m1 x m 2 x mn
,
C
c11 c12 c1n
c m1 c m 2 c mn
.
Таким образом, каждой клетке такой матрицы соответствуют два числа
xij, cij, как показано в таблице 7.1.
Таблица 7.1
A1, …,Ai, …,Am – обозначения
Ai/Bj B1 …
Bj
… Bn
пунктов отправления, B1,…,Bj,…,Bn –
A1
c11
…
c1n
a1
обозначения пунктов назначения.
x11
x1n
В матрице перевозок приведены
Ai
…
cij
…
ai
также запасы пунктов отправления и
xij
потребности
(заявки)
пунктов
Am
cm1
…
cmn
am
назначения.
xm1
xmn
В матрице перевозок существуют
b1
bj
bn
базисные (занятые) и свободные
(незанятые) клетки. Базисные клетки
соответствуют базисным переменным, и в них записываются значения
базисных неизвестных из допустимого базисного решения (в том числе и
нулевые). Свободные клетки, соответствующие свободным переменным, не
заполняются, нули в них не записываются. Число базисных переменных в
матрице перевозок: r=m+n-1.
Существует несколько методов нахождения допустимого базисного
решения.
Первым рассматривается диагональный метод (метод северо-западного
угла) на конкретном примере с цифровыми данными, приведенными в таблице
7.2.
40
Таблица 7.2
В1
В2
А1 2
3
х11=20
А2 3
2
При этом методе, начиная с
угловых объектов, попытаемся
30
2
4
удовлетворить
потребность
пункта В1 запасами пункта А1.
40
5
1
Это можно сделать, т.к. a1>b1.
Удовлетворим его, осуществив
А3 4
20
3
2
6
перевозки
х11=20. Пункт В1
удовлетворенным
20
30
30
10
=90 оказывается
полностью, поэтому этот столбец
можно временно исключить, в результате получаем таблицу 7.3.
Таблица 7.3
Запасы пункта А1 при этом
В2
В3
В4
ai
уменьшаются и становятся равными
a1
a1=30-20=10.
Далее
попытаемся
A1 x12=10
30-20=10
удовлетворить потребность пункта В2
A2
40
(играющего теперь роль первого)
запасами пункта А1. Т.к. b2 > a1, то
A3
20
потребности можно удовлетворить
bj
b2=30 30
10
70
лишь частично x12=10 единицами груза
из А1. При этом потребности b2 сократятся и станут равными b2=b2 – a1=30 –
10= 20, при этом запасы пункта А1 окажутся исчерпанными, и его строку
можно исключить, что приводится в таблице 7.4.
Таблица 7.4
В2
В3
x22=10
A2
A3
bj b2’=20 30
В3
В4
10
В4
ai
40
20
60
Для этой таблицы выбирается х22=20, при этом сокращаются запасы А2.
Они становятся равными a2 = a2 – b2 = 20 единицам груза. Столбец В2
исключается, получается новая таблица.
Таблица 7.5
A2
A3
bj
В3
В4
ai
x23=20
а2’=20
x33=10 x34=10 20
30
10
40
В таблице 7.5 перевозится в текущем северо-западном углу x23=20, т. к.
запасы А2 составляют только а2’=20. Исключается строка А2, а оставшиеся
потребности b3’=b3 – a2 ’= 10 удовлетворяются перевозками x33=10 и x34=10.
Следует заметить, что при каждом шаге удовлетворяется и вычеркивается
только один пункт – либо отправления, либо назначения. И только на
последнем шаге удовлетворяются одновременно два пункта.
41
Таким образом, получим для решения задач возможные допустимые
значения базисных переменных х11=20, х12=10, х22=20, х33=10, х23=20, х34=10.
Общая стоимость перевозок F=290. Это и есть допустимое базисное решение,
приведенное в таблице 7.6.
Таблица 7.6
В1
В2
В3
В4
А1 2
30
3
2
4
х11=20
х12=10
А2 3
40
2
5
1
х22=20
х23=20
А3 4
20
3
2
6
х33=10
х34=10
20
30
30
10
=90
Число базисных переменных равно r=m+n-1=6, т.е. соответствует
требуемому числу базисных переменных.
Второй метод нахождения исходных базисных решений транспортной
задачи - это метод наименьшей стоимости.
В этом методе выбор пунктов перевозки осуществляется с учетом
стоимости, и на каждом шаге пытаются добиться меньшей стоимости
перевозок.
A1
В1
В2
В3
В4
2
3
2
4
ai
30
1
40
20
A2
3
10
2
5
30
A3
4
3
0
bj
20
2
30
3
x24=10
2
4
6
20
10
=90
20
30
1
Из таблицы следует, что минимальная стоимость перевозок будет между
пунктами А2 и В4, поэтому полагаем х24=10. Удовлетворяем пункт В4 и
мысленно исключаем этот столбец. Запасы а2 уменьшились и стали a2 = a2 – b4
= 30. Следующая по цене стоимость «2» перевозок в нескольких клетках.
Выбираем пункты А1 и В1, полагаем х11=20, тогда a1 = a1 – b1 = 10.
Удовлетворяем В1 и исключаем его (мысленно) из рассмотрения. Затем
выбираем клетку 2-2, полагаем х22=30 и исключаем строку А2, т.к. запасы
исчерпаны (но В2 не исключаем, т.к. два исключения одновременно
запрещаются), поэтому удовлетворим В2, но его «нулевая» потребность
осталась.
Следующей клеткой (по-прежнему с ценой «2») выбираем 1-3, т.к. b3>a1,
то возьмем x13 = a1’ = 10, исключаем строку А1. Потребность пункта В3
42
уменьшилась до b3’ = b3 – a1’=20. Теперь в матрице перевозок осталось два
пункта В2 с нулевой потребностью b2 =0 и В3 с потребностью b3’ = 20.
Удовлетворяем потребности В2 и В3, полагая х32=х33=20. F =170. Таким
образом, получили допустимое базисное решение методом наименьшей
стоимости.
7.3. РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ
Распределительный метод использует исходное базисное решение,
полученное методом северо-западного угла или наименьшей стоимости, и
заключается в преобразовании матрицы перевозок таким образом, что каждый
последующий пересчет таблицы приближается к оптимальному решению.
Для преобразования таблицы используется понятие цикла.
Циклом в матрице называется ломаная с вершинами в клетках и
звеньями, лежащими вдоль строк и столбцов матрицы, удовлетворяющая
требованиям:
– замкнутости;
– в каждой вершине должно встречаться два звена.
Если в любом цикле вершинам приписать при обходе в одном
направлении поочередно знаки «+» и «–», то в каждой строке (столбце) число
положительных вершин будет равно числу отрицательных.
При решении задач используется операция сдвига по циклу. Эта операция
заключается в увеличении элементов в положительных вершинах и
уменьшении в отрицательных на одно и то же число.
Например, для свободной клетки с координатами (3,3) левой матрицы
строится цикл, приведенный на рисунке, и осуществляется сдвиг по циклу на
величину 8. В результате получаются новые значения перевозок, приведенные
на правой матрице. Клетки, не являющиеся вершинами цикла, при этом
остаются без изменений.
—
20
+
10
8
—
8
6
+
18
Сдвиг по
циклу на 8
12
8
0
6
8
Для оптимизации решения важно знать, с каким коэффициентом выбранная
свободная неизвестная входит в выражение для базисных неизвестных. Это
определяется следующим правилом:
– коэффициент равен 0, если соответствующая базисная клетка не является
вершиной цикла пересчета данной свободной клетки;
– коэффициент равен 1, если базисная клетка является положительной
вершиной цикла пересчета данной свободной клетки;
– коэффициент равен –1, если базисная клетка является отрицательной
вершиной пересчета данной свободной клетки.
43
Например, матрица перевозок имеет 4 пункта отправления и 4 пункта
назначения. В ней записано некоторое базисное решение в заштрихованных
клетках x11 , x12 , x23 , x24 , x32 , x41 и x43 , число которых должно быть r=m+n-1=7.
При этом в каждой строке и каждом столбце таблицы должна быть как
минимум одна базисная клетка.
А1
В1
–
В2
В3
В4
+
+
А2
–
А3
А4
–
+
Построим цикл пересчета для свободной
клетки x14 так, чтобы все остальные вершины
лежали в базисных клетках. Такой цикл
существует только один и приведен в таблице, при
этом свободной клетке x14 присваивается знак «+»,
а знаки всех последующих вершин чередуются при
их обходе по циклу в одном направлении.
Таким образом, можно по теореме утверждать, что клетка x14 входит в
выражение для неизвестных базисных со знаками:
x11 x12
1 0
x23
x24
1
1
x32
x41
0
1
x43
.
1
Аналогично можно найти коэффициенты для других свободных
неизвестных.
У распределительного метода существуют промежуточные базисные
решения, каждое из которых постепенно приближается к оптимальному.
Найденное любым методом допустимое базисное решение вносится в
матрицу перевозок и занимает r=m+n-1 клеток. Вносятся и нулевые базисные
решения. Далее меняются местами базисные и свободные переменные для
приближения к оптимальному решению.
Во-первых, определяется свободная неизвестная, переводимая в число
базисных.
Рассмотрим способ определения свободных неизвестных, которые
целесообразно перевести в число базисных на конкретном примере. Возьмем
базисное решение, найденное методом северо-западного угла со стоимостью
перевозок
3
4
F cij xij =220 + 310 + 220 + 520 + 210 + 610 = 290.
i 1 j 1
Теперь необходимо построить циклы пересчета для всех свободных
переменных (свободных клеток) и определить сумму стоимостей по циклам
пересчета ij для всех свободных неизвестных, чтобы найти, какую из них
перевести в число базисных для уменьшения целевой функции.
44
В1
В2
A1
2
3
A2
3
A3
4
bj
20
В3
–
20
2
+
5
–
В4
ai
4
30
1
40
10
2
+
20
3
20
2
6
10
30
30
10
20
10
Определяем сумму стоимостей по циклу пересчета для каждой свободной
клетки, подставляя соответствующие стоимости перевозок из базисных клеток
в вершинах цикла:
х13 13 = с13 - с23 + с22 - с12 = 2 - 5 + 2 - 3 = -4 ,
х14 14 = с14 - с24 +с33 – с23 + с22 - с12 = 4 – 6 + 2 - 5 + 2 - 3 = -6 ,
х21 21 = с21 - с11 + с12 - с22 = 3 - 2+ 3 - 2 = 2 ,
аналогично 24 = - 8, 31 = 6, 32 = 4.
Выбираем те из свободных переменных, которые имеют отрицательное
значение суммы стоимости по циклу пересчета. В рассматриваемом примере
это х13, х14, х24.
Во-вторых, определяется базисная переменная, переводимая в число
свободных.
Для
этого
необходимо
проанализировать
цикл
пересчета,
соответствующий выбранной свободной неизвестной. В нашем примере это
может быть цикл для переменной х13.
Производя преобразования по циклу, мы должны получить нуль в одной
из базисных переменных. Кроме того, необходимо учитывать, что переменные
не могут принимать отрицательных значений. Поэтому выбирается та базисная
переменная, которая имеет наименьшее значение из всех базисных
переменных, расположенных в отрицательных вершинах цикла пересчета. В
нашем примере это будет х12=10.
Для получения нового допустимого базисного решения осуществляем
сдвиг по циклу пересчета выбранной свободной переменной х13 на величину
значений выбранной базисной переменной х12=10, которая после сдвига
переводится в свободные.
При этом получим новую таблицу матрицы перевозок.
В1
В2
В3
В4
ai
A1
2
3
2
4
30
A2
3
1
40
A3
4
bj
20
20
10
2
5
30
3
10
2
6
10
30
30
10
10
20
45
Сдвиг по циклу привел к новому допустимому базисному решению:
х11=20, х13=10, х22=30, х23=10, х33=10, х34=10, остальные xij=0.
Новое решение дает значение целевой функции F=250, меньшее
предыдущего, т. е. ближе к оптимальному значению.
Если в отрицательных вершинах с минимальными перевозками окажется
две базисных клетки с одинаковыми значениями, то после сдвига по циклу в
число свободных переводится только одна из них, а вторая остается в числе
базисных с нулевыми перевозками. И в дальнейших расчетах эта клетка
фигурирует как базисная со всеми их характеристиками.
Для нового базисного решения также подсчитываются суммы стоимостей
по циклам пересчета для каждой свободной неизвестной: 12=4, 14=2, 12=4,
21= - 2,24= - 8, 31= 2, 23= 4.
Выбираются новые свободная и базисная переменные для сдвига по
новым циклам, и все повторяется. Операция продолжается до тех пор, пока не
получится, что все стоимости по циклам пересчета больше нуля (ij > 0), что
является признаком оптимальности решения, полученного распределительным
методом.
Для рассматриваемого примера оптимальным решением является
следующее:
х11=20, х13=10, х22=30, х24=10, х33=10, х12=0, остальные xij=0. Стоимость
оптимальной перевозки F=170, и уменьшить ее дальше невозможно.
7.4. МЕТОД ПОТЕНЦИАЛОВ ДЛЯ РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ
m
n
Формулировка транспортной задачи: F cij xij min ,
i 1 j 1
при ограничениях X mn I m B – удовлетворение запросов пунктов потребления,
X mn I n A – отправка грузов не должна превышать запасов (равна для задачи
закрытого типа).
T
m
xij b j ,
j 1, n,
i 1
n
xij ai , i 1, m,
j 1
x ij 0,
m
n
i 1
j 1
ai b j – сбалансированная транспортировка.
46
В1 …
c11
Вt
Bq …
Bn
ai
Сущность метода состоит в
что
каждому
пункту
a1 том,
сопоставляют некоторые векторы,
As
cs1
csq
называемые потенциалами пункта:
as
xst
xsq
Aii , Bj j. Для определения
Ap
cpt
cpq
ap потенциалов необходимо иметь
xpq
одно из допустимых базисных
Am cm1
cmn
am
решений.
Существуют
b j b1
bt
bq
bn
соотношения, показывающие, что
алгебраическая сумма стоимости по циклу пересчета свободной клетки равна
разности между стоимостью и суммой потенциалов:
(7.9)
ij cij ( i j ) .
A1
Свяжем все пункты, соответствующие базисным переменным,
уравнениями: i +j = cij , где cij –стоимость перевозки единицы груза из i-го
пункта в j-й. Объединение всех уравнений для базисных неизвестных образует
систему с числом уравнений r = m + n – 1 и числом неизвестных потенциалов
(m+n).
Система уравнений для рассматриваемого общего случая при базисных
клетках xsl , xsq , xpq будет
...
c ,
t
st
s
s q c sq ,
...
p q c pq ,
...
(7.10)
Решить систему уравнений нетрудно, т.к. ее ранг равен рангу системы
ограничений задачи, т.е. r = m + n – 1, и за свободную переменную можно взять
любую из неизвестных i, j .
В качестве свободной переменной, например, можно принять S и
придать ей произвольное значение (удобно нуль).
Далее рассматривают все базисные неизвестные xst, которые
располагаются в s-й строке матрицы перевозок. Каждой такой неизвестной
соответствует в системе определенное уравнение s + t = cst.
Т.к. s задаются, то из уравнения можно найти t (например, s=0, t= cst).
Так же находятся все остальные t из s-й строки, например q=сsq. После этого
останавливаются на одном из найденных , например q, и рассматривают все
те базисные неизвестные xpq, которые располагаются в q-м столбце матрицы.
Каждой такой неизвестной отвечает уравнение: p + q = cpq. Но, т.к. q найдено
ранее (q= сsq), то из такого уравнения можно найти p = cpq - q = cpq - сsq. Так
находятся все p, соответствующие всем базисным неизвестным xpq из q-го
столбца.
Этот процесс продолжается, пока не будут найдены все i, j, т.е. пока не
будут определены потенциалы всех пунктов.
47
Алгоритм решения транспортной задачи методом потенциалов
1. Записываются уравнения задачи.
2. Определяется каким-либо способом допустимое базисное решение.
3. С помощью уравнений для базисных клеток находятся потенциалы i и j
всех пунктов отправления и назначения.
4. Определяется сумма стоимости по циклам пересчета ij = cij – (i + j) для
всех свободных переменных. Выбирается свободная переменная xi0j0 , для
которой i0j0 отрицательна и является наибольшей по абсолютной величине.
Если таких нет, то это означает, что данное базисное решение оптимально.
5. Для выбранной переменной xi0j0 строится цикл пересчета и
осуществляется сдвиг на величину наименьшего значения базисной
переменной в отрицательных вершинах.
6. Далее операции 2 – 5 повторяются, пока не будет получено оптимальное
решение, т. е. пока все ij не станут положительными.
7. Вычисляется общая стоимость перевозок, соответствующая оптимальному
решению.
Рассмотрим пример определения потенциалов. Данные задачи и одно из
допустимых базисных решений приведены в таблице.
A1
В1
2
В2
3
20
A2 3
B3
2
B4
4
5
1
10
2
20
A3 4
3
20
2
6
10
bj
10
ai
i
30
0
40
-1
20
-4
Составим систему уравнений
для
определения
потенциалов
пунктов отправления и назначения:
1 1 2 ,
3 ,
2
1
2 2 2 ,
2 3 5 ,
3 3 2 ,
3 4 6 .
20
30
30
10
3
6
10
j 2
Число уравнений равно числу базисных переменных.
Примем в качестве свободной неизвестной 1, положим 1 =0.
В первой строке таблицы имеется две базисные неизвестные x11 , x12 , им
соответствуют уравнения 1 +1 =2 и 1 +2 =3. Из этих уравнений находим
1=2, 2 =3.
В первом столбце таблицы содержится одна базисная неизвестная x11 ,
соответствующее ей уравнение уже было использовано.
Во втором столбце кроме x12 содержится базисная переменная x22. Ей
соответствует уравнение 2 +2 =2. Т. к. 2 =3, значит 2 =2 – 2 = –1.
Во второй строке кроме рассмотренной x22 имеется базисная неизвестная
x23. Из соответствующего ей уравнения 2 +3 =5 при условии 2 = –1 следует,
что 3 =5 – 2 =6.
В третьем столбце кроме базисной x23 есть x33. Из уравнения 3 +3 =2 по
известному значению 3 находим 2 = –4.
48
И, наконец, из уравнения для базисной неизвестной x34 3 +4 =6
определяем 4 =6 – 3 =10.
Теперь можно найти алгебраическую сумму стоимостей по циклу пересчета
свободных переменных. Так, для свободной переменной x13 имеем 13 = с13 –
– (1 +3) =2 – (0+6) = - 4. Аналогично находим
14 = -6 , 21 =2, 24 = - 8, 31 =6, 32 =4.
Далее выбирается свободная неизвестная, для которой ij отрицательна и
имеет наибольшую абсолютную величину (в нашем случае это 24 = - 8, и для
нее будет x24). Для выбранной переменной определяется цикл пересчета и
осуществляется сдвиг по циклу на наименьшее значение базисной неизвестной
в отрицательной вершине.
Далее повторяются предыдущие вычисления вплоть до получения
оптимального значения, когда все ij будут положительны.
7.5. РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ ПО КРИТЕРИЮ ВРЕМЕНИ
В ряде транспортных задач необходимо минимизировать время для
доставки груза. В таких задачах задаются:
ai – запасы груза пункта отправления;
bj – потребности груза в пунктах назначения;
tij – время доставки груза из i-го в j-й пункт.
Допускается, что коммутационные сети обладают неограниченной
пропускной способностью, т.е. tij не зависит от количества перевозимого груза
или передаваемой информации.
Время реализации всего плана перевозок определяется максимальным
значением времени перевозки в наиболее отдаленные пункты, следовательно,
(t ij ) . А
если нашли N допустимых решений, то общее время перевозки T max
N
для нахождения оптимального решения необходимо найти такое допустимое
решение S, время реализации которого минимально.
Для решения этой задачи используется метод разгрузочных цепей.
Алгоритм решения состоит из следующих шагов
1. Вносятся исходные данные ai, bj, tij в матрицу перевозок.
2. Находится любым методом исходное допустимое решение и заносится в
матрицу перевозок. Не пишутся в матрице только нулевые базисные
переменные и свободные переменные.
3. Определяется максимальное время реализации, записанного в матрице
решения задачи, т.е. max t ij t i j .
1 1
4. Исследуется клетка с максимальным временем i1j1 на возможность
разгрузки, т.е. проверяется в матрице решение на оптимальность. Признаком
оптимальности решения транспортной задачи по критерию времени является
невозможность построения разгрузочной цепи для клетки с максимальным
tij.
49
5.
При
наличии
разгрузочной
цепи
исключают
переменную
xi j ,
1 1
находящуюся в клетке с максимальным временем, из данного решения и строят
новое допустимое решение более, близкое к оптимальному.
Разгрузочная цепь является замкнутым циклом, который охватывает как
базисные, так и свободные клетки. При этом в разгрузочную цепь не должны
входить свободные клетке с tij больше максимального t i j . Разгружаемая цепь
1 1
изображается всегда так, что разгружаемой клетки приписывается знак «-» и в
отрицательных вершинах обязательно находятся базисные переменные.
Пример. Исходное допустимое базисное решение, найденное, например,
диагональным методом, приведено в таблице:
В1
В2
В3
В4
А1
20
5
10
20
А2
10
10
5
15
А3
10
5
5
20
А4
5
20
ai
X 25
5
15
15
10
5
15
8
8
10
5
30
35
bj
20
25
20
30
Далее вычеркиваем все свободные клетки с tij t11, чтобы не использовать
их для цикла переноса (это клетка t14).
Пытаемся разгрузить клетку 1,1. Она имеет сейчас несколько разгрузочных
цепей: а) 1,12,12,21,2; б) 1,13,13,21,2;
в) 1,13,13,31,3; г) 1,14,14,31,3.
Однако ни одна из них не позволяет разгрузить клетку за один прием:
вначале разгрузим ее на величину 15 по циклу (а), а затем по циклу (б) на
величину 5.
В результате получим новое решение в таблице:
В1
А1
20
А2
10
А3
А4
bj
В2
5
Х
15
10 –
10
10
Х
8
5
+
15
8
5
25
20
25
15
20
10
– 5
+
20
X
Х
5
ai
20
Х
Х
5
В4
10
25
15
5
В3
30 35
30
50
Для этого решения max(tij)=t21=t31=t44=10. Вычерчиваем все свободные
клетки с tij10, это 1,3; 2,3; 3,2 и, конечно, 1,1 и 2,2.
Попытаемся разгрузить клетки 2,1; 3,1; 4,4. Клетку 3,1 можно разгрузить
по циклу 3,14,14,33,3. Выполним операцию сдвига на х31=5 и получим
решение в следующей таблице:
В1
А1
А2
20
10 _
15
А4
5
+
20
20
10
10
ai
Х
Х
Х
В4
10
25
15
10
В3
5
Х
А3
bj
В2
X
5
+
15
Х
5
Х
5
20
8
8
10
25
20
30
5
25
+
_
30
20
35
Теперь разгрузим клетку 2,1 по циклу 2,14,14,42,4, а затем клетку 4,4
по циклу 4,44,33,33,4. В результате получим решение, данное в таблице:
В1
А1
20
А2
10
А3
10
А4
5
bj
20
В2
В3
5
Х
10
15
10
Х
10
Х
25
15
5
5
8
Х
20
5
5
8
X
Х
Х
15
10
Х
15
20
ai
20
Х
25
Х
В4
25
15
20
35
30
Для реализации этого решения требуется max(tij)=t43=8.
Вычеркнем из таблицы свободные клетки с t8, (т.е. клетку 4,2).
Попытаемся разгрузить клетку 4,3. Сделать этого нельзя, т.к. в 4-й строке и в 3м столбце нет незачеркнутых свободных клеток. Следовательно, решение,
записанное в таблице, является оптимальным по критерию времени и найти
план, который можно реализовать за время меньше tij=8, невозможно.
7.6. РЕШЕНИЕ СЕТЕВЫХ ЗАДАЧ МЕТОДОМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Сетевые задачи относятся к группе транспортных с единственным
отличием, заключающимся в том, что перевозка груза (или в данном случае
удобней рассмотреть - информации) осуществляется через промежуточные
пункты. Ставится задача организации оптимальных путей передачи
информации по существующей сети связи. В качестве критериев
оптимальности могут анализироваться такие как минимизация длины,
стоимости искажений или максимизация надежности, достоверности и т.д.
51
Применительно к перевозкам грузов это также может быть минимизация
расхода горючего, стоимости и др.
Модель сети связи, используемая для передачи информации, можно
рассматривать как совокупность ветвей и узлов и представить в виде графа,
вершины которого поставлены в соответствие узлам, а ребра – ветвям, как
показано на рис.7.1 для примера с 5 пунктами передачи и ретрансляции.
Граф может быть неориентированным,
15(4)
если связь по всем ветвям двухсторонняя,
1 15(3)
или ориентированным, если имеют место
односторонние (т.е. в одном направлении)
5
2
15(9)
связи между отдельными узлами,
15(2)
10(6) 20(8)
например 12 на рис.7.1.
В общем случае некоторые характеристики ветвей могут не совпадать по раз4
3
10(8) 10(7)
ным направлениям, например стоимость
передачи единицы информации в одном
Рис. 7.1
направлении будет отличаться от стоимости в обратном направлении.
Каждая ветвь характеризуется двумя параметрами. Один параметр – это
емкость или пропускная способность ij, которая ограничивает возможности
передачи определенного объема информации между пунктами i и j. На рис.7.1,
например, пропускная способность односторонней ветви 12 = 15, а
двухсторонних, совпадающая в обоих направлениях, - 15 = 51 = 15, 34 = 43 =
10, 23 = 23 = 20 и т.д.
Второй параметр каждой ветви зависит от выбранного критерия
оптимизации. Это может быть и длина ветви lij, и стоимость передачи единицы
информации cij по данной ветви, и другие параметры. Как отмечено выше, для
двухсторонних ветвей эти параметры могут не совпадать, например на рис.7.1.
Стоимость, указанная в скобках, для ветви с43 = 8, а с34 = 7.
Для полной характеристики сети используются матрица пропускных
способностей (емкостей) В и, например, матрица стоимостей С,
соответствующие приведенной на рис.7.1 сети связи
0
B0
0
15
15
0
0
20
10
20
10
10
10
0
15
15
15
0
15,
15
0
C 0
0
4
3
0
0
5
6
5
7
6
8
0
9
2
4
0
9 .
2
Для передачи заданных потоков информации между парами узлов
образуются пути, которые включают последовательности узлов и ветвей и при
этом
52
ни один из узлов не встречается дважды. Так, если требования на потоки
информации Ф задать в матричном виде
0
0
Ф 0
0
0
0 15 0
0
0
0
0
0
0
0
0
0
0
0
0
0
16
0 ,
0
0
это будет означать, что требуется передать потоки с объемами
информации 2-5 = 16 и 1-3 = 15.
Возможные пути передачи потоков информации удобно представить в
виде деревьев путей. В конкретном случае, если ограничиться только тремя
ярусами (более длинные пути явно нецелесообразны), деревья путей можно
представить в виде, приведенном на рис.7.2.
1
2
5
1
4
2
2
2
3
4
3
4
4
1
3
5
3
3
2
2
3
4
5
5
5
Рис.7.2
В качестве переменных хi целесообразно выбрать величины потоков
информации, передаваемой по i-му пути. Число переменных будет
определяться количеством путей входящих в построенные деревья путей.
Для составления математической модели задачи удобно использовать
таблицу путей где каждому потоку Ф соответствует набор путей с количеством
передаваемой информации хi.
Ф
2-5
1-3
Пути
xi
12
15
2-3-5
2-4-5
2-4-3-5
2-3-4-5
1-2-3
1-5-3
1-2-4-3
1-5-4-3
Пропускные способности ветвей и стоимости
15=51 23=32 24=42 34 43 35=53 45=54
15
20
10
10 10
15
15
x1
x2
x3
x4
x5
x6
x7
x8
5
9
6
6
5
5
3
2
8
7
2
4
3
9
6
4
9
8
8
2
Стоимость
пути
С
14
8
23
14
8
13
17
14
53
Стоимость пути складывается из стоимости передачи единицы
информации по каждому из составляющих ветвей. Так стоимость первого пути
с1 = с23 + + с35 = 14.
Как видно, в таблице объединены двухсторонние ветви, имеющие в обоих
направлениях одинаковые характеристики, и только выделены отдельно ветви
34 и 43, имеющие разную стоимость.
Математическая
модель
задачи
имеет
целевую
функцию,
соответствующую
оптимизации-минимизации
стоимости
передачи
информации:
n
F c i x i min .
(7.11)
i 1
В частности, из таблицы путей следует F = 14x1 + 8x2 + 23x3 + 14x4 + 8x5 +
+ 13x6 + 8x5 + 13x6 + 17x7 + 14x8 min.
В качестве ограничений выступают следующие требования:
1. Суммарный поток информации между заданной парой узлов,
представленный в виде суммы потоков по каждому из путей, должен быть
равен требуемому потоку информации между этой парой узлов, т.е.
х1 + х2 + х3 + х4 = 25 = 16,
х5 + х6 + х7 + х8 = 13 = 15.
(7.12)
2. Для любой ветви сети суммарный поток информации, образованный
путями, проходящими через ветвь, не может превышать пропускной
способности этой ветви, поэтому из таблицы путей следует
х5 + х7 15,
х6 + х8 15,
х1 + х4 + х5 20,
х2 + х3 + х7 10,
х4 10,
(7.13)
х3 + х7 + х8 10,
х1 + х3 + х6 15,
х2 + х4 + х8 15.
хi 0.
3. Потоки информации не могут принимать отрицательных значений, т.е.
Целевая функция (7.11 ) и система ограничений (7. 12) и (7.13 )
позволяют решать и исследовать задачу оптимизации сети связи методом
линейного программирования.