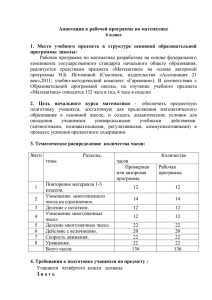
1. Сравнение по модулю с неизвестным.
Общее сравнение по mod m с неизвестным х:
anxn+an-1xn-1+…+a1x1+a0 = 0 (mod m)
где а0, а1, …, аn ∈ Z
2. Решение сравнения
Решением сравнения называется любое целое
число, при подставке которого вместо Х
сравнение (1) становится верным сравнением
целых чисел
3. Сравнения с неизвестным х называются
равносильными, если множества их решений
совпадают.
4. Китайская теорема об остатках. Если m1,
m2, …, mk Є N и попарно взаимно простые, то
система сравнений первой степени:
х ≡ 𝑎1 (𝑚𝑜𝑑 𝑚1 )
х ≡ 𝑎2 (𝑚𝑜𝑑 𝑚2 )
{
…………………..
х ≡ 𝑎𝑘 (𝑚𝑜𝑑 𝑚𝑘 )
1)
2)
1)
2)
3)
4)
имеет единственное решение по модулю m =
m1∙m2∙…∙mk при любых 𝑎1 , 𝑎2 , … , 𝑎𝑘 ∈ 𝑍.
5. Алгоритм решения системы:
из первого сравнения находим
x = a1 + m1∙t (*)
подставив вместо x во второе сравнение (*) и
решив полученное сравнение относительно t,
получим
t = b1 + m2∙y и поэтому x = a1 + m1∙b1 + m1∙m2∙y
3)подставляем найденное значение x в третье
сравнение системы, решаем его и т.д.
6. Отображение 𝜑: 𝑁 → 𝑁, сопоставляющее
каждому числу m Є N число 𝜑(𝑚), равное
количеству натуральных чисел 𝑎 ≤ 𝑚 и взаимно
простых с m, называется функция Эйлера.
Формулы нахождения функции Эйлера:
если число р – простое ⟹ 𝜑(p) = p-1
𝜑(𝑝𝑘 ) = 𝑝𝑘 − 𝑝𝑘−1
∀𝑚, 𝑛 ∈ 𝑁 и взаимно простых 𝜑(𝑚 ∙ 𝑛) = 𝜑(𝑚) ∙
𝜑(𝑛)
если m ∈ N и имеет каноническое разложение:
𝑘
𝑘
𝑘
m = 𝑝1 1 ∙ 𝑝2 2 ∙ … ∙ 𝑝𝑠 𝑠 ⟹
1
1
1
𝜑(𝑚) = 𝑚 (1 − ) (1 − ) … (1 − )
𝑝1
𝑝2
𝑝𝑠
7. Если число а, m ∈ N и взаимно просты (т.е. (a,
m) = 1) ⟹ 𝒂𝝋(𝒎) ≡ 𝟏(𝒎𝒐𝒅 𝒎).
8. Сравнение первой степени: ax≡b(mod m) , где
a, b Є Z
Следствие. Если (a, m) = 1, то сравнение имеет
единственное решение по mod m (по т. Эйлера
𝒙 ≡ 𝒃 ∙ 𝒂𝝋(𝒎)−𝟏 ).
9. Если (а, m) = d , то сравнение разрешимо тогда
и только тогда, когда d /b и сравнение имеем d
решений по mod m.
10. Квадратный вычет и невычет
Целое число а, взаимно простое с р, называется
квадратным вычетом по модулю р, если
квадратное сравнение 𝑥 2 ≡ а(𝑚𝑜𝑑 р) имеет
решение , и квадратным невычетом по модулю
р в противном случае.
11. Если a Є Z, (a, р) = 1, то а является
квадратным вычетом по простому модулю р>
р−1
2, тогда и только тогда, когда а 2 ≡ 1( 𝑚𝑜𝑑 р) и
а является квадратным невычетом по простому
модулю р> 2, тогда и только тогда, когда
р−1
а 2 ≡ −1( 𝑚𝑜𝑑 р).
12. Пусть A, B, C – тройка непустых
множеств.
Бинарной операцией в паре A, B со значениями
в C называется отображение P->C, где P ⊂AxB
13. Бинарная операция наз-тся коммутативной,
если её результат не зависит от перестановки
операндов.
Ассоциативной – если результат не зависит от
порядка вычисления (расстановки скобок)
14. Алгеброй A называется совокупность <M,S>
множества М с заданными в нем операциями
S= {f1,f2,…,fn},
где множество М – носитель, S – сигнатура
алгебры.
Обозначение A=⟨M,S⟩
Пример: на множестве целых чисел определены
операции сложения и умножения по модулю n
(остатки от деления на n)
15. Группа – непустое мн-во G, в котором
определена алгебраическая операция –
умножение
Примеры:
- Мн-во G двух элементов а и е с операцией,
заданной равенствами ее=аа=е, еа=ае=а, явл.
группой
- все рациональные, действительные и
комплексные числа, исключение 0, явл.
группами относительно операции умножения
чисел
Абелева группа (коммутативная) – группа, в
которой групповая операция явл.
коммутативной.
16. Простейшее свойства групп.
1. В группе Ge нейтральный элемент и Ɐx Є Ge
симметричный элемент
2. Для Ɐu, V Є G уравнения u*x=v, y*u=v имеют
единственное решение:
X= u-1 * v, y=v*u-1
3, Закон сокращение в группе: Если u*x=u*y, то
x=y
17. Полем называют кольцо P, обладающее след.
свойствами:
- Р содержит по крайней мере 1 элемент,
отличный от нуля
- для любых a,b из Р, где а≠0, уравнение ах=b
имеет решение т.е. существует такой элемент
qЄP, a*q=b.
Примеры полей: рациональные, действительные,
комплексные
18. Полем называется кольцо P, обладающее
следующими свойствами:
1. (Обратимость умножения) Для любых a и b из
P, где a ≠ 0, уравнение ax = b имеет (по крайней
мере одно) решение, т. е. существует элемент
такой, что aq = b.
2. P содержит по крайней мере один элемент,
отличный от нуля.
19. Кольцо – непустое мн-во R, в котором
определены 2 алгебраические операции:
сложение и умножение.
Примеры колец: 1. Мн-во целых чисел, 2. Мн-во
рацион-ых чисел, 3. Мн-во действит. чисел.
20. Коммутативность сложения а+b=b+a
Коммутативность умножения ab=ba
Ассоциативность сложения (a+b)+c=a+(b+c)
Ассоциативность умножения (ab)*c=a*(bc)
Обратимость сложения
Дистрибутивность умножения относительно
сложения (a+b)*c=ac+bc