Свойства определенного интеграла

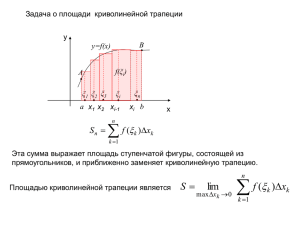
Свойства определенного интеграла.
Используя определение предела интегральных сумм, получаем следующие свойства
определенного интеграла:
1) Если f(x) и g(x)  a, b ,
  f ( x)    g ( x)  a, b
b
, 
и
b
-
произвольные числа,
справедливо
то
функция
равенство:
b
   f ( x)    g ( x)dx     f ( x)dx     g ( x)dx
a
a
2) Если f(x)  a, b , то
a
b
a
a
b
 f ( x)dx   f ( x)dx
3) Если f(x)  a, b и c  a, b , то f(x)  a, c , f(x)  c, b и справедливо
b
c
b
a
a
c
 f ( x)dx   f ( x)dx   f ( x)dx
равенство:
4) Если f(x)  a, b , f ( x )  0, x  a, b и b>a, то справедливо неравенство:
b
 f ( x)dx  0
a
5) Если f(x) и g(x)  a, b , f ( x)  g ( x) x  a, b и b>a, то справедливо неравенство:
b
b
a
a
 f ( x)dx  g ( x)dx
6) Если f(x)  a, b и M  sup  f ( x)  , m  inf  f ( x) , b>a, то выполняются неравенства:
a ,b 
a ,b 
b
m(b  a)   f ( x)dx  M (b  a)
a
f(x)  Сa, b ,
7) Если
то
c a, b ,
такое,
что
выполняется
равенство:
b
 f ( x)dx  f (c)(b  a)
a
Доказательство свойств.
1) 1) Напишем интегральную сумму для функции   f ( x)    g ( x) :
n
n
n
S 2     f ( k )    g ( k )   xk  xk 1     f ( k )   xk  xk 1     g ( k )   xk  xk 1  .
k 1
k 1
k 1
n
n
k 1
k 1
Обозначим S1   f ( k )  xk  xk 1  и S 2   g ( k )  xk  xk 1  .
Тогда получим равенство: S    S1    S 2 .
b
b
Так как lim S1   f ( x)dx и lim S 2   g ( x)dx, то S   lim S1   lim S 2 и по
d (T )0
d (T )0
a
d (T )0
b
определению он равен
d (T )0
a
   f ( x)    g ( x)dx, что и доказывает свойство 1.
a
n
2) Напишем интегральную сумму для f(x): S   f ( k )  xk  xk 1  .
k 1
Обозначим xs  xns , s=0,…,n и  s   ns , s=1,…,n.
Тогда x0  b  x1  ...  xn  a и  s  xs , xs 1 .
В интегральной сумме S заменим k=n-s:
n
n
n
s 1
s 1
S   f ( n s )  ( xn s  xn s 1 )   f ( s )  ( xs  xs 1 )   f ( s )  ( xs 1  xs )   S .
s 1
n
По определению S    f ( s )  ( xs 1  xs ) есть интегральная сумма для интеграла
s 1
b
 f ( x)dx, что и доказывает свойство 2.
a
3) Без доказательства.
n
4) Из неравенства: f ( x )  0, b>a, следует, что S   f ( k )   xk  xk 1   0 и lim S  0.
d (T )0
k 1
5) Так
как
f ( x)  g ( x)  0,
то
из
свойств
b
b
b
b
b
a
a
a
a
a
1
и
4
следует,
что
0    f ( x)  g ( x) dx   f ( x)dx   g ( x)dx  f ( x)dx  g ( x)dx.
6) Так как m  f ( x)  M , x a, b, то интегрируя эти неравенства, ввиду свойства 5,
b
получим: m(b  a)   f ( x)dx  M (b  a).
a
7) Так как f(x)  Сa, b , то f(x)  a, b (это будет доказано в следующем параграфе).
b
Из свойства 6 следует, что m 
 f ( x)dx
 M , где M  max f ( x) и m  min f ( x).
ba
a ,b 
a ,b 
По теореме о промежуточном значении непрерывной на отрезке функции ca,b,
a
b
такая,
что
f (c ) 
 f ( x)dx
a
ba
b
или
 f ( x)dx  f (c)  (b  a).
a
Замечание
Это свойство обычно называют теоремой о среднем.
Критерий интегрируемости функций на отрезке. Интегрируемость
непрерывных и монотонных функций.
Пусть задано некоторое разбиение T отрезка [a, b]: a=x0<x1<…<xn=b. Пусть f(x)  a, b .
Тогда по доказанному ранее f(x) ограничена на [a, b] и, следовательно, f(x) ограничена на
каждом из отрезков разбиения [xk-1, xk], k=1,…,n.
Обозначим M  sup  f ( x) , m  inf  f ( x) , k=1,…,n.
 xk 1 , xk 
 xk 1 , xk 
n
S   M k ( xk  xk 1 )
k 1
n
S   mk ( xk  xk 1 )
k 1
Суммы S и S называются соответственно верхняя и нижняя суммы Дарбу.
Критерий интегрируемости
f ( x)  a, b  lim( S  S )  0 (без доказательств).
d (T )0
Теорема об интегрируемости непрерывных функций.
Пусть f(x)  Сa, b. Тогда f(x)  a, b.
Доказательство.
По теореме Кантора о равномерной непрерывности непрерывной на отрезке функции:
  0  0x1 , x2  a, b: x1  x2    f ( x1 )  f ( x2 )  
Пусть разбиение T отрезка [a, b] имеет диаметр d (T )   . Тогда из равномерной
непрерывности функции f(x) на [a, b] следует, что M k  mk   , k=1,…,n.
Запишем разность S и S в виде суммы:
n
n
k 1
k 1
0  S  S   ( M k  mk )  ( xk  xk 1 )    ( xk  xk 1 )   (b  a ).
Следовательно
lim ( S  S )  0 и по критерию интегрируемости f(x)  a, b. Теорема
d (T ) 0
доказана.
Теорема об интегрируемости монотонных на отрезке функций.
Пусть f(x) – монотонная на отрезке [a, b] функция. Тогда f(x)  a, b.
Доказательство.
Предположим для определенности, что f(x) – неубывающая на [a, b] функция. Пусть T –
некоторое разбиение [a, b].
Тогда, ввиду неубывания f(x), Mk=f(xk) и mk=f(xk-1).
Следовательно, разность S - S можно оценить следующим образом:
n
n
n
k 1
k 1
k 1
0  S  S   ( M k  mk )  ( xk  xk 1 )    f ( xk )  f ( xk 1 )   ( xk  xk 1 )  d (T )    f ( xk )  f ( xk 1 )  
 d (T )   f (b)  f (a)  0 d (T )  0 .
По критерию интегрируемости f(x)  a, b. Теорема доказана.