Решения уравнений с параметром

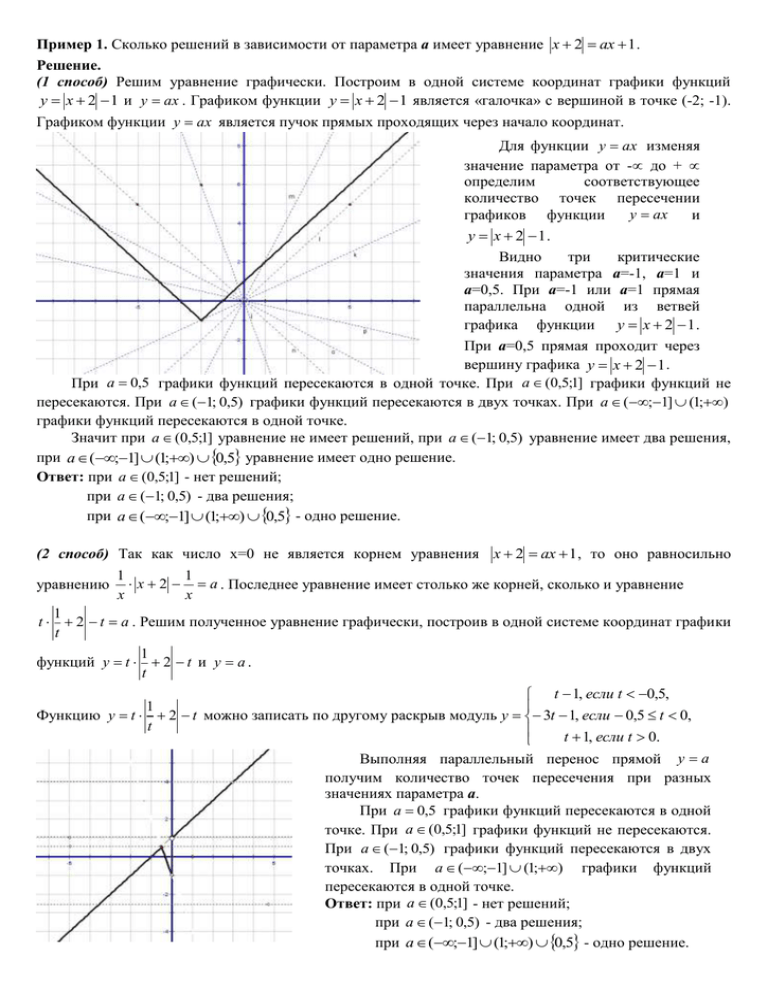
Пример 1. Сколько решений в зависимости от параметра а имеет уравнение х  2  ах  1 .
Решение.
(1 способ) Решим уравнение графически. Построим в одной системе координат графики функций
у  х  2  1 и у  ах . Графиком функции у  х  2  1 является «галочка» с вершиной в точке (-2; -1).
Графиком функции у  ах является пучок прямых проходящих через начало координат.
Для функции у  ах изменяя
значение параметра от - до + 
определим
соответствующее
количество точек пересечении
у  ах
графиков функции
и
у  х  2  1.
Видно
три
критические
значения параметра а=-1, а=1 и
а=0,5. При а=-1 или а=1 прямая
параллельна одной из ветвей
графика функции у  х  2  1 .
При а=0,5 прямая проходит через
вершину графика у  х  2  1 .
При а  0,5 графики функций пересекаются в одной точке. При а  (0,5;1] графики функций не
пересекаются. При а  (1; 0,5) графики функций пересекаются в двух точках. При а  (;1]  (1;)
графики функций пересекаются в одной точке.
Значит при а  (0,5;1] уравнение не имеет решений, при а  (1; 0,5) уравнение имеет два решения,
при а  (;1]  (1;)  0,5 уравнение имеет одно решение.
Ответ: при а  (0,5;1] - нет решений;
при а  (1; 0,5) - два решения;
при а  (;1]  (1;)  0,5 - одно решение.
(2 способ) Так как число х=0 не является корнем уравнения х  2  ах  1 , то оно равносильно
уравнению
1
1
 х  2   а . Последнее уравнение имеет столько же корней, сколько и уравнение
х
х
1
t   2  t  а . Решим полученное уравнение графически, построив в одной системе координат графики
t
1
функций у  t   2  t и у  а .
t
 t  1, если t  0,5,
1

Функцию у  t   2  t можно записать по другому раскрыв модуль у   3t  1, если  0,5  t  0,
t

t  1, если t  0.

Выполняя параллельный перенос прямой у  а
получим количество точек пересечения при разных
значениях параметра а.
При а  0,5 графики функций пересекаются в одной
точке. При а  (0,5;1] графики функций не пересекаются.
При а  (1; 0,5) графики функций пересекаются в двух
точках. При а  (;1]  (1;) графики функций
пересекаются в одной точке.
Ответ: при а  (0,5;1] - нет решений;
при а  (1; 0,5) - два решения;
при а  (;1]  (1;)  0,5 - одно решение.
Пример 2. Найдите все значении параметра а, при которых уравнение х2  4х  х  а  2  а  0 имеет
четыре решения.
Решение.
Решим уравнение графически. Раскроем модуль и рассмотрим два случая:
Если х  а , то уравнение можно записать в виде а  ( х  1)2  1 .
1
7
Если х  а , то уравнение можно записать в виде а  ( х  3) 2  .
3
3
В одной системе координат хОа построим графики функций: график функции а  ( х  1)2  1 только ту
1
7
часть, которая расположена ниже прямой а  х и график функции а  ( х  3) 2  только ту часть,
3
3
которая расположена выше прямой а  х .
По рисунку видно что прямая параллельная оси Ох
пересекает график уравнения в четырех точках при
 7

а    ;  2 .
 3

Следовательно исходное уравнение имеет четыре
 7

решения при а    ;  2  .
 3

 7

Ответ: а    ;  1
 3

Пример
3.
значении
параметра
а,
при
которых
уравнение
18
( х 2  6 х  а) 2  12( х 2  6 х  а) 2  37  cos
имеет ровно два корня.
а
Решение. (1 способ) Уравнение равносильно уравнению
2
18
18 

( х 2  6 х  а) 2  12( х 2  6 х  а) 2  36  1  cos
0

х 2  6 х  а  6  1  cos
или
0.
а
а 

2
18
 1 то
Выражение х 2  6 х  а  6
неотрицательно при всех значениях х. А т.к.  1  cos
а
18
0  1  cos
 2 . Сумма двух неотрицательных выражений равно нулю тогда и только тогда, когда оба
а
выражения одновременно равны нулю, т.е.
 х 2  6 х  а  6  0,
а  х 2  6 х  6,
 а  х 2  6 х  6,
а  х 2  6 х  6,




18
18


18
 9
1  cos
 0.
cos
 1.
 2n, n  . 
 n, n  .



а
а


 а
 а
Решим первое уравнение а  х2  6 х  6 системы графически и выясним, при каких значениях

Найдите
все

параметра а уравнение имеет ровно два корня. Построим графики функций у  х2  6 х  6 и у  а в
одной системе координат.
Графики функций у  х 2  6 х  6  0 и у  а
пересекаются в двух точках при а  (6;  )   3.
Выясним, при каких значениях параметра
а  (6;  )   3 второе равенство системы верно.
9
9
 n, n   . Так как n   , то и   , т.е. а   1;  3;  9.
а
а
Из полученных значений параметра а   1;  3;  9
удовлетворяют условию а  (6;  )   3 только
а   3; 9. Значит, исходное уравнение имеет ровно два
корня при а   3; 9. Ответ: а   3; 9.
(2 способ) Уравнение равносильно уравнению
18
( х 2  6 х  а) 2  12( х 2  6 х  а) 2  36  1  cos
0
а
Выражение
х
2
6 х а6

2
2
18 

 6 х  а  6  1  cos
0.
а 

18
 1 то
неотрицательно при всех значениях х. А т.к.  1  cos
а
или
х
2
18
 2 . Сумма двух неотрицательных выражений равно нулю тогда и только тогда, когда оба
а
выражения одновременно равны нулю, т.е.
 х 2  6 х  а  6  0,
 х 2  6 х  6  а  0,


18

 9
1  cos
 0.
 n, n  .


а

 а
Решим первое уравнение х2  6 х  6  а  0 . Данное уравнение будет иметь два решения, если
0  1  cos
уравнение t 2  6t  6  а  0 имеет один положительный корень или два корня один из которых
положительный, а другой отрицательный.
1) Уравнение t 2  6t  6  а  0 имеет один корень, т.е. D  12  4a  0 , a  3 , х  3 , удовлетворяет
условию. Значит, при a  3 уравнение t 2  6t  6  а  0 имеет один положительный корень,
следовательно уравнение х2  6 х  6  а  0 имеет ровно два корня.
2) Уравнение t 2  6t  6  а  0
имеет два корня один из которых положительный, а другой
 D  0,
12  4а  0, а  3,
отрицательный. Данное условие выполняется, если 
т.е. 
а 6.

 6  а  0;  а  6;
 x1  x2  0;
Получили, что уравнение х2  6 х  6  а  0 имеет ровно два корня при а  (6;  )   3.
Выясним, при каких значениях параметра а  (6;  )   3 второе равенство системы верно.
9
9
 n, n   . Так как n   , то и   , т.е. а   1;  3;  9.
а
а
Из полученных значений параметра а   1;  3;  9 удовлетворяют условию а  (6;  )   3 только
а   3; 9. Значит, исходное уравнение имеет ровно два корня при а   3; 9.
Ответ: а   3; 9.
Пример 4. Решить уравнение 3х  3  ах2  4 , где а параметр.
Решение.
Решим данное уравнение графически: у  3х  3 ; у  ах 2  4 .
Графиком функции у  3 х  1 является «галочка» с вершиной в точке (-1; 0). Графиком функции
у  ах 2  4 является семейство парабол с вершиной в точке (4; 0). Критическими точками для параметра
а являются точка (-1; 0) и точки касания параболы прямых у  3 х  3 и у  3 х  3 . Парабола проходит
через точку (-1; 0) при а  4 . Найдем точку касания параболы у  ах 2  4 с прямой у  3 х  3 :
3
9
у  2ах , 2ах  3 , х0 
4
, у0 
2а
4а
9
3
9
 4  3
3, а  .
4а
2а
4
Найдем точку касания параболы у  ах 2  4 с прямой у  3х  3 :
9
3
9
9
 3 
у  2ах , 2ах  3 , х0  
 4,
 4  3      3 , а 
, у0 
.
2а
4а
28
4а
 2а 
Если а  4 , то парабола пересекает только прямую у  3 х  3 , и при этих значениях параметра а
корнями исходного уравнении будут корни
3  9  4а
уравнения 3 х  3  ах 2  4 , откуда х 
.
2а
Если  4  а  0 , то парабола пересекает
прямые у  3 х  3 и у  3 х  3 , и меньший из
корней получается при пересечении параболы с
прямой у  3 х  3 , т.е. это меньший корень
 3  9  28а
,а
2а
второй больший корень получается при
пересечении параболы с прямой у  3 х  3 , т.е. это
больший корень уравнения 3х  3  ах 2  4 ,
3  9  4а
х
.
2а
уравнения  3х  3  ах 2  4 , х 
Если а  0 , то исходное уравнение принимает вид 3х  3  ах2  4 , корнями которого являются
7
1
и х .
3
3
9
Если 0  а 
, то парабола пересекает прямые у  3 х  3 и у  3 х  3 , и каждую из них в двух
28
точках. Значит корнями исходного уравнения являются корни уравнений  3х  3  ах 2  4 и
 3  9  28а
3  9  4а
3 х  3  ах 2  4 , откуда получаем х 
и х
.
2а
2а
9
9
Если
 а  , то парабола пересекает только прямую у  3 х  3 . Значит корнями исходного
28
4
3  9  4а
уравнения являются корни уравнения 3 х  3  ах 2  4 , откуда получаем х 
.
2а
9
Если а  , то парабола графики функций не пересекаются, соответственно исходное уравнение
4
не имеет решений.
 3  9  28а
3  9  4а
3  9  4а
Ответ: если а  4 , то х 
;
если  4  а  0 , то х 
, х
;
2а
2а
2а
 3  9  28а
3  9  4а
7
1
9
если а  0 , то х   и х  ;
если 0  а 
, х
и х
;
2а
3
3
2а
28
3  9  4а
9
9
9
 а  , то х 
если
;
если а  , то нет решений.
2а
28
4
4
числа х  
Пример 5. При каких значениях параметра а уравнение х  а  2 2 х  а 2 имеет решения? Определить
число решений уравнения.
Решение.
(1 способ) Построим в одной системе координат графики функций у  х  а и у  2 2 х  а 2 .
 а2 
у  2 2 х  а ; если х  0 , то у  2 2 х  а ,  ; 0  и 0; 2а 2  - точки пересечения с осями координат;
 2 
 а2 
если х  0 , то у  2  2 х  а 2 ,   ; 0  и 0; 2а 2  - точки пересечения с осями координат.
 2 
у  х  а ; а; 0 и 0;  а - точки пересечения с осями координат.
2
2
а2
 а , т.е. а  (0; 2) , то исходное уравнение не
2
имеет решений.
 а2

а2
 a  0 a  
а 2 
2)Если 0  a  ,  2
и 
2 ,
2  2
2

2 a   a
2 a   a
1)Если
 1 
т.е. а  (; 2)    ; 0   (2;  ) , то исходное уравнение
 2 
имеет два решения.
 а2 
Если прямая у  х  а проходит через точки   ; 0  или 0; 2а 2 , то исходное уравнение имеет три
 2 
решения. Подставляя координаты данных точек в уравнение прямой у  х  а получим, что
1
а   , а  2 - значения параметра при которых исходное уравнение имеет три решения.
2

а2
1
a  

Если 
2 , т.е. а    2;   , то исходное уравнение имеет четыре решения.
2

2 a 2   a

Ответ: если а  (0; 2) , то нет решений;
 1 
если т.е. а  (; 2)    ; 0   (2;  ) , то два решения;
 2 
1
если а   , а  2 , то три решения;
2
1

если а    2;   , то четыре решения.
2

(2 способ) Найдите все значения параметра а уравнение при каждом из которых уравнение
х  а  2 2 х  а 2 имеет три различных корня. Найдите эти корни.


 х  0,
1)Пусть х  0 , тогда будем иметь систему 
Чтобы решить эту систему нужно
2
 х  а  2  2 х  а .
рассмотреть два случая:

 х  0,
 х  0,


2
2
1а)  2 х  а  0,
 2 х  а  0,
 х  а  2(2 х  а 2 ); 
1

 х  (2а 2  а ).
3

Подставим полученное значение х в неравенство системы. Будем иметь:
1
2
1

 3 (2а  а )  0,
а   , a  0,


2

1
1
 2
2
2
Отсюда следует, что при  2  а   , х  (2а 2  а ) .
 (2а  а )  а  0,  2  а  0,
2
3
 3

1
2
1

 х  (2а  а ).
2
3

 х  3 (2а  а );


 х  0,

2
 2 х  а  0,

1
 х  (а  2а 2 ).
5

Подставим полученное значение х в неравенство системы. Будем иметь:
1
2
1

 5 (а  2а )  0,
а  0, a  ,


2

1
 2
2
2
Отсюда следует, что при  2  а  0 , х  ( а  2а 2 ) .
 (а  2а )  а  0,  2  а  0,
5

 5
1
2
1
 х  (а  2а ).

2
5

 х  5 (а  2а );

 х  0,
2)Пусть х  0 , тогда будем иметь систему 
Чтобы решить эту систему нужно
2
 х  а  2 2 х  а .
рассмотреть два случая:
 х  0,

1б)  2 х  а 2  0,
 х  а  2(2 х  а 2 );


 х  0,
 х  0,

2

2 х  а  0,
2а) 2 х  а 2  0,
 х  а  2(2 х  а 2 ); 
1

 х  ( 2а 2  а ).
5

Подставим полученное значение х в неравенство системы. Будем иметь:
1
2
1

 5 (2а  а)  0,
а   , a  0,


2

1
1
2
2
2
а

0
,
a  2,
Отсюда следует, что при а   , a  2 , х  (2а 2  а ) .
(
2
а

а
)

а

0
,


2
5

5
1
2
1
 х  (2а  а).

2
5

 х  5 (2а  а);


 х  0,
 х  0,


2
2б) 2 х  а 2  0,
2 х  а  0,
 х  а  2(2 х  а 2 ); 
1

 х  (2а 2  a ).
3

Подставим полученное значение х в неравенство системы. Будем иметь:
1
2
1

 3 (2а  a)  0,
а  0, a  ,


2

1
2
2
2
Отсюда следует, что при а  0, a  2 , х  (2а 2  а ) .
 (2а  a)  а  0, а  0, a  2,
3

3
1
2
1
 х  (2а  a).

2
3

 х  3 (2а  a);

1
1
Ответ: если  2  а   , то х  (2а 2  а ) ;
2
3
1
если  2  а  0 , то х  ( а  2а 2 ) ;
5
1
1
если а   , a  2 , то х  (2а 2  а ) ;
2
5
1
если а  0, a  2 , то х  (2а 2  а ) .
3