cu s ag

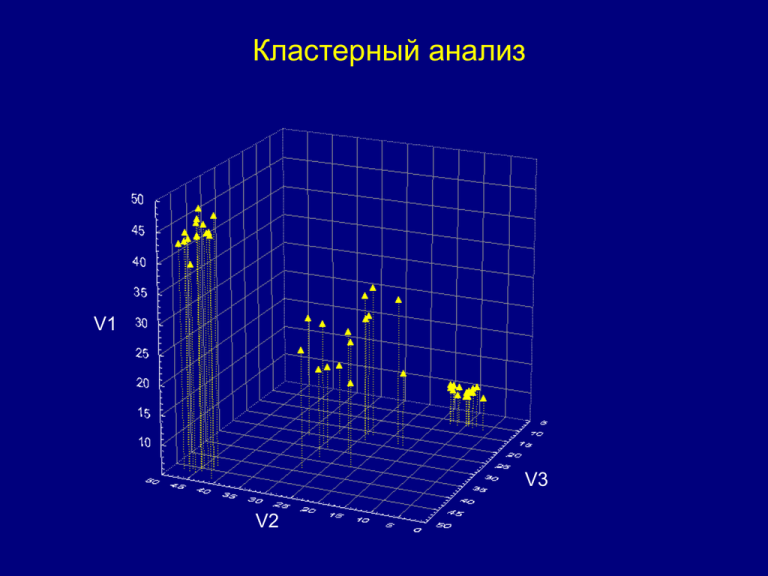
Кластерный анализ
V1
V3
V2
Кластерный анализ – это разбиение множества объектов
на подмножества, называемые кластерами, так, чтобы каждый
кластер состоял из схожих объектов, а объекты разных кластеров
существенно отличались друг от друга.
Кластер 1
V1
V2
Кластер 2
V3
V1
Кластер 3
V3
V2
Группировка наблюдений осуществляется на основе мер сходства.
Чаще всего в качестве такой меры используется
Евклидово расстояние (геометрическое
расстояние в многомерном пространстве):
d x, y 
Объект
X (Cux,Sx, Agx)
m
2
(
x

y
)
 i i
i 1
d x , y - расстояние между объектами x и y;
xi , yi - значения i-ого свойства объектов x и y
d x, y
dAg
Объект
Y (Cuy,Sy, Agy)
m - количество свойств
2
2
d x, y  dCu
 d S2  d Ag
d x, y  (Cux  Cu y ) 2  ( S x  S y ) 2  ( Ag x  Ag y ) 2
Расстояние между объектами зависит от масштаба по осям.
Объект
Cu
S
Ag
1.4
44.2
3.9
1.04
18.7
0.7
X (Cux,Sx, Agx)
d 2Ag  (3,9  0,7) 2  10,24
d x, y
d Cu2  (1,04  1,4) 2  0,13
dAg
Объект
Y (Cuy,Sy, Agy)
d s2  (44,2  18,7) 2  650,25
650,25 / 660,62 *100  98%
d  10,24  0,13  650,25  25,7
В этом примере расстояние между объектами будет определяться в основном разницей
содержаний серы.
Медь и серебро практически не будут учтены при выделении кластеров поскольку их
содержания на порядок меньше, чем содержания серы.
Чтобы сделать масштабы по осям одинаковыми, перед кластеризацией
исходные выличины нормируют, используя одну из следующих формул:
x  xmin
xnorm 
xmax  xmin
Объект
x  xmin
xnorm  1  2
xmax  xmin
X (Cux,Sx, Agx)
d x, y
dAg
Объект
Y (Cuy,Sy, Agy)
xnorm 
xnorm
cu
s
ag
-0.56
1.25
-0.35
-0.87
-0.95
-1.47
- стандартизированные значения
x

x
xx
s
(стандартизация)
(нормировка на среднее)
x0
Нормированные значения
d 2Ag  (0,35  1,47) 2  1,25
cu
s
ag
-0.56
1.25
-0.35
-0.87
-0.95
-1.47
d Cu2  (0,56  0,87) 2  0,096
d s2  (1,25  0,95) 2  4,88
d  1,25  0,096  4,88  2,5
Оригинальные значения
Cu
S
Ag
1.4
44.2
3.9
1.04
18.7
0.7
d  10,24  0,13  650,25  25,7
Помимо Евклидова расстояния в алгоритмах кластеризации используется
Манхэттенское расстояние
m
d x , y   | xi  yi |
i 1
Объект
X (Cux,Sx, Agx)
cu
s
ag
-0.56
1.25
-0.35
-0.87
-0.95
-1.47
d Ag | 0,35  1,47 | 1,12
d x, y
dAg
Объект
Y (Cuy,Sy, Agy)
d Cu | 0,56  0,87 |  0,31
d s | 1,25  0,95 |  2,2
d  1,12  0,31  2,2  3,63
В большинстве случаев эта мера расстояния приводит к таким же результатам, что
и Евклидово, однако влияние выбросов уменьшается (так как они не возводятся в
квадрат).
Расстояние Мехаланобиса
Интуитивное объяснение
Рассмотрим задачу определения вероятности того, что некоторая точка в N-мерном
евклидовом пространстве принадлежит множеству, которое задано набором точек, определённо
принадлежащих данному множеству. Найдем центр масс множества. Интуитивно понятно, что чем
ближе заданная точка к центру масс, тем больше вероятность того, что она принадлежит множеству.
Однако также стоит учитывать, на какого размера области рассредоточены точки множества, чтобы
понять, насколько значимо расстояние между заданной точкой и центром масс. Самый простой
подход заключается в вычислении среднеквадратичного отклонения точек множества от центра масс.
Если расстояние между заданной точкой и центром масс меньше среднеквадратичного отклонения,
то можно заключить, что вероятность принадлежности точки множеству высока. Чем дальше точка,
тем больше вероятность того, что она не принадлежит множеству.
Этот интуитивный подход можно определить математически в нормальное распределение через
расстояние между заданной точкой и множеством по формуле (x-µ)/σ . С помощью подстановки этого
значения можно найти вероятность принадлежности точки множеству.
Недостаток такого подхода заключается в использовании предположения о том, что точки множества
сферически распределены вокруг центра масс (то есть равномерно по всем измерениям). Если же
распределение явно не сферическое (например, эллипсоидальное), то было бы естественным
учитывать в вероятности принадлежности не только расстояние до центра масс, но и направление на
него. В направлении короткой оси эллипсоида заданная точка должна быть ближе к центру масс,
чтобы принадлежать множеству, в то время как в направлении длинной оси она может быть дальше.
Для записи этого в математическом виде эллипсоид, лучшим образом представляющий
вероятностное распределение множества, может быть задан матрицей ковариаций множества.
Расстояние Махаланобиса — это просто расстояние между заданной точкой и центром масс,
делённое на ширину эллипсоида в направлении заданной точки.
Материал из Википедии:
http://ru.wikipedia.org/wiki/%D0%E0%F1%F1%F2%EE%FF%ED%E8%E5_%CC%E0%F5%E0%EB%E0%
ED%EE%E1%E8%F1%E0
Для данных, измеренных в номинальной или порядковой шкалах
используется мера Процент несогласия:
m
d x, y 
x
i 1
i
 yi
m – количество признаков
m
Зернистость
Сортировка
цвет
пористость
кварц
1
крупнозернистый
плохая
серый
высокая
много
1
0
2
мелкозернистый
хорошая
серый
средняя
мало
2
0,8
0
3
среднезернистый
хорошая
серый
низкая
мало
3
0,8
0,4
1
2
3
0
Существует большое разнообразие алгоритмов кластеризации.
По способу разделения множества наблюдений на классы, их можно разделить 2 типа:
иерархический и итерационный.
Иерархическая кластеризация.
Иерархические методы – это комплекс алгоритмов, использующих разделение
крупных кластеров на более мелкие или объединение мелких в более крупные.
Соответственно, выделяют кластеризации
разделительную (дивизивную)
и
агломеративную (объединительную)
Существует большое количество алгоритмов кластеризации. Это связано с
тем, что матрица расстояний может быть получена с помощью
разнообразных метрик: евклидовой, Махаланобиса, семейства метрик
Минковского и т.д. Выбор метрики производится самим исследователем.
После вычисления матрицы расстояний начинается процесс агломерации
(от латинского agglomero - присоединяю, накапливаю), проходящий
последовательно шаг за шагом. На первом шаге этого процесса два
исходных наблюдения (монокластера), между которыми самое
минимальное расстояние, объединяются в один кластер, состоящий уже из
двух объектов (наблюдений). Таким образом, вместо бывших N
монокластеров (кластеров, состоящих из одного объекта) после первого
шага останется N-1 кластеров, из которых один кластер будет содержать
два объекта (наблюдения), а N-2 кластеров будут по-прежнему состоять
всего лишь из одного объекта. Отметим, что на втором шаге возможны
различные методы объединения между собой N-2 кластеров. Это вызвано
тем, что один из этих кластеров уже содержит два объекта.
По этой причине возникает два основных вопроса:
1. как вычислять координаты такого кластера из двух (а далее и более двух)
объектов;
2. как вычислять расстояние до таких "полиобъектных" кластеров от
"монокластеров" и между "полиобъектными" кластерами.
Методы связывания кластеров:
Одиночная связь (метод ближайшего соседа). Расстояние между двумя
кластерами определяется расстоянием между двумя наиболее близкими
объектами (ближайшими соседями) в различных кластерах.
Результирующие кластеры имеют тенденцию быть представленными
длинными "цепочками."
As Cr Mn Cu Pb Ni Zn Fe V Ti
Полная связь (метод наиболее удаленных соседей).
Расстояния между кластерами определяются
наибольшим расстоянием между любыми двумя
объектами в различных кластерах (т.е. "наиболее
удаленными соседями ").
As Cu Mn Cr Pb Ni Zn Fe V Ti
Невзвешенное попарное среднее.
Расстояние между двумя различными
кластерами вычисляется как среднее
расстояние между всеми парами объектов
в них. Метод хорошо работает как в
случаях хорошо обособленных кластеров,
так и в случаях протяженных (цепочного
типа) кластеров.
As Cr Cu Mn Pb Ni Zn Fe V Ti
Взвешенное попарное среднее.
Отличается от невзвешенного тем, что при
вычислениях размер соответствующих
кластеров (т.е. число объектов, содержащихся
в них) используется в качестве весового
коэффициента. Используется, когда
предполагаются неравные размеры кластеров.
As Cu Cr Mn Pb Ni Zn Fe V Ti
Невзвешенный центроидный метод.
Расстояние между двумя кластерами
определяется как расстояние между их
центрами тяжести.
As Cr Cu Mn Ti V Pb Ni Zn Fe
Взвешенный центроидный метод.
Отличается от невзвешенного тем, что
при вычислениях используются веса
для учёта разницы между размерами
кластеров (количество объектов).
Cr As Cu Mn V
Ti Pb Ni Zn Fe
Метод Варда.
As Cu Mn Cr
Pb
Ni
Zn Fe
V
Ti
Этот метод использует методы дисперсионного анализа для оценки
расстояний между кластерами. Метод минимизирует сумму квадратов
(SS) для любых двух (гипотетических) кластеров, которые могут быть
сформированы на каждом шаге. В целом метод представляется очень
эффективным, однако он стремится создавать кластеры малого размера.
As Cu Mn Cr
Pb
Ni
Zn Fe
V
Ti
Итерационная кластеризация.
Среди методов итерационной классификации наиболее часто используемым
является метод К-средних.
Метод K средних строит ровно k различных кластеров, расположенных на
возможно больших расстояниях друг от друга. Вычисления начинаются с k
случайно выбранных наблюдений, которые становятся центрами групп, после
чего объектный состав кластеров меняется с целью минимизации
изменчивости внутри кластеров и максимизации изменчивости между
кластерами.
Программа перемещает объекты (т.е. наблюдения) из одних групп
(кластеров) в другие для того, чтобы получить наиболее значимый результат
в соответствии с критерием дисперсионного анализа (максимальное
отношение межгрупповой дисперсии к внутригрупповой).
Значения F-статистики, полученные для каждого измерения, является
индикатором того, насколько хорошо соответствующая переменная
дискриминирует кластеры.
Схема выделения кластеров методом К-средних.
Недостатками метода К-средних являются:
непонятно, как выбирать исходные центры кластеров
число кластеров надо знать заранее
Критерием адекватной кластеризации может служить
пространственная обособленность кластеров.
Устойчивая, реально существующая кластеризация сохраняется при
изменении методов кластеризации. Результаты иерархического
кластерного анализа можно проверять итеративным кластерным
анализом по методу k-средних. Если сравниваемые классификации
групп имеют долю совпадений более 70 % (более 2/3 совпадений), то
кластерное решение принимается.
Независимо от предмета изучения, применение кластерного анализа
предполагает следующие этапы:
- отбор выборки для кластеризации.
- определение множества переменных, по которым будут оцениваться
объекты в выборке.
- вычисление значений той или иной меры сходства между объектами.
- применение метода кластерного анализа для создания групп сходных
объектов.
- проверка достоверности результатов кластерного решения.
Кластерный анализ не является статистическим методом, поэтому
проверка статистической значимости неприменима
Кластерный анализ предъявляет следующие требования к данным:
- переменныые должны быть нормированиы;
- распределение переменных должно быть близко к нормальному;
- выборка не должна содержать «выбросов».
Пример 1
В таблице приведены содержания химических элементов в пробах
метасоматитов по одному из потенциально золотоносных участков.
Требуется выделить ассоциации взаимосвязанных элементов.
В качестве меры сходства будем использовать величину, равную 1 – r
( r- коэффициент корреляции Пирсона).
Условия применения коэффициента корреляции Пирсона –
однородность выборки
отсутствие выбросов
распределение, близкое к нормальному
Однородность выборки и отсутствие выбросов можно оценить, построив
матричный график:
Явных выбросов и неоднородности выборок не наблюдается, однако
гистограммы показывают, что у Ag,Pb, Sn, As, Sb, Au и K распределение
существенно отличается от нормального.
Распределение логарифмов этих переменных близко к нормальному,
поэтому для вычисления коэффициентов корреляции будем использовать
логарифмы.
Результаты иерархической кластеризации
по частично преобразованным данным
по исходным данным
(распределение переменных близко к
нормальному)
(распределение переменных значительно
отличается от нормального)
K
Au Pb Ag
K
Au As Sn
Пример 2. Кластеризация методом K-средних
Отображение результатов кластеризации в ArcGis