Множественный регрессионный анализ

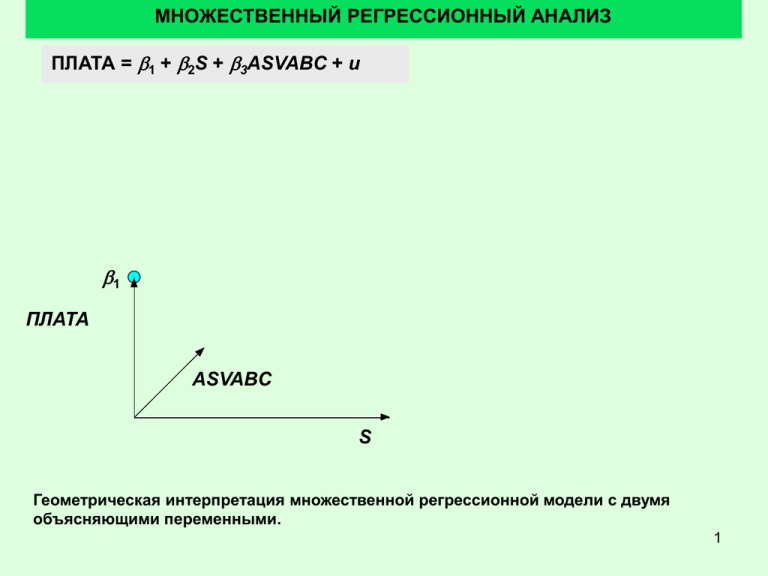
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
ПЛАТА = b1 + b2S + b3ASVABC + u
b1
ПЛАТА
ASVABC
S
Геометрическая интерпретация множественной регрессионной модели с двумя
объясняющими переменными.
1
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
ПЛАТА = b1 + b2S + b3ASVABC + u
b1
ПЛАТА
ASVABC
S
Смещение b1 буквально означает, какую плату получает респондент с нулевым
образованием и нулевым интеллектом. Поскольку мера интеллекта всегда отлична от
0, то значение функции никогда не будет равно смещению. Буквальная интерпретация
b1 - неуместна.
2
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
ПЛАТА = b1 + b2S + b3ASVABC + u
эффект образования S
b 1 + b 2S
b1
ПЛАТА
ASVABC
S
Вклад образования S. Один год учебы S увеличивает ПЛАТУ на b2 долларов, если
считать способности ASVABC постоянными.
3
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
ПЛАТА = b1 + b2S + b3ASVABC + u
b1 + b3ASVABC
эффект ASVABC
b1
ПЛАТА
ASVABC
S
Третий член дает вклад ASVABC. Увеличение ASVABC на 1 пункт увеличивает ПЛАТУ
на b3 $, если S постоянна.
4
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
ПЛАТА = b1 + b2S + b3ASVABC + u
b1 + b2S + b3ASVABC + u
u
b1 + b3ASVABC
Общий эффект S и
ASVABC
ASVABC эффект
S эффект
b1
b1 + b2S + b3ASVABC
b 1 + b 2S
ПЛАТА
ASVABC
S
Общий вклад обеих компонент. Это неслучайные компоненты. U –
случайное возмущение.
Вклад обеих компонент аддитивен и независим друг от друга. Что
оказывает большее влияние пока неизвестно.
5
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
Yi  b 1  b 2 X 2 i  b 3 X 3 i  ui
Yˆi  b1  b2 X 2 i  b3 X 3 i
ei  Yi  Yˆi  Yi  b1  b2 X 2 i  b3 X 3 i
Регрессионные коэффициенты вычисляются по принципу МНК. Оценка
Y в наблюдении i зависит от выбора b1, b2, и b3. Остатки ei в
наблюдении i есть разница между наблюдаемым и оцененным
значением Y.
6
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
RSS   ei2   (Yi  b1  b2 X 2 i  b3 X 3 i )2
  (Yi 2  b12  b22 X 22i  b32 X 32i  2b1Yi  2b2 X 2 iYi
 2b3 X 3 iYi  2b1b2 X 2 i  2b1b3 X 3 i  2b2 b3 X 2 i X 3 i )
  Yi 2  nb12  b22  X 22i  b32  X 32i  2b1  Yi
 2b2  X 2 iYi  2b3  X 3 iYi  2b1b2  X 2 i
 2b1b3  X 3 i  2b2 b3  X 2 i X 3 i
RSS
0
b1
RSS
0
b2
RSS
0
b3
Вычисление минимума RSS.
7
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
b1  Y  b2 X 2  b3 X 3
Cov( X 2 ,Y )Var( X 3 ) - Cov( X 3 ,Y )Cov( X 2 , X 3 )
b2 
2
Var( X 2 )Var(X 3 )  Cov( X 2 , X 3 )
Cov( X 3 ,Y )Var( X 2 ) - Cov( X 2 ,Y )Cov( X 2 , X 3 )
b3 
2
Var( X 2 )Var(X 3 )  Cov( X 2 , X 3 )
Значения коэффициентов для двух переменных. Зависимости для коэффициентов b
– более сложные, чем в простых регрессионных моделях.
8
СВОЙСТВА РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
Y  b1  b 2 X 2  b 3 X 3  u
Yˆ  b1  b2 X 2  b3 X 3
Cov( X 2 ,Y )Var( X 3 ) - Cov( X 3 ,Y )Cov( X 2 , X 3 )
b2 
2
Var( X 2 )Var(X 3 )  Cov( X 2 , X 3 )

1 Cov( X 2 ,[ b 1  b 2 X 2  b 3 X 3  u])Var( X 3 )
 

 - Cov( X 3 ,[ b 1  b 2 X 2  b 3 X 3  u])Cov( X 2 , X 3 )

1 [ b 2 Var( X 2 )  b 3Cov( X 2 , X 3 )  Cov( X 2 , u)])Var( X 3 )
 

 - [ b 2Cov( X 3 , X 2 )  b 3 Var( X 3 )  Cov( X 3 , u)]Cov( X 2 , X 3 )
Cov(X2, b1) = Cov(X3, b1) =0.
9
СВОЙСТВА РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
Y  b1  b 2 X 2  b 3 X 3  u
Yˆ  b1  b2 X 2  b3 X 3

1 [ b 2 Var( X 2 )  b 3Cov( X 2 , X 3 )  Cov( X 2 , u)])Var( X 3 )
b2  

 - [ b 2Cov( X 3 , X 2 )  b 3 Var( X 3 )  Cov( X 3 , u)]Cov( X 2 , X 3 )
 b 2 Var( X 2 )Var( X 3 ) - b 2 [Cov( X 3 , X 2 )]2

1

  b 3Cov( X 2 , X 3 )Var( X 3 ) - b 3 Var( X 3 )Cov( X 2 , X 3 )



Cov
(
X
,
u
)
Var
(
X
)

Cov
(
X
,
u
)
Cov
(
X
,
X
)
2
3
3
2
3


Cov( X 2 , u)Var( X 3 )  Cov( X 3 , u)Cov( X 2 , X 3 )
 b2 
Var( X 2 )Var( X 3 )  [Cov( X 2 , X 3 )]2
Отличие оценки от действительного значения b.
10
СВОЙСТВА РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
Y  b1  b 2 X 2  b 3 X 3  u
Yˆ  b1  b2 X 2  b3 X 3

1 [ b 2 Var( X 2 )  b 3Cov( X 2 , X 3 )  Cov( X 2 , u)])Var( X 3 )
b2  

 - [ b 2Cov( X 3 , X 2 )  b 3 Var( X 3 )  Cov( X 3 , u)]Cov( X 2 , X 3 )
 b 2 Var( X 2 )Var( X 3 ) - b 2 [Cov( X 3 , X 2 )]2

1

  b 3Cov( X 2 , X 3 )Var( X 3 ) - b 3 Var( X 3 )Cov( X 2 , X 3 )



Cov
(
X
,
u
)
Var
(
X
)

Cov
(
X
,
u
)
Cov
(
X
,
X
)
2
3
3
2
3


Cov( X 2 , u)Var( X 3 )  Cov( X 3 , u)Cov( X 2 , X 3 )
 b2 
Var( X 2 )Var( X 3 )  [Cov( X 2 , X 3 )]2
Коэффициенты при b3 сокращаются.
11
СВОЙСТВА РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
Y  b1  b 2 X 2  b 3 X 3  u
b2  b 2 
Yˆ  b1  b2 X 2  b3 X 3
Cov( X 2 , u)Var( X 3 )  Cov( X 3 , u)Cov( X 2 , X 3 )
Var( X 2 )Var( X 3 )  [Cov( X 2 , X 3 )]2
Var( X 3 )
Cov( X 2 , X 3 )
E (b2 )  b 2 
E Cov( X 2 , u)  
E Cov( X 3 , u) 


 b2
Несмещенность коэффициентов. Предположим X2 and X3 – неслучайные
переменные. Тогда E[Cov(X2, u)] and E[Cov(X3, u)] равны 0. То есть E(b2)
= b2 и b2 есть несмещенная оценка. То же и для b3.
12
СВОЙСТВА РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
Y  b1  b 2 X 2  b 3 X 3  u
Yˆ  b1  b2 X 2  b3 X 3
b1  Y  b2 X 2  b3 X 3
 ( b 1  b 2 X 2  b 3 X 3  u )  b2 X 2  b3 X 3
E (b1 )  b 1  b 2 X 2  b 3 X 3  E ( u )  X 2 E (b2 )  X 3 E (b3 )
 b1  b 2 X 2  b 3 X 3  X 2 b 2  X 3 b 3
 b1
b1 есть несмещенная оценка b1.
13
ТОЧНОСТЬ РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
Y  b1  b 2 X 2  b 3 X 3  u
Yˆ  b1  b2 X 2  b3 X 3
 u2
1
выборочная вариация b2   

nVar ( X 2 ) 1  rX22 , X 3
2
b2
Значения выборочных отклонений. Первый сомножитель идентичен простой
регрессии. Второй сомножитель есть функция коэффициента корреляции X1 и X2. Чем
больше корреляция, тем менее эффективна оценка, тем хуже уравнение объясняет Y.
14
ТОЧНОСТЬ РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
Y  b1  b 2 X 2  b 3 X 3  u
Yˆ  b1  b2 X 2  b3 X 3
 u2
1
 

nVar ( X 2 ) 1  rX22 , X 3
2
b2
стандартно е отклонение b2 
nk 2
E Var(e ) 
u
n
 u2
1

nVar ( X 2 ) 1  rX22 , X 3
n
s 
Var(e )
nk
2
u
2
u
s
1
s.e. (b2 ) 

2
nVar( X 2 ) 1  rX 2 , X 3
Вычисление стандартной ошибки. Чем выше корреляция, тем менее
15
эффективными являются значения коэффициентов регрессии.
ТОЧНОСТЬ РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
1
1
1
s.e.(b2 )  su 


n
Var( X 2 )
1  rX22 , X 3
n
n
1
s 
Var(e ) 
  (ei  e ) 2
nk
nk n
1
1
2

ei 
RSS

nk
nk
2
u
Оценка выборочного отклонения равна RSS, деленной на n-k.
16
ТОЧНОСТЬ РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ
• Доверительные интервалы коэффициентов
определяются так же, как и для простой
регрессии на основании t-теста
• Так же определяется состоятельность R2 на
основе F-критерия Фишера.
• Оценки МНК являются состоятельными
• Пример парной регрессии в Excel.
17