составить матрицу - Сделать заказ на решение

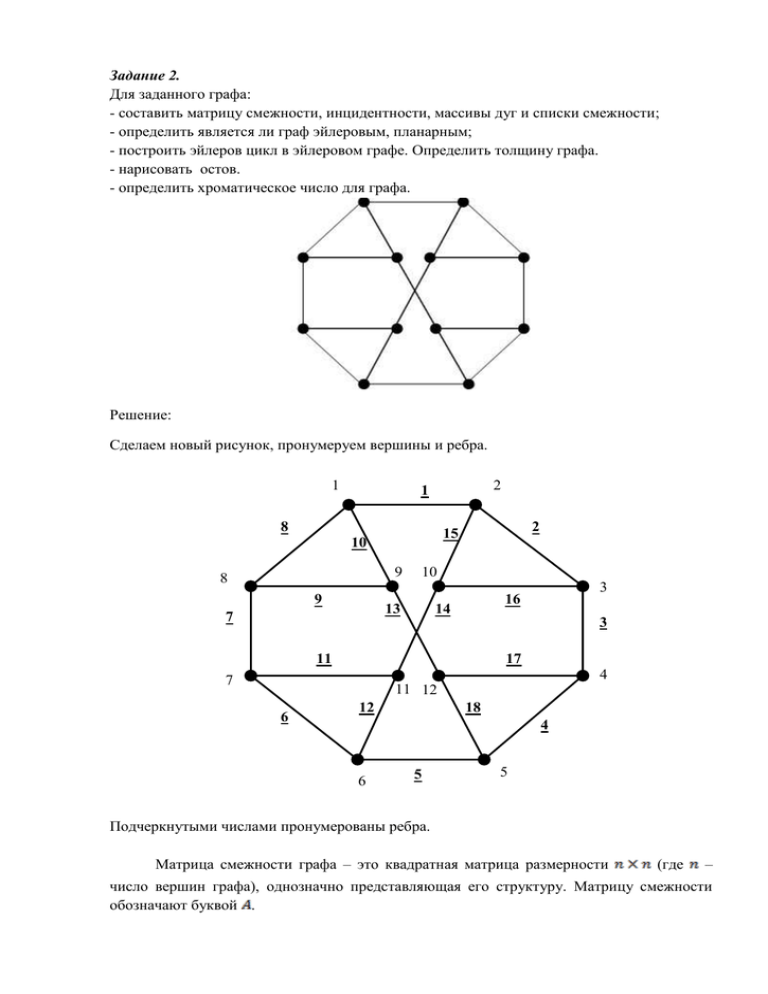
Задание 2.
Для заданного графа:
- составить матрицу смежности, инцидентности, массивы дуг и списки смежности;
- определить является ли граф эйлеровым, планарным;
- построить эйлеров цикл в эйлеровом графе. Определить толщину графа.
- нарисовать остов.
- определить хроматическое число для графа.
Решение:
Сделаем новый рисунок, пронумеруем вершины и ребра.
1
2
1
8
9
8
9
10
13
7
2
15
10
3
16
14
3
11
17
4
7
11 12
6
12
18
4
6
5
5
Подчеркнутыми числами пронумерованы ребра.
Матрица смежности графа – это квадратная матрица размерности
(где
–
число вершин графа), однозначно представляющая его структуру. Матрицу смежности
обозначают буквой .
, а каждый элемент матрицы определяется следующим образом:
, если существует ребро
, если нет ребра
,
Исходный граф имеет двенадцать вершин,
.
.
Запишем матрицу смежности
.
Матрица инцидентности представляет собой прямоугольную матрицу размером
, где – количество вершин графа, а
– количество ребер графа. Обозначается
матрица инцидентности
,
.
Каждый элемент матрицы определяется следующим образом
Запишем матрицу инцидентности:
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
1
Следующий тип задания графа - список дуг. Чаще всего это двумерный массив
размером 3*E (E-кол-во ребер), в первой строке которого хранится информация, из какой
вершины начинается дуга, во второй - в какой кончается, а в третьей строке - вес дуги. Т.к.
граф невзвешенный, то ограничимся двумя строками, но введем нулевую строку, в
которой запишем номера ребер.
номер
ребра
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 16 17 18
начало 1 2 3 4 5 6 7 8 8 9
7
6
9
11 10 10 12 12
конец 2 3 4 5 6 7 8 1 9 1
11 11 12 10 2
3 4 5
Так как граф неориентированный, то начало и конец можно поменять местами.
Список смежности содержит для каждой вершины графа список смежных ей вершин.
вершина 1
2
3
4
5
6
7
8
9
10
11
12
смежные 2,8,9 1,3,10 2,4,10 3,5,12 4,6,12 5,7,11 6,8,11 7,1,9 1,8,12 2,3,11 7,6,10 4,5,9
Граф, в котором существует эйлеров цикл, называется эйлеровым. Связный граф
является эйлеровым тогда и только тогда, когда степень каждой его вершины четная.
Проверим. Выпишем степени вершин:
Вершины нечетной степени – граф не является эйлеровым.
Граф называется планарным, если он изоморфен плоскому графу. Если его можно
изобразить на плоскости так, что никакие два ребра не будут иметь общих точек, кроме,
может быть, общего конца этих ребер.
Вершины 9 и 12 вынесем во внешнюю область и получим вот такой рисунок.
1
2
1
10
2
15
8
8
10
3
16
9
7
3
14
11
9
4
7
11
6
4
12
5
13
5
6
17
18
12
Никакие два ребра не имеют общих точек, кроме общего конца этих ребер.
Следовательно, граф является планарным.
Толщина графа— наименьшее число планарных частичных графов графа
объединение которых дает исходный граф
,
. Очевидно, что толщина планарного графа
равна 1.
Остов — дерево, содержащее все вершины графа и какие-то из его ребер. Если
неориентированный граф содержит вершин, то остов содержит
ребро. Любые две
вершины соединяет единственная простая цепь. Если какую-то пару несмежных вершин
соединить ребром, то полученный граф будет содержать ровно один цикл. Остов
определяется неоднозначно.
Для получения остова будем удалять ребра таким образом, чтобы разрушить циклы.
Исходный граф содержит
вершин, следовательно остов будет содержать
ребер.
Удалим ребра 2,4,6,8. Получим вот такую картинку.
1
2
1
15
10
9
8
9
10
13
7
16
14
3
3
11
17
4
7
11 12
12
18
5
6
5
Циклы все еще присутствуют. Поэтому удалим еще три ребра, например, 7, 3,5.
1
2
1
15
10
9
8
9
10
13
16
14
11
3
17
4
7
11 12
12
18
6
5
Полученный граф имеет 11 ребер и не имеет циклов. Получили один из остовов.
Хроматическое число графа G — минимальное число цветов, в которые можно
раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета.
Обозначается χ(G).
2
1
9
8
10
3
4
7
11 12
6
5
Раскрасим вершину один в первый цвет (отметим на рисунке крестиком). Далее
просматриваем по порядку вершины и раскрашиваем не раскрашенные несмежные с
первой вершины в этот же цвет. Такими вершинами будут 3,12, 7.
Раскрашиваем вершину 2 во второй цвет (отметим на рисунке смайлом), среди не
закрашенных вершин ищем несмежных со второй вершины и раскрашиваем их во второй
цвет. Такими вершинами будут 4, 11,8.
Аналогичным образом в третий цвет(треугольник) можно раскрасить вершины 9, 10,6.
Осталась одна вершина. Ни в один из предыдущих цветов ее раскрасить нельзя.
Раскрасим ее в цвет четыре.
Таким образом, хроматическое число графа