x=f(x)
advertisement
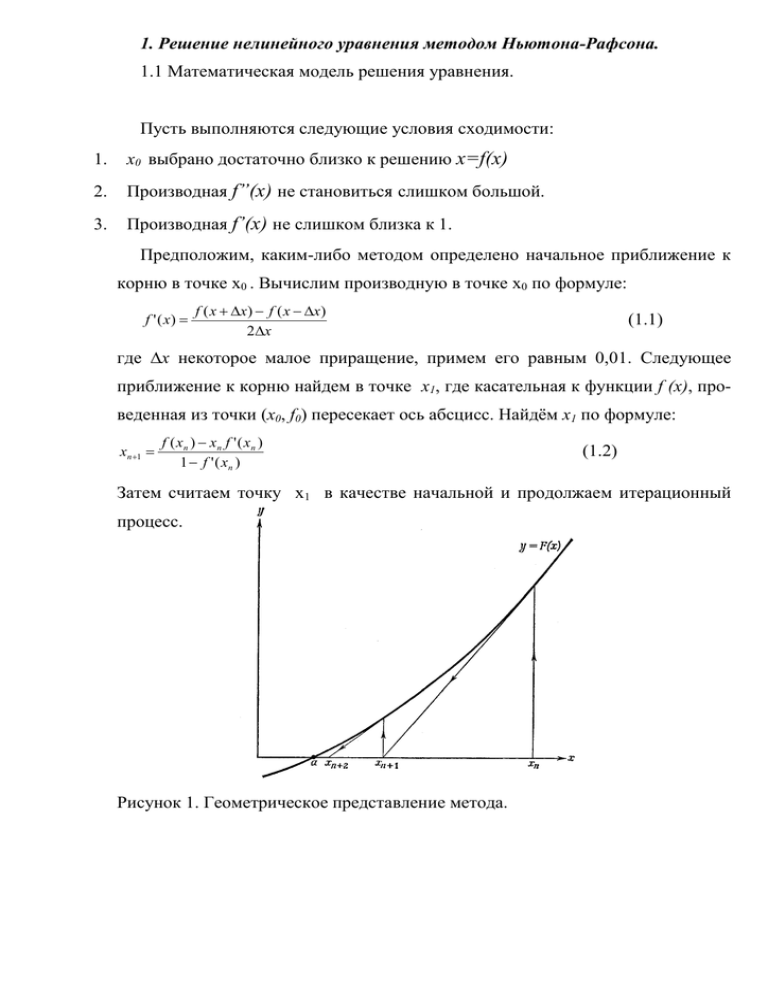
1. Решение нелинейного уравнения методом Ньютона-Рафсона. 1.1 Математическая модель решения уравнения. Пусть выполняются следующие условия сходимости: 1. x0 выбрано достаточно близко к решению x=f(x) 2. Производная f”(x) не становиться слишком большой. 3. Производная f’(x) не слишком близка к 1. Предположим, каким-либо методом определено начальное приближение к корню в точке x0 . Вычислим производную в точке x0 по формуле: f ' ( x) f ( x x) f ( x x) 2x (1.1) где ∆x некоторое малое приращение, примем его равным 0,01. Следующее приближение к корню найдем в точке x1, где касательная к функции f (x), проведенная из точки (x0, f0) пересекает ось абсцисс. Найдём x1 по формуле: xn 1 f ( xn ) xn f ' ( xn ) 1 f ' ( xn ) (1.2) Затем считаем точку х1 в качестве начальной и продолжаем итерационный процесс. Рисунок 1. Геометрическое представление метода. Из рисунка видно, что таким способом можно приближаться к корню a. При этом расстояние между очередным xn+1 и предыдущим xn приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие |xn+1 – xn| < (1.3) где - допустимая погрешность вычисления корня. 1.2 Решение уравнения. Данный метод был использован для нахождения корня в уравнении 2 x 2x 0 1 21 x (1.4) График функции f ( x) 2 x 2x 1 x 1 2 5 4.5 4 (1.5) Y 3.5 3 2.5 2 1.5 1 0.5 -5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 -0.5 -1 -1.5 -2 -2.5 -3 -3.5 -4 -4.5 -5 Рисунок 2. График функции. X 2 1.8 1.6 Y 1.4 1.2 1 0.8 0.6 0.4 0.2 X -2 -1.8-1.6-1.4-1.2 -1 -0.8-0.6-0.4-0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 -0.2 -0.4 -0.6 -0.8 -1 -1.2 -1.4 -1.6 -1.8 -2 Рисунок 3. График производной функции. Для нахождения корня уравнения (1.4) за значение начального приближения было взято значение x = -5. Корень был найден за 3 итерации c точностью 0.1. В программе Solver Microsoft Excel было найдено решение уравнения (1.4) за 3 итерации. График нахождения корня по итерациям: Таблица изменения x, f(x), f”(x) по итерациям 0 -1 -2 № ите- x рации -0.403 1 f(x) 2 0.033 -0.047 0.185 3 0 0 -0.477 0.016 -3 -4 -5 0 1 2 f’(x) 3 Нахождение к орня методом Ньютона Нахождение к орня методом Ньютона в Solver Microsoft Excel Корень уравнения 1.3 Оценка погрешности при нахождении корня уравнения (4): -0.034 Так, как ошибка не накапливается при использовании итерационных методов решения уравнений, то будем считать ошибку на последнем шаге итерационного процесса. Значит, ошибка будет содержаться при нахождении очередного приближения к корню по формуле (2). 1. Вычислим погрешность функции при x = 0: e = (1/(1-2))*0 - (20/(1-2)2)*(0.1+0.1) + 0 = 0.2 2. Вычислим погрешность производной функции при x = 0 и ∆x = 0.1: e = (1/(0.2))*(0.2+0.2) – (0/(0.2)2)*0 = 2 3. Вычислим итоговую погрешность при x = 0: e = 1*(0.2 + 0*2 - 0*0) – ((0 - 0*0)/12)*2 = 0.2 2. Решение системы нелинейных уравнений методом простой итерации. 2.1 Математическая модель решения уравнения. Пусть требуется решить систему уравнений f1 ( x1 , x2 , ... , xn ) 0 f ( x , x , ... , x ) 0 2 1 2 n f n ( x1 , x2 , ... , xn ) 0 (2.1) где f1, f2,…,fn – заданные нелинейные вещественнозначные функции n вещественных переменных x1, x2 …,xn. Введём обозначения: x1 x x 2 , x n f1 ( x ) f1 ( x1 , x2 ,, xn ) f 2 ( x ) f 2 ( x1 , x2 ,, xn ) F ( x) , f ( x ) f n ( x1 , x2 ,, xn ) n 0 0 0 . 0 Тогда систему (2.1) можно заменить одним уравнением F ( x) 0 (2.2) Для реализации метода простой итерации систему уравнений (2.1) преобразуем к следующему виду: x1 1 ( x1 , x2 , xn ) x ( x , x , x ) 2 2 1 2 n xn n ( x1 , x2 , xn ) (2.3) 1 ( x) x1 1 ( x1 , x2 , xn ) 2 ( x) x2 2 ( x1 , x2 , xn ) или в компактной записи: x ( x) . x ( x , x , x ) n n 1 2 n ( x ) n (2.4) На основании (2.4) запишем рекуррентное равенство: x ( k 1) (k ) ( x ) , (2.5) Где k определяет метод простых итераций. Запишем метод последовательных приближений (2.5) в развёрнутом виде: x1( k 1) 1 ( x1( k ) , x2( k ) , xn( k ) ) ( k 1) (k ) (k ) (k ) x2 2 ( x1 , x2 , xn ) x ( k 1) ( x ( k ) , x ( k ) , x ( k ) ) n 1 2 n n (2.6) Запишем «зейделеву» модификацию метода простых итераций: x1( k 1) 1 ( x1( k ) , x2( k ) , xn( k1) , xn( k ) ) ( k 1) ( k 1) (k ) (k ) (k ) x2 2 ( x1 , x2 , xn1 , xn ) ( k 1 ) ( k 1 ) ( k 1) ( k 1) ( k ) x n n ( x1 , x2 , xn1 xn ) (2.7) Согласно формуле (2.7) реализуем итерационный процесс. Для установления момента прекращения итераций при достижении заданной точности может быть использована метрика: || x ( k ) x || (2.9) 2.2 Решение системы уравнений. Решим данным методом систему уравнений: x12 3 x2 15 2 x1 x23 17 (2.10) Преобразуем систему (2.10) к виду (2.3): x1 15 3 x2 x2 3 17 x12 Реализуем итерационный процесс, возьмём за начальное приближение x1 = 1. В результате получим следующее значение x1 и x2 по итерациям: График изменения x1 и x2 по итерациям: Таблица изменения x1, x2, по Итерациям: 3.5 № ите- x1 x2 рации 1 3.464102 1.709976 3 2.5 2 3.141667 1.924694 3 3.037420 1.980993 4 3.009488 1.995237 5 3.002381 1.998809 6 3.000596 1.999702 7 3.000149 1.999926 2 1.5 1 2 3 4 5 6 7 Изменение x2 по итерациям Изменение x1 по итерациям x1 x2 3. Интегрирование функций. Пусть задан определённый интеграл: b F f ( x)dx (3.1) a Подынтегральная функция f(x) непрерывно дифференцируема на отрезке [a,b]. Тогда возможно вычисление определённого интеграла следующими методами: 3.1 Интегрирование функций методом правых и левых прямоугольников. Разделим отрезок [a,b] на N равных отрезков длиной ∆х, где x ba . N (3.2) Тогда координата правого конца i-го отрезка определяется по формуле x i = x0 + i∆х, (3.3) где x0 = a, i =0,1,…,N. y f(x) a b x b x Рисунок 3.1 Геометрическая интерпретация метода левых прямоугольников y f(x) a Рисунок 3.2 Геометрическая интерпретация метода правых прямоугольников Простейшая оценка площади под кривой f(x) может быть получена как сумма площадей прямоугольников, одна из сторон которого совпадает с отрезком [xi,xi+1], а высота равна значению функции в точке х, (метод левых прямоугольников, рисунок 3.1) или в точке xi+1 (метод правых прямоугольников, рисунок 3.2). Погрешность вычисления значения интеграла на каждом шаге показана на рисунках заштрихованными фигурами. Значение определенного интеграла вычисляется по формулам N 1 FL f ( xi )x (3.4) i 0 N FR f ( xi )x (3.5) i 1 для методов левых и правых прямоугольников, соответственно. 3.2 Интегрирование функций методом трапеций. Для вычисления значения интеграла разбиваем отрезок интегрирования [a,b]. на N равных частей и определим значения f (xi) (i = 0, 1, …, N), где xi = x0 + i∆х, x0 = a, i =0,1,…,N; x ba N y f(x) a b x Рисунок 3.3 Геометрическая интерпретация метода трапеций Используем линейную интерполяцию. В этом случае фигура, ограниченная графиком функции и прямыми х = хi , х = xi+1, является трапецией (Рисунок 3.3). Вычислим площадь Fi каждой из полученных трапеций: Fi x f ( xi 1 ) f ( xi ) . 2 (3.6) Искомый определенный интеграл определяется как сумма площадей всех трапеций: N 1 N 1 1 1 1 FN ( f ( xi 1 ) f ( xi )) x f ( x0 ) f ( xi ) f ( x N ) x . 2 i 0 2 i 1 2 (3.7) 3.3 Интегрирование функций методом Симпсона. Для вычисления значения интеграла разбиваем отрезок интегрирования [a,b] на N равных частей и определим значения f (xi) (i = 0, 1, …, N), где xi = x0 + i∆х, x0 = a, i = 0,1,…,N; x ba N Используем параболическую интерполяцию (полиномом второй степени) по трем соседним точкам: y = ax2 + bx + c. (3.8) Для нахождения коэффициентов а, b, с полинома, проходящего через точки (x0, y0), (x1, y1), (x2 ,y2), нужно найти решение следующей системы линейных уравнений: c (3.9) c c относительно неизвестных а, b, c. Решив систему (3.9) относительно неизвестных а, b, с любым известным методом (например, Крамера), подставив найденные выражения в (3.8) и выполнив элементарные преобразования, получаем: y y0 ( x x0 )( x x2 ) ( x x0 )( x x1 ) ( x x1 )( x x2 ) y1 y2 . ( x0 x1 )( x0 x2 ) ( x1 x2 )( x1 x2 ) ( x2 x0 )( x2 x1 ) (3.10) Площадь под параболой y = y(x) на интервале [хо, х2] находится посредством элементарного интегрирования (3.10): 1 F0 ( y0 4 y1 y 2 )x, 3 (3.11) где ∆х = x1 – x0 = x2 – x1. Искомый определенный интеграл находится как площадь всех параболических сегментов (формула Симпсона): FN 1 f ( x0 ) 4 f ( x1 ) 2 f ( x2 ) 4 f ( x3 ) ... 2 f ( x N 2 ) 4 f ( x N 1 ) f ( x N )x. (3.12) 3 3.4 Интегрирование функций методом Монте-Карло. Для вычисления значения интеграла представим, что подынтегральная функция лежит внутри прямоугольника высотой (d – c) и диной (b – a). Сгенерируем ЛГ пар случайных чисел, равномерно распределенных в данном прямоугольнике (рисунок 3.4): y a xi b, c yi dd (3.13) f(x) c a b рисунок 3.4 Пояснение метода Монте-Карло x Тогда доля точек (xi,yi), удовлетворяющих условию y ≤ f(xi), является оценкой отношения интеграла от функции f(x) к площади рассматриваемого прямоугольника. Следовательно, оценка интеграла в данном методе может быть получена по формуле: FN A ns N (3.14) где ns – число точек, удовлетворяющих условию yi ≤ f(xi), – полное количество точек, А — площадь прямоугольника. Можно предложить и другой путь вычисления определенного интеграла, рассматривая его как среднее значение функции f(x) на отрезке [a,b]: FN (b a ) 1 N f ( xi ), N i 1 (3.15) где xi – последовательность случайных чисел с равномерным законом распределения на отрезке [a,b]. 3.5 Уточнение найденного интеграла. Для вычисления интеграла с заданной точностью проверим условие |F2 - F1| . Если условие выполняется, то F2 принимается за искомое значение интеграла. Если условие не выполняется, то последнее значение интеграла F2 принимается за предыдущее, т. е. F1 = F2. После этого удвоим число точек деления отрезка (в методе Монте-Карло число случайно сгенерированных точек) и вычислим новое значение F2. Процесс удвоения N и вычисление F2 будем продолжать до тех пор, пока не выполнится условие |F2 - F1| . 3.6 Нахождение интеграла и оценка погрешности. Найдём значение интеграла 1 dx cos 0 2 x с точностью 0.001 и оценим погреш- ность вычисления интеграла. Для оценки погрешности вычислим значение интеграла по формуле Ньютона-Лейбница: b f ( x)dx F ( x) | b a F (b) F (a) (3.16) a 1 dx cos 2 0 x tg ( x) |10 tg (1) tg (0) tg (1) ≈1.5574077246 3.6.1Метод правых и левых прямоугольников. График нахождения интеграла по итерациям: Таблица изменения значения интеграла по итерациям: № ите- Значение интеграла Значение интеграла рации (метод левых пря- (метод правых моугольников) прямоугольников) 1.9 1.8 1.7 1.6 1.5 1.4 1.3 1 2 3 4 5 6 7 8 Метод левых прямоугольник ов Значение интеграла с точностью 10^-10 Метод правых прямоугольник ов 9 10 1 2 3 4 5 6 7 8 9 10 1.307879 1.419576 1.485075 1.520377 1.538675 1.547987 1.552684 1.555042 1.556224 1.556816 1.914259 1.722766 1.636670 1.596174 1.576574 1.566937 1.562159 1.559780 1.558593 1.558000 3.6.2 Метод трапеций. График нахождения интеграла по итерациям: 1.65 Таблица изменения значения интеграла по итерациям: № итерации Значение интеграла 1 1.562891 2 1.557871 3 1.557440 1.6 1.55 1.5 1.45 1 2 3 4 5 Значение интеграла с точностью 10^-10 Метод трапеций 3.6.3 Метод Симпсона. График нахождения интеграла по итерациям: Таблица изменения значения интеграла по итерациям: 1.57 1.565 1.56 1.555 1.55 1 1.5 2 2.5 Значение интеграла с точностью 10^-10 Метод Симпсона 3 № итерации Значение интеграла 1 1.611069 2 1.571171 3 1.560873 4 1.558276 5 1.557625 3.6.4 Метод Монте-Карло. График нахождения интеграла по итерациям: Таблица изменения значения интеграла по итерациям: № итерации Значение интеграла 1 0 2.4 2 1.6 1.2 0.8 0.4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Значение интеграла с точностью 10^-10 Метод Монте-Карло 3.6.5 Оценка погрешности методов нахождения интеграла. Для оценки погрешности методов возьмем за точное значение интеграла значение интеграла, вычисленное по формуле (3.16) с точностью 10-10. а) Метод левых прямоугольников: 1,5574077246 1,5568157690 = 0,0005919556 б) Метод правых прямоугольников: 1,5574077246 1,5580001043=0,0005923797 в) Метод трапеций: 1,5574077246 - 1,5576247707 = 0,0002170461 г) Метод Симпсона: 1,5574077246 - 1,5574399410 = 0,0000322164 д) Метод Монте-Карло: 1,5574077246-1,5571105927 = 0,0002971319 2 1.750000 3 1.312500 4 2.078125 5 1.531250 6 1.394531 7 1.462891 8 1.695313 9 1.476563 10 1.573975 11 1.553467 12 1.546204 13 1.536591 14 1.564682 15 1.541664 16 1.552559 17 1.559462 18 1.558040 19 1.556364 20 1.558959 21 1.557950 22 1.556861 23 1.558082 24 1.557111