разность векторов - Геометрия и математический анализ
advertisement
Настоящее пособие по выполнению контрольной работы по
геометрии (аналитическая геометрия на плоскости) для студентов заочного
отделения написано в соответствии с действующей программой и
предназначено для студентов-заочников физико-математического
факультета педагогического университета. В пособии дается необходимый
справочный материал, приводятся подробно разработанные типовые
примеры. Предлагаются задачи для самостоятельного решения. Варианты
контрольных работ приведены в таблице.
Контрольная работа выполняется в отдельной тетради в клеточку.
Записать номер и полную формулировку задачи. К задаче выполнить
рисунок, все пояснения к задаче писать подробно.
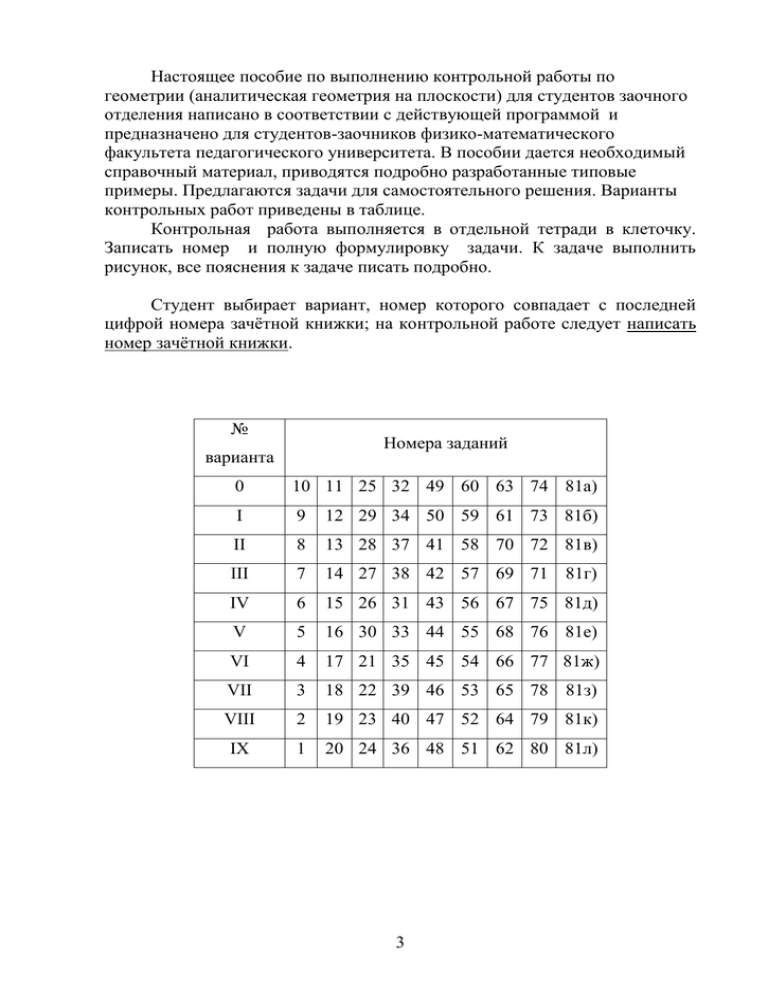
Студент выбирает вариант, номер которого совпадает с последней
цифрой номера зачётной книжки; на контрольной работе следует написать
номер зачётной книжки.
№
Номера заданий
варианта
0
10 11 25 32 49 60 63 74 81а)
I
9
12 29 34 50 59 61 73 81б)
II
8
13 28 37 41 58 70 72 81в)
III
7
14 27 38 42 57 69 71 81г)
IV
6
15 26 31 43 56 67 75 81д)
V
5
16 30 33 44 55 68 76 81е)
VI
4
17 21 35 45 54 66 77 81ж)
VII
3
18 22 39 46 53 65 78 81з)
VIII
2
19 23 40 47 52 64 79 81к)
IX
1
20 24 36 48 51 62 80 81л)
3
BAРИАНТ КОНТРОЛЬНОЙ РАБОТЫ С РЕШЕНИЕМ
Элементы векторной алгебры
Задача № 1.
Векторы АC m , BD n служат
диагоналями
параллелограмма ABCD. Выразить векторы АВ , ВС , СD , DА через вектора
m и n.
Решение.
По определению суммы и разности
векторов имеем: ВС + СD = n и
А
В
n
m
ВС – СD = m . Сложим эти равенства
ВС + СD + ВС – СD = n + m , получим:
m n
ВС
.
2
С
D
m n n m
Далее, вектор СD = BD ВС , СD = n –
=
.
2
2
Так как ABCD параллелограмм (по условию), то векторы АВ и СD ,
векторы ВС и DА противоположно направлены, следовательно,
n m m n
m n
; DА
.
АВ = СD , DА ВС , тогда АВ =
2
2
2
Так как ABCD параллелограмм (по условию), то векторы АВ и СD ,
векторы ВС и DА противоположно направлены, следовательно,
n m m n
m n
; BC
.
АВ = СD , DА ВС , тогда С D =
2
2
2
n m m n
m n
n m m n
m n
Ответ: АВ =
; DА
; СD =
; BC
.
2
2
2
2
2
2
Задача № 2. В базисе e1 , e 2 , e3 даны векторы: p - 3,6,-13 , a 1,0,2
b 1,-1,3 и c-2,3,0 . Представить вектор p как линейную комбинацию
векторов a, b , c .
p как линейную комбинацию
Решение. Представить вектор
векторов a, b , c . Т.е. вектор p разложить по векторам a, b , c :
p α a β b γ c (*) .
Наша задача – найти коэффициенты разложения , , .
4
Векторы a, b , c , p разложим по векторам базиса e1 , e 2 , e3 , т.е.
Представим эти векторы в виде:
a e1 - 2e3 , b e1 - e2 3e3 , c -2e1 3e2 , p -3e1 6e2 - 13e3 .
В равенстве (*) подставим вместо векторов a, b , c , p их разложения по
векторам базиса:
- 3e1 6e2 -13e3 α(e1-2e3 ) β(e1-e2 3e3 ) γ(- 2e1 3e2 ) .
Преобразуем:
-3e1 6e2 -13e3 αe1-2αe3 βe1-βe2 3 βe3 -2γe1 3γe2 ,
o (α β-2γ 3 )e1 (-β 3γ-6 )e2 (- 2α 3 β 13 )e3 .
0
0 e1 0 e2 0 e3 , поэтому в силу единственности разложения
Но
вектора по векторам базиса можно записать следующую систему:
α β-2γ 3 0
-β 3γ-6 0
-2α 3 β 13 0
Решая эту систему относительно , , , получим: α 2 , β -3, γ 1 .
Подставим эти значения в равенство (*).
p 2a-3b c – искомая линейная комбинация.
Ответ: p 2a-3b c .
Задача № 3. Даны три ненулевых вектора а , b , с , каждые два из
которых неколлинеарны. Найти их сумму, если вектор а + b коллинеарен
вектору с , а вектор b + с коллинеарен вектору а .
Решение.
коллинеарен вектору а ,
тогда
имеем в силу условия коллинеарности
векторов: а + b с и b + с а .
Найдем сумму векторов а , b , с :
а + b + с ( 1) с и а + b + с ( 1) а .
В итоге имеем ( 1) с ( 1) а . Поскольку векторы а и с
неколлинеарны (по условию), последнее равенство возможно, если
1 , т.е. а + b + с = 0 .
По условию а + b коллинеарен вектору с , а вектор b + с
Ответ: а + b + с = 0 .
5
Задача № 4. Найти длину вектора с 3 a 4 b , если а = 2, b = 3,
^
a, b .
3
2
Решение. По свойству скалярного произведения с = с , распишем
скалярный квадрат вектора c , с учётом того , что с 3 a 4 b :
2
2
2
2
с = с = (3 a 4 b ) 9 a 24 a b 16 b .
Далее,
2
2
2
зная, что а = а ;
b
= b
2
и
а b = а · b сos ( а , b )
подставим их значения в полученную формулу:
2
2
2
2
с 9 a 24 a b 16 b 9 а 24 а b cos 16 b
3
1
9 4 24 2 3 16 9 108 6 3 .
2
Ответ: с 6 3
Метод координат на плоскости
Задача № 5. Даны координаты вершин треугольника АВС: А(4, 1),
В(7, 5), С(-4, 7). Вычислить длину биссектрисы AD
А
угла А.
Решение. Точка D – основание биссектрисы делит
отрезок ВС в некотором отношении λ=BD:DC. По
свойству биссектрисы внутреннего угла треугольника
имеем: BD:DC=AB:AC.
Найдем длины сторон АВ и АС
( как расстояния между двумя данными точками):
В
D
С
AB AB (7 4) 2 (5 1) 2 5, AC AC (4 4) 2 (7 1) 2 10 .
Получим AB:AC = 5:10 =0,5.
Таким образом, λ=0,5. Координаты точки D найдем, используя
x B λxC
y λyC
, yD B
формулы: x D
, где (x D ,y D ), (x B ,y B ), (x C ,yC ) 1 λ
1 λ
координаты точек D, B и C соответственно.
Подставляя известные данные, получим:
10 17
7 0,5 ( 4 ) 10
5 0,5 7 17
x
, y
. Значит, D ( , ) .
D
D
1 0,5
3
1 0,5
3
3 3
Найдем длину отрезка AD:
6
2
2
200 10 2
10
17
AD AD 4 1
.
9
3
3
3
Ответ: AD
10 2
.
3
Задача № 6. Относительно репера R (O, e1 , e2 ) даны координаты
точек: О΄(2,-3), А΄(1,1), В΄(3,-6), М(5,-1). Найти координаты точки М в
репере R (O, A, B) .
Решение. Обозначим координаты точки М относительно репера R΄ за
x΄ и y΄. Пусть e1 OA, e2 OB , тогда e1 1,4, e2 1,3.
Запишем формулы преобразования общей декартовой системы
координат для нашего случая:
x = -x΄+y΄+2
y = 4x΄-3y΄-3 ,
где ( x΄, y΄) – координаты точки в новом репере,
(x , y) – координаты точки в старом репере. Для точки М имеем x=5,
y=–1. Получаем:
-x΄+y΄+2=5
4x΄-3y΄-3=-1.
Решая эту систему относительно x΄ и y΄, получим x΄=11, y΄=14.
Таким образом, М (11,14)R΄.
Ответ: М (11,14) в репере R (O,A,B ) .
Прямая на плоскости
Задача № 7. Составить уравнение прямой, проходящей через точку
М(1,5)
и наклоненной к прямой x-y+3=0 под углом, тангенс которого
3
равен .
5
Решение. Пусть ℓ – данная прямая, ℓ1 – искомая прямая, k и k1 –
угловые коэффициенты прямых ℓ и ℓ1 соответственно. Уравнение прямой ℓ
можно переписать в виде: y=x+3 (уравнение с угловым коэффициентом).
Таким образом, k=1.
Тангенс угла α между прямыми ℓ и ℓ1 находят по формуле:
k k
tg 1
.
1 k1k
7
3
Используя эту формулу и данные задачи ( tg ), запишем:
5
k1 k 3
. Решая это уравнение, получим k1=4.
1 k1k 5
Уравнение прямой ℓ1 можно записать в виде: y=4x+b. Точка М
принадлежит прямой ℓ1, поэтому координаты точки удовлетворяют
уравнению прямой ℓ1: 5=4·(-1)+b. Отсюда находим: b=9. Поэтому ℓ1:
y=4x+9.
Ответ: ℓ1: y=4x+9.
Задача № 8. Составить уравнения сторон треугольника АВС, зная
одну из его вершин А(3,0) и уравнения двух медиан 7x-5y+15=0, 4x+y+6=0.
Решение. Пусть СК и BD – медианы ∆АВС, и пусть СК: 7x-5y+15=0,
BD: 4x+y+6=0. СК пересекает BD в точке О (см. рис.), поэтому координаты
точки О удовлетворяют уравнениям медиан. Найдем
B
координаты точки, решив систему:
7x-5y+15=0
К
O М
4x+y+6=0
A
5
2
5 2
D
Получим x= , y= . Таким образом О( ; ).
C
3 3
3
3
Точка О делит отрезок АМ в отношении λ=2:1 (свойство точки
пересечения медиан треугольника).
Используя формулы для нахождения координат точки, делящей
данный отрезок в данном отношении, запишем:
5 3 2 xM
,
3
1 2
2 0 2 yM
.
3
1 2
Отсюда найдем координаты точки М: xM=-4, yM=1.
Далее найдем координаты точек В и С, используя следующие условия:
точка М является серединой отрезка ВС, координаты точки В
удовлетворяют уравнению медианы BD.
Координаты точки С удовлетворяют уравнению медианы СК.
Таким образом, получим четыре уравнения, которые рассмотрим в
системе:
x B xC
4
2
y B yC
1
2
4 xB y B 6 0
7 xC 5 yC 15 0
Решая систему, получим: В(-3, 6), С(-5,-4).
8
Используя формулу для нахождения уравнения прямой, проходящей
через две точки, запишем уравнение сторон ∆АВС.
x3 y6
AB :
x y - 3 0,
33 06
x5 y4
AC :
x - 2y - 3 0,
35 04
x5
y4
BC :
5x - y 21 0.
-35 64
Ответ: x+y-3=0, x-2y-3=0, 5x-y+21=0.
Задача № 9. Составить уравнение биссектрисы того угла между
прямыми 2x-y+7=0 и 3x-6y-8=0, в котором лежит точка М(1,2).
Решение. Пусть А(x, y) – точка биссектрисы угла между данными
прямыми ℓ1 и ℓ2 (см. рис.). Используя формулу для нахождения расстояния
от данной точки до данной прямой, выразим:
2x y 7
М
расстояние от А до ℓ1: 1
,
l1
5
А
3x 6 y 8
l2
расстояние от А до ℓ2: 2
.
3 5
По свойству точек биссектрисы угла имеем: 1 2 , т.е.
2x y 7
5
3x 6 y 8
3 5
, 3 2x - y 7 3x 6 y 8 (*) .
Составим систему неравенств, определяющую полуплоскость угла, в
которой лежит точка М(1,2). Для этого подставим координаты точки М в
трехчлены: 2x-y+7 и 3x-6y-8, и выясним знак каждого трехчлена.
2∙1-2+7>0 2x-y+7>0 (1)
3∙1-6∙2-8<0 3x-6y-8<0 (2)
С учетом равенств (1) и (2), которые нужно рассматривать в системе,
раскроем модули в равенстве (*): 3(2x-y+7)=–(3x-6y-8).
Преобразуя, получим уравнение биссектрисы: 9x-9y+13=0.
Ответ: 9x-9y+13=0.
Геометрические преобразования
Задача № 10. На биссектрисе внешнего угла С треугольника АВС
взята точка М, доказать, что АС+СВ<АМ+МВ.
9
Доказательство. Пусть (см. рис.), ВСК – внешний угол ∆АВС
(см. рис.), обозначим ВСК=. М – произвольно взятая точка на
биссектрисе угла .
Рассмотрим поворот плоскости вокруг точки С на угол - (угол
отрицательный, т.к. вращение по часовой стрелке): RC-.
RC-: ВВ1, В1СК. Проведем ВВ1, ВС=В1С (по определению
поворота) ∆ВСВ1 – равнобедренный.
Значит, СО – высота и медиана ∆ВСВ1.
Рассмотрим ∆ВМВ1. ОМ - высота и медиана ∆ВМВ1, значит ∆ВМВ1 –
равнобедренный. Поэтому ВМ=В1М.
Итак,
ВМ=В1М
и
ВС=В1С.
Рассмотрим
∆АМВ1:
АВ1<АМ+МВ1
АС+СВ1<АМ+МВ
АС+СВ<АМ+МВ.
Что и требовалось
доказать.
В
М
О
А
С
В1
К
Задача № 11. Где следует построить мост через реку, разделяющую
пункты А и В, чтобы путь l AP PQ QB был кратчайшим. Берега реки
считаются параллельными прямыми a
и b, а мост строится
перпендикулярно берегам реки.
Решение. Длина отрезка PQ не зависит от положения точки Р на
прямой а, а вектор а PQ
определяется
прямыми a и b . Поэтому
надо найти такое положение
точки Р, чтобы сумма
AP PQ была наименьшей.
Пока отрезки AP и QB удалены
друг от друга.
А
а
P
а
b
Q
B
10
Переведем отрезок AP в положение AQ
параллельным
переносом на
а
вектор . Получим ломаную
P
а
линию AQВ . Длина ломаной,
A
а значит, длина l, будет
а
наименьшей в том случае, когда
Q
b
точки A, Q, В лежат
на одной прямой.
B
Итак, Q – точка пересечения отрезка AВ с прямой b, а точка Р –
проекция Q на прямую а.
А
Кривые второго порядка
Задача № 12. Составить уравнение эллипса, если прямые x
8
3
служат директрисами эллипса, а малая полуось равна 2.
Решение. Общее уравнение эллипса:
x2 y2
1. По условию b=2.
a2 b2
Найдем большую полуось а.
Известно, что уравнение директрис эллипса имеет вид: x
где – эксцентриситет эллипса,
запишем: x
a2
c
Решая
Таким
(1) ,
(3) .
(4). С учетом (3), (4) и
8
4c
8
) запишем:
3c 2 8c 4 3 0 .
c
3
3
уравнение, получим c1 2 , c 2 2 3 a 12 16 3 , a 22 16 .
3
образом,
2
можно
составить
удовлетворяющих данным условиям:
Ответ:
c
(2) , с2=a2-b2. С учетом (1) и (2)
a
Но a2=b2+с2, в нашем случае a2=4+с2
условия ( x
a
2
уравнения
2
2
двух
2
x
y
x
y
1,
1.
16
4
16 4
3
x2
y2
x2 y2
1,
1.
16
4
16 4
3
11
эллипсов,
Задача № 13. Привести к каноническому виду данное уравнение и
построить соответствующую линию: 9x2+4xy+6y2+2x-4y-4=0.
Решение. Чтобы решить задачу, необходимо рассмотреть несколько
этапов.
Сначала определим коэффициенты:
а11=9, а22=6, а12=2, а10=1, а20=-2, а00=-4.
1) 2-15+50=0, 1=10, 2=5.
1
1
2
, cos
2) tg , sin
.
2
5
5
2 1
1 2
i
i
j , j i
j
5
5
5
5
2
1
1
2
x
x
y , y
x
y (1) .
5
5
5
5
5 , а22
5,
3) а11 10, a10 0, а12 0, a20
10x 2 5 y 2 2 5 y 4 0 .
2 5
y ) 4 0
5
2
1
1 2
10x 2 5( y 2
y ) 4 1 0 , 10x 2 5( y
) 5 0 ,
5
5
5
4) 10x 2 5( y 2
x x, y y -
1
(2) ,
5
10x 2 5 y 2 5 ,
1
) в репере R (O, i , j ) .
5
Уравнение
(*) – каноническое
R (O, i , j ) .
5) см. рисунок.
2x 2 y 2 1 (*)
O(0,
уравнение эллипса в репере
y
y/=y//
x//
1
x/
O/
x
O
12
1
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
1. На плоскости даны два вектора p { 2, 3 } и q { 1, 2 } . Найти
разложение вектора а {9, 6} по базису p и q .
2. Даны три вектора а { 3, 1 }, b { 1, 2 } и c {-1, 6 } . Найти разложение
вектора p a b c по базису а, b .
3. Даны три вектора p{ 3, -2, 1 } , q {-1, 1, -2 } и r { 2, 1, -3 } . Найти
разложение вектора c { 9, -6, 5 } по базису p , q, r .
4. Даны векторы l 2а b c , m 2b - c - а , n 2c a b . Векторы
a , b и c – некомпланарны. Проверить, будут ли компланарны векторы
l , m и n . В случае утвердительного ответа дать линейную зависимость, их
связывающую.
5. Даны векторы a r , b p - q - r , c p - q r . Векторы p ,q ,r –
некомпланарны. Выяснить, будут ли компланарны векторы а , b и c . В
случае утвердительного ответа дать линейную зависимость, их
связывающую.
6. Даны четыре вектора: a {2,1,0}, b {1, - 1, 2}, c {2, 2, - 1} и d (3, 6, - 6) .
Найти разложение вектора d по векторам a , b и c .
7. Дано разложение вектора с по базису i , j , k : c 16 i 15 j 12 k .
Определить разложение по этому же базису вектора d , параллельного
вектору с и противоположного с ним направления, при условии, что
d = 75.
8. На плоскости даны четыре точки А(1; 2) , В(2; 1) , С (3; 2) и
D (2; 3) . Определить разложение векторов
АD , ВD , CD и АD + ВD + CD ,
принимая в качестве базиса векторы АВ и АС .
9. Пусть р1 и
р 2 – произвольные векторы. Доказать, что векторы
+ р 2 , b р1 –2 р 2 , с – р1 –4 р 2
коэффициенты линейной зависимости.
а р1
линейно
зависимы.
Найти
10. Даны неколлинеарные векторы а , b . Доказать, что система
векторов m 3 a b , n 2 a b , p a 3 b линейно зависимая, векторы n , р не
коллинеарны. Разложить вектор m по векторам n , р .
13
11. Векторы a и b образуют угол 6 ; зная, что a 3, b 1 ,
найти угол между векторами p a b и q a - b .
12. Найти тупой угол, образованный медианами, проведёнными из
вершин острых углов равнобедренного прямоугольного треугольника.
s и t , если известно,
13. Какой угол образуют единичные
векторы
что векторы p s 2t и q 5s -4t взаимно перпендикулярны.
14. Зная, что a 2, b 5 и (a^ b ) 2 3 . Найти, при каком значении
векторы p a 17b и q 3a b окажутся перпендикулярными.
15. Зная векторы a и b , на которых построен параллелограмм,
выразить через них вектор, совпадающий с высотой параллелограмма,
перпендикулярный к стороне a .
16. Найти длину диагоналей параллелограмма, построенного на
векторах a 5 p 2q и b p 3q , если p 2 2, q 3 и ( p^q ) 4 .
^
17. Известно, что а =3, b = 4; a , b 120o . Вычислить:
скалярное произведение векторов 2 a b и 3 a b и 3 a b .
18. Вычислить угол, который образуют единичные векторы а и b ,
если известно, что векторы m 3 a b , n 2 a 2 b взаимно перпендикулярны.
19. Треугольник АВС задан векторами АВ 1; 0; 2 и АС 3; 1; 2.
Найдите длины медиан АМ и ВР треугольника и угол между ними.
20. Векторы а , b и с попарно образуют друг с другом углы, каждый
из которых равен 60 o . Зная, что а =4, b = 2, с = 6, определить модуль
вектора р а + b + с .
21. Даны вершины треугольника А(2, –5), В(1, –2), С(4, 7). Найти
координаты точки пересечения со стороной АС биссектрисы его
внутреннего угла при вершине В.
22. Даны вершины треугольника А(–1, –1), В(3, 5), С(–4, 1). Найти
длину биссектрисы его внутреннего угла при вершине А.
23. Даны вершины треугольника А(1, 4), В(3, –9), С(–5, 2). Найти
длину высоты, проведенной из вершины В.
24. Отрезок АВ разделён точками P(2, 2) и Q(1, 5) на три равные
части. Найти координаты точек А и В и длину отрезка АВ.
25. Прямая проходит через точки А(7, –3) и В(23, –6). Найти точку
пересечения этой прямой с осью абсцисс и длину отрезка АВ.
26. Найти координаты точки, равноудалённой от трёх данных точек
А(2, 2), В(5, 1) и С(7, –3).
27. Даны вершины четырёхугольника А(-2, 2), В(1,6), С(8,1) и D(0,-3).
Найти, в каком отношении его диагональ АС делит диагональ BD.
14
28. Точки М(1, 6), N(–4,2), Р(3,–2) – середины сторон треугольника.
Найти координаты его вершин.
29. Даны вершины параллелограмма ABCD: А(4,5; 5), В(2; –6) и точка
пересечения его диагоналей М(3; 1,5). Найти координаты остальных
вершин параллелограмма.
30. Даны вершины треугольника АВС: А(3, 6), В(–3,5). Определить
координаты точки С, если известно, что середины сторон АС и ВС лежат на
осях абсцисс и ординат.
31. Найти координаты точки, имеющей одни и те же координаты в
системах { O e1e2 } и { O e1e2 } , где O( 2,3 ), e1{1, 3 }, e2 { 2, 1} .
32. В системе { O e1e2 } точки А и В имеют координаты (1, 1) и (2, 2).
Существует ли такая новая система координат, начало которой совпадает с
началом старой системы и в которой точки А и В имеют координаты (1, 1)
и (–1, –2)?
33. В треугольнике ОАВ: OA e1 , OB e2 . Записать формулы перехода
от данной системы координат к системе координат, у которой
O B , e1 AB, e2 AO .
34. Определить старые координаты нового начала ПДСК и угол , на
который повёрнуты оси, если формулы преобразования координат имеют
2
2
x
x
y 5
2
2
вид:
. Записать уравнение линии x+2y–1=0 в
2
2
y
x
y 3
2
2
новой системе координат.
35. В системе { O e1e2 } прямая задана уравнением: x–2y+1=0. Найти
уравнение этой прямой в системе { O e1e2 } , если O( 1, 0 ), e1{ 1, 3 }, e2 { 4, 4} .
36. Найти формулы преобразования ПДСК, если i
1 2
i
j,
5
5
O ( 2 ,12 ) и системы имеют различную ориентацию.
37. А(2, 1), В(–3/2, 3). Существует ли новая система координат с
началом в точке (0, 1), в которой точка А имела бы координаты (1, 0),а
точка В имела бы координаты (0, 1)?
38. В треугольнике ОАВ проведены медианы AD и ВК
пересекающиеся в точке О/ . Написать
формулы преобразования
координат при переходе от системы координат О , OA e1 , OB e2 к системе
координат O , e1 О / A, e2 O / B .
39. Найти формулы преобразования ПДСК, если i
O ( 3, 2 ) и системы имеют одну и ту же ориентацию.
15
2 7 2
i
j,
10
10
40. В треугольнике ОАВ: OA e1 , OB e2 . Записать формулы перехода
от данной системы координат к системе координат, у которой
O А, e1 AB, e2 AO .
41. Найти точку Q, симметричную точке Р(–1, 5) относительно
прямой x-2y-3=0.
42. Найти точку М симметричную точке N(8,–9) относительно
прямой, проходящей через точки А(3, –4) и В(–1, –2).
43. На прямой x-2y-5=0 найти точку, сумма расстояний которой до
точек А(–7, 1) и В(–5, 5) была бы наименьшей.
44. Даны вершины треугольника: А(–10, –13), В(–2, 3), С(2, 1). Найти
длину перпендикуляра, опущенного из вершины В на медиану,
проведенную из вершины С.
45. Составить уравнение прямой, проходящей через точку Р(–2, 3) на
одинаковых расстояниях от точек А(5, –10) и В(3, 7).
46. Составить уравнение прямой, которая проходит через точку
пересечения прямых 2x+y-2=0, x-5y-23=0 и делит пополам отрезок,
ограниченный точками М1(5, –6) и М2(–1, –4).
47. Даны вершины треугольника: А(2, –2), В(3,–5), С(5, 7). Составить
уравнение перпендикуляра, опущенного из вершины С на биссектрису
внутреннего угла при вершине А.
48. Дана прямая 2x+3y+4=0. Составить уравнение прямой,
проходящей через точку В(2, 1) под углом 450 к данной прямой.
49. Найти точку М симметричную точке N(2,–4) относительно
прямой, проходящей через точки А(–1,5) и В(11, –1).
50. Через точку N(–1,4) проведена прямая, расстояние которой до
точки Q(–2,–1) равно 5. Составить её уравнение.
51. Составить уравнения сторон треугольника, зная одну его вершину
В(1,–6), а также уравнения высоты 2x+y+9=0 и медианы x+3y+5=0,
проведенных из различных вершин.
52. Составить уравнения сторон треугольника, зная одну его вершину
А(3, –1), а также уравнение биссектрисы x-4y+10=0 и медианы 6x+10y-59=0,
проведенных из различных вершин.
53. Даны уравнения двух сторон квадрата 4x-3y+3=0, 4x-3y-17=0 и
одна из его вершин А(2, –3). Составить уравнения двух других сторон этого
квадрата.
54. Даны уравнения двух сторон прямоугольника 3x-2y-10=0,
2x+3y+3=0 и одна из его вершин А(–2, 3). Найти площадь прямоугольника.
55. Составить уравнения сторон треугольника, зная одну его вершину
В(2,7), а также уравнения высоты 3x+y+11=0 и медианы x+2y+7=0,
проведенных из одной вершины.
16
56. Составить уравнения сторон треугольника, зная одну его вершину
В(5,4), а также уравнения высоты 8x+y–9=0 и биссектрисы 2x–y–1=0,
проведенных из различных вершин.
57. Составить уравнения сторон треугольника, зная одну его вершину
С(–5,3), а также уравнения биссектрисы 2x–y+5=0 и медианы 4x–y+7=0,
проведенных из одной вершины.
58. Составить уравнения сторон треугольника, зная одну его вершину
С(4,–1), а также уравнения двух биссектрис x–1=0 и медианы x–y–1=0.
59. Даны уравнения двух сторон прямоугольника 5х+2у–7=0,
5х+2у–36=0 и уравнение его диагонали 3х+7у–10=0. Составить уравнения
остальных сторон и второй диагонали этого прямоугольника.
60. Точка Е(1,–1) является центром квадрата, одна из сторон
которого лежит на прямой x–2y+12=0. Составить уравнения прямых, на
которых лежат остальные стороны этого квадрата.
61. Точка В лежит на отрезке АС (АВ≠ВС). На АВ и ВС, в одной
полуплоскости, построены равносторонние треугольники АВЕ и ВСF.
Точки М и N середины АF и ЕС соответственно. Доказать, что треугольник
ВМN правильный.
62. Даны две равные окружности и на каждой из них соответственно
точки M и N. Построить центр поворота, отражающего одну окружность на
другую, чтобы при этом точка M перешла в точку N.
63. Два равносторонних треугольника АВС и АВ1С1 ориентированы
одинаково. Найти угол между прямыми ВВ1 и СС1. Доказать, что ВВ1=СС1.
64. Окружность пересекает две концентрические окружности. Одну в
точках А и В, вторую в точках С и D. Доказать, что хорды АВ и СD
параллельны, АС=ВD, АD=ВС.
65. В трапеции ABCD отношение оснований AD:BC=5:2; O – точка
пересечения диагоналей. Найти отношения площади трапеции к площади
треугольника ADO.
66. Точки А и В лежат по одну сторону от прямой а. На прямой а
найти точку С, чтобы периметр треугольника АВС был наименьшим.
67. На сторонах АВ и АС треугольника АВС вне его построены
квадраты ABDE и ACFM. Докажите, что а) отрезки ЕС и ВМ равны и
взаимно перпендикулярны; б) медиана АР треугольника АВС
перпендикулярна отрезку ЕМ и равна его половине.
68. Доказать, что композиция трех центральных симметрий с
центрами А,В,С есть центральная симметрия с центром D, причем АВ DC .
69. На сторонах АВ и АС треугольника АВС, вне его построены
квадраты ABDE и ACFM. Докажите, что а) отрезки ЕС и ВМ равны и
взаимно перпендикулярны;
70. На сторонах АВ и АС треугольника АВС, вне его построены
квадраты ABDE и ACFM. Докажите, что медиана АР треугольника АВС
перпендикулярна отрезку ЕМ и равна его половине.
17
71. Составить уравнение эллипса, фокусы которого лежат на оси
абсцисс симметрично относительно начала координат, если его малая ось
равна 6, а расстояние между директрисами равно 13.
72. Составить уравнение эллипса, фокусы которого лежат на оси
ординат симметрично относительно начала координат, если расстояние
12
между фокусами 24, а эксцентриситет равен
.
13
73. Составить уравнение гиперболы, фокусы которой расположены на
оси абсцисс симметрично относительно начала координат, если она имеет
4
3
асимптоты y x и расстояние между фокусами равно 20.
74. Составить уравнение гиперболы, фокусы которой расположены на
оси абсцисс симметрично относительно начала координат, если расстояние
8
3
между директрисами равно и эксцентриситет равен .
3
2
75. Найти точки гиперболы
x2 y2
1 , расстояние от которых до
9 16
левого фокуса равно 7.
76. Фокусы гиперболы совпадают с фокусами эллипса
x2 y2
1.
25 9
Составить уравнение гиперболы, если её эксцентриситет равен 2.
77. Составить уравнение параболы, которая имеет фокус F(4, 3) и
директриса имеет уравнение y+1=0.
78. Составить уравнение параболы, которая имеет фокус F(2,–1) и
директриса имеет уравнение х – y –1=0.
79. Эллипс касается оси абсцисс в точке А(3, 0) и оси ординат в точке
В(0, –4). Составить уравнение этого эллипса, зная, что его оси симметрии
параллельны координатным осям.
80. Даны
вершина
параболы А(–2,–1) и уравнение её
директрисы
х+2y –1=0. Составить уравнение этой параболы, и найти
координаты фокуса параболы.
81. Привести к каноническому виду данное уравнение и построить
соответствующую линию:
а) 9x2–24xy+16y2-20x+110y–50=0;
б) 9x2+12xy+4y2–24x–16y+3=0;
в) 9x2+24xy+16y2–40x+30y=0;
г) 3x2+10xy+3y2–2x–14y–13=0;
д) 25x2–14xy+25y2+64x–64y–224=0;
е) 11x2–20xy–4y2–20x–8y+1=0;
ж) 4x2+4xy+y2+8x+6y+3=0.
з) 16x2–24xy+9y2–88x+66y+121=0;
к) x2+6xy+9y2–12x+24y+15=0;
л) x2+xy+y2+x+y=0.
18
СПРАВОЧНЫЙ МАТЕРИАЛ
ОПЕРАЦИИ НАД ВЕКТОРАМИ
СЛОЖЕНИЕ ВЕКТОРОВ
ПРАВЛО ТРЕУГОЛЬНИКА
b
а
В КООРДИНАТАХ
а b c
аа1 ,a2
b b1 , b2
а b
cа1 b1 ; a2 b2
РАЗНОСТЬ ВЕКТОРОВ
В КООРДИНАТАХ
а b
а
а
b d
d а1 b1 ; a2 b2
b
ПРАВИЛО ПАРАЛЛЕЛОГРАММА
b
а b
а
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
В КООРДИНАТАХ
b b1 , b2
а b
1. a b
2. а b , если 0
3. а b , если 0
а b
a b1 , b2
19
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
В КООРДИНАТАХ
аа1 ,a2 , b b1 , b2
а b = а · b сos ( а , b )
а b a1b1 a2b2
a а 2 а12 а22
длина вектора
a1b1 a2 b2
a b
cos
a b
a12 a22 b12 b22
угол между
векторами
a b a1b1 a2b2 0 условие перпендикулярности векторов
ПРЯМОУГОЛЬНЫЕ ДЕКАРТОВЫ КООРДИНАТЫ
М
y
B
A( x1 , y1 )
B( x2 , y 2 )
A
j
О i
AB{x2 x1 , y2 y1}
x
координаты вектора
AB ( x2 x1 )2 ( y2 y1 )2
длина вектора (расстояние между точками)
20
ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ
x1 x2
1
y y 2
y 1
1
B( x2 , y 2 )
x1 x2
2
y y2
y 1
2
x
A( x1 , y1 )
x
1
М ( x, y )
АМ
МВ
ПРЯМАЯ НА ПЛОСКОСТИ
Ax By C 0
общее уравнение прямой
(r r0 , n ) 0
n
у
M 0 ( x0 , y 0 ) a
n{ A, B} a
r0
r
A( x x0 ) B( y y0 ) 0
М0
х
О
M 0 ( x0 , y 0 ) a
a{a1 , a2 }
a
r r0 ta
a
у
x x0 y y0
a1
a2
М0
О
r
х
x x0 ta1
– параметрическое уравнение
y y0 ta2
21
каноническое
уравнение
M 1 ( x1 , y1 ) a
x x1
y y1
x2 x1 y 2 y1
у
M 2 ( x2 , y 2 ) a
уравнение прямой,
проходящей через 2 точки
М1
(а, 0) a
(0, b) a
М2
b
О
а
х
x y
1
a b
уравнение прямой
в отрезках
M 0 ( x0 , y 0 ) a
у
y y0 k ( x x0 )
y kx b
k tg
(0, b) a
b
М0
О
уравнение с
угловым
коэффициентом
х
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
у
а : Ax By C 0
M0
M 0 ( x0 , y0 ) а
х
О
а
( M 0 , a)
Ax0 By 0 C
22
A2 B 2
КРИВЫЕ ВТОРОГО ПОРЯДКА
ОКРУЖНОСТЬ
у
R
C (a, b); (C , R)
С
( x a ) 2 ( y b) 2 R 2
О
х
ЭЛЛИПС
а
е
а
е
у
В2
Р
А1 (а,0); А2 (0, а)
М
В1 (0,b); B2 (0, b)
r2
r1
F1 (c,0); F2 (0, c)
A1
F1
О
A2
F2
х
каноническое уравнение
В1
x2 y2
1
a2 b2
r1 a ex
x
a
e
b a2 c2
r2 a ex
e
Р ( х0 , у 0 )
xх0 yу0
2 1
a2
b
уравнение касательной
23
c
; (e 1)
a
ГИПЕРБОЛА
а
е
а
е
у
В2
r1
М
А1 (а,0); А2 (0, а)
r2
В1 (0,b); B2 (0, b)
F1 (c,0); F2 (0, c)
F1
О
A1
A2
х
F2
каноническое уравнение
В1
x2 y2
2 1
2
a
b
r1 a ex ; r2 a ex
для точки правой «ветви»
x
a
e
b с2 а2
r1 a ex ; r2 a ex
для точки левой «ветви»
e
c
; (e 1)
a
Р ( х0 , у 0 )
xх0 yу0
2 1
a2
b
уравнение касательной
ПАРАБОЛА
р
2
у
p
F ( ,0 )
2
y 2 2 px
r x
p
2
М
d: x
p
2
r
Р ( х0 , у 0 )
О
yy0 p( x x0 )
уравнение касательной
F
Р
24
х
СХЕМА ПРИВЕДЕНИЯ УРАВНЕНИЯ ЛИНИИ ВТОРОГО
ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ
Пусть задано уравнение линии второго порядка:
а11 х 2 2а12 ху а22 у 2 2а10 х 2а20 у а00 0
1. Определить коэффициенты а11, а22, а12, а10, а20, а00.
2. Найти корни характеристического уравнения:
а11
а12
а21
а22
0.
3. Найти координаты векторов i cos ; sin , j - sin ; cos
по формулам:
sin
tg
1 tg 2
, cos
1
1 tg 2
4. Вычислить коэффициенты уравнения кривой в новой системе
координат
1 , a22
2 , a12
a11
0
a10 cos a20 sin , a20
a10 sin a20 cos
a10
5. Переносом начала координат получить каноническое уравнение
линии.
6. Построить систему координат ( O ,i ' , j ' ) по координатам точки O
и векторов i ' , j ' .
7. Построить линию в этой системе координат.
25
ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ КООРДИНАТ
АФФИННАЯ СИСТЕМА КООРДИНАТ
х с11 х с12 у х0
у с21 х с22 у у0
Замена координатных
векторов
Перенос начала
х х х0
у у у0
х с11х с12 у
у с21х с22 у
ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
х хсos у sin х0
у х sin у cos у0
1, если ( O ,i , j ) и ( O ,i ' , j ' )
ориентированы одинаково
1, если ( O ,i , j ) и ( O ,i ' , j ' )
ориентированы противоположно
26
ДВИЖЕНИЯ ПЛОСКОСТИ
ДВИЖЕНИЯ 1-го РОДА
перенос на вектор а ( Т а )
1. Параллельный
а
Т
М1
М
а
: М М1
2. Поворот вокруг точки О на угол ( Ro )
Ro : М М1
М1
О
М
3. Центральная симметрия ( Z O ) ,
180о
Z O ( М ) М 1 , так, что
О
М1
МО ОМ1
М
ДВИЖЕНИЯ 2-го РОДА
1. Осевая симметрия ( S l )
l
S :М М
l
1
(MМ1 ) l и ММ 0 М 0 М1
М
Мо
М1
2. Скользящая симметрия f Ta Sl
М
a
Sl (М ) М1 , где
l
К
М1
~
М
27
(MМ1 ) l и МК КМ1
~
~
Ta ( М 1 ) М : М1М а
~
Ta Sl : М М
