Детерминированным КА
advertisement
Тема 4: Детерминированные и недетерминированные конечные
автоматы
Определение: Конечный автомат является детерминированным, если
для любого состояния q и любого символа a Σ, δ(q , a) содержит не более
одного элемента (δ(q, a)={q' } или δ(q, a)={ }.
Пример
КА
из
предыдущей
темы
является
полным
и
детерминированным:
КА=(Σ, Q, q0, δ, F), Σ={a,b}, Q={q0, q1, q2}, F={q2} δ: δ(q0,
b)={q0}, δ(q0, a)={q1}, δ(q1, a)={q1}, δ(q1, b)={q2}, δ(q2, a)={q1},
δ(q2, b)={q0}.
q0
a
q1
a
b
a
b
b
q2
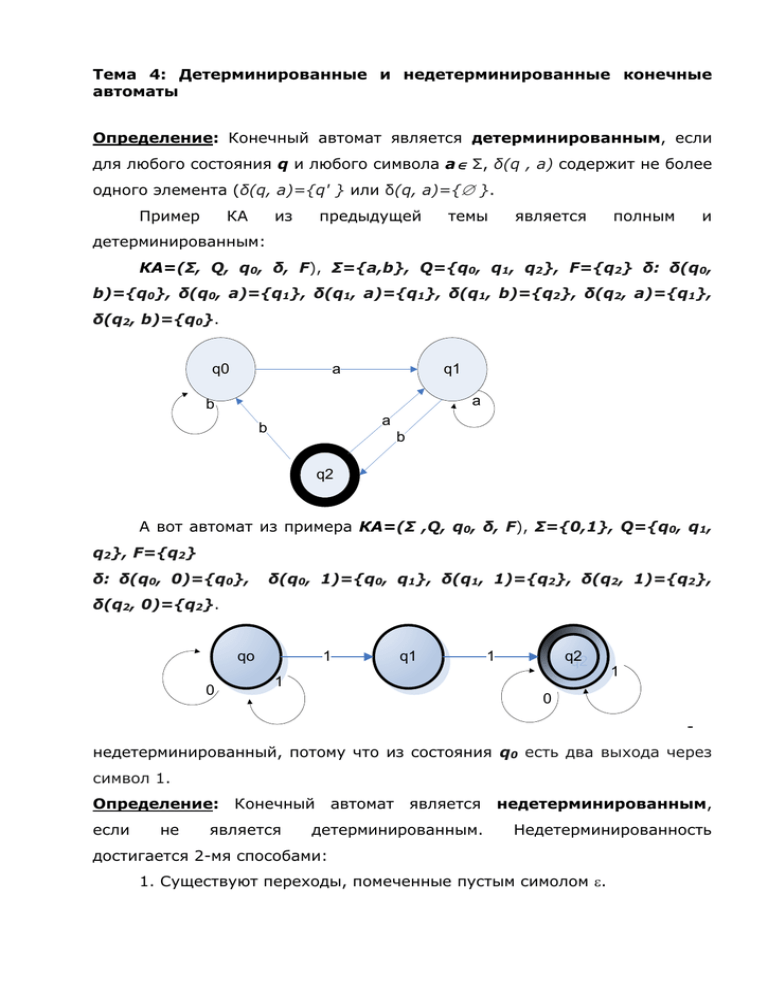
А вот автомат из примера КА=(Σ ,Q, q0, δ, F), Σ={0,1}, Q={q0, q1,
q2}, F={q2}
δ: δ(q0, 0)={q0},
δ(q0, 1)={q0, q1}, δ(q1, 1)={q2}, δ(q2, 1)={q2},
δ(q2, 0)={q2}.
qo
0
1
q1
1
q2
q2
1
1
0
недетерминированный, потому что из состояния q0 есть два выхода через
символ 1.
Определение: Конечный автомат является
если
не
является
детерминированным.
недетерминированным,
Недетерминированность
достигается 2-мя способами:
1. Существуют переходы, помеченные пустым симолом .
q1
a
q2
eps
b
eps
q0
q5
q5
eps
eps
q3
a
b
q4
2. Из одного состояния выходят несколько переходов, помеченных
одним и тем же символом.
Два конечных автомата эквивалентны, если они распознают один и
тот же язык.
То есть КА1 и КА2 эквивалентны если L( КА1)=L(КА2).
Теорема: Для любого недетерминированного конечного автомата можно
построить эквивалентный детерминированный конечный автомат.
Алгоритм преобразования недетерминированного КА в детерминированный
КА.
Пусть будет недетерминированный конечный автомат НДКА=(Q, Σ,
q0, δ, F) необходимо построить ДКА= (Q', Σ, [q0 ], δ', F').
Состояния из Q' будут комбинациями состояний из начального
автомата [q0,q1,...,qn], qiQ. Возможны подмножества этих состояний.
Шаг 1. Вначале Q'={[q0]}, где [q0] это пока немаркированное
состояние. Маркированым становится то состояние для которого
проанализированы все переходы из данного состояния.
Шаг 2. Для всех элементов
[q0,q1,...,qm]Q' и aΣ проанализируем
переходы δ({q0,q1,...,qm},a). Обозначим новые полученные состояния
как [qi0,qi1,...,qim].
Шаг 2.1. Вводим полученные состояние [qi0,qi1,..,qim] в множество
Q' немаркированных.
Шаг 2.2. Для этих состояний рассматриваем
δ'({q0,q1,...,qm},a) =
δ'({q0,q1,...,qm},a) [qi0,qi1,...,qim].
Шаг 2.3. Маркируем состояния [qi0,qi1,...,qim] из Q'.
Шаг 3. Повторяется Шаг 2 для всех немаркированных состояний из Q'.
Шаг 4. В качестве финальных состояний нового детерминированного
КА F'={[qi0,qi1,...,qim]}, вводятся те состояния для которых хотя бы
одно из состояний qi0,qi1,...,qim является конечным/финальным в
начальном недетерминированном КА.
Шаг 5. Стоп.





