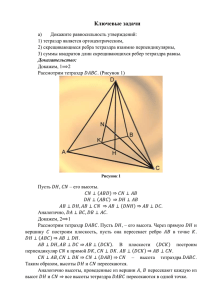
Методика решения стереометрических задач

Муковнина
Людмила Михайловна
Учитель математики
ГОУ СОШ № 250
Материалы к уроку по подготовке к ЕГЭ
(решение стереометрических задач).
Цель: повторить теоретический материал, показать практическое его применение в
решении стереометрических задач.
Задача 1: Ребро правильного тетраэдра равно 1. Первый шар вписан в этот тетраэдр.
Второй шар касается вписанного шара и трёх граней тетраэдра. Найдите радиус второго
шара.
Решение: (первый способ)
P
1.
Точка О – центр сферы, вписанной в
тетраэдр:
А0
O1
а) O  PH ,(О – высота тетраэдра)
C0
B0
O
б) точка О лежит на биссектрисе
F
С
А
т. О – равноудалена от (АВС) и
(РВС)
К
H
угла HKP
ОН = r – радиус сферы.
В
a3  R 3; a3  1; R 
1. ∆АВС
∆PHK: PH 
3. ∆PHK:
по
равносторонний:
1
 HC ,
3
HK 
2.
–
1
2 3
; AK  PK 
3
2
2
3
свойству
биссектрисы
угла
треугольника:
r 1
OH HK
r
1 2
1 OH 1
 ; ò î ãäà :  ,

;

 ,
h 4
OP PK
2
2 3  3 3 OP 3
r
3
1
Следовательно 3r 
2
2
2
6
 r ; 4r 
;r 

3
3
4 3 12
PH
2 6

:
 2 , таким образом А0, В0, С0 – середины рёбер тетраэдра,
2r
3 6
4.
r1 – радиус сферы, вписанной в тетраэдр РА0В0С0.
Ответ:
r1 
6
24
6
24
Решение: (второй способ)
Задача решается значительно проще, если знать, что радиус r вписанной сферы в
правильный тетраэдр выражается формулой: r 
h  PH 
1
h
4
a 6
2
2
, r
или r 
, где а – ребро тетраэдра.
12
3
4 3
1
1 1 2
2
Далее: либо h1  h; r1   
, (h1 – высота тетраэдра РА0В0С0, r1 – радиус)

2
4 2 3 8 3
либо a1 
Ответ:
1
1 6
6
a; r1 

.
2
2 12 24
6
24
Задача 2: Через середины рёбер АВ и АС прямой треугольной призмы ABCA1 B1C1 и
точку В1 Проведено сечение призмы, которое разделило призму на два многогранника.
Найдите больший из объёмов этих многогранников, если объём призмы равен 12.
P
Решение:
1. AA1  h; S A1C1B1  S ; S  h  12
2. Продлим NC1, MB1 и АА1 – пересечение точка
А
В
M
N
Р.
3. S ANM 
С
1
S
4
( A1C1B1AMN )
РА = АА1 = h.
А1
1 1
1
1
В1 4. V
h  S  hS  12  1
PAMN 
3
С1
4
12
12
1
2
2
VPA1C1B1  2h  S  hS  12  8
3
3
3
2
VA1C1B1 AMN  8  1  7
Ответ: 7.
Задача 3: Точки Р и Т – середины рёбер МС и MD четырёхугольной пирамиды
MABCD, в основании которой лежит параллелограмм ABCD. Объём пирамиды MABCD
равен 80. Найдите объём пирамиды MABPT.
M
Решение:
T
Метод решения – разбиение данной фигуры на
многогранники, объёмы которых можно найти.
P
1. VMABD  VMBCD , так как S ABD  S BCD и h – высота
B
C пирамиды – общая.
Таким образом VABMD  40 .
2. S BMT  S BTD , так как MT = TD.
А
D
4.
1
3. VABMT  VABTD   40  20
2
Пирамиду MABPT разбиваем на две: MABT и MBPT – с общей высотой, но
S BPT 
1
1
1
S ABT , так как TP  DC  AB , ТР║АВ, ∆АВТ и ∆ВРТ – с общей высотой.
2
2
2
1
1
VMBPT  VMABT   20  10
2
2
5. VMABPT  VMABT  VMBPT  20  10  30
Ответ: 30.
Задача 4: В Конусе с вершиной М проведены три образующие МА, МВ и МС,
причём АВ – диаметр основания конуса, а отношение длины меньшей дуги АС к меньшей
дуге СВ равно 2. Высота конуса равна радиусу его основания. Найдите синус угла между
медианой CL треугольника ВСМ и плоскостью АСМ.
M
Решение:
1. OM = OB = OA = r,
L1
 AC  120; CB  60 , т. о. СО = ОВ
L
= СВ = r.
С
В
О
А
2. AB  r ; CB  2r ; AC  r 3
К
3
3. MO   ACB  ; LK  OB; LM  LB , значит К – середина ОВ и LK 
4. ∆СОВ – равносторонний, СК – высота (К – середина ОВ), CK 
1
r.
2
r 3
.
2
2
2
r r 3
5. LK║MO, тогда ∆CKL – прямоугольный ( K  90 ), CL     
 r.
 2   2 
1
1 1
r3 3
6. VMACB  S ACB  MO    r 3  r  r 
3
3 2
6
1
1
7. VMACB  VBMAC ;VLMAC  VBMAC  S AMC  LL1
2
3
8.
r
r
r 2
r
9.
A
r 2
r
1
AM  MC  MB  r 2
M
D
r 3
r
r 2
r
C
1
r 5 r 2 15
r2 3 r 5

MD  2r 

, S AMC  r 3 
2
2
4
4
2
1 r 2 15
r3 3
 LL1 
10. VLMAC  
,
3
4
6
Ответ:
 LL   AMC 
2
LL1 
r
5
11. sin  CL  ACM   
LL1
r
1


CL
5 r
5
1
5
4