xxxxxxxxxxxxxx
advertisement
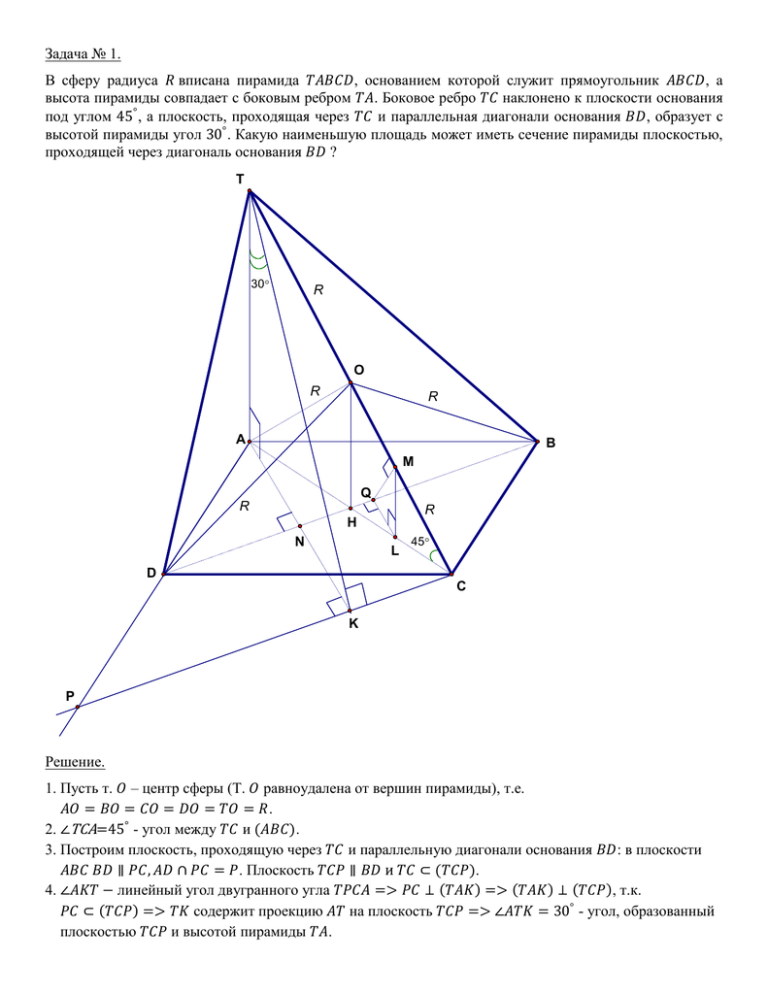
Задача № 1. В сферу радиуса 𝑅 вписана пирамида 𝑇𝐴𝐵𝐶𝐷, основанием которой служит прямоугольник 𝐴𝐵𝐶𝐷, а высота пирамиды совпадает с боковым ребром 𝑇𝐴. Боковое ребро 𝑇𝐶 наклонено к плоскости основания под углом 45° , а плоскость, проходящая через 𝑇𝐶 и параллельная диагонали основания 𝐵𝐷, образует с высотой пирамиды угол 30° . Какую наименьшую площадь может иметь сечение пирамиды плоскостью, проходящей через диагональ основания 𝐵𝐷 ? T 30 R O R R A B M Q R R H N L 45 D C K P Решение. 1. Пусть т. 𝑂 – центр сферы (Т. 𝑂 равноудалена от вершин пирамиды), т.е. 𝐴𝑂 = 𝐵𝑂 = 𝐶𝑂 = 𝐷𝑂 = 𝑇𝑂 = 𝑅. 2. ∠TCA=45° - угол между 𝑇𝐶 и (𝐴𝐵𝐶). 3. Построим плоскость, проходящую через 𝑇𝐶 и параллельную диагонали основания 𝐵𝐷: в плоскости 𝐴𝐵𝐶 𝐵𝐷 ∥ 𝑃𝐶, 𝐴𝐷 ∩ 𝑃𝐶 = 𝑃. Плоскость 𝑇𝐶𝑃 ∥ 𝐵𝐷 и 𝑇𝐶 ⊂ (𝑇𝐶𝑃). 4. ∠𝐴𝐾𝑇 − линейный угол двугранного угла 𝑇𝑃𝐶𝐴 => 𝑃𝐶 ⊥ (𝑇𝐴𝐾) => (𝑇𝐴𝐾) ⊥ (𝑇𝐶𝑃), т.к. 𝑃𝐶 ⊂ (𝑇𝐶𝑃) => 𝑇𝐾 содержит проекцию 𝐴𝑇 на плоскость 𝑇𝐶𝑃 => ∠𝐴𝑇𝐾 = 30° - угол, образованный плоскостью 𝑇𝐶𝑃 и высотой пирамиды 𝑇𝐴. 5. Сечение пирамиды плоскостью, проходящей через диагональ основания 𝐵𝐷, − ∆𝐵𝐷𝑀, вершина которого 𝑀 лежит на ребре 𝑇𝐶. Площадь этого треугольника тем меньше, чем меньше его высота. 1 6. ∆𝑇𝐴𝐶: 𝑇𝐶 = 2𝑅; ∠𝑇𝐴𝐶 = 90° ; ∠TCA=45° => 𝑇𝐴 = 𝐴𝐶 = 𝑅√2; 𝐴𝐻 = 𝐻𝐶 = 2 𝐴𝐶 = 𝑅√2 2 . 7. ∆𝐴𝑁𝐻 подобен ∆𝐿𝑄𝐻 по двум углам, т.к. ∠ANH=∠LQH=90° ; ∠AHN=∠LHQ как вертикальные => 𝐴𝑁 𝑄𝐿 = 𝐴𝐻 1 1 1 ; 𝐴𝑁 = 2 𝐴𝐾 = 2 𝑇𝐴 ∙ 𝑡𝑔30° = 2 𝑅√2 ∙ 𝐻𝐿 1 1 √3 𝐻𝐿2 8. ∆𝑄𝑀𝐿: 𝑄𝑀 = √𝑄𝐿2 + 𝑀𝐿2 = √𝑄𝐿2 + 𝐿𝐶 2 = √ 2 = 2 𝑅√3 = 3 𝑅 √6 𝑅 √6 . Т.о. 𝑄𝐿 𝐻𝐿2 + 3 𝑅2 2 4 4 ℎ′ (𝑥) = 8 𝑥−𝑅√2 3 , ℎ′ (𝑥) = 0, если 2 4 𝑅 2√ 𝑥 2 −𝑅√2∙𝑥+ 3 ℎ′ (𝑥) | 0 3√2∙𝑅 , 0<𝑥< 𝑅2 2 2 = 𝐻𝐿 √3 | | 3√2∙𝑅 𝑅√2 8 2 3√2∙𝑅 8 − 𝐿𝐶; 𝐿𝐶 = 𝑅√2 2 − 𝐻𝐿). . 𝑅√2 2 𝑥 − 𝑅√2 = 0, т. е. 𝑥 = 3 3√2∙𝑅 8 4 , (2√3 𝑥 2 − 𝑅√2 ∙ 𝑥 + 𝑅2 2 > 0). 3 функция достигает своего наименьшего значения 6 𝑅2 4 ) = √8 𝑅 2 − 8 𝑅 2 + 8 𝑅 2 = √ 8 = 1 1 𝑅2 4 𝑅√2 4 = 𝑅2 4 𝑅√2 4 . 2 + 𝑆 = 2 ∙ 𝐵𝐷 ∙ ℎ = 2 𝑅√2 ∙ Ответ: 2 𝑅√2 𝑅∙𝐻𝐿∙2 √6∙𝑅√2 𝑥 В точке 𝑥 = 8 ; 𝑄𝐿 = 2 − ℎ(𝑥) ℎ( 𝑅2 8 𝐻𝐿 2 − 𝑅√2 ∙ 𝐻𝐿 + 𝐻𝐿2 = √3 𝐻𝐿2 − 𝑅√2 ∙ 𝐻𝐿 + Рассмотрим функцию ℎ(𝑥) = √3 𝑥 2 − 𝑅√2 ∙ 𝑥 + 𝑅√2 2 𝐻𝐿 𝑅√2 + 𝐿𝐶 2 = √ 3 + ( 2 − 𝐻𝐿) (в. ∆𝑀𝐿𝐶 ∠𝑀𝐿𝐶 = 90° ; ∠𝑀С𝐿 = 45° => 𝑀𝐿 = 𝐿𝐶; 𝐻𝐿 = 𝐻𝐶 − 𝐿𝐶 = Т. о. 𝑄𝑀 = ℎ = √ = . . (𝐵𝐷 = 𝐴𝐶 как диагонали прямоугольника). . Замечание: Возможен другой способ решения задачи, если замети, что высота 𝑀𝑄 треугольника 𝐵𝐷𝑀 будет наименьшей, если 𝑀𝑄 ⊥ 𝑇𝐶 (т. 𝑄 ∈ 𝐵𝐷, |𝑄𝑀| − расстояние от т. 𝑄 до 𝑇𝐶); 𝑄𝑀 – общий перпендикуляр между скрещивающимися прямыми 𝑇𝐶 и𝐵𝐷.





















