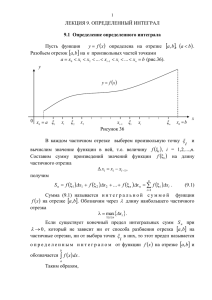
Определенный интеграл

Упражнения по теме «Определенный интеграл»
УПРАЖНЕНИЯ
по теме «Определенный интеграл»
1. Касательная к графику функции y = f (x) в точке M 1 (a; f (a )) со-
ставляет с осью Ox
π
угол
, а в точке
M 2 (b; f (b)) – угол
3
Функция f ′′( x) – непрерывна на [a; b] . Найти интегралы
b
π
4
.
b
∫ f ′′( x)dx
∫ f ′( x) ⋅ f ′′( x)dx .
и
a
a
e
∫
2. Докажите, что если J n = ln nxdx , то J n = e − n ⋅ J n −1 ( n ∈ ℕ).
1
3. Получить
рекуррентные
π 2
π 2
In =
∫ sin
n
xdx и K n =
формулы
∫ cos
n
для
вычисления
интегралов
xdx ( n ∈ ℕ и n ≥ 2 ).
0
0
4. Составить рекуррентную формулу и вычислить интеграл
0
In =
∫
x n e x dx ( n ∈ ℕ).
−1
5. Составить
рекуррентную
π 4
In =
∫ tg
n
формулу
для
вычисления
интеграла
xdx ( n ∈ ℕ и n ≥ 2 ).
0
1
6. Доказать справедливость равенства
∫x
1
m
∫
n
(1 − x) dx = x n (1 − x) m dx .
0
0
7. Показать, что если f (x) – функция периодическая с периодом T , то
a +T
∫ f (t )dt
не зависит от
a
(Подсказка: докажите, что он равен
a
T
∫ f (t )dt
при любом a ).
0
1
8*. Найдите
dx
∫ ( e x + 1)( x 2 + 1) .
−1
1
dt
=
9. Доказать справедливость равенства
2
1
+
t
x
∫
1
1x
dt
∫1+ t2
1
( x > 0) .
Упражнения по теме «Определенный интеграл»
tgx
tdt
10. Доказать справедливость равенства
+
2
1+ t
1e
∫
11. Докажите, что если функция
ctgx
∫
1e
dt
= 1.
2
t (1 + t )
f (x) – нечетная и периодическая с пе-
x
∫ f (t )dt
риодом T , то
также является периодической функцией с тем
a
же периодом. (Подсказка: используйте тот факт, что для периодичеa +T
ской функции с периодом T
∫ f (t )dt
не зависит от a ).
a
x
12. Показать, что если f (x) функция нечетная, то
∫ f (t )dt – функция четa
x
∫ f (t )dt – нечетной, если
ная. Будет ли
f (x) – четная?
a
13. Найдите производные:
b
⎞
⎞
⎞
⎛x
⎛b
d ⎛⎜
d
d
2
2
2
⎟
⎟
⎜
⎜
sin(t )dt ;
б)
sin(t )dt ;
в)
sin(t )dt ⎟ ;
а)
⎟
⎟
⎟
⎜
⎜
⎜
dx
dx
dx
⎠
⎠
⎠
⎝a
⎝a
⎝x
2
3
0
⎛x
⎞
⎛x
⎞
⎞
d ⎜
d ⎛⎜
d ⎜
3 ⎟
3 ⎟
3 ⎟
г)
1 + t dt ⎟ ;
д)
1 + t dt ;
е)
1 + t dt ⎟ .
⎟
dx ⎜ 2
dx ⎜⎜ 2
dx ⎜⎜
⎟
⎟
⎝x
⎠
⎝x
⎠
⎝0
⎠
14. Найти производную по x от функции y заданной
∫
∫
∫
∫
∫
∫
y
а) неявно:
∫e
t2
x
∫
dt + cos t 2 dt = 0 .
0
0
t2
2
u2
du .
y=
ln
u
2
u
du ,
б) параметрически: x =
ln u
∫
∫
2
t
15. Найти пределы:
x
∫ cos t dt
sin x
2
а) lim
0
x
x→0
;
∫
tg t dt
∫
sin t dt
0
tg
x → +0 x
б) lim
.
0
16. Найти точки экстремума и точки перегиба графика функции
x
∫
Φ ( x) = (t − 1)(t − 2) 2 dt . Построить график этой функции при a = 0 .
a
2
Упражнения по теме «Определенный интеграл»
17. Найдите
наибольшее
и
наименьшее
значение
функции
x
Φ( x) =
2t + 1
dt на отрезке [−1; 1] .
2
t
t
−
2
+
2
0
∫
x
18. Найдите длину линии, заданной уравнением y =
∫
cos t dt .
−π 2
Ответ: 4.
t
cos zdz
19. Найдите длину дуги линии x =
,
z
∫
1
t
y=
∫
1
sin zdz
от начала коz
ординат до ближайшей точки с вертикальной касательной.
Ответ: ln (π 2 ) .
+∞
20*. Найдите
dx
∫ ( x a + 1)( x 2 + 1)
( a – const).
0
3