А.А. Любушин
advertisement

ИССЛЕДОВАНИЕ СЛУЧАЙНЫХ ФЛУКТУАЦИЙ ГЕОФИЗИЧЕСКИХ ПОЛЕЙ
А.А. Любушин
Институт физики Земли РАН им. О.Ю.Шмидта, e-mail: lyubushin@yandex.ru
http://AlexeyLyubushin.narod.ru/Index.htm
В лекциях будет сделан обзор современных методов анализа временных рядов систем
геофизического мониторинга (в том числе и многомерных), будет описан пакет программ,
позволяющий провести этот анализ самостоятельно и предоставлены загрузочные модули таких
программ. Рассмотрены примеры анализа данных геофизического мониторинга.
Временные ряды - это одна из наиболее распространенных форм представления исходных
данных систем мониторинга в задачах геофизики, метеорологии, экологии. Последовательные
значения исследуемых характеристик отражают как внутреннюю динамику объектов, так и их
взаимные связи и изменчивость этих связей во времени. Сами временные ряды могут отличаться как
физической природой измеряемых величин, так и пространственным положением пунктов
измерения.
Одна из наиболее традиционных моделей временных рядов заключается в разделении
наблюдений на низкочастотный сигнал (тренд) и высокочастотный шум. Анализ гладких, или
трендовых, составляющих сигналов мониторинга важен, но он, как правило, не приносит новой
информации. Ниже предлагается обратить внимание на высокочастотную составляющую,
пренебрежимо называемую "шумом". Как оказалось, именно структура шума дает принципиально
новую и скрытую информацию. Иными словами, часто именно шум оказывается сигналом.
План дальнейшего изложения:
1. Спектры мощности и спектрально-временные диаграммы.
2. Гауссовские и локально-полиномиальные тренды.
3. Непрерывные вейвлет-диаграммы.
4. Ортогональные вейвлет-разложения.
5. Мульти-фрактальный анализ временных рядов.
6. Канонические когерентности и спектральные меры синхронного поведения.
Реализация пунктов 1-5 выполнена в интерактивном программном пакете Spectra_Analyzer
[Любушин, 2006], который может быть свободно скачан по адресам:
http://alexeylyubushin.narod.ru/SpAn.zip
http://old.ifz.ru/scient_directions/data_monitoring/01/SpAn.zip
Руководство пользователя программным пакетом на русском языке доступно по адресам:
http://alexeylyubushin.narod.ru/Software_for_Monitoring_Systems/Spectra_Analyzer/Spectra_Analyz
er_RUS.pdf
http://old.ifz.ru/scient_directions/data_monitoring/01/Spectra_Analyzer.pdf
В монографии [Любушин, 2007] содержание лекций представлено в более подробном
изложении.
Входным файлом для используемых ниже программ может служить любая символьная таблица
чисел, в первой колонке которой стоят числа, интерпретируемые как значения временного ряда.
Прочие колонки входного файла, если таковые имеются, игнорируются.
СПЕКТРЫ МОЩНОСТИ И СПЕКТРАЛЬНО-ВРЕМЕННЫЕ ДИАГРАММЫ
Для оценки спектра мощности скалярного временного ряда в дальнейшем будет использоваться
параметрическая авторегрессионная оценка [Kanasewich, 1981; Marple, 1987]. Пусть x(t ) –
стационарный в широком смысле временной ряд, t 1,..., N - дискретный временной индекс,
нумерующий последовательные отсчеты. Далее в выкладках для простоты будем считать, что шаг по
времени t 1 . Модель авторегрессии порядка p 0 (AR(p)-модель) представляет собой уравнение:
p
x(t ) ak x(t k ) (t ) d ,
(1)
k 1
где ak – коэффициенты авторегрессии (параметры модели), d – параметр статического смещения,
(t ) – белый шум с нулевым средним и дисперсией 2 . Введем ( p 1) -мерные векторы:
Y (t ) ( x(t 1),..., x(t p),1)T , c (a1,..., a p , d )T
(2)
и запишем (1) в компактной форме: x(t ) c Y (t ) (t ) .
Пусть имеется конечная выборка { x(t ), t 1,..., N } . Тогда оценка вектора параметров c из
T
N
условия минимума суммы квадратов остатков
2
(t ) min сводится к решению системы
t p 1
нормальных уравнений с симметричной положительно определенной матрицей A :
Ac R,
A
N
Y (t )Y
t p 1
N
T
(t ), R x(t )Y (t )
(3)
t p 1
Решение уравнений (3) автоматически удовлетворяет условию устойчивости AR(p)-модели: все
корни полинома p
p
a
k 1
k
p k
по модулю строго меньше 1 [Marple, 1987; Box, Jenkins, 1970].
Однако при больших порядках p решение системы (3) становится достаточно трудоемким, особенно
если его надо решать многократно. Поэтому обычно предполагают стационарность выборки, от
параметра d освобождаются тем, что вычитают из значений выборочную оценку среднего, а
элементы aij матрицы A размером теперь уже p p заменяют на значения |i j| , где k –
выборочные оценки ковариационной последовательности M {x(t ) x(t k )} , M {...} – знак
математического ожидания. В этом случае матрица A становится теплицевой (симметричной
неотрицательно определенной и по всем диагоналям стоят одинаковые элементы), для обращения
которой существует быстрый итерационный метод Дарбина-Левинсона [Kanasewich, 1981; Marple,
1987], при котором порядок авторегрессии последовательно увеличивается от 1-го до искомого на
единицу. Полученная таким образом оценка параметров AR(p)-модели известна как оценка ЮлаУолкера. Однако эта оценка довольно часто теряет устойчивость при выполнении итераций ДарбинаЛевинсона, особенно если теплицева матрица A имеет диагонали, на которых стоят значения,
близкие к значениям на главной диагонали матрицы (при наличии сильных монохроматических
компонент в сигнале).
В 1969 году Бургом была предложена модификация метода Юла-Уолкера, состоящая попрежнему в использовании итераций Дарбина-Левинсона в последовательном увеличении порядка
авторегрессии. Однако на этот раз при каждом увеличении порядка p 1 p эти итерации
используются лишь для изменения «старых» коэффициентов a j , j 1,...,( p 1) , а каждый «новый»
коэффициент a p (старший коэффициент модели AR(p), известный также как «коэффициент
отражения»), находится из условия минимума суммы квадратов ошибок прогноза на шаг вперед и
назад в силу AR(p)-модели. Одновременно для каждого текущего порядка модели авторегрессии,
увеличивающегося от 1 до p , находится оценка дисперсии 2 . Этот метод, который подробно
изложен в [Marple, 1987], оказался исключительно эффективным и устойчивым.
После определения значений параметров модели (1) они могут быть использованы для
построения параметрической оценки спектра мощности временного ряда:
p
S xx ( ) 2 2 |1 ak eik |2 ,
k 1
(4)
которая следует из представления Крамера [Brillinger, 1975] для стационарной случайной
последовательности, – частота. Формула (4) применяется для дискретного набора частот
k 2 (k 1) / N , k 1,..., N . Для такого набора значений частот значения Фурье-компонент
d x( N ) (k ) в дискретном Фурье-разложении выборки d x( N ) (k ) t 1 x(t ) exp(ik t ) при N
N
являются асимптотически независимыми [Brillinger, 1975]. Для вещественного временного ряда
спектр мощности симметричен относительно частоты Найквиста , поэтому его рассматривают
для значений частот 0 k . Размерность спектра мощности совпадает с размерностью
дисперсии временного ряда, но следует помнить, что спектр мощности – это лишь малая часть
дисперсии сигнала для колебаний с частотами от k до k 1 .
Первичным параметром модели (1) является порядок авторегрессии p . Несмотря на
многочисленные попытки дать формальный критерий определения оптимального порядка p , эта
задача так и нашла окончательного решения, а предлагаемые методы не выходят за рамки
эмпирических правил. Порядок AR-модели меняется для одних и тех же данных в зависимости от
целей использования [Kashyap, Rao, 1976]. Для прогноза на один или несколько шагов вперед
порядок обычно небольшой и редко достигает 10. Если же целью является получение
параметрической спектральной оценки (4), то порядок p имеет смысл брать значительным:
p N /10 N / 4 . При этом надо иметь в виду, что чем больше порядок, тем чувствительнее оценка,
но, одновременно, тем она более неустойчива и содержит больше статистических флуктуаций.
Пусть число отсчетов N временного ряда достаточно велико и его спектральные свойства
медленно меняются со временем. Тогда можно рассмотреть задачу оценки эволюции спектра
мощности в скользящем временном окне некоторой длины L N со взаимным смещением L
значений. Пусть – временная координата правого конца текущего временного окна. Оценим для
отсчетов L 1 t модель AR(p) и вычислим оценку спектра мощности (4). В этом случае ее
можно записать в виде, подчеркивающем зависимость от положения и длины окна:
S xx S xx (, | L) . С учетом разрешения по частоте 2 / L на выборке длиной L отсчетов,
формулу (4) имеет смысл применять для значений частот j 2 j / L,
j 1,...,( L 1) / 2 .
Усл.ед.
-30
Град. C
(б)
1.2
(а)
12.8
205
1
-32
0.8
5.4
-34
19.5
0.6
54
0.4
-36
0.2
Годы
-38
0
600
800
1000
1200
1400
1600
1800
10
100
1000
Период, годы
Рис. 1. Спектральный анализ временного ряда реконструкции зимних температур в Гренландии
Построение двумерных карт или рельефов S xx (, | L) на плоскости «частота-время» ( , ) в
русскоязычной литературе традиционно имеет аббревиатуру СВАН (спектрально-временной анализ).
Обычно для этой цели используется дискретное преобразование Фурье от выборки в текущем
временном окне, вычисление периодограммы и ее усреднение по частотам тем или иным способом
для уменьшения дисперсии оценки. Опыт показывает, что использование AR-модели дает более
устойчивые результаты. Кроме того, при использовании оценки (4) отсутствуют побочные эффекты,
связанные с цикличностью дискретного преобразования Фурье от конечной выборки [3, 6].
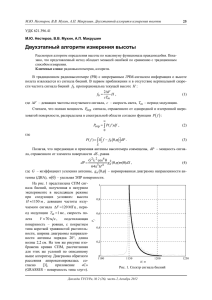
В качестве примера применения спектрального и спектрально-временного анализа рассмотрим
временной ряд реконструкций зимних температур в Гренландии [Dansgaard et al, 1975]. На рис. 1, а
серыми линиями представлен график ежегодных реконструированных зимних температур за период
553-1973 гг. Толстыми синими линиями изображен график средних значений температур в
последовательных фрагментах длиной 10 лет. На рис. 1, б приведен график оценки спектра мощности
ряда по всей выборке с использованием модели AR(150) при общей длине ряда 1421 отсчет. Пять
наиболее высоких спектральных пика помечены значениями периодов, на которых реализуется
локальные максимумы. Эти периоды отражают определенные климатические циклы, из которых для
задач краткосрочного прогноза глобальной температуры наибольший интерес представляют
низкочастотные с периодами 54 и 205 лет [Lyubushin, Klyashtorin, 1975].
На рис. 1, в представлена частотно-временная диаграмма эволюции десятичного логарифма
спектра мощности в скользящем окне длиной L = 500 лет с взаимным смещением L = 10 лет. В
каждом окне строилась AR(50)-оценка. Чтобы более подробно (с большим разрешением по частоте)
исследовать динамику низкочастотных спектральных пиков, рассмотрим ряд 10-летных средних
значений (синяя линия на рис. 1, а). Спектрально-временная диаграмма для этого временного ряда
представлена на рис. 1, г. Для нее оценка производилась в скользящем временном окне длиной 50
отсчетов (то есть те же 500 лет) с минимальным смещением в 1 отсчет и порядком авторегрессии 10.
Из рис. 1, г видно, что 200-летний пик существовал лишь до 1350 года. Далее этот пик стал
эволюционировать в сторону более высоких частот и в интервале 1250-1750 гг. он слился с 25-30летним гребнем диаграммы и сформировал спектральный пик примерно с периодами 50-60 лет.
ГАУССОВСКИЕ И ЛОКАЛЬНО-ПОЛИНОМИАЛЬНЫЕ ТРЕНДЫ
Оценка тренда может быть рассмотрена как процедура сглаживания данных. Одним из
популярных методов сглаживания является использование ядерных функций [Hardle, 1989]. Пусть
y ( s) - произвольный ограниченный интегрируемый сигнал с непрерывным временем. Назовем
ядерным усреднением с параметром масштаба H 0 среднее значение y ( s | H ) в момент времени
s , вычисляемое по формуле:
y (s | H )
y( s H ) ( ) d
( ) d ,
(5)
где ( ) - произвольная неотрицательная ограниченная симметричная интегрируемая функция,
называемая ядром усреднения. Если ( ) exp( ) , то назовем величину y ( s | H ) гауссовским
трендом с параметром (радиусом) усреднения H . Для сигналов с дискретным временем вычисление
ядерных трендов может быть эффективно реализовано с помощью быстрого преобразования Фурье.
Гауссовский тренд относится к классу непараметрических трендов, которые целесообразно
применять тогда, когда нет априорной информации о виде низкочастотных вариаций ряда.
Другим способом сглаживания временного ряда является использование локальных полиномов
[Hardle, 1989]. В этом способе вычисления тренда для каждого временного отсчета
рассматривается его окрестность радиуса, равного заданному числу m отсчетов, то есть
рассматриваются временные индексы t : m t t m . В этой окрестности к фрагменту
временного ряда методом наименьших квадратов подгоняется полином заданного порядка p и
качестве локального среднего в точке берется значение полинома в этой точке. Подобный способ
сглаживания допускает быструю реализацию методом Савицкого-Голея [Press et al, 1996a].
На рис. 2 приведены результаты сглаживания одного и того же временного ряда (вертикальных
сейсмических колебаний с шагом по времени 1 минута длительность 15 суток) гуассовским (рис. 2, а)
и локально-полиномиальным (рис. 2, б) трендом.
2
НЕПРЕРЫВНЫЕ ВЕЙВЛЕТ-ДИАГРАММЫ
Методическим недостатком СВАН является использование окна. Если окно слишком велико,
то частотно-временная диаграмма неспособна реагировать на быстрые изменения спектрального
состава и на наличие короткоживущих сигналов – всплесков. Для достижения этой цели необходимо
уменьшить длину L . Но слишком малая длина окна приводит к увеличению чисто статистических
флуктуаций текущих оценок спектров и СВАН-диаграмма становится слишком зашумленной и
малоинформативной. Необходимо находить компромисс между устойчивостью и чувствительностью
и эмпирически перебирать длины L , причем для каждого значения длины надо следить, чтобы
используемый порядок авторегрессии p был свой (уменьшался и увеличивался пропорционально
L ). При изменении длины L одновременно меняется и максимально допустимый к рассмотрению
период.
Непрерывные вейвлет-преобразования [Daubechies, 1992; Chui, 1992; Mallat, 1998] призваны
устранить эти недостатки и, кроме того, дать возможность отобразить на одной диаграмме сразу все
интересующие периоды. Пусть (t ) - некоторая быстроубывающая функция, удовлетворяющая
условию допустимости:
(t ) dt 0 и условию нормировки:
| (t ) |
2
dt 1 . Непрерывным
вейвлет-преобразованием сигнала x( s) называется величина, зависящая от двух параметров
(t , a), a 0 :
Wx(t , a)
1
a
s t
x(s) a ds a x(t av) (v) dv .
(6)
0
(а)
-10000
Рис. 2, а. Сглаживание сейсмической
записи с шагом по времени 1 минута
(серая линия) гауссовским трендом
(синяя линия) с параметром ядра
H 100 отсчетов
-20000
-30000
-40000
-50000
0
5000
10000
15000
20000
0
(б)
-10000
Рис. 2, б. Сглаживание сейсмической
записи с шагом по времени 1 минута
(серая линия)
локальнополиномиальным трендом (синяя линия)
второго порядка ( p 2 ) в скользящем
-20000
-30000
окне радиуса
-40000
-50000
0
5000
10000
15000
20000
m 100 отсчетов
Здесь t - момент времени, a 0 - параметр масштаба, который далее часто будем называть
более привычным термином «период». Величина (6) отражает поведение исследуемого сигнала в
окрестности точки t с характерным масштабом вариаций a . Для сигнала с дискретным временем
вычисление величин (6) может быть эффективно реализовано с помощью быстрого преобразования
Фурье. Нашей непосредственной целью является построение 2-мерной карты значений модуля
величины (6): | Wx(t , a) | , которая дает наглядное представление о динамике возникновения,
эволюции и исчезновения «характерных периодов» короткоживущих всплесков исследуемого
сигнала. Естественно, что величина (6) сильно зависит от выбора функции (t ) . Выбор той или иной
функции (t ) определяется тем, какого вида короткоживущие сигналы мы хотим изучать.
Следует подчеркнуть, что для конечной выборки и для данного масштаба a на концах
временного интервала существуют «мертвые» отрезки времени, такие, что для моментов времени t ,
принадлежащих этим отрезкам, «не хватает» данных либо слева, либо справа от точки t для
вычисления (6). При использовании быстрого преобразования Фурье сигнал рассматривается на
кольце и поэтому, если он содержит сильный низкочастотный тренд, то для моментов времени t ,
близких к началу и к концу выборки, возникают сильные всплески значений | Wx(t , a) | , которые
могут сильно маскировать «полезные» вариации величин (6) внутри интервала. Поэтому перед
вычислением непрерывного вейвлет-преобразования рекомендуется избавляться от низкочастотных
трендов и, кроме того, при интерпретации непрерывных вейвлет-диаграмм вводить поправки на то,
что значения | Wx(t , a) | для моментов времени t , близких к началу и концу интервала задания
сигнала, на самом деле не отражают истинных свойств сигнала. Для данного масштаба a длина
«мертвых» отрезков времени, примыкающих к концам выборки обычно пропорциональна масштабу.
Для используемых ниже вейвлетов, скорость затухания которых задается множителем в виде
гауссовской функции, эту длину можно положить равной 3a .
Одной из наиболее популярных функций (t ) является т.н. вейвлет Морле (Morlet) или
комплекснозначный «модулированный гауссиан»:
(t )
1
1/ 4
exp(t 2 / 2 i t ) .
(7)
Этот вейвлет наилучшим образом приспособлен для выделения короткоживущих
гармонических всплесков (цугов) и обладает определенными свойствами оптимальности в поиске
компромисса между частотным и временным разрешением (выходит на т.н. гейзенберговский
предел).
Другим популярным семейством функций (t ) являются т.н. гауссовские вейвлеты,
определяемые как производные от гауссиана заданного порядка m :
m (t ) cm
2
d m t 2
e (1)m cm H m (t )e t , m 1 ,
m
dt
(8)
где cm – нормировочные константы, обеспечивающие единичную квадратичную интегральную
норму для (t ) , H m (t ) – полиномы Эрмита, H 0 (t ) 1, H1 (t ) 2t , H m1 (t ) 2tH m (t ) 2mH m1 (t ) .
Из них наиболее известна «мексиканская шляпа» 2 (t ) . Для данного порядка m функция (8)
обладает свойством обнуления первых m моментов:
t
k
m
(t )dt 0, k 0,1,..., (m 1) .
(9)
Отсюда следует, что если x( s) – полином порядка не выше m 1 включительно, то его
преобразование (6) будет тождественно равным нулю. Форма вейвлета 2 (t ) ориентирована на
выделение симметричных всплесков «классической» неосциллирующей формы. Более
содержательная интерпретация непрерывных вейвлет-диаграмм для семейства (8) дается с помощью
цепей скелета максимумов модулей величин | Wx(t , a) | или так называемый WTMM-анализ
[Любушин, 2007; Mallat, 1998], однако его изложение выходит за рамки данных лекций.
На рис. 3, а представлен график непрерывной записи сейсмического шума на широкополосной
станции длительностью 1 год поле перехода к шагу по времени 1 час путем вычисления
последовательных средних значений шума. На рис. 3, б представлена вейвлет-диаграмма Морле
(логарифм квадратов вейвлет-коэффициентов Морле) этого временного ряда, на которой видны
модуляции 12 и 24-часовых приливных гармоник 28-суточным периодом лунного месяца.
3000
(а)
2000
1000
0
-1000
-2000
Время, часы
-3000
0
1000
2000
3000
4000
5000
6000
7000
8000
Рис. 3. Временной ряд средних часовых значений непрерывных записей сейсмического шума на
широкополосной станции и его диаграмма Морле
ОРТОГОНАЛЬНЫЕ ВЕЙВЛЕТ-РАЗЛОЖЕНИЯ
Ортогональный кратно-разрешающий анализ (вейвлет-разложение) сигнала x( s)
непрерывного аргумента s определяется формулой [Daubechies, 1992; Chui, 1992; Mallat, 1998]:
x( s )
x ( ) ( s),
x ( ) ( s)
Здесь
b ( ) (s ) ,
( )
j
( )
j
( )
( )
j
(j ) j 2 .
(10)
является номером уровня детальности,
b(j ) b( ) ( (j ) )
x(s)
( )
( s (j ) ) ds
(11)
от
-ом уровне детальности, соответствующие моменту времени (j ) ,
( ) ( s) являются базисными функциями -ого уровня, которые получаются путем растяжения и
вейвлет-коэффициенты на
переноса основной вейвлет-функции ( s) :
( ) (s) ( 2) (2 s),
( ) ( s (j ) ) ( 2) (2 s j) .
(12)
Функция ( s) конструируется таким образом, чтобы она была финитной, имела единичную
среднеквадратичную норму и бесконечное множество функций {
( )
( s (j ) ) }, сдвинутых в точки
(j ) и растянутых (или сжатых) в 2 раз копий основной функции, образовывали бы
ортонормальный базис в L2 (, ) . Например, если:
( s) = 1 для s (0, 12 ]
(13)
+1 для s ( 12 ,1] и ноль для прочих t .
тогда формула (10) соответствует разложению функции x( s) по вейвлетам Хаара. Функция (13)
является простейшим и наиболее компактным ортогональным финитным вейвлетом. Наиболее
популярным семейством ортогональных вейвлет-функций являются функции Добеши (Daubechies)
(s) D2 p ( s) порядка 2 p , которые обладают следующими свойствами:
D2 p ( s) 0 вне интервала [ p 1, p] ,
(14a)
s
k
D2 p ( s) ds 0
для k 0,...,( p 1)
(14b)
С ростом числа p обнуляемых моментов в формуле (14b) функция D2 p ( s) становится все
более гладкой, хотя число ее непрерывных производных не является пропорциональным параметру
p . Например, функция Добеши 4-го порядка D2 p ( s) обнуляет нулевой и первый момент и
непрерывно дифференцируема во всех точках, за исключением счетного множества точек вида k 2l
для целых чисел k , l . В точках такого вида D4 ( s) имеет левостороннюю производную, но не имеет
правосторонней. Отметим, что вейвлет Хаара (13) является вейвлетом Добеши 2-го порядка ( p 1 ).
Мы использовали словарь из 17 вейвлетов: 10 обычных ортогональных вейвлетов Добеши с
порядками от 2 до 20 (использование более высоких порядков сопряжено с численной
неустойчивостью) и 7 т.н. «симлетов» - модификаций вейвлетов Добеши, в которых форма базисных
функций является более симметричной, чем для обычных вейвлетов [Daubechies, 1992; Chui, 1992;
Mallat, 1998]. Симлеты обладают теми же свойствами компактности, ортогональности, полноты и
гладкости, что и вейвлеты (14), но для порядков от 2-го до 6-го они совпадают с обычным
ортогональным базисом Добеши, а затем, для порядков от 8-го до 20-го, появляются различия в
форме базисной функции. Вследствие этого, общее число используемых нами вариантов
ортогональных компактных базисных функций равно 17.
Рассмотрим ситуацию, когда z (t ) представляет собой сигнал с дискретным временем t длиной
N отсчетов, t 1,..., N . Будем считать, что N имеет вид целого числа вида 2m - это удобно для
последующего использования быстрого вейвлет-преобразования. Если N не равно 2m , то дополним
сигнал z (t ) нулями до длины, которая будет равна 2m , где m минимальное целое число, для
которого N 2m . Формула кратно-разрешающего анализа в случае конечной выборки и дискретного
времени:
z (t ) a
где z
( )
( m)
1
m
z
1
( )
(t ),
z
( )
(t )
2( m )
c ( ) (t ),
( )
j 1
( )
j
( )
( )
j
(j ) j 2 ,
(15)
(t ) является компонентой сигнала, принадлежащей уровню детальности с номером , a (1m ) -
константа, пропорциональная среднему значению выборки [Daubechies, 1992; Chui, 1992; Mallat,
( )
( )
( )
1998; Press et al, 1996b]. В формуле (15) коэффициенты c j c ( j ) могут быть представлены,
подобно формуле (11), в виде свертки базисной функции
некоторым сигналом z ( s) :
c
( )
j
z (s)
( )
( )
( s) от непрерывного аргумента s с
( s (j ) ) ds .
(16)
Сигнал z ( s) от непрерывного аргумента s получается из сигнала z (t ) с дискретным временем
t путем интерполяции по формуле:
z ( s) z (t ) ( s t ) ,
(17)
t
где функция ( s) носит название масштабирующей функции вейвлет-разложения. Например, для
вейвлета Хаара ( s) 1 для s [0,1] и ( s) 0 для всех прочих s и, следовательно,
интерполированный сигнал будет кусочно-постоянной функцией. В общем случае ортогональных
вейвлетов Добеши масштабирующая функция является ортогональной основной базисной функции
( s) :
(s) (s) ds 0 и имеет те же свойства гладкости и компактный носитель той же длины,
что и ( s) (но не совпадающий полностью с ним): ( s) 0 вне интервала [0, 2 p 1] .
Если дискретный сигнал z (t ) получается из сигнала с непрерывным временем x( s) путем
взятия отсчетов с шагом s по времени, то при стремлении s 0 интерполированный сигнал
z ( s) всегда стремится в среднеквадратической метрике к исходному x( s) . Если в формуле (17)
используется масштабирующая функция ( s) , соответствующая базису Добеши порядка 2 p , то
интерполированный сигнал z ( s) будет иметь ( p 1) первых производных, непрерывных почти
всюду, за исключением, возможно, счетного числа точек, независимо от гладкости исходного сигнала
x( s) . Но при стремлении s 0 эти производные будут стремиться в интегральной метрике к
производным исходного сигнала лишь в том случае, если x( s) будет также ( p 1) раз
дифференцируем почти всюду. Таким образом, выбор вейвлета для анализа сигнала должен
соответствовать его гладкости.
Если забыть о возможном происхождении сигнала z (t ) в результате дискретизации
( )
непрерывного сигнала x( s) с некоторым шагом по времени s , то коэффициенты c j дискретного
разложения (16) являются результатом применения последовательной линейной фильтрации
дискретного сигнала. На первом шаге происходит разделение дискретного сигнала на 2 части:
(1)
вейвлет-коэффициенты 1-го уровня детальности c j (или «детальный сигнал» 1-го уровня) и т.н.
(1)
аппроксимирующий (сглаженный) сигнал a j 1-го уровня по формуле:
(0)
(0)
c(1)
a (1)
a (0)
j g (t 2 j ) a t ,
j h(t 2 j ) a t ,
t z (t ),
t
j 1,..., N / 2 .
(18)
t
Коэффициенты линейного фильтра g (k ) в формуле (18) обладают свойством выделения
высоких частот, а коэффициенты h(k ) – свойством сглаживания. Отметим, что формулы (18)
включают в себя не только линейную фильтрацию, но и прореживание в 2 раза – поэтому детальный
и аппроксимирующий сигналы содержат в 2 раза меньше отсчетов, чем исходный. Из-за конечной
длины выборки при применении формул (18) возникают технические сложности в начале и в конце
выборки. Существуют различные приемы преодоления этих трудностей, например, рассмотрение
выборки z (t ) на кольце вместо интервала. При этом могут возникать краевые искажения результатов
вейвлетной фильтрации, аналогичные краевым искажениям из-за циклического эффекта дискретного
преобразования Фурье [15]. После первого шага (18) он повторяется еще (m 1) раз (напомним что
N 2m ):
c( j 1) g (t 2 j ) at( ) , a ( j 1) h(t 2 j ) at( ) ,
t
j 1,..., N 2( 1) .
(19)
t
Таким образом, согласно формуле (19), на каждом новом уровне детальности вейвлет( )
разложения происходит однотипное расщепление аппроксимирующего сигнала a j предыдущего
уровня детальности на его высокочастотную составляющую c ( j 1) и на «еще более сглаженный»
( 1)
сигнал a j . Число отсчетов в детальном сигнале (то есть число вейвлет-коэффициентов) и в
сглаженном (аппроксимирующем) сигнале всякий раз уменьшается в 2 раза при увеличении номера
(m)
уровня детальности на единицу. Коэффициент a 1 в формуле (15) является аппроксимирующим
«сигналом», соответствующим самому глубокому сглаживанию на последнем уровне детальности m
. Коэффициенты g (k ) и h(k ) линейных фильтров (имеющих название «сопряженных зеркальных
1 k
фильтров») связаны друг с другом соотношением g (k ) (1) h(1 k ) , которое вытекает из
масштабирующих уравнений ортогонального кратно-разрешающего анализа:
1
(t / 2)
2
h(k ) (t k ),
k
1
(t / 2)
2
g (k ) (t k )
(20)
k
для масштабирующей и основной базисной функций. Для финитных базисных функций Добеши
D2 p ( s) число ненулевых коэффициентов в линейных зеркальных фильтрах g (k ) и h(k ) равно
порядку функции 2 p . Например, для вейвлета Хаара h(k ) 1/ 2 для k 0,1 и h(k ) 0 для всех
прочих k . Для функций Добеши 4-го и 6-го порядков коэффициенты зеркальных фильтров находятся
аналитически из линейных уравнений, вытекающих из условия (14b) обнуления заданного числа
первых моментов, но для более высоких порядков эти линейные уравнения решаются уже численно.
Следует заметить, что с ростом порядка вейвлета обусловленность линейных уравнений уменьшается
и растет ошибка округления. Поэтому обычно ограничиваются вейвлетами до 20-го порядка.
Алгоритмически
вейвлет-преобразование
является
линейным
ортогональным
преобразованием N мерного
вектора
выборки
в
вектор
коэффициентов
z (t )
Cz( N ) (a(1m) , c(1m) ,...,(c(j ) , j 1,..., n ),...) , длина которого также равна N и который состоит из
(m)
постоянной a 1 на первом месте и последовательно состыкованных друг с другом коэффициентов
всех уровней детальности, начиная с m го, (m 1) го и так далее, вплоть до коэффициентов
первого уровня детальности, занимающего всю вторую половину вектора Cz( N ) [Press et al, 1996b].
Рис.4 иллюстрирует эту последовательность. Обратное преобразование вектора Cz( N ) дает исходную
выборку z (t ) . Заметим, что обратное вейвлет-преобразование осуществляется также в виде
последовательных шагов восстановления аппроксимирующего сигнала уровня из вейвлет( 1)
( 1)
коэффициентов c k
и аппроксимирующего сигнала a k
уровня ( 1) с использованием
зеркальных сопряженных фильтров по формуле:
a(j ) h( j 2k ) a ( k 1) g ( j 2k ) c ( k 1) ,
k
j 1,..., N 2 .
k
Исходный сигнал x(t), t0,1,...,(N-1), N 2 m
Дискретное вейвлет-преобразование
Вейвлет-коэффициенты
2-го уровня детальности
Число коэффициентов = N / 4
4t Периоды 8t
Вейвлет-коэффициенты
3-го уровня детальности
Число коэффициентов = N / 8
8t Периоды 16t
Вейвлет-коэффициенты
4-го уровня детальности
Число коэффициентов = N / 16
16t Периоды 32t
Рис. 4. Иллюстрация дискретного вейвлет-преобразования
Вейвлет-коэффициенты
1-го уровня детальности
Число коэффициентов = N / 2
2t Периоды 4t
(21)
Обратное преобразование начинается с коэффициентов a (1m ) и c (1m ) последнего (самого
низкочастотного) уровня детальности с номером m и заканчивается на 1-ом уровне. При этом
происходит увеличение в 2 раза числа отсчетов в аппроксимирующем сигнале каждый раз при
уменьшении номера уровня детальности – до тех пор, пока последовательность восстановлений не
остановится на 1-ом уровне детальности и число отсчетов не станет равным N . Прямое и обратное
вейвлет-преобразования (19) и (21) допускают программную реализацию в виде быстрых алгоритмов,
требующих O( N ) операций, что по скорости превосходит быстрое преобразование Фурье
[[Daubechies, 1992; Chui, 1992; Mallat, 1998; Press et al, 1996b]. Компонента z
( )
(t ) является
результатом обратного преобразования вектора коэффициентов типа Cz( N ) , при условии обнуления
всех коэффициентов, кроме соответствующих уровню .
Компонента z
( )
(t ) для достаточно большого значения N частотно локализована в полосе:
)
)
[(min
, (max
] [1/(2( 1) s),1/(2 s)] ,
(22)
( )
где s – длина интервала опроса. Значение коэффициента c j отражает поведение сигнала z (t ) в
( )
окрестности точки j на интервале длиной p 2
отсчетов. Следовательно, чем более гладким
является вейвлет, тем шире этот интервал. Однако основные вариации (всплески) финитной базисной
( )
функции ( s) всегда сосредоточены на интервале длиной 2 независимо от параметра гладкости
p . Поэтому каждому коэффициенту c (j ) припишем «временную зону ответственности» длиной
T ( ) s 2 . Произведение ширины ( ) 1/(2 1 s) частотной полосы (22) на длину
( )
временного интервала T
задает площадь так называемых «ящиков Гейзенберга» на плоскости
«время-частота», которая равна ½ независимо от рассматриваемого уровня детальности.
Самым мелкомасштабным уровнем детальности в формуле (15) является первый, общее число
( )
(m)
уровней детальности m зависит от длины выборки. Совокупность значений c j и a 1 вычисляются
путем прямого быстрого вейвлет-преобразования [[Daubechies, 1992; Chui, 1992; Mallat, 1998; Press et
al, 1996b]. Они однозначно определяют исходную выборку z (t ) , которая может быть восстановлена
( )
(m)
по заданным c j и a 1 путем обратного быстрого вейвлет-преобразования. Уровень детальности
можно ассоциировать с номером частоты (частотным дискретом) в классическом дискретном Фурьепреобразовании. Отличие вейвлет-разложения состоит в том, что набор “вейвлет-частот” значительно
более редок (равномерен в логарифмической шкале), чем в Фурье-анализе. Это является платой за
важное свойство – финитность базисных функций, которое отсутствует в Фурье-разложении и
которое позволяет гораздо более точно определять местоположения короткоживущих аномалий всплесков. Кроме того, финитность базисных функций позволяет производить вейвлет-анализ
нестационарных и негауссовых временных рядов, Фурье-анализ которых хотя формально и
возможен, однако малоэффективен.
Хотя обычное вейвлет-разложение обладает полезным свойствами высокой точности
локализации по времени нестационарных сигналов, оборотной стороной этого свойства, в
соответствии с принципом Гейзенберга, является слабое разрешение по частоте. Вейвлет-пакетное
разложение позволяет частично устранить этот недостаток за счет некоторого ухудшения разрешения
по времени. Реализация пакетного расщепления основана на иерархической схеме последовательных
( )
вейвлет-преобразований исходных коэффициентов c j . Ортогональное вейвлет-пакетное
разложение сигнала, аналогично формуле (15), может быть записано в виде суммы:
z (t ) a
(m)
1
m
mq 1
z
( )
mq
q
(t ) z ( , ) (t ) .
(23)
1 1
Величина q может быть равна 2, 4, 8, …, то есть имеет вид q 2 , r 1, 2,3,... и определяет
число подуровней, на которое расщепляется обычный уровень детальности. Для заданного значения
параметра q максимальный номер mq m уровня детальности , который может быть расщеплен,
r
определяется из условия, что он должен содержать минимум q вейвлет-коэффициентов. Компоненты
z ( , ) (t ) частотно-упорядочены, расщепляют частотную полосу (22), соответствующую уровню
( , )
(t ) частотно-локализован в полосе:
детальности на q равных частей. Таким образом, сигнал z
( , )
( , )
( , )
( )
( )
[min , max ] , min min ( 1) , 1,..., q;
(24)
, )
, )
)
)
(max
(min
( ) , ( ) ((max
(min
)/q
Если уровню детальности с номером соответствует n обычных вейвлет-коэффициентов, то
каждому
подуровню
пакетного
разложения
соответствует
вейвлет-пакетных
n / q
( , )
коэффициентов c j , j 1,..., n / q , «ящики Гейзенберга» для которых имеют временную длину в
q раз большую, что исходные коэффициенты c (j ) , но их частотная сторона в q раз меньше
(следовательно, площадь «ящиков Гейзенберга» остается неизменной и равной ½).
Рис. 5. Ортогональные вейвлет-пакетные разложения сейсмической записи.
Рост номеров уровней и подуровней (и увеличение характерных периодов) происходит сверху-вниз
Для того чтобы получить компоненту z
вейвлет-преобразований коэффициентов
c
( , )
( , )
j
(t ) , необходимо совершить цепочку обратных
. Последний шаг в этой цепочке обратных
( , )
преобразований совершается от некоторого набора коэффициентов w j , j 1,..., n , которые
( )
занимают в аналоге вектора Cz( N ) те же позиции, что и обычные коэффициенты c j разложения
сигнала z (t ) . Однако обратное преобразование от них дает компоненту z
( , )
(t ) , а не z ( ) (t ) .
( , )
Назовем коэффициенты w j
модифицированными вейвлет-пакетными коэффициентами сигнала
z (t ) . Таким образом, модифицированные коэффициенты w(j , ) являются обычными вейвлет-
коэффициентами на уровне детальности для случая, когда на вход прямого преобразования
z ( , ) (t ) . Ящики Гейзенберга для
( )
имеют ту же временную длину, что и для c j , но их частотная длина равна
подается не исходный сигнал, а лишь его компонента
( , )
коэффициентов w j
( , )
частотной длине коэффициентов c j . Таким образом, переход от обычных вейвлет-пакетных
( , )
коэффициентов c j
( , )
к модифицированным w j
является приемом, позволяющим сузить
временной интервал неопределенности (уменьшить временную длину ящика Гейзенберга). Заметим,
n
что при таком переходе энергия коэффициентов разложения сохраняется:
(w(j , ) )2
j 1
n / q
(c )
j 1
( , ) 2
j
.
Рис. 6. Ящики Гейзенберга и вейвлет-диаграмма Морле для сейсмической записи на рис. 5. По горизонтальной
оси отложено время в секундах, по вертикальной оси – логарифм периода в сек, но метки даны в секундах.
Копии экрана из пакета Spectra_Analyzer
Если на плоскости «время-частота» построить 2-мерную карту, состоящую из частотно( , )
упорядоченных ящиков Гейзенберга модифицированных коэффициентов w j
и закрасить каждый
ящик в соответствии с палитрой, пропорциональной абсолютным значениям вейвлет-пакетных
( , )
коэффициентов w j
(или их логарифмам), то получится диаграмма, визуализирующая временную
динамику основных временных масштабов (или периодов) нестационарного сигнала. Внешне эта
мозаика из вейвлет-пакетных ящиков Гейзенберга может проигрывать в эстетическом восприятии по
сравнению, например, с традиционными спектрально-временными диаграммами. Однако она дает
более точное и адекватное представление о частотно-временной динамике сильно нестационарного
сигнала, состоящего из множества короткоживущих всплесков различного масштаба, форма которых
может сильно отличаться от гармонического колебания той или иной частоты.
Одним из важных вопросов, который необходимо решать при применении ортогональных
вейвлет-разложений, является выбор наилучшего базиса, например, порядка вейвлета Добеши. При
выборе оптимального вейвлет-базиса наиболее часто используется критерий минимума энтропии
распределения квадратов модулей вейвлет-коэффициентов:
m 2( m )
E ( x )
1
j 1
p (j ) ln( p (j ) ) min,
p (j ) | c (j ) |2
|c
( ) 2
i
| .
(25)
,i
Метод (25) подбирает для сигнала z (t ) такой базис, в котором распределение значений
квадратов его вейвлет-коэффициентов максимально отличаются от равномерного. Тем самым
максимум информации сосредотачивается в минимальном количестве коэффициентов разложения.
На рис. 5 приведен пример разложения сейсмической записи по первым 6 уровням детальности
вейвлет-разложения и вейвлет-пакетные разложения с расщеплением уровней детальности в 2 и 4
раза. Использовался вейлет Добеши с 10 обнуляемыми моментами, который найден из критерия (25).
На рис. 6 представлены для сравнения частотно-временные диаграммы ящиков Гейзенберга (с
расщеплением 10 уровней детальности на 8 подуровней) и Морле для этой сейсмической записи.
Использование вейвлет-пакетов позволяет получить оценку так называемого вейвлет-пакетного
( , ) 2
спектра мощности как последовательности квадратов вейвлет-пакетных коэффициентов | c j | в
зависимости от центральной частоты полосы (24). Такой спектр мощности проигрывает
классическим оценкам спектра мощности по частотному разрешению, но обладает положительным
свойством хорошего сглаживания статистических флуктуаций спектра мощности.
Вейвлет-пакетные спектры мощности:
Черная линия - без расщепления уровней
Синяя линия - расщепление уровней в 2 раза.
Фиолетовая линия - расщепление уровней в 4 раза.
Красная линия - расщепление уровней в 8 раз.
0.001
Оценка спектра мощности путем усреднения AR(204)-оценок
в последовательных окнах длиной 2048 отчетов
0.001
0.0001
0.0001
1E-005
1E-005
1E-006
1E-006
1E-007
1E-007
1E-008
1E-008
1E-009
1E-009
1E-010
1E-010
1E-011
1E-011
1E-012
1E-012
1E-013
1E-013
1E-014
1E-014
1E-015
1E-015
1E-016
1E-016
1E-017
1E-017
10
100
1000
Временные масштабы (периоды), сек, соответствующие центрам
частотных полос уровней и подуровней вейвлет-пакетных разложений.
10
100
1000
Периоды, сек
Рис. 7. Вейвлет-пакетные спектры мощности в сравнении с авторегрессионной оценкой для сейсмической
записи на рис. 5
На рис. 7 представлены графики семейства вейвлет-пакетных спектров мощности для
различного расщепления уровней детальности в сравнении с классической авторегрессионной
оценкой. Заметим, что с ростом кратности расщепления уровней значения вейвлет-пакетных
спектров мощности уменьшаются – это естественно, поскольку монотонно уменьшается ширина
частотной полосы, приходящейся на один вейвлет-пакетный коэффициент.
После определения для данного сигнала оптимального вейвлет-базиса может быть найдена та
часть минимальных по модулю вейвлет-коэффициентов, которая может быть отброшена при
обратном вейвлет-преобразовании, поскольку она отвечает шуму. Для этого делается предположение,
что шум в основном сосредоточен в вариациях на первом, самом высокочастотном уровне
детальности, за исключением небольшого числа точек, в котором сконцентрированы
высокочастотные особенности поведения полезного сигнала и которым, следовательно,
соответствуют большие значения вейвлет-коэффициентов 1-го уровня. В силу ортогональности
вейлет-преобразования дисперсия вейвлет-коэффициетов равна дисперсии исходного сигнала.
Поэтому оценим стандартное отклонение шума для вейвлет-коэффициентов на 1-м уровне
детальности. При этом следует учесть, что оценка должна быть робастной, нечувствительной к
возможным большим выбросам «полезных» значений вейвлет-коэффициентов на 1-м уровне.
Например, можно использовать робастную медианную оценку стандартного отклонения для
нормальной случайной величины [Huber, 1981]:
med{| c(1)
j | , j 1,..., N / 2}/ 0.6745 .
(26)
Теперь, зная оценку , можно оценить, порог тех значений модуля вейвлет-коэффициентов,
ниже которого их можно обнулить, поскольку они являются носителями шумовых вариаций. Для
вывода значения этого порога используется формула асимптотического максимального уклонения
гауссовского белого шума, в результате применения которой порог получается равным 2 ln N
[Mallat, 1998]. Отсюда очевидно определяется уровень Донохо-Джонстона [17] для сжатия
( )
сигнала: отношение числа коэффициентов, для которых выполнено условие | c j
| 2 ln N , к
общему их числу N . Эта безразмерная величина , 0 1, может быть использована в
дальнейшем как интегральная характеристика сигнала, например, для решения задач классификации.
Более распространенным применением порога Донохо-Джонстона является операция
нелинейной пороговой фильтрации (thresholding) сигнала, которая заключается в выполнении
следующей последовательности операций:
1) для выбранного ортогонального вейвлет-базиса совершить прямое дискретное вейвлетпреобразование;
2) отсортировать вейвлет-коэффициенты, не различая уровней детальности, в порядке
возрастания их абсолютных величин;
3) положить равными нулю заданную часть коэффициентов, минимальных по модулю
(таким образом, отличными от нуля остаются лишь доля 1 коэффициентов, имеющих
наибольшие абсолютные значения);
4) совершить обратное дискретное вейвлет-преобразование.
Результатом будет некоторый сигнал zT (t ) , который сохранит лишь наиболее значимые
вариации исходного сигнала z (t ) , отобранные не по частотному принципу, а согласно критерию
наибольших значений вейвлет-коэффициентов.
Пусть z(t ) f (t ) W (t ) , где f (t ) - «полезный» сигнал, представляющий собой кусочнополиномиальную функцию, а W (t ) - гауссовский белый шум с дисперсией 2 . Таким образом,
интервал отсчетов t 1,..., N , на которых задан f (t ) , разбит на конечное число (не зависящее от N )
непересекающихся сегментов, на каждом из которых полезный сигнал равен полиному той или иной
степени, а на граничных точках сегментов сам сигнал или его производные могут претерпевать
разрывы. Пусть m - максимальная степень полиномов, а K - общее число точек разрыва f (t ) .
Пусть zT (t ) - сигнал, полученный из z (t ) операцией нелинейной пороговой фильтрации с
использованием порога Донохо-Джонстона и ортогонального вейвлета, обнуляющего (m 1)
моментов. Тогда справедлива оценка [Mallat, 1998; Donoho, Johnstone, 1994]:
M {|| zT f ||2 } ( K 1)(m 1) C ln 2 ( N )
0,
N
|| f ||2
2
N
где M {...} – знак математического ожидания, || f ||2
(27)
N
f
2
(t ) , C 4 / ln(2) - некоторая константа,
t 1
2 || f ||2 / 2 - отношение «сигнал/шум».
0
-10000
-20000
-30000
-40000
Время, минуты
-50000
0
5000
10000
15000
20000
Рис. 8. Результат пороговой вейвлет-фильтрации сейсмической записи из рис.2. Обнулено 99% вейвлеткоэффициентов ( 0.99 )
На рис. 8 представлен результат пороговой вейвлет-фильтрации сейсмической записи из рис.2.
Оптимальный вейвлет для нее был определен D8 , то есть вейвлет Добеши, обнуляющий 4 момента.
Порог Донохо-Джонстона 0.83 , то есть можно оставить лишь 17% вейвлет-коэффициентов,
обнулив остальные. Однако при таком пороге исходная запись визуально неотличима от той, которая
получается после пороговой фильтрации. Поэтому положим 0.99 , то есть оставим ненулевыми
лишь 1% коэффициентов. Результат такой фильтрации представлен на рис.8, где серой линией
изображена исходная запись, а синей – результат фильтрации. Видно, что результат фильтрации
можно представить как сумму 2-х составляющих – плавной, напоминающей тренды на рис.2 и
высокочастотные всплески на тех фрагментах, где вейвлет-коэффициенты младших уровней
детальности недостаточно малы, чтобы быть обнуленными.
МУЛЬТИ-ФРАКТАЛЬНЫЙ АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Анализ фрактальных и мультифрактальных свойств временных рядов мониторинга является
одним из перспективных направлений анализа данных в физике твердой Земли, метеорологии,
гидрологии. Это обусловлено способностью фрактального анализа исследовать сигналы, которые с
точки зрения ковариационной и спектральной теории являются не более чем белым шумом либо
броуновским движением. Одной из первых работ по анализу фрактальных свойств временных рядов
являются работы американского гидролога Херста по исследованию среднегодового режима расхода
воды в реках [Hurst, 1951; Mandelbrot, Wallis, 1969; Feder, 1988]. Эмпирический закон Херста
H
заключается в выполнении соотношения: R( ) / ( ) , где R( ) - разница между
максимальными и минимальными значениями приращений наблюдаемой величины на временном
интервале длиной , ( ) - стандартное отклонение, 0 H 1 - постоянная, значение которой для
большинства метеорологических и гидрологических наблюдений лежит в окрестности 0.7. Для
самоподобного
процесса
среднее
значений
квадрата
приращений
x(t )
M {| x(t t ) x(t ) |2} | t |2 H , а зависимость спектра мощности от частоты носит степенной
(2 H 1)
, 0.
характер S xx ( )
Дальнейшее обобщение этой модели состоит в допущении зависимости постоянной Херста от
времени,
то
есть
в
рассмотрении
такого
случайного
процесса,
для
которого
2
2 H (t )
M {| x(t t ) x(t ) | } | t |
, 0 H (t ) 1 . Это обобщение было предложено Мандельбротом
[19,20] и названо мультифрактальным броуновским движением, которое описывается плотностью
распределения вероятности тех или иных значений H (t ) т.н. мультифрактальным спектром
сингулярности. Спектр сингулярности представляет собой информативную статистику,
характеризующую режим хаотических флуктуаций наблюдаемой величины.
Мера изменчивости случайного сигнала
на интервале времени [ t , t + ]
Мультифрактальный спектр сингулярности F()
и его параметры: - ширина носителя и
- обобщенный показатель Херста.
F() - фрактальная размерность множества
моментов времени t, для которых h(t) =
1.0
0.8
X(t, ) h(t)
0.6
0.4
max min
0.2
t
0.0
0.05
min
0.10
max
0.15
Рис. 9. Иллюстрации к понятию мульти-фрактального спектра сингулярности
0.20
0.25
0.30
0.35
Рисунок 9 иллюстрирует понятие спектра сингулярности. Рассмотрим некоторое случайное
колебание x(t ) на интервале времени [t , t ] и размах x (t , ) случайного колебания на данном
интервале, т.е. разницу между максимальным и минимальным значениями (левая часть рис. 9). Если
устремить 0, то x (t , ) будет также стремиться к нулю, но здесь важна скорость убывания.
Если скорость определяется законом
h (t )
:
x (t , )
0
h (t ) или если существует предел
h(t ) lim log( x (t , )) log( ) , то величина h(t) называется экспонентой Гельдера – Липшица.
0
Если величина h(t ) не зависит от момента времени t : h(t ) const H , то случайное колебание
x(t ) называется моно-фрактальным, а величина H — постоянной (или экспонентой) Херста. Если
экспоненты Гельдера – Липшица существенно различаются для разных моментов времени, то
случайное колебание называется мульти-фракталом и для него можно определить понятие спектра
сингулярности F ( ) (правая часть рис. 9). Мысленно выделим множество C ( ) таких моментов
времени t , которые имеют одно и то же значение экспоненты Гельдера – Липшица: h(t ) .
Множества C ( ) существуют (содержат какие-то элементы) не для всех значений , т.е.
существуют некоторые минимальное min и максимальное max и лишь для min max
множества C ( ) будут непустыми. Для каждого значения в интервале между минимальным и
максимальным значениями множество C ( ) состоит из точек, довольно причудливо разбросанных
по временной оси. Размерность временной оси, которую в данном случае можно назвать множеством,
вмещающим в себя множества C ( ) , равна 1. Но размерность множеств C ( ) меньше единицы —
они фрактальны.
В настоящее время существуют 2 подхода для оценки спектров сингулярности временного
ряда. Первый метод появился раньше и основан на анализе цепей точек максимума модулей
непрерывных вейвлет-преобразований с вейвлетами, обычно равными производной той или иной
степени от функции плотности распределения Гаусса [Mallat, 1998]. Второй подход более близок к
технике Херста и основан на анализе зависимости стандартного отклонения или размаха выборки от
ее длины. В последнее время был разработан и активно применяется в различных приложениях метод
анализа флуктуаций после исключения масштабно-зависимых трендов – Detrended Fluctuation
Analysis (DFA) [Kantelhardt et al, 2002]. Сравнительный опыт применения методов показывает, что
метод DFA является более надежным и устойчивым. Ниже будет использован только DFA и кратко
приведены основные конструкции метода.
Вычислим среднее значение меры x (t , ) в степени q :
M ( , q) M {(x (t , ))q } .
Случайный процесс называется масштабно-инвариантным, если M ( , q)
то есть существует предел:
(q) lim
0
ln M ( , q)
.
ln
(28)
(q)
при 0 ,
(29)
Согласно определению
x (t , ) max x(u) min x(u)
t u t
t u t
(30)
Если зависимость (q) является линейной: (q) Hq , где H const , 0 H 1 , то процесс
моно-фрактален. В частности, для классического броуновского движения H 0.5 . Возведение в
степень q подчеркивает различные типы поведения сигнала: если q 0 , то в значение меры (28)
основной вклад вносят интервалы времени с большими отклонениями от тренда, а если q 0 , то
интервалы времени с малыми вариациями.
Для вычисления функции (q) по конечной выборке из временного ряда x(t ), t 1,..., N
применим метод DFA [Kantelhardt et al, 2002]. Пусть s - число отсчетов, ассоциированное с
варьируемым масштабом s : s st . Разобьем выборку на непересекающиеся малые интервалы
длиной s отсчетов:
I k( s ) {t :1 (k 1)s t ks, k 1,...,[ N / s]}
(31)
и пусть
yk( s ) (t ) x((k 1)s t ), t 1,..., s
(32)
(s)
( s , m)
участок временного ряда x(t ) , соответствующий интервалу I k . Пусть p k (t ) - полином порядка
m , подогнанный методом наименьших квадратов к сигналу yk( s ) (t ) . Рассмотрим отклонения от
локального тренда:
y (ks ,m) (t ) yk( s ) (t ) p(ks , m) (t ), t 1,..., s
(33)
и вычислим значение:
Z
(m)
1/ q
[ N / s]
(q, s) (max y (ks ,m ) (t ) min y (ks ,m ) (t )) q
1t s
k 1 1t s
[ N / s]
(34)
,
которое будем рассматривать как оценку для ( M ( s , q)) . Процедура устранения тренда на каждом
малом участке длиной s отсчетов необходима в случае наличия в сигнале трендов внешнего
происхождения (сезонных, приливных и т.п.). Определим теперь функцию h(q) как коэффициент
1/ q
( m)
( m)
линейной регрессии между значениями ln( Z (q, s)) и ln( s) : Z (q, s)
(q) qh(q) , а для моно-фрактального процесса h(q) H const .
Следующий шаг состоит в вычислении статистической суммы Гиббса:
W ( q, s )
[ N / s]
(max y
k 1
1t s
( s ,m)
k
(t ) min y (ks ,m) (t )) q
(35)
1t s
и определения показателя массы (q) из условия W (q, s)
вычисляется согласно формуле:
F ( ) max { min( q (q)), 0 }
q
s h ( q ) . Очевидно, что
s ( q ) , после чего спектр F ( )
(36)
.
Сравнивая (35) и (36), нетрудно заметить, что (q) (q) 1 qh(q) 1 . Таким образом,
F ( ) max { min(q( h(q)) 1, 0 } .
q
При вычислении величин и * использовались следующие соображения. Показатель
степени q варьировался внутри интервала: q [Q, Q] , где Q – некоторое достаточно большое
число, например Q 10 . Для каждого значения
внутри интервала [ Amin , Amax ] , где
d (q)
d (q)
, Amax max
, вычислялось значение F ( ) min ( q (q)) . Если
q[ Q , Q ] dq
q[ Q , Q ]
q[ Q , Q ] dq
Amin min
значение близко к Amin , то F ( ) 0 и эта величина не годится в качестве оценки спектра
сингулярности, который должен быть неотрицательным. Но, начиная с некоторого величина
F ( ) становится неотрицательной – это условие выделяет значение min . При дальнейшем
увеличении значение F ( ) увеличивается, достигает максимума при * , а затем начинает
уменьшаться и, наконец, достигает некоторого значения max Amax , такого, что при max оно
опять становится отрицательным: F ( ) 0 . Таким образом, F ( ) F ( ) при условии, что
F ( ) 0 , которое определяет интервал носителя спектра сингулярности [ min , max ] .
d (q )
Производная
находится численно по значениям (q), q [Q, Q] и при ее вычислении
dq
точность не имеет особого значения, так как она используется лишь для грубого определения
априорного интервала возможных показателей степени q .
Для моно-фрактального процесса, когда h(q) H const , получаем, что F ( H ) 1 и
F ( ) 0 H . В частности, положение и ширина носителя спектра F ( ) , то есть значения
min , max , max min и * - то значение, которое доставляет функции F ( ) максимум:
F ( * ) max F ( ) , являются характеристиками шума. Величину * можно назвать обобщенным
показателем Херста. Для моно-фрактального сигнала значение должно быть равно нулю, а
* H .
(а)
S
(б)
t
x(t,s)
1.2
(в)
F()
(г)
1.0
lg(Z(q,s))
F()
0.8
0.8
0.6
0.4
0.4
0.2
lg(s)
0.0
0
1.2
1.4
1.6
1.8
2
2.2
0.2
0.4
0.6
0.8
1.0
Рис. 10. Вычисление спектра сингулярности для временного ряда элетротеллурических потенциалов (шаг
по времени 1 час); (а), тонкая линия – фрагмент временного ряда; толстые линии – полиномиальные
тренды 4-го порядка, подогнанные внутри непересекающихся интервалов длиной s отсчетов; (б) –
разница внутри интервалов между исходными данными и трендами; (в) – графики зависимостей
lg(Z (q, s)) от lg( s) с подогнанными линейными трендами для последовательных значений степени q
(сверху вниз): 10, 7.5, 5, 2.5, -0.05, -2.5, -5, -7.5 и -10; (г) – спектр сингулярности
Рисунок 10 иллюстрирует последовательные этапы вычисления спектра сингулярности для
временного ряда электротеллурических потенциалов на Камчатке. На рис. 10, в представлены
( m)
графики как самих величин lg( Z (q, s)) , так и линейных трендов, подогнанных к ним для 10
различных значений степени q для того же временного окна. Наклон графиков линейных трендов
есть ничто иное, как функция h(q) , по значениям которой вычисляется показатель массы
(q) qh(q) 1 , а далее, согласно формуле (36), и сам спектр сингулярности.
(а)
0.5
(б)
0.4
0.3
0.2
0.1
1.6
(в)
1.2
0.8
0.4
0
0
20
40
60
Время, сутки от начала 01.07.2006
Рис. 11. Оценка эволюции мульти-фрактальных параметров и для сейсмической записи для одной
из широкополосных сейсмических станций сети F-net на Японских островах, для 2-месячного фрагмента
01.07-31.08.2006. Рис.(а) – сейсмическая запись после перехода к шагу по времени 1 минута, (б) и (в) –
оценки мульти-фрактальных параметров в последовательных интервалах длиной 1 сутки (1440 отсчетов)
*
Если оценивать спектр F ( ) в скользящем временном окне, то его эволюция может дать
информацию об изменении структуры хаотических пульсаций ряда. Обычно F ( ) 1 , но
*
встречаются окна, для которых F ( ) 1 . Напомним, что в общем случае (не только для анализа
*
временных рядов) величина F ( ) равна фрактальной размерности носителя мультифрактальной
меры [Feder, 1988].
*
Далее будут проанализированы временные ряды вариаций величин , , F ( ) для данных
мониторинга при их оценке в скользящем временном окне. Такой переход от исходных временных
рядов к характеристикам их мульти-фрактальных спектров сингулярности является важной
предварительно обработкой данных, освобождающих их от специфики, связанной с различной
физической природой, размерностью, масштабом измерений и, одновременно, выделяющих самые
общие свойства статистических флуктуаций. На рис. 11 представлены результаты перехода от
рассмотрения исходной сейсмической записи (вертикальных сейсмических колебаний) к анализу
временных рядов изменения их мульти-фрактальных характеристик [Любушин, 2009].
Заметим, что иногда интерес представляют лишь вариации показателя Херста. В этом случае он
может быть оценен непосредственно из определения показателя, данного самим Херстом
[Hurst, 1951; Mandelbrot, Wallis, 1969; Feder, 1988]. Пусть x(t ), t 1,..., N – анализируемый
временной ряд; L N – длина скользящего временного окна; - номер отсчета правого конца
скользящего окна, то есть мы рассматриваем моменты времени t , которые удовлетворяют условию
L 1 t . Пусть s - длина внутреннего временного окна, которое используется внутри
текущего основного окна для операций усреднения. Мы рассматриваем длины внутренних окон,
удовлетворяющие условию: s L / 5 . Пусть
*
*
1 s
x(u t 1)
s t 1
xs(,u)
(37)
выборочная оценка среднего значения на интервале длиной s отсчетов, который лежит внутри
текущего основного окна и начинается в точке u . Следующий шаг состоит в вычислении отклонений
от среднего значения (37), их накопленной суммы и размаха накопленной суммы:
xs(, u) (t ) x(t ) xs(,u) , s(,u) (t )
t
x
v 1
( )
s, u
(v), Rs(, u) max s(,u) (t ) min s(,u) (t )
t
t
(38)
для t [u, u s 1], u [ L 1, s 1] . Далее оцениваются дисперсия и среднее значение
отношения размаха к стандартному отклонению:
(
1 s
1
) (xs(, u) (t ))2 , RS ( ) ( s)
s t 1
( L s 1)
( ) 2
s, u
s 1
Rs(, u)
u L 1
s(, u)
.
(39)
Показатель Херста H ( ) в текущем временном окне оценивается как наклон кривой прямой
( )
линейной регрессии между значениями ln( RS ( s)) и ln( s) . Этот способ формально более прост,
чем метод DFA и требует меньших длин окон, однако он сильно подвержен наличию в сигнале
низкочастотных трендов, которые смещают оценку показателя Херста.
(2 H 1)
Для спектра самоподобного случайного процесса имеет место формула S xx ( )
при
0 [20]. Отсюда вытекает еще один способ оценки показателя Херста через наклон графика
логарифма спектра мощности в зависимости от логарифма частоты. Этот наклон ищется путем
подгонки линейного тренда в зависимости log( S xx ( )) от log( ) методом наименьших квадратов:
k
(log( S xx (k )) log(k ) ) 2 min , где k - значения частот, для которых был вычислен
( , )
спектр мощности, и последующего применения формулы H ( 1) / 2 .
Если использовать не обычные спектральные оценки, а разложения по вейвлетам, то оценку
постоянной Херста можно найти по скорости роста средних значений квадратов модулей вейвлеткоэффициентов:
W
N ( )
|c
j 1
( )
Здесь c j
| / N ( ) .
( ) 2
j
(40)
- коэффициенты ортогонального дискретного вейвлет-разложения выборки
самоподобного временного ряда, 1,..., m - номер уровня детальности разложения, N ( ) - число
вейвлет-коэффициентов на уровне детальности , N ( ) 2( m ) . Тогда, аналогично соотношению
2 H 1
для скорости роста спектра мощности, W ( s )
, где s - характерный временной масштаб
( 1)
уровня детальности . Поскольку s 2 2
, то отсюда следует, что
log 2 (W ) 2 H 1
(41)
Таким образом, значение коэффициента наклона прямой, подогнанной методом наименьших
квадратов к парам значений (log 2 (W ), ) , дает оценку для величины 2H 1 .
Сравним различные методы фрактального анализа временных рядов. На рис.12(а) представлен
график временного ряда наблюдений за вариациями электротеллурических потенциалов на Камчатке
[Любушин, Копылова, 2004]. Фрагмент этого временного ряда использовался в рис.10. Общая
продолжительность наблюдений составляет 4 года 8 месяцев (с 01.10.1996 по 23.06.2001), интервал
взятия отсчетов 1 час, общее число отсчетов N=41447. Рисунок 12, б представляет приращения
временного ряда на рис. 12, а.
40
0
(а)
-40
-80
(б)
10
0
-10
сутки
0
200
400
600
800
1000
1200
1400
1600
Рис. 12. Графики временного ряда электротеллурических потенциалов на Камчатке (а) и его приращений (б)
Рисунок 13 иллюстрирует три различных метода оценки постоянной Херста для временного
ряда, представленного на рис. 12. На рис. 13, а оценка получена как коэффициент наклона прямой
наилучшего приближения (штриховая линия) к графику логарифма оценки спектра мощности в
зависимости от логарифма периода. Оценка спектра мощности получена авторегрессионным
методом, как результат усреднения спектральных оценок в скользящем временном окне длиной 2048
отсчетов с использованием модели авторегрессии 200-го порядка внутри каждого окна. На графике
рис. 13, а видны спектральные пики, соответствующие 8, 12 и 24-часовым периодическим
компонентам. На рис. 13, б использована оценка (40)-(41), ортогональный вейвлет выбран из условия
минимума энтропии распределения квадратов вейвлет-коэффициентов (25) и им оказался вейвлет
Добеши 18-го порядка (обнуляющий 9 первых моментов). Наконец, рис. 13, в иллюстрирует
применение статистики (39).
1000
100
Sxx
20
(а), 2H + 1 = 1.67
15
10
5
log2 ( W )
(б), 2H + 1 = 1.80
4
ln ( RS )
(в), H = 0.46
10
3
1
5
2
0.1
Периоды, часы
0.01
1
10
100
1000
0
Номер уровня
2
4
6
8
10
12
ln ( s, сутки )
1
2
Рис. 13. Различные методы оценки показателя Херста для временного ряда на рис. 12, а
4
6
8
10
Эти методы дали значения постоянной Херста 0.37, 0.40 и 0.46. Различие в оценках не очень
существенно, но не пренебрежимо мало. Оценка на рис. 13, а представляется наименее надежной изза влияния монохроматических пиков.
Кроме того, следует учесть, что сигнал, возможно, является мультифракталом – в этом случае
отличия возникают просто вследствие различия методов и различий в «реакции» на них данных,
имеющих на самом деле иную природу. Для выяснения этого вопроса оценим спектр сингулярности
для приращений временного ряда (рис.12(б)) – см. рис. 14.
На рис. 14 представлены графики логарифмов
как самих величин (34), так и линейных трендов,
1.6
подогнанных к ним для 9 различных значений степени
lg(Z(q,s))
q . Наклон графиков линейных трендов есть функция
h(q) , по значениям которой вычисляется показатель
1.2
массы (q) , а далее и сам спектр сингулярности.
Рисунок 14 демонстрирует хорошее соответствие
( m)
линейному закону зависимости lg( Z (q, s)) от lg( s)
0.8
, то есть, самоподобность сигнала.
На рис. 14 приведены графики зависимостей с
подогнанными
линейными
трендами
для
0.4
последовательных значений степени q (сверху вниз):
10, 7.5, 5, 2.5, -0.05, -2.5, -5, -7.5 и -10. Масштаб s
изменялся, начиная с минимального значения 30
lg(s)
0
отсчетов (30 часов) – чтобы усреднить периодические
компоненты, максимальный период которых равен 24
1
1.5
2
2.5
3
3.5
4
часам. Следовательно, как это видно из рис.14, сигнал
действительно является мультифракталом.
Рис. 14. Оценка степени мульти-фрактальности
Для получения временных рядов эволюции
для
временного
ряда
приращений
электротеллурических потенциалов (рис.12(б))
значений мульти-фрактальных параметров для
временного ряда приращений (рис. 12, б) было
выбрано скользящее окно длиной 672 часовых отсчетов, то есть 28 суток, взаимное смещение
соседних окон равнялось 24 отсчетам или 1 суткам. Результаты представлены на рис.15.
Масштабно-зависимые тренды не устранялись, так как рассматривался ряд в приращениях.
( m)
h(q)
Функция h(q) в зависимости Z (q, s) s
оценивалась в каждом окне для масштабов s ,
изменяющихся от минимального значения 30 отсчетов до максимального, равного одной пятой
длины окна. При длине 672 отсчетов, таким образом, максимальный масштаб равен 137 часов. Кроме
того, для этих же временных окон были получены оценки на основе использования статистик (39) для
ряда в приращениях и (40)-(41) и для исходного ряда. При этом, при построении оценки на основе
ортогональных вейвлет-разложений производилось предварительное устранение тренда внутри
каждого окна полиномом 4-го порядка. Эта предварительная операция удаляла статистически
незначимые низкочастотные вариации и, что более важно, уменьшало искажения значений вейвлеткоэффициентов на концах выборки вследствие ее конечности. В каждом окне искался ортогональный
вейвлет из условия минимума энтропии (25) распределения квадратов вейвлет-коэффициентов.
Из рис. 15, а, б видно, что оба метода, (39) и (40)-(41) дают, фактически одно и то же, за
исключением взаимного смещения, которое может быть вызвано несоответствием данных монофрактальному поведению.
Что же касается прочих графиков на рис. 15, то они могут быть использованы при мониторинге
объектов для выделения аномальных признаков. Одним из признаков аномального поведения может
*
служить «провал» вниз значения F ( ) - это может свидетельствовать о появлении во временном
ряду составляющей, поведение которой достаточно сильно отличается от поведения случайной
самоподобной кривой. Кроме того, вариации наиболее типичного показателя Гельдера-Липшица *
и ширины носителя спектра сингулярности могут также нести информацию об изменении
свойств ряда, которые скрыты от их выделения более простыми средствами анализа типа линейной
фильтрации.
Ширина носителя наиболее важна среди параметров мульти-фрактального спектра
сингулярности, так как является мерой разнообразия случайного поведения сигнала. Она, грубо
говоря, отражает число экспонент Гельдера—Липшица. Уменьшение свидетельствует о
подавлении определенных степеней свободы системы, генерирующей изучаемый сигнал,
уменьшении их числа.
0.8
(а)
0.6
0.4
0.2
0.8
(б)
0.4
0
1
F(
0.9
0.8
0.7
0.6
0.6
0.5
0.4
0.3
0.2
0.1
1.2
1
0.8
0.6
0.4
0.2
0
1.2
1
0.8
0.6
0.4
0.2
0.3
max
min
0.2
0.1
0
-0.1
0
200
400
600
800
1000
1200
1400
1600 сутки
Рис. 15. (а) – оценки вариаций постоянных Херста для временного ряда электротеллурических потенциалов в
скользящем временном окне длиной 672 часа RS-методом (формула (39)); (б) – оценка с использованием
ортогональных вейвлет разложений содержимого каждого из окон (формулы (40) и (41)). Прочие графики
представляют изменения параметров спектра сингулярности (обозначения – в тексте)
Например, анализ мульти-фрактальных параметров низкочастотного микросейсмического
шума позволил еще в 2008 г. выдвинуть гипотезу о приближении Японских островов к крупной
сейсмической катастрофе, признаком которой является статистически значимое уменьшение ширины
носителя мульти-фрактального спектра сингулярности. Использование оценок свойств
микросейсмического фона от различных станций позволяет строить пространственные карты их
изменения в скользящих временных окнах. Области минимума значений ширины носителя спектра
сингулярности на последовательности таких карт фактически дает динамическую оценку текущей
сейсмической опасности, причем по устойчивости положения пятна пониженных значений и его
размерам можно оцепить энергию готовящегося сейсмического события [Любушин, 2009, 2011;
Lyubushin, 2012, 2013].
Оценка спектра сингулярности доступно в пакете Spectrf_Analyzer, который может быть скачан
по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/01/SpAn.zip
Руководство пользователя программным пакетом на русском языке доступно по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/01/Spectra_Analyzer.pdf
Оценка параметров спектра сингулярности в скользящем временном окне может быть
произведена программой SingSpect, которая может быть скачана по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/10/SingSpect.zip
с руководством пользователя по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/10/SingSpect.pdf
Оценка наклона вейвлетного спектра мощности (формулы (40-41)) в скользящем временном
окне может быть произведена программой WaveSpectExp, которая может быть скачана по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/09/WaveSpectExp.zip
с руководством пользователя по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/09/WaveSpectExp.pdf
КАНОНИЧЕСКИЕ КОГЕРЕНТНОСТИ И СПЕКТРАЛЬНЫЕ МЕРЫ
СИНХРОННОГО ПОВЕДЕНИЯ
В этом пункте изложены методы анализа большого числа временных рядов с помощью
спектрального подхода. Квадратичный спектр когерентности двух процессов можно определить, как
квадрат коэффициента корреляции этих процессов на частоте . Канонические когерентности
являются обобщением понятия спектра когерентности на ситуацию, когда вместо пары скалярных
временных рядов необходимо исследовать связь на различных частотах между двумя векторными
временными рядами: m -мерным рядом X (t ) и n -мерным рядом Y (t ) . Без ограничения общности
2
будем считать, что n m . Величина 1 ( ) , называемая квадратом модуля первой (максимальной)
канонической когерентности рядов X (t ) и Y (t ) [Brillinger, 1975], которая в данном случае заменяет
обычный спектр когерентности, вычисляется как максимальное собственное число эрмитовой
матрицы
U ( ) S xx1/ 2 S xy S yy1S yx S xx1/ 2 .
(42)
Здесь - частота, S xx ( ) - спектральная матрица размером m m временного ряда X (t ) , S xy ( ) H
кросс-спектральная прямоугольная матрица размером m n , S yx ( ) S xy ( ) , “ H ” – знак эрмитова
2
сопряжения. Величина 1 ( ) заменяет квадрат модуля спектра когерентности в случае двух
многомерных сигналов.
2
Введем понятие покомпонентных канонических когерентностей i ( ) q -мерного временного
ряда Z (t ) [Любушин, 1989, 2007] как квадратов модулей максимальной канонической когерентности
в ситуации, когда в формуле (42) в качестве ряда Y (t ) берется i -ая скалярная компонента q -мерного
ряда Z (t ) , а в качестве X (t ) (q 1) -мерный ряд, состоящий из прочих компонент. Величина
i2 ( ) , таким образом, характеризует связанность на частоте вариаций i -ой компоненты с
вариациями совокупности всех прочих компонент. Введение покомпонентных канонических
когерентностей позволяет определить еще одну частотно-зависимую статистику ( ) ,
характеризующую связанность на частоте вариаций всех компонент векторного ряда Z (t ) :
q
( ) i ( )
i 1
(43)
Заметим, что, в силу построения, значение величины ( ) принадлежат интервалу [0,1] и чем
ближе соответствующее значение к единице, тем сильнее связь между вариациями компонент
многомерного временного ряда Z (t ) на частоте . Следует подчеркнуть, что сравнение абсолютных
значений статистики ( ) возможно лишь для одного и того же числа q одновременно
обрабатываемых временных рядов – поскольку, в силу формулы (42), при росте q величина ( )
убывает, как произведение q величин, меньших единицы. Если q 2 , то мера (43) становится
обычным квадратом модуля спектра когерентности.
Чтобы оценить изменчивость во времени взаимодействия регистрируемых процессов,
необходимо производить вычисления в скользящем временном окне заданной длины. Пусть временная координата окна длиной L отсчетов. Вычисляя спектральные матрицы для выборок,
попавших во временное окно , получим двухпараметрическую функцию ( , ) . Всплески
величины ( , ) будут определять частотные полосы и временные интервалы увеличения
коллективного поведения совместно анализируемых процессов.
Для реализации этого алгоритма необходимо иметь в каждом временном окне оценку
спектральной матрицы S zz ( , ) размером q q . Далее предпочтение отдается использованию
модели векторной авторегрессии [Marple, 1987]. Метод заключается в оценке параметров модели:
p
Z (t ) A k Z (t k ) e(t ) .
(44)
k 1
Здесь A k - матрицы авторегрессионных параметров размером q q , p - порядок авторегрессии, e(t )
- q -мерный временной ряд остатков идентификации, относительно которого предполагается, что он
является последовательностью независимых случайных векторов с нулевым средним и неизвестной
T
ковариационной матрицей M {e(t )e (t )} , которая считается независящей от времени.
Важно отметить, что перед вычислением спектральной матрицы в каждом временном окне
независимо производится следующая последовательность предваряющих операций для каждой
скалярной компоненты многомерного временного ряда. Прежде всего, устранялся общий линейный
тренд и производился переход к приращениям. Далее осуществлялась винзоризация [Huber, 1981]:
итеративно вычислялись выборочные значения среднего и стандартного отклонения , из выборки
среднее значение вычиталось, после чего отсчеты делились на и все значения, выходящие за
пороги 3 , заменялись на эти пороговые значения. Итерации повторялись до тех пор, пока не
переставала меняться. Эти операции обеспечивают устойчивость оценки меры когерентности по
отношению к выбросам.
Для оценки матриц A k и используется рекуррентная процедура Дарбина-Левинсона
[Marple, 1987], для которой необходимо предварительно вычислить выборочные оценки
T
ковариационных матриц R k M {Z (t )Z (t k )}, k 0,1,..., p .
Оценка спектральной матрицы вычисляется по формуле:
p
S zz ( ) F 1 ( ) F H ( ), F ( ) E A k exp(ik )
(45)
k 1
E - единичная матрица размером q q . Оценка (45) обладает хорошей разрешающей
способностью по частоте для коротких выборок. Для выбора порядка авторегрессии p не
существует надежных формализованных процедур. В расчетах выбор p производился методом проб,
как такое минимальное значение, для которого дальнейшее увеличение не приводит к существенному
изменению основных элементов поведения зависимости ( , ) .
В качестве примера применения спектральной меры когерентности рассмотрим задачу о
синхронизации мульти-фрактальных параметров глобального сейсмического шума [Любушин, 2014
а, b; Lyubushin, 2015].Использовалась информация от широкополосных сейсмических станций из
объединения 3-х глобальных сейсмических сетей:
Global Seismographic Network: http://www.iris.edu/mda/_GSN
GEOSCOPE: http://www.iris.edu/mda/G
GEOFON: http://www.iris.edu/mda/GE
Скачивались данные вертикальных компонент с частотой дискретизации 1 Гц за 18 лет
наблюдений, с 01 января 1997 г. по 31 декабря 2014 г. Далее сейсмические записи приводились к
шагу по времени 1 мин путем вычисления средних значений в последовательных временных
интервалах длиной 60 значений.
На рис. 16 представлены положения 229 широкополосных станций, информация от которых
использовалась для анализа свойств сейсмического шума. Совокупность всех станций разбита на 8
групп, которые также представлены на рис. 16 с указанием числа станций в каждой группе. Имена
групп станций состоят из 3-х букв, которые имеют следующую мнемонику: “N” – север, “S” – юг,
“W” – запад, “E” – восток. Например, группа станций NES означает станции из Северного полушария
(первая буква “N”), имеющие восточные долготы (вторая буква “E”) и их южная часть (третья буква
“S”). Принцип разбиения станций на группы был следующий: сначала станции были разбиты по
принципу их географического положения на Северное и Южное полушария, которые потом делились
на западную и восточную части (по знаку долготы). Таким образом, были получены 4 группы NW,
NE, SW, SE. Далее каждая из полученных 4-х групп была разбита на 2 части, северную и южную,
граница по широте между которыми выбиралась из условия примерного равенства числа станций в
каждой подгруппе.
90
NEN(49)
NWN(34)
60
30
NES(50)
NWS(35)
0
SWN(13)
SEN(17)
-30
SWS(13)
SES(18)
-60
-90
-180
-120
-60
0
60
120
180
Рис. 16. Положения 229 широкополосных станций объединения 3-х глобальных сейсмических сетей и их
разбиение на 8 групп. В скобках после имени группы указано число станций в группе
Ниже при анализе низкочастотных микросейсм использовались оценки спектра сингулярности
в последовательных непересекающихся временных окнах длиной 1 сут (1440 отсчетов). Локальные
тренды удалялись полиномами 8-го порядка.
На рис. 17 представлены графики ежесуточных медиан статистик lg(Var ) , , En и для
каждой из 8 групп станций на рис. 16 вместе с графиками их скользящих средних во временном окне
длиной 57 суток. На графиках усредненных значений заметны сезонные вариации для некоторых
групп станций, особенно для групп станций NEN и NWN. Далее нас будут интересовать эффекты
когерентного поведения компонент двух 8-мерных временных рядов, представленных на рис. 17.
На рис. 18 представлены частотно-временные диаграммы спектральной меры когерентности
(43) для вариаций исследуемых параметров сейсмического шума (рис.18). Оценки вычислены в
скользящем временном окне диной 365 суток (1 год) со смещением 7 суток. Использовалась
векторная авторегрессионная модель 5-го порядка. В каждом окне производился предварительный
переход к приращениям.
Видно, что частотно-временные карты ( , ) характеризуются всплесками когерентности с
нарастающей амплитудой, причем максимумы всплесков когерентности приходятся на диапазон
периодов от 5 до 10 суток.
*
1.6
NWN
NEN
0.6
NEN
NWN
1.2
0.4
0.8
0.4
0.2
0
2000
2004
2008
2012
2000
2008
2012
2000
NES
0.6
NWS
2004
2004
2008
2012
NWS
1.6
2000
2008
2012
2008
2012
2008
2012
2008
2012
NES
1.2
0.4
2004
0.8
0.4
0.2
0
2000
2004
2008
2000
2012
0.6
SWN
2004
2008
2012
2000
SEN
2004
2008
2012
SWN
1.6
2000
SEN
1.2
0.4
2004
0.8
0.4
0.2
0
2000
2004
2008
2012
2000
0.6
SWS
2004
2008
2012
2000
SES
2004
2008
2012
1.6
2000
SES
1.2
SWS
0.4
2004
0.8
0.4
0.2
0
2000
2004
2008
2012
2000
2004
2008
2012
2000
2004
2008
2012
2000
2004
Рис. 17. Графики ежесуточных медиан мульти-фрактальных свойств сейсмического фона, вычисленных для 8
групп станций (рис. 16). Толстые зеленые линии – средние значения в скользящем временном окне длиной 57
суток
Рис. 18. Частотно-временные диаграммы меры когерентности временных рядов, представленных на рис. 17
Постепенное увеличение синхронизации параметров глобального сейсмического шума в
работах [Любушин, 2014 а, b; Lyubushin, 2015] интерпретируется как индикатор увеличения
глобальной сейсмической опасности и сопровождается усилением интенсивности сильнейших
землетрясений во всем мире, которое началось с землетрясения 26 декабря 2004 года на Суматре.
Оценка эволюции спектральной меры когерентности поведения многомерного временного ряда
в скользящем временном окне может быть произведена с помощью программы SpectCohMes, которая
может быть скачана по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/05/SpectCohMes.zip
с руководством пользователя по адресу:
http://old.ifz.ru/scient_directions/data_monitoring/05/SpectCohMes.pdf
Данные, которые использовались в примерах, можно скачать внутри zip-файла по адресу:
https://yadi.sk/d/7GRY2LOgiJQgz. В именах файлов данных явно указано, в каких рисунках они были
использованы, например, Data_Ris_01.dat или Data_Ris_12,13,14,15.dat. Многомерные данные для
рисунков 17 и 18 содержатся внутри директории [Data_Ris_17,18].
ЛИТЕРАТУРА
Любушин А.А. (2007) Анализ данных систем геофизического и экологического мониторинга. М.:
Наука. 2007. 228 с.
Любушин А.А. Анализ канонических когерентностей в задачах геофизического мониторинга // Физика
Земли. 1998. № 1. С. 59-66.
Любушин А.А. Анализ когерентности глобального сейсмического шума, 1997-2012 // Физика Земли.
2014а. №3. С. 18-27.
Любушин А.А. Прогностические свойства случайных флуктуаций геофизических характеристик //
Биосфера. 2014b. №4. С. 319-338.
Любушин А.А. Разведочный анализ свойств временных рядов на основе использования интерактивной
программы Spectra_Analyzer: Учебное пособие для старших курсов геофизического факультета.
М.: РГГРУ. 2006. 46 с. http://window.edu.ru/resource/967/71967
Любушин А.А. Сейсмическая катастрофа в Японии 11 марта 2011 года. Долгосрочный прогноз по
низкочастотным микросейсмам. // Геофизические процессы и биосфера. 2011. T. 10, № 1. C.9-35.
Любушин А.А. Тренды и ритмы синхронизации мультифрактальных параметров поля низкочастотных
микросейсм. // Физика Земли. 2009. № 5. C. 15-28.
Любушин А.А., Копылова Г.Н. Многомерный вейвлет-анализ временных рядов электротеллурических
наблюдений на Камчатке // Физика Земли. 2004. №2. C.82-96.
Р. 87-114.
Box G.E.P., G.M.Jenkins. Time series analysis. Forecasting and control. Holden-Day. San Francisco,
Cambridge, London, Amsterdam: 1970 (Русский перевод: Бокс Дж., Дженкинс Г. Анализ временных
рядов. Прогноз и управление. М.: Мир, 1974. B 2-х выпусках. 406с. и 197с.).
Brillinger D.R. Time series. Data analysis and theory. Holt, Rinehart and Winston, Inc. N.Y., Chicago, San
Francisco: 1975 (Русский перевод: Бриллинджер Д. Временные ряды. Обработка данных и теория.
М.: Мир. 1980. 536с.)
Chui, C.KAn Introduction to Wavelets, Academic Press, San Diego, CA: 1992. (Русский перевод: Чуи Ч.
Введение в вэйвлеты. М.: Мир. 2001. 412 с.).
Dansgaard, W., Johnsen, S. J., Reeh, N., Gundestrup, N., Clausen, H. B., Hammer, C. U. Climatic changes,
Norsemen and modern man // 1975. Nature. V. 255: P. 24-28.
Daubechies I. Ten Lectures on Wavelets. № 61 in CBMS-NSF Series in APlied Mathematics, SIAM,
Philadelphia: 1992. (Русский перевод: Добеши И. Десять лекций по вейвлетам. Ижевск: НИЦ
"Регулярная и хаотическая динамика". 2001. 464 с.).
Donoho D., I. Johnstone Ideal spatial adaptation via wavelet shrinkage. 1994. Biometrika. V. 81. P. 425455.
Feder J. Fractals. Plenum Press, New York, London: 1988 (Русский перевод: Федер Е. Фракталы. М.:
Мир. 1991. 254с.)
Hardle W. Applied nonparametric regression. Cambridge University Press, Cambridge, New York, New
Rochell, Melbourne, Sydney: 1989 (Русский перевод: Хардле В. Прикладная непараметрическая
регрессия. М.: Мир. 1993. 349 с.)
http://alexeylyubushin.narod.ru/Geophysical_Monitoring_Systems_Data_Analysis_Book_Rus.pdf
Huber P.J. Robust statistics. John Wiley and Sons. New York, Chichester, Brisbane, Toronto: 1981.
(Русский перевод: Хьюбер П. Робастность в статистике. М.: Мир. 1984. 303 с.).
Hurst H.E. Long-term storage capacity of reservoirs // Trans. Amer. Soc. Civ. Eng. 1951. V. 116. P.770808.
Kanasewich E.R. Time Series Analysis in Geophysics. The University of Alberta Press. Edmonton: 1981.
(Русский перевод: Канасевич Э.Р., Анализ временных последовательностей в геофизике. М.:
Недра. 1981. 400с.).
Kantelhardt J. W., Zschiegner S. A., Konscienly-Bunde E., Havlin S., Bunde A., and Stanley H. E.
Multifractal detrended fluctuation analysis of nonstationary time series // Physica A. 2002. № 316.
Kashyap R.L., A.R.Rao. Dynamic stochastic models from empirical data. Academic Press. N.Y., San
Francisco, London: 1976. (Русский перевод: Кашьяп Р.Л., А.Р.Рао. Построение динамических
стохастических моделей по экспериментальным данным. М.: Наука. 1983. 384с.).
Lyubushin A.A. Wavelet-based coherence measures of global seismic noise properties // Journal of
Seismology. April 2015. V. 19, Issue 2. P 329-340.
Lyubushin A.A., Klyashtorin L.B. Short term global dT prediction using (60-70)-years periodicity // Energy
& Environment, 2012, V. 23, No.1, pp.75-85. doi: 10.1260/0958-305X.23.1.75.
Lyubushin, A. How soon would the next mega-earthquake occur in Japan? // Natural Science.2013. V.5,
№ 8A1. P. 1-7. http://www.scirp.org/journal/PaperInformation.aspx?PaperID=35770
Lyubushin, A. Prognostic properties of low-frequency seismic noise // Natural Science. 2012. № 4. P. 659666. http://www.scirp.org/journal/PaperInformation.aspx?paperID=21656
Mallat S. A wavelet tour of signal processing. Academic Press. San Diego, London, Boston, N.Y., Sydney,
Tokyo, Toronto: 1998. 577 p. (Русский перевод: Малла С. Вэйвлеты в обработке сигналов. М.: Мир.
2005. 671 c.).
Mandelbrot B.B., Wallis J.R. Some long-term properties of geophysical records // Water Resources Res.
1969. V. 5. P. 321-340.
Marple S.L.(Jr.) Digital spectral analysis with applications. Prentice-Hall, Inc. Englewood Cliffs, New
Jersey: 1987. (Русский перевод: Марпл С.Л. Цифровой спектральный анализ и его приложения. М.:
Мир. 1990. 584с.).
Press W.H., Flannery B.P., Teukolsky S.A. and Vettering W.T. Numerical Recipes, 2-nd edition, Chapter
14.8, Savitzky-Golay Smoothing Filters. Cambridge Univ. Press, Cambridge: 1996a.
Press W.H., Flannery B.P., Teukolsky S.A. and Vettering W.T. Numerical Recipes, 2-nd edition, Chapter
13.10, Wavelet Transforms, Cambridge Univ. Press, Cambridge: 1996b.