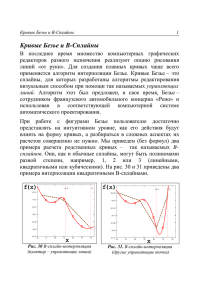
Нейросетевая аппроксимация векторных объектов кривыми безье
advertisement

ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1 А.А. ШИРМА Воронежский государственный педагогический университет escriptum@mail.ru НЕЙРОСЕТЕВАЯ АППРОКСИМАЦИЯ ВЕКТОРНЫХ ОБЪЕКТОВ КРИВЫМИ БЕЗЬЕ Рассматривается задача определения коэффициентов аппроксимирующих полиномов по точкам контура растрового площадного объекта. Предложен и реализован алгоритм декомпозиции сложных кривых и вычисления на основе гистограммного кодирования коэффициентов контуров соответствующих им кривых Безье. Такими информационными признаками могут выступать статистические характеристики. Ключевые слова: нейронная сеть, кривая Безье Введение При решении задачи векторизации растровых изображений возникает необходимость представления кривых с помощью математических выражений. Такое представление значительно компактнее дискретных представлений, но его поиск связан с определёнными трудностями в связи с тем, что точные значения обрабатываемых кривых нередко бывают искаженными из-за наличия шума, погрешностей дискретизации или отклонений при сегментации. Компромиссным решением данной проблемы является проведение кривой вблизи множества точек, принадлежащих исходным данным, то есть их аппроксимация. В качестве математического описания кривых распространены методы, предусматривающие использование линейных, кусочно-линейных, полиномиальных и кусочно-полиномиальных функций различных типов, но именно последние получили наибольшее распространение [1]. В подобных методах аппроксимации кривые рассматриваются как множество дуг кривых и элементарных кусков поверхности, соединенных между собой, каждый из которых может быть задан своим аналитическим выражением. Таким выражением, в силу своей простоты и точности описания произвольного контура, может быть взята кривая Безье [2]. К примеру, кубические полиномы, соответствующие таким кривым, позволяют описать функцию, имеющую непрерывную вторую производную в точках УДК 004.032.26(06) Нейронные сети 32 ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1 сопряжения двух соседних кривых, что является необходимым условием для объединения в более сложные сплайны. Проблема построения наиболее точной аппроксимации заключается в поиске оптимальных коэффициентов кривых Безье. Если прямая задача получения кривой по заданным коэффициентам полиномов является тривиальной, то обратная задача − определение коэффициентов аппроксимирующих полиномов по точкам кривой − не имеет простого решения и часто носит итерационный характер, количество итераций которого в сложных случаях доходит до 300 [1, 3]. Для решения этой проблемы в работе предлагается применять гистограммное кодирование контуров, заданных кривыми Безье, и использование информативных признаков в качестве входа нейронной сети. Проблема гистограммного кодирования была рассмотрена Куссулем [4], но с упором не на точную передачу контуров, а на их классификацию. Постановка задачи и описание алгоритма В параметрической форме кубическая кривая Безье описывается следующими уравнениями: x(t ) (1 t )3 x0 3t (1 t ) 2 x1 3t 2 (1 t ) x2 t 3 x3 , (1) (2) у(t ) (1 t )3 у0 3t (1 t )2 у1 3t 2 (1 t ) у2 t 3 у3 , где t [0,1]; ( x0 , y0 ) и ( x3 , y3 ) – её начало и конец; ( x1 , y1 ) и ( x2 , y2 ) – управляющие точки; ( x0 , y0 ) ( x1 , y1 ) – касательная в точке ( x0 , y0 ) и ( x2 , y2 ) ( x3 , y3 ) – касательная в точке ( x3 , y3 ). Таким образом, каждый график может быть представлен вектором w ( x0 , y0 , x1 , y1 , x2 , y2 , x3 , y3 ), компонентами которого являются коэффициенты уравнений кривой Безье. Описание графика в виде вектора w, всегда имеет одно и то же количество компонентов независимо от числа точек в кривой, что упрощает решение различных задач, в частности, задачи аппроксимации. То есть задачу описания графиков в дискретном пространстве можно перенести в пространство коэффициентов, аппроксимирующих их полиномов. Аппроксимацию кривой Безье можно рассматривать как пошаговое уточнение формы многоугольника, получаемого последовательным соединением ее контрольных точек. При этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника, а форма опреУДК 004.032.26(06) Нейронные сети 33 ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1 деляется относительным расположением оставшихся точек, через которые в общем случае она не проходит. В данной работе ставилась задача разработки метода, позволяющего использовать описания контуров кривыми Безье для поиска такого набора коэффициентов w, при которых расстояние между аппроксимирующей и экспериментальной кривыми было бы минимально. Ошибку, которая связана с каждой точкой ( xi , yi ), можно измерить расстоянием от этой точки до аппроксимирующей кривой по нормали к ней и записать следующей формулой: M yi g ( xi ) . (3) i 1 Таким образом, для вычисления расстояния от каждой точки графика до аппроксимирующей кривой должна быть найдена соответствующая ближайшая точка на аппроксимирующей кривой, что само по себе при параметрическом задании кривой является итерационной задачей. При значительном количестве точек на графике и заранее не определенном количестве итераций такой способ решения задачи приводит к существенным вычислительным трудностям. Интересную меру сходства предлагают использовать в работе [3]. В качестве меры сходства экспериментального графика с некоторой аппроксимирующей кривой предлагается принять площадь S(w, y(x)) фигуры, ограниченной контуром, образованным упомянутой кривой, определяемой коэффициентами w, и экспериментальной кривой, образованной точками кривой, отображающей некоторую неизвестную функцию y(x). Тогда поиск кривой Безье с коэффициентами wopt, которая наилучшим образом аппроксимирует заданную экспериментальную кривую, можно рассматривать как определение её коэффициентов, которые минимизируют значение S(w, y(x)): (4) wopt arg min S (w, y( x)). Нейронная сеть является универсальным аппроксиматором и при правильном выборе её структуры может достаточно точно аппроксимировать любую непрерывную функцию. Для моделирования была выбрана статическая двухслойная сеть с прямой передачей сигнала, состоящая из одного слоя нейронов с сигмоидной функцией активации и второго слоя с линейной функцией активации. Сети с такой архитектурой могут воспроизводить весьма сложные нелинейные зависимости между входом и выходом сети [5]. УДК 004.032.26(06) Нейронные сети 34 ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1 Нейронные сети имеют фиксированное число входов. Причем каждый вход нейронной сети рассматривается как отдельный признак объекта (в идеале – независимый признак). Поэтому для использования в качестве входов нейронной сети коды объектов должны удовлетворять следующим двум условиям: 1) любой код объекта имеет всегда одну и ту же длину; 2) каждый вход сети (элемент кода объекта) всегда отражает одну и ту же характеристику этого объекта. Кодирование контуров Если граница объекта содержит одну или несколько хорошо выраженных вогнутостей, несущих информацию о форме объекта, то она подвергается декомпозиции. В этом случае мощным инструментом для устойчивой декомпозиции границы является использование выпуклой оболочки области, находящейся внутри границы [6]. Выпуклая оболочка H произвольного множества S есть наименьшее выпуклое множество, содержащее S. Разность множеств H\S называется дефектом выпуклости D множества S. Рис. 1. Декомпозиция контура на сегменты Разбиение границы области осуществляется путём обхода контура𝑆и пометки точек входа в область дефекта выпуклости и выхода из неё. На рис. 1 круглыми маркерами показано местоположение таких точек, а звёздами – выпуклая оболочка. Эти точки могут быть найдены, исходя из скорости изменения угла, то есть кривизны наклона. Например, точка p может считаться частью почти прямолинейного отрезка границы, если изменение крутизны не превышает 100, или же угловой, если это изменение более 900. Однако в общем УДК 004.032.26(06) Нейронные сети 35 ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1 случае трудно надёжно измерить кривизну в некоторой точке дискретной границы, потому что обычно на таких границах имеются локальные «зазубрины» и её интерпретация зависит от длины отдельных сегментов по отношению к общей длине границы [6]. Поэтому для каждой пары точек выпуклой оболочки ищутся наиболее дефектные области выпуклости. К примеру, если расстояние от линии выпуклой оболочки до максимального значения на текущем участке кривой превышает три пиксела, то концевые точки помечаются как сегментные. Теперь выделенные сегменты границы можно количественно описать с помощью простых статистических характеристик, таких как среднее, дисперсия и моменты более высокого порядка. (а) (б) Рис 2. Участок границы (а) и его представление одномерной функцией (б) На рис. 2,б участок границы представлен в виде одномерной функции g(r) свободной переменной r. Эта функция получается путем соединения отрезком двух крайних точек границы (см. рис. 2,а) и последующим поворотом его до горизонтального положения. Координаты точек границы поворачиваются на тот же угол. УДК 004.032.26(06) Нейронные сети 36 ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1 Будем рассматривать амплитуду функции g как дискретную случайную величину v и построим её гистограмму p(vi ) , i = 0,1,2,…, A-1, где A – число дискретных интервалов, на которые разбит диапазон амплитуд. Учитывая затем, что p(vi ) является оценкой вероятности появления значения vi , можно записать следующие выражения для центрального момента порядка n случайной величины v: A1 n (v) (vi m) n p(vi ) , (5) i 0 где m A 1 vi p(vi ) . i 0 (6) Величина m есть математическое ожидание, а 2 – дисперсия случайной величины v. В общем случае требуется лишь несколько первых моментов, чтобы различить сигнатуры границ явно отличающихся форм. Преимущество моментов перед другими методами заключается в простоте реализации, а также в том, что они позволяют «физически» интерпретировать форму границы. Данный метод инвариантен к повороту объекта, а нормировку по размерам можно при желании получить путём масштабирования диапазона значений g и r. Таким образом, исходя из задачи, вектор входа выглядит следующим образом: (7) X k mk , 2k , 3k . Тогда для точного описания замкнутого контура потребуется 3k параметров, где k – количество кривых Безье. Заключение Предложен и реализован алгоритм декомпозиции сложных кривых и вычисления на основе гистограммного кодирования коэффициентов контуров соответствующих им кривых Безье. Список литературы 1. Павлидис Т. Алгоритмы машинной графики и обработки изображений. М.: Радио и Связь. 1986. 394 с. УДК 004.032.26(06) Нейронные сети 37 ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1 Роджерс Д., Адамс Дж. Математические основы машинной графики: Пер. с англ. – Мир, 2001. 604 с. Вишневский В.В., Рысцов І.К., Волжева М.В. Итерационный алгоритм построения кривой Безье по заданным точкам // Математические машины и системы. 2004. № 4. С. 108–116. Куссуль М.Э. Кодирование контуров, представленных кривыми Безье, в задачах нейросетевой классификации / Куссуль М.Э. // Математические машины и системы. 2004. № 3. Потемкин В.Г. Нейронные сети. Matlab 6. М.: Диалог-МИФИ. 2002. 496 с. Гонсалес, Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс. М.: Техносфера. 2006. 1072 с. УДК 004.032.26(06) Нейронные сети 38