Тема 7. Корреляционно-регрессионный анализ
advertisement
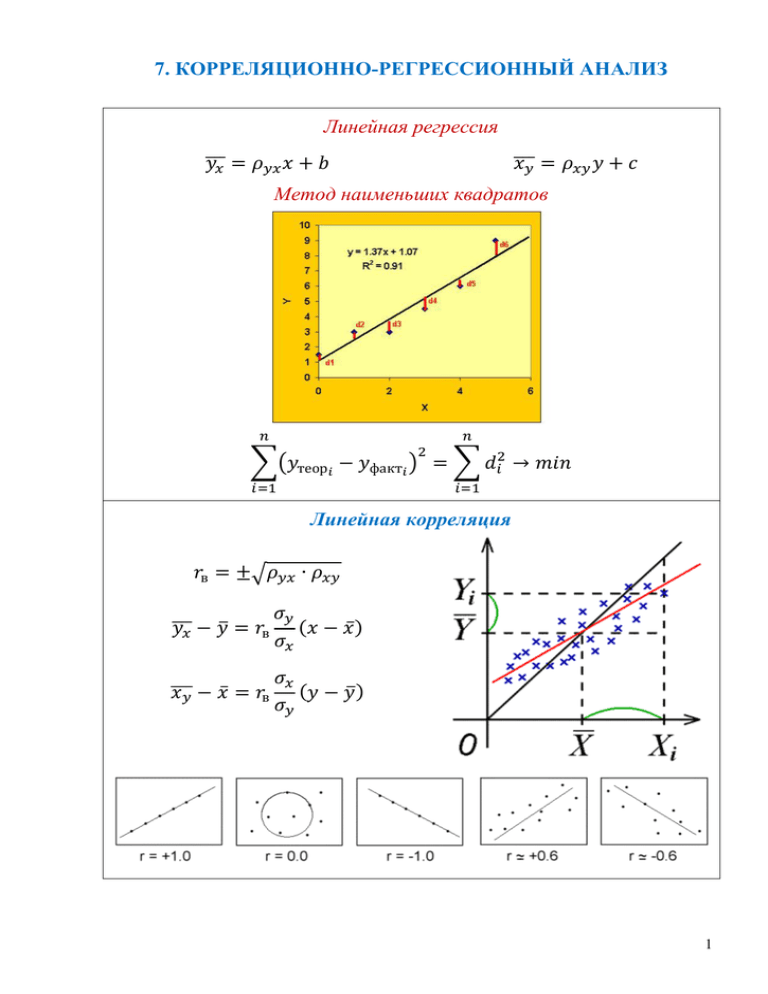
7. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Линейная регрессия ̅̅̅ ̅̅̅ Метод наименьших квадратов ∑( ) ∑ Линейная корреляция √ ̅̅̅ ̅ ( ̅) ̅̅̅ ̅ ( ̅) 1 Практическое занятие №7 КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Для решения практических задач часто требуется установить и оценить зависимость одной случайной величины от других случайных величин. Зависимость величины Y от Х называется функциональной, если каждому значению величины Х соответствует единственное значение величины Y (например, ). Но на практике функциональная зависимость реализуется редко, так как случайные величины подвержены также действию случайных факторов. Если среди этих случайных факторов есть такие, которые воздействуют и на Х, и на Y, то возникает статистическая (стохастическая) зависимость. Зависимость величины Y от Х называется статистической, если каждому фиксированному значению величины Х соответствует не одно, а множество значений переменной Y со своими вероятностями. Если при изменении одной случайной величины изменяется среднее значение другой случайной величины, то такая статистическая зависимость называется корреляционной. Пример 1. Примерами корреляционной связи являются зависимости: между пределами прочности и текучести стали определенной марки; между погрешностью размера и погрешностью формы поверхности детали, обработанной определенным методом; между усилием прижима ролика и шероховатостью накатанной поверхности. Введем понятие условных средних. Условным средним ̅ называют среднее арифметическое наблюдавшихся значений случайной величины Y, соответствующих значению x случайной величины Х. Условным средним ̅̅̅ называют среднее арифметическое наблюдавшихся значений случайной величины X, соответствующих значению y случайной величины Y. Пример 2. При значении случайной величины Х х=3 случайная величина Y принимала значения 4, 6, 14. Определить условное среднее ̅̅̅ . ̅̅̅̅ ̅̅̅ ( ) . Уравнение вида ̅ ( ) называется выборочным уравнением регрессии Y на Х. Уравнение вида ̅̅̅ ( ) называется выборочным уравнением регрессии Х на Y. Ограничимся рассмотрением наиболее распространенного случая, когда функции ( ) и ( ) линейны. Статистические связи между переменными можно изучать методами корреляционного и регрессионного анализа. Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. Основной задачей корреляционного анализа является выявление связи между случайными переменными и оценка ее силы (тесноты). Линейная регрессия При линейной корреляционной зависимости классические уравнения регрессии можно записать в виде: ̅ , ̅̅̅ , где , - выборочные коэффициенты регрессии Y по Х и Х по Y соответственно. Для определения неизвестных параметров уравнений применяют метод наименьших квадратов (МНК). Согласно методу числовые значения параметров уравнений определяются таким образом, чтобы сумма квадратов отклонений 2 условных средних теоретических (найденных по уравнению регрессии) и фактических (эмпирических), была минимальной: ∑( ) ∑( ̅) Итоговые расчетные формулы для определения параметров линейной регрессии МНК приведены в табл. 1. Таблица 1 ̅ ∑ ∑ ∑ ∑ (∑ ) ∑ ∑ ∑ ∑ ∑ (∑ ) ̅̅̅ ∑ ∑ ∑ ∑ (∑ ) ∑ ∑ ∑ ∑ ∑ (∑ ) Пример 3. В результате исследований зависимости двух случайных величин Х и Y были получены следующие экспериментальные данные: 1,00 1,50 3,00 4,50 5,00 1,25 1,40 1,50 1,75 2,25 Определить параметры выборочного уравнения линейной регрессии Y на Х и Х на Y. 1. Составим вспомогательную таблицу (n = 5): i 1 2 3 4 5 Σ 1,00 1,50 3,00 4,50 5,00 15,00 1,25 1,40 1,50 1,75 2,25 8,15 1,25 2,10 4,50 7,88 11,25 26,98 1,00 2,25 9,00 20,25 25,00 57,50 1,56 1,96 2,25 3,06 5,06 13,89 2. Определим параметры линейной регрессии: ̅̅̅ ̅̅̅ Линейная корреляция Из уравнений регрессии следует, что коэффициенты регрессии и ⁄ определяют угловые коэффициенты (тангенсы углов наклона) к оси Х соответствующих линий регрессии. Следовательно, коэффициенты регрессии можно использовать для оценки силы (тесноты) корреляционной зависимости. Однако коэффициенты регрессии имеют размерность и зависят от единиц измерения. Поэтому на практике для оценки тесноты линейной корреляционной зависимости переменных Х и Y используют выборочный коэффициент корреляции как средней геометрической коэффициентов регрессии, имеющей их знак: . √ С учетом коэффициента корреляции выборочные уравнения линейной ре( ( грессии приводят к следующему виду: ̅ ̅ ̅ ), ̅̅̅ ̅ ̅ ). При этом дает количественную оценку тесноты связи между переменными Х и Y. Отметим основные свойства коэффициента корреляции: ], при этом, чем т.е. принимает значения на отрезке [ ближе | | к единице, тем теснее связь между переменными Х и Y; 3 при корреляционная связь представляет линейную функциональную зависимость; при линейная корреляционная связь между Х и Y отсутствует (но это не означает невозможность наличия между ними нелинейной связи); указывает на наличие обратной зависимости между переменными Х и Y: при увеличении одной переменной другая уменьшается; указывает на наличие прямой зависимости между переменными Х и Y: при увеличении (уменьшении) одной переменной другая тоже увеличивается (уменьшается); если все значения переменных умножить на одно и то же число, то величина коэффициента корреляции не изменится. В практических исследованиях о тесноте корреляционной зависимости между рассматриваемыми переменными судят фактически не по величине генерального коэффициента корреляции (который обычно неизвестен), а по величине выборочного коэффициента корреляции. Коэффициент определяется по выборке и является случайной величиной. Поэтому возникает вопрос: действительно ли полученное значение объясняется наличием существующей линейной корреляционной зависимости между переменными Х и Y, или является следствием случайности отбора переменных в выборку. Для ответа на него необходимо проверить гипотезу о значимости выборочного коэффициента корреляции. Проверка гипотезы о наличии линейной корреляционной связи Пусть двумерная генеральная совокупность (Х, Y) распределена нормально. Из этой совокупности извлечена выборка объема n и по ней найден выборочный коэффициент корреляции . Далее проверяется нулевая гипотеза о равенстве нулю генерального коэффициента корреляции (т.е. ). Если нулевая гипотеза принимается, то это означает, что линейная корреляционная связь между Х и Y отсутствует; в противном случае – Х и Y коррелированны. В основу проверки данной гипотезы положен критерий: √ √ , который при выполнении нулевой гипотезы имеет распределе- ние Стьюдента (t – распределение) с числом степеней свободы . Поскольку в качестве альтернативной гипотезы принимают , границы двусторонней критической области ( ) определяют по соответствующей таблице (Приложение 6). Далее проверяется принадлежность критической области W. Подробное содержание и особенности этапов проверки приведены в табл. 2. Пример 4. На базе экспериментальных данных примера 3 и найденных коэффициентов регрессии определить выборочный коэффициент корреляции и проверить гипотезу о наличии линейной корреляционной связи между переменными Х и Y. Выборочный коэффициент корреляции . √ √ 1. Принимаем . 2. Назначаем . 3. Согласно проверяемой гипотезе в основе проверки лежит критерий: √ √ свободы , имеющий распределение Стьюдента ( - распределение) с числом степеней . 4 4. Согласно гипотезе критическая область W – двусторонняя: по Приложению 6 находим двустороннюю критическую точку ( ) ( ) ; . √ 5. . Т.к. √ нулевая гипотеза противоречит опытным данным. Можно сделать вывод, что выборочный коэффициент корреляции значим (значимо отличается от нуля) и между переменными Х и Y наблюдается линейная корреляционная зависимость. Таблица 2 1. Выбор гипотез 2. Назначение и 3. Критерий √ √ – распределение, , Приложение 6 4. Критическая область 5. Критерий отклонения Двусторонняя: ( ) ; или Проверка гипотезы о законе распределения Одной из важнейших задач математической статистики является установление теоретического закона распределения случайной величины на основании экспериментальных данных. Вид закона распределения определяется из опыта аналогичных предшествующих исследований, теоретических предпосылок и, наконец, на основании графического изображения эмпирического распределения. Параметры закона распределения обычно неизвестны и их заменяют на соответствующие выборочные оценки. Как бы хорошо ни был подобран теоретический закон распределения, между эмпирическим и теоретическим распределениями неизбежны расхождения. Поэтому возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами (связанными с ограниченным числом наблюдений) или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно. Для ответа на этот вопрос и служат критерии согласия. В наиболее часто применяемом критерии -Пирсона в качестве меры расхождения берется величина, равная сумме квадратов отклонений эмпирических и теоретических частот: ∑ ( ) Доказано, что при статистика имеет -распределение с степенями свободы, где - число интервалов вариационного ряда, - число параметров теоретического распределения, вычисленных по экспериментальным данным. ), малочисленные частоПоскольку необходимо выполнение условия ( ты ( ) следует объединить, в этом случае и соответствующие им теоретические частоты также складываются. Если производилось объединение частот, то при определении числа степеней свободы следует в качестве принять число групп выборки, оставшихся после объединения частот. Согласно критерию критическая область – правосторонняя, ее границу определяют по Приложению 5. Cодержание и особенности этапов проверки статистической гипотезы о нормальном законе распределения приведены в табл. 3. 5 Для нормального закона распределения теоретические частоты вычисляют по формуле: ( ), где – объем выборки; - шаг (разность между двумя соседними значениями); ̅̅̅, - выборочные оценки неизвестных парамет̅̅̅ ров распределения; ; ( ) определяют по таблице Приложения 1. Таблица 3 1. Выбор гипотез 2. Назначение (̅ 3. Критерий ∑ ( ) – распределение ) Приложение 5 4. Критическая область 5. Критерий отклонения ( Правосторонняя: ) Пример 5. В таблице представлены изменения выработки на одного основного рабочего. Проверить гипотезу, что выработка рабочих цеха распределена по нормальному закону. Выработка, % 94-100 100-106 106-112 112-118 118-124 124-130 130-136 136-142 3 7 11 20 28 19 10 2 , чел. Первоначально определяем характеристики: ̅̅̅ ; . В предположении, что выработка рабочих цеха распределена нормально, вычисляем теоретические частоты: ) ; ( ; ( )= 1,5 и т.д. В результате имеем: 1,5 5,9 14,1 22,8 24,7 18,2 , чел. После объединения малочисленных частот число интервалов сокращается: 10 11 20 28 19 7,4 1. Принимаем 3. Согласно гипотезе 14,1 ( 22,8 24,7 8,7 12 18,2 ) 2. Назначаем в основе проверки лежит критерий: 2,9 11,6 . ∑ ( ) и ю- щий и Пи с числом степеней свободы . 4. Согласно критерию критическая область W – правосторонняя: ( ) ( ) (по Приложению 5). 5. Т.к. нулевая гипотеза принимается, т.е. предположение о выбранном теоретическом нормальном законе согласуется с опытными данными. Задачи для самостоятельной работы Задача 1. В результате исследований зависимости двух случайных величин Х и Y были получены следующие экспериментальные данные: 2 3 4 5 6 1,9 1,7 1,8 1,6 1,4 1. Предполагая линейную корреляцию определить параметры выборочного уравнения линейной регрессии Y на Х и Х на Y. 2. Определить выборочный коэффициент корреляции и проверить гипотезу о наличии линейной корреляционной связи между переменными Х и Y. 6 Задача 2. Экспериментальные значения случайной величины Х составили: 5 7 9 11 13 15 17 19 15 26 25 30 26 21 24 20 Проверить гипотезу о нормальном распределении случайной величины Х. 21 13 7



