Круги Эйлера
advertisement
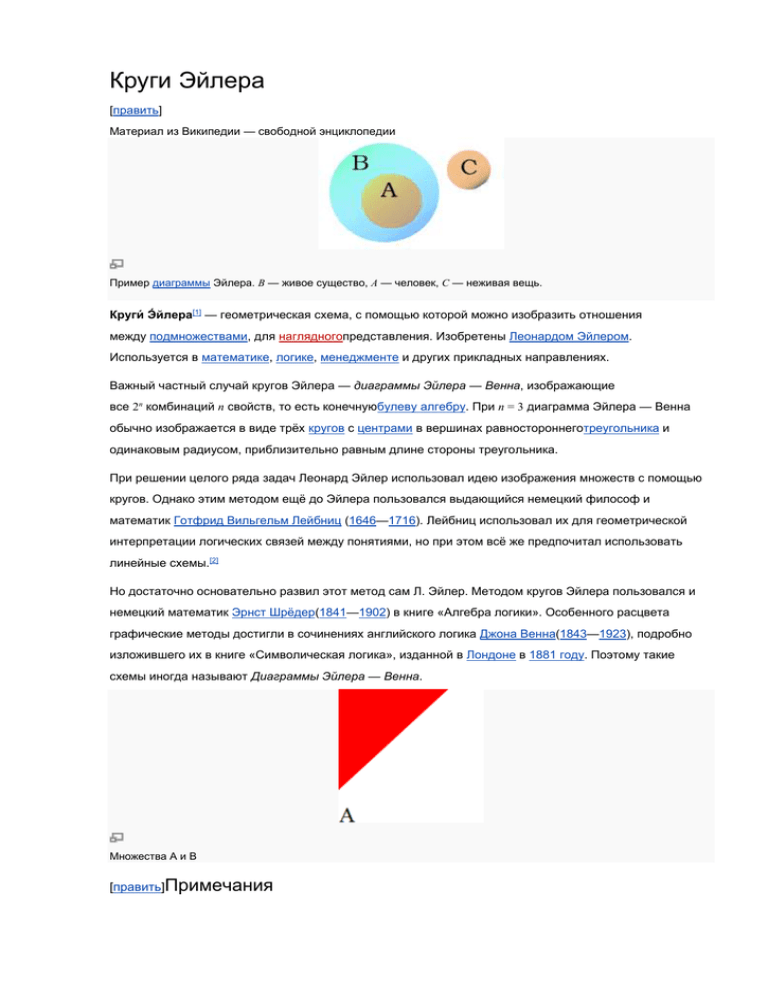
Круги Эйлера [править] Материал из Википедии — свободной энциклопедии Пример диаграммы Эйлера. B — живое существо, A — человек, C — неживая вещь. Круги́ Э́йлера[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядногопредставления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях. Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 2n комбинаций n свойств, то есть конечнуюбулеву алгебру. При n = 3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннеготреугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника. При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.[2] Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер(1841—1902) в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна(1843—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна. Множества А и B [править]Примечания 1. ↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью. Эйлер, Леонард [править] Материал из Википедии — свободной энциклопедии В Википедии есть статьи о других людях с фамилией Эйлер. Леонард Эйлер нем. Leonhard Euler Портрет, выполненный ЭмануэлемХандманном (1756) Дата рождения: 4 (15) апреля 1707 Место рождения: Базель, Швейцария Дата смерти: Место смерти: Страна: 7 (18) сентября 1783 (76 лет) Санкт-Петербург, Российская империя Швейцария Научная сфера: Альма-матер: Научный руководитель: Математика, механика,физика, астрономия Базельский университет Иоганн Бернулли Леона́рдЭ́йлер (нем. Leonhard Euler; 4 (15) апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург,Российская империя) — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Эйлер — автор более чем 800 работ[1] по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. В 1726 году он был приглашён работать в Санкт-Петербург, куда переехал годом позже. С 1731 по 1741, а также с 1766 года был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь одновременно почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академикиматематики (С. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.[2] Круги Эйлера – задачи на пересечение или объединение множеств Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче. "Обитаемый остров" и "Стиляги" Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»? Решение Чертим два множества таким образом: 6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров». 11 – 6 = 5 – человек, которые смотрели только «Стиляги». Получаем: Ответ. 5 человек смотрели только «Стиляги». Любимые мультфильмы Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»? Решение В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж: Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем: 21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов». 13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок». Получаем: 38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны». Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны». «Мир музыки» В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры? Решение Изобразим эти множества на кругах Эйлера. Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры: Ответ: 6 покупателей купили диски и Максим, и Земфиры. Гарри Поттер, Рон и Гермиона На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон? Решение Учитывая условия задачи, чертеж будет таков: Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон. Пионерский лагерь В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом? Решение Изобразим множества следующим образом: 70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек. Ответ. 5 человек заняты только спортом. Экстрим Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах? Решение Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде. Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде. Кофейные круги Эйлера Круги Эйлера помогают изобразить отношения между разными множествами. Кофейная схема наглядно показывает популярные кофейные напитки в соотношении с разными компонентами. Круги Эйлера Примеры решения задач. Задача. В классе 25 учащихся. Из них 5 человек не умеют играть ни в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 — в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы? Решение. 25-5=20 человек играют и шашки и в шахматы, все 20 человек играют в шахматы, из них 18 играют в шашки. Следовательно, 18 человек играют и шашки и в шахматы. Задачи для самостоятельного решения. 2. Каждый из 35 пятиклассников является читателем по крайней мере одной из двух библиотек: школьной и районной. Из них 25 учащихся берут книги в школьной библиотеке, 20 — в районной. Сколько из пятиклассников: а) не являются читателями школьной библиотеки; б) не являются читателями районной библиотеки; в) являются читателями только школьной библиотеки; г) являются читателями только районной библиотеки; д) являются читателями обеих библиотек? 3. В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть вих: а) пересечении; б) объединении? 4. Каждый ученик в классе изучает либо английский, либо французский язык, либо оба этих языка. Английский язык изучают 25 человек, французский — 27 человек, а тот и другой —18 человек. Сколько всего учеников в классе? 5. На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. Найдите площадь листа. 6. В бригаде полеводов 25 человек. Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? 7. В детском саду 52 ребенка. Каждый из них любит либо пирожное, либо мороженое, либо и то, и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое? 8. Сколько в классе учащихся, если известно, что лыжным спортом увлекаются 28 человек, отличников в классе — 12, причем отличниковспортсменов, увлекающихся лыжами, — 10? 37 школьников из ученической производственной бригады изъявили желание летом работать на уборке зерновых. Каждый из них имеет права для работы на тракторе или на комбайне, а некоторые могут работать и на тракторе, и на комбайне. Сколько школьников могут работать и на тракторе, и на комбайне, если известно, что трактором хорошо овладели 23 человека, а комбайном — 31 человек? 9. 1. На стол бросили две салфетки 10 см × 10 см, как показано на рисунке. Они покрыли площадь стола, равную 172 см 2 . Какова площадь их перекрытия? 2. В поход ходили 80% учеников класса, а на экскурсии было 60% класса, причём каждый был в походе или на экскурсии? Сколько процентов класса были и там, и там? 3. В классе 35 учеников. 20 из них занимаются в математическом кружке, 11 — в биологическом, а 10 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией? 4. Сколько существует целых положительных чисел, меньших 100, которые: а) делятся одновременно на 2 и на 3; б) делятся на 2, но не на 3; в) делятся на 3, но не на 2; г) делятся на 3 или на 2; д) не делятся ни на 2, ни на 3? 5. Большая группа туристов выехала в заграничное турне. Из них владеет английским языком 28 человек, французским — 13, немецким — 10, английским и французским — 8, французским и немецким — 5, английским и немецким — 6, всеми тремя языками — двое, а 41 человек не владеет ни одним из трёх языков. Сколько всего туристов? 6. А — подмножество множества натуральных чисел, каждый элемент которого есть число, кратное или 2, или 3, или 5. Найдите число элементов в множестве A, если среди них 70 чисел, кратных 2; 60 чисел, кратных 3; 80 чисел, кратных 5; 32 числа кратных 6; 35 чисел, кратных 10; 38 чисел, кратных 15; 20 чисел, кратных 30. 7. Каждый из трёх игроков записывает 100 слов, после чего записи сравнивают. Если слово встретилось хотя бы у двоих, то его вычёркивают из всех списков. Могло ли случиться так, что у первого игрока осталось 61 слово, у второго — 80 слов, а у третьего — 82 слова? Для домашнего обдумывания 8. Каких натуральных чисел от 1 до 2006 больше: кратных 8, но не кратных 9, или тех, которые кратны 9, но не кратны 8? 9. Три ученика решили вместе 100 задач, при этом каждый из них решил ровно 60 задач. Будем называть задачу, которую решили все трое, лёгкой, а задачу, которую решил только один из них, — трудной. На сколько больше трудных задач, чем лёгких?





