Летнее задание по математике для учащихся 10 класса
advertisement

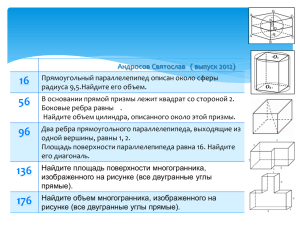
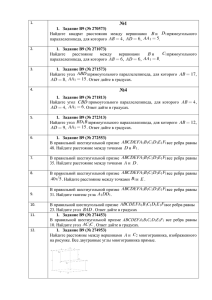
Летнее задание по математике для учащихся 10 класса по материалам сайта http://mathege.ru ТЕМА 1: Элементы тригонометрии. Повторить: радианная мера угла; Определение синуса, косинуса, тангенса, котангенса угла Знаки синуса, косинуса, тангенса, котангенса угла Зависимость между синусом, косинусом, тангенсом, котангенсом одного и того же угла Тригонометрические функции противоположных углов Формулы сложения Синус, косинус, тангенс, котангенс двойного угла Формулы приведения Синус, косинус, тангенс, котангенс половинного угла Сумма и разность синусов, сумма и разность косинусов Решение простейших тригонометрических уравнений (ФОРМУЛЫ РЕШЕНИЙ!) 1. Найдите значение выражения: , , , , , , , , , , , , , , 2. Найдите , если и 3. Найдите , если и 4. Найдите , , если 5. Найдите значение выражения 6. Найдите значение выражения , . . и . . . 7. Найдите значение выражения 8. Найдите , если 9. Найдите , если . , если 10. Найдите . , если 11. Найдите . , если . . 12. Найдите значение выражения 13. Решить уравнения: , если . а) sin2 x = б) 3sin2 x sin x 2cos x 3sin 2x в) cosх 4cos +1 = 0 г) sin 2x 2 cos2 x д) 7cos(х е) tg x ctg ( sin x + 1= 0 + x) + 2 = 0 ж) 6sin2 x + sin xcos x cos2 x =0 з) sin 3x + cos11х = 0 и) ctg2 x 2ctg x к) cos(х cos x =1 ТЕМА 2: Степень. Показательная функция. Степенная функция. Повторить: Арифметический корень натуральной степени Определения степени с натуральным, целым, рациональным и действительным показателем Свойства степени с натуральным, целым, рациональным и действительным показателем Показательная функция, её свойства и график Степенная функция, её свойства и график 1. Найдите значение выражения , , ., , , , , , , , , , , 2. Найдите корень уравнения ., , , , , 3. Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них. 4. Найдите корень уравнения . 5. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. ТЕМА 3: Логарифмы и их свойства. Логарифмическая функция. Повторить: Определение логарифма Свойства логарифмов Логарифмическая функция, её свойства и график 1. Найдите корень уравнения , , , , 2. Решите уравнение ответе укажите меньший из них. , . Если уравнение имеет более одного корня, в ______________________________________ 1. Решите уравнения: а)3х·2х = 8х+3 , б)32х+4·3х-5 = 0, в) 22х - 8х+1 = 0, г) 32х+4 -11·9х = 210, д) 4х - 3·2х +2 = 0 е) 2х+3 - 2х+2 - 2х = 48 ж) 9х - 8·3х = 9 з) 2х - 20,5х+1 - 8 = 0 и) log3(х2-3) = log3(2х) к) logх+1(х2+3х-7) = 2 , л) lg2(x+1)+10 = 11lg(x+1) м) log16(0,5х-1,5) = 0,25 н) ln(е2+2х-3) = 2 о) log2(14х) = log27 + 2 п) р) ln(х3-7х+2sinx+3) = ln(х3-7х+2sinx-4) ТЕМА 3: Многогранники. Повторить: Определения, свойства, формулы для вычисления боковой и полной поверхности призмы, пирамиды, виды многогранников (правильный, произвольный) 1. Найдите расстояние между вершинами и прямоугольного параллелепипеда, для которого , , . 2. Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах. 3. Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах. 4. В правильной шестиугольной призме все ребра равны . Найдите расстояние между точками и . 5. В правильной шестиугольной призме все ребра равны 30. Найдите тангенс угла . 6. Найдите расстояние между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. 7. Найдите расстояние между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. 8. Найдите тангенс угла многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. 9. В правильной треугольной пирамиде — середина ребра , — вершина. Известно, что ,а . Найдите площадь боковой поверхности. 10. В правильной треугольной пирамиде — середина ребра , — вершина. Известно, что , а площадь боковой поверхности равна 36 . Найдите длину отрезка . 11. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 12. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Площадь поверхности этого параллелепипеда равна 136. Найдите третье ребро, выходящее из той же вершины. 13. Площадь поверхности куба равна 32. Найдите его диагональ. 14. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 7. 15. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 24 и 6. Площадь поверхности параллелепипеда равна 768. Найдите его диагональ. 16. Если каждое ребро куба увеличить на 2, то его площадь поверхности увеличится на 144. Найдите ребро куба. 17. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 25 и 60, и боковым ребром, равным 25. 18. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 8, а площадь поверхности равна 416. 19. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы. 20. Стороны основания правильной четырехугольной пирамиды равны 84, боковые ребра равны 58. Найдите площадь поверхности этой пирамиды.