КИМ простейшие тригонометрические уравнения

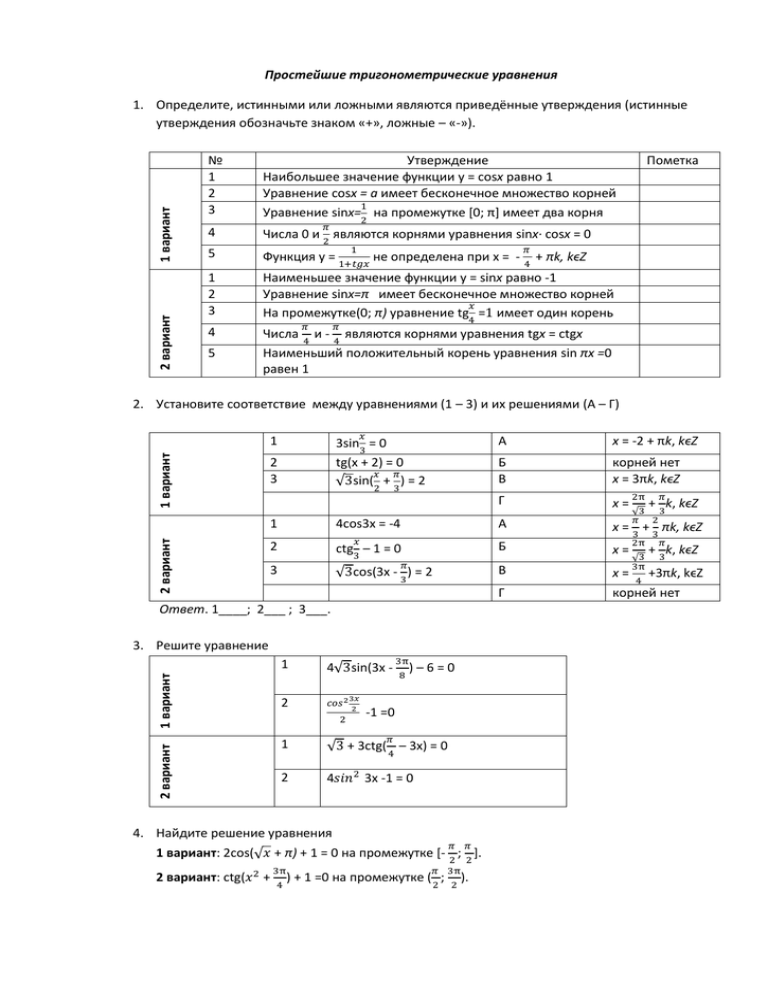
Простейшие тригонометрические уравнения
2 вариант
1 вариант
1. Определите, истинными или ложными являются приведённые утверждения (истинные
утверждения обозначьте знаком «+», ложные – «-»).
№
1
2
3
Утверждение
Наибольшее значение функции y = cosx равно 1
Уравнение cosx = a имеет бесконечное множество корней
1
Уравнение sinx= на промежутке [0; π] имеет два корня
4
Числа 0 и 2 являются корнями уравнения sinx· cosx = 0
5
Функция y = 1+𝑡𝑔𝑥 не определена при x = -
1
2
3
Наименьшее значение функции y = sinx равно -1
Уравнение sinx=π имеет бесконечное множество корней
𝑥
На промежутке(0; π) уравнение tg4 =1 имеет один корень
4
Числа
5
Наименьший положительный корень уравнения sin πx =0
равен 1
2
𝜋
1
𝜋
4
и-
Пометка
𝜋
4
𝜋
4
+ πk, kϵZ
являются корнями уравнения tgx = ctgx
2. Установите соответствие между уравнениями (1 – 3) и их решениями (А – Г)
𝑥
2 вариант
1 вариант
1
3sin = 0
3
tg(x + 2) = 0
𝑥 𝜋
√3sin( + ) = 2
2
3
2
3
А
x = -2 + πk, kϵZ
Б
В
корней нет
x = 3πk, kϵZ
Г
x=
2π 𝜋
+ k, kϵZ
√3 3
𝜋 2
= 3 + 3 πk, kϵZ
2π 𝜋
= 3 + 3 k, kϵZ
√
3π
= +3πk, kϵZ
4
1
4cos3x = -4
А
x
2
𝑥
ctg3
Б
x
В
x
Г
корней нет
3
–1=0
√3cos(3x
𝜋
- 3)
=2
Ответ. 1____; 2___ ; 3___.
2 вариант
1 вариант
3. Решите уравнение
1
4√3sin(3x -
2
𝑐𝑜𝑠2
2
3𝑥
2
3π
)
8
–6=0
-1 =0
𝜋
1
√3 + 3ctg( 4 – 3x) = 0
2
4𝑠𝑖𝑛2 3x -1 = 0
4. Найдите решение уравнения
𝜋 𝜋
2 2
𝜋 3π
( 2 ; 2 ).
1 вариант: 2cos(√𝑥 + π) + 1 = 0 на промежутке [- ; ].
2 вариант: ctg(𝑥 2 +
3π
)
4
+ 1 =0 на промежутке
5. Найдите наименьший положительный корень уравнения
𝜋𝑥
12
1 вариант: а) cos2πx = 1;
2 вариант: а) sin(πx + 3π) =
б) tg( ) = √3.
1
2
,
б) ctg2πx = 1.
6. Найдите наибольший отрицательный корень уравнения
1 вариант: а) sin
𝜋𝑥
6
𝜋𝑥
= 0;
б) ctg(- 12 - 3 π) = 1.
2 вариант: а) sinπx ·cosπx = 0;
𝜋𝑥
б) tg( 3 ) =
√3
.
3
Тригонометрические уравнения, приводимые к квадратным
1. Приведите уравнение к квадратному относительно одной из тригонометрических
функций
2− 𝑐𝑜𝑠2𝑥
+ 2 =0.
𝑐𝑜𝑠𝑥
6
1
б)
+
=1
6−𝑐𝑡𝑔𝑥 𝑡𝑔𝑥
1 вариант: а) 2𝑐𝑜𝑠 2 x + 5sinx – 4 = 0; б)
2 вариант: а) 3cos2x – 7sinx = 0;
= 12ctgx.
2. Какие из приведённых уравнений не имеют решений? Ответ объясните.
1вариант: а) 𝑠𝑖𝑛2 x + 8sinx + 15 = 0; б) 𝑡𝑔2 2x – 6tg2x + 9 = 0
𝜋
4
𝜋
4
с𝑡𝑔2 (x - )– 8сtg(x - ) - 48 = 0;
2вариант: а)
б) 𝑐𝑜𝑠 2
𝑥
2
𝑥
2
- 12cos – 13 =0
3. Установите соответствие между уравнениями (1 – 5) и их решениями (А – Е)
Вариант 1
𝜋
1
1
А
x = ± + πk, kϵZ
𝑡𝑔2 x - = 0
3
3
2
3
2𝑠𝑖𝑛2x + 3sinx – 2 = 0
𝑥
𝑥
𝑐𝑜𝑠 2 2 + 5cos2 – 14 =0
4
8𝑐𝑜𝑠 2 2x – 6cos2x – 5 = 0
5
2𝑠𝑖𝑛2 2 = 12
𝑥
1
Б
В
корней нет
𝜋
X =(−1)𝑘 · 6 + πk, kϵZ
Г
x=
Д
x=
Е
x=
А
x = ± 3 + πk, kϵZ
2π 𝜋
+ k, kϵZ
√3 3
2𝜋
± 3 + 2πk, kϵZ
𝜋
± 6 + πk, kϵZ
Ответ. 1____; 2_____; 3____; 4_____; 5____.
Вариант 2
1
1
𝑐𝑜𝑠 2 x - 2 = 0
𝜋
𝜋
4
2
2𝑠𝑖𝑛22x – 7sin2x + 6 = 0
Б
x = ± + πk, kϵZ
3
𝑡𝑔2 x - 3= 0
В
x=
4
5
√2 𝑐𝑜𝑠 2 x + cosx – √2 = 0
𝑡𝑔2 x – 6tgx + 9 = 0
Г
Д
x = arctg3 + πk, kϵZ
Е
корней нет
Ответ. 1____; 2_____; 3____; 4_____; 5____.
𝜋
4
+ πk, kϵZ
𝜋
x = ± 4 +2πk, kϵZ