Задание 1. Для заданного сечения, состоящего из стандартных равнополочных уголков A, I

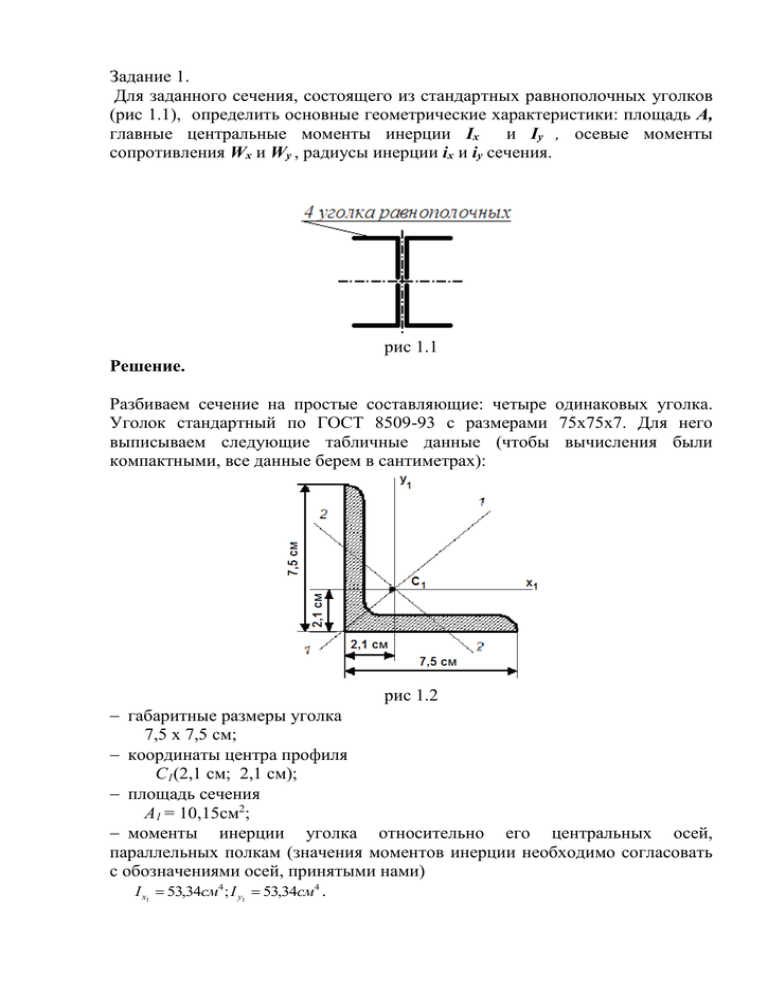
Задание 1.
Для заданного сечения, состоящего из стандартных равнополочных уголков
(рис 1.1), определить основные геометрические характеристики: площадь A,
главные центральные моменты инерции Ix
и Iy , осевые моменты
сопротивления Wx и Wy , радиусы инерции ix и iy сечения.
рис 1.1
Решение.
Разбиваем сечение на простые составляющие: четыре одинаковых уголка.
Уголок стандартный по ГОСТ 8509-93 с размерами 75х75х7. Для него
выписываем следующие табличные данные (чтобы вычисления были
компактными, все данные берем в сантиметрах):
рис 1.2
 габаритные размеры уголка
7,5 х 7,5 см;
 координаты центра профиля
С1(2,1 см; 2,1 см);
 площадь сечения
А1 = 10,15см2;
 моменты инерции уголка относительно его центральных осей,
параллельных полкам (значения моментов инерции необходимо согласовать
с обозначениями осей, принятыми нами)
I x  53,34см4 ; I y  53,34см4 .
1
1
Делаем чертеж всего сечения в масштабе (рисунок 1.1). Переносим на чертеж
центры С1 ,С2 ,С3 и С4 всех уголков.
Делаем чертеж всего сечения в масштабе. Переносим на чертеж центры
С1,С2,С3 и С4 всех уголков.
Определяем характеристики всего сечения.
рис 1.3
Габаритные размеры сечения 1515см.
Центр всего сечения С расположен на пересечении осей симметрии сечения.
Площадь сечения А=А1+А2 +А3+А4 = 10,15 + 10,15 + 10,15 + 10,15 = 40,6см2.
Проводим координатные оси хСу , х1С1у1 , х2С2у2, х3С3у3, х4С4у4 и вычисляем
расстояния между параллельными осями:
горизонтальными: а1 =а2 = а3 = а4 = 7,5 - 2,1 = 5,4 см;
вертикальными: b1 =b2 = b3 = b4 = 2,1 см;
Вычисляем моменты инерции всего сечения по формулам для параллельных
осей:


I x   I xi  Ai ai2  I x1  A1a12  I x2  A2 a 22  I x3  A3 a32  I x4  A4 a 42 


 4  53,34  10,15  5,4 2  1397,256см 4


I y   I yi  A b  I y1  A1b12  I y2  A2 b22  I y3  A3b32  I y4  A4 b42 

2
i i

 4  53,34  10,15  2,12  392,406см 4
I xy  0 – так как оси Сх и Сy является осями симметрии всего сечения. Из
этого следует, что оси хСу являются главными осями инерции сечения, а
полученные значения моментов инерции – главными моментами инерции.
Вычисляем моменты сопротивления сечения:
I
1397,256
Wx= x =
= 186,3 см3;
7,5
y max
Iy
392,406
Wy=
=
= 52,32 см3;
7,5
xmax
Вычисляем радиусы инерции сечения:
ix=
iy=
Ix
1397,256
=
= 5,9 см;
40,6
A
Iy
A
=
392,406
= 3,1 см.
40,6
Задание 2.
Плоская ферма (рисунок 2.1) состоит из двух стержней круглого сечения.
Соединение стержней между собой и с основанием шарнирное. Материал
всех деталей – сталь Ст3. Определить из расчета на прочность:
 диаметры D1 и D2 сечений стержней фермы;
 размеры шарнирного соединения (диаметр d цилиндрического пальца и
толщину t головки), предполагая все шарниры одинаковыми.

F  125кН , L  0,8 м ,   60 0 ,   30 0 и   0 0
Решение
Расчет на растяжение и сжатие
Рис 2.1 Схема фермы.
Определяем продольные силы в стержнях методом сечений. Для этого
вырезаем узел В двумя секущими плоскостями перпендикулярными осям
стержней – именно в поперечных сечениях возникают максимальные
нормальные напряжения (рисунок 2.2).
рис 2.2
В полученных сечениях наносим векторы продольных (нормальных) сил N1 и
N2 по направлению от сечений и составляем уравнения равновесия узла в
виде сумм проекций сил на любые две взаимно перпендикулярные оси х и у:
3
1
N1  N 2  0
2
2
1
3
 Fy   N1 cos 60 0  N 2 cos 30 0  F   2 N1  2 N 2  125  0
F
x
 N1 sin 60 0  N 2 sin 30 0 
Решая совместно эти уравнения, получим значения продольных сил:
N1 = 62,5кН; N2 = − 108,25 кН.
Продольная сила N1 положительная, а сила N2 - отрицательная,
следовательно, стержень 1 работает на растяжение, а стержень 2 на сжатие.
N
В условие прочности при растяжении и сжатие
 []р подставляем
A
выражение площади круглого сечения A 
d12
4
и из полученного неравенства
определяем диаметр сечения стержня 1.
D
4N
 [ ] p
Из приложения Б выписываем величину допускаемого напряжения для стали
Ст3 – []p =125МПа и вычисляем диаметры сечения стержней:
D1 
4 N1
4  62,5  10 3

 0,0252 м  25,2 мм
 [ ] p
3,14  125  10 6
D2 
4N 2

 [ ] p
4  102,25  10 3
 0,0332 м  33,2 мм
3,14  125  10 6
Полученные значения диаметров округляем до ближайших больших
значений из рядов нормальных линейных размеров (приложение В).
Окончательно принимаем: d2 = 34 мм, d1 = 26 мм.
Расчет на устойчивость
Для круглого сечения выписываем расчетные формулы геометрических
характеристик: площадь A 
D 2
4
; минимальный момент инерции I min 
минимальный радиус инерции imin 
D 4
64
;
l
D
. По формуле  
определяем в
4
imin
общем виде гибкость

l
imin

1  l  4 4l
 ,
D
D
где  =1 для двухшарнирного закрепления .
Выражение площади подставляем в условие устойчивости
полученного неравенства выражаем диаметр сечения:
D
4N
 сж
N
A
   сж и из
.
Для стали Ст3 – []сж=[]р= 125МПа.
В формуле два неизвестных: диаметр D и коэффициент , решаем способом
последовательных приближений.
Расчет первого стержня. N1= 62,5 кН; l1 
h
800  2

 923,76 мм
0
sin 60
3
Первый шаг приближений:

задаем 1=0,5 (можно задать любое значение из интервала 01);

вычисляем по формуле диаметр
D1 
4  62,5  10 3
 0,0357 м  35,7 мм ;
3,14  0,5  125  10 6

округляем полученное значение до ближайшего большего из ряда
нормальных размеров: D1  36 мм ;

вычисляем гибкость  
4  l1
 103 ;
D1
из приложения Г определяем коэффициент , соответствующий гибкости
 = 103: 1* 0,576;

сравниваем значения 1 = 0,5 на входе в расчет и 1*=0,576 на выходе:

разность

0,576  0,5
 100%  15,2%
0,5
допустимую погрешность 5%.
,
что
значительно
превосходит
Расчет повторяем в той же последовательности со значением коэффициента
, равным среднему арифметическому на первом шаге:  ср 
0,576  0,5
 0,538 .
2
Второй шаг приближений:
 принимаем 2 = 0,538;
 вычисляем D1 
4  62,5  10 3
 0,0344 м  34,4 мм ;
3,14  0,538  125  10 6
 полученное значение соответствует стандартному D1 = 36 мм;
 гибкость  
4  l1
 103 ;
D1
 значение коэффициента на выходе 2*0,576;
 разность  
0,576  0,538
 100%  7,1% . Выше 5%.
0,538
Третий шаг приближений:
 принимаем  3 
 вычисляем D1 
0,576  0,538
 0,557 ;
2
4  62,5  10 3
 0,0338 м  33,8 мм ;
3,14  0,557  125  10 6
 полученное значение соответствует стандартному D1 = 34 мм;
 гибкость  
4  l1
 109 ;
D1
 значение коэффициента на выходе 2*0,528;
 разность  
0,557  0,528
 100%  5,2% . Выше 5%.
0,557
Четвертый шаг приближений:
 принимаем  3 
 вычисляем D1 
0,557  0,528
 0,543 ;
2
4  62,5  10 3
 0,0342 м  34,2 мм ;
3,14  0,543  125  10 6
 полученное значение соответствует стандартному D1 = 34 мм;
 гибкость  
4  l1
 109 ;
D1
 значение коэффициента на выходе 2*0,528;
 разность  
0,543  0,528
 100%  2,7% .
0,543
На этом способ последовательных приближений заканчиваем с результатом
D1 = 34 мм,  = 109.
Проверяем первый стержень по коэффициенту запаса устойчивости. Для
этого вычисляем критическую силу. Гибкость  = 109 > 100, поэтому
используем формулу Эйлера

 2 EI min 3,14 2  2  1011  65597,24  10 12
F


 151,7 кН
 кр
l1 2
1  0,92376 2

,

 2 E 3,14 2  2  1011

 166 МПа
 кр  2 
109 2
D 4
Для стали Ст3, I min  1  65597,24 мм 4 , E  2  1011 Па
64
F
Коэффициент запаса устойчивости n y  кр  2,43 .
N1
Нормативное значение коэффициента запаса устойчивости для стальных
конструкций nу=1,83,0. Полученное значение фактического коэффициента
запаса устойчивости входит в нормативный интервал.
Итак, диаметр сечения первого стержня D1 = 34 мм.
Расчет второго стержня. N2= 108,25 кН; l 2 
h
 800  2  1600 мм
sin 30 0
Первый шаг приближений:

задаем 1=0,5 (можно задать любое значение из интервала 01);

вычисляем по формуле диаметр
D2 
4  108,25  10 3
 0,047 м  47 мм ;
3,14  0,5  125  10 6

округляем полученное значение до ближайшего большего из ряда
нормальных размеров: D2  48 мм ;

вычисляем гибкость  
4  l2
 133 ;
D2
из приложения Г определяем коэффициент , соответствующий гибкости
 = 133: 1* 0,39;

сравниваем значения 1 = 0,5 на входе в расчет и 1*=0,39 на выходе:

разность  
0,5  0,39
 100%  22% , что значительно превосходит допустимую
0,5
погрешность 5%.
Расчет повторяем в той же последовательности со значением коэффициента
, равным среднему арифметическому на первом шаге:  ср 
0,39  0,5
 0,445 .
2
Второй шаг приближений:
 принимаем 2 = 0,445;
 вычисляем D2 
4  108,25  10 3
 0,0498 м  49,8 мм ;
3,14  0,445  125  10 6
 полученное значение соответствует стандартному D2 = 50 мм;
 гибкость  
4  l2
 128 ;
D2
 значение коэффициента на выходе 2*0,41;
 разность  
0,445  0,41
 100%  7,9% . Выше 5%.
0,445
Третий шаг приближений:
 принимаем  3  0,428 ;
 вычисляем D2 
4  108,25  10 3
 0,0508 м  50,8 мм ;
3,14  0,428  125  10 6
 полученное значение соответствует стандартному D2 = 50 мм;
 гибкость  
4  l2
 128 ;
D2
 значение коэффициента на выходе 2*0,41;
 разность  
0,428  0,41
 100%  4,2% .
0,428
На этом способ последовательных приближений заканчиваем с результатом
d2 = 50 мм,  = 128.
Проверяем первый стержень по коэффициенту запаса устойчивости. Для
этого вычисляем критическую силу. Гибкость  = 121 > 100, поэтому
используем формулу Эйлера

 2 EI min
F

 298,65кН
 кр
l 2 2

,

2
 E

 кр  2  134,82 МПа
D 4
Для стали Ст3, I min  2  387323,08 мм 4 , E  2  1011 Па
64
F
Коэффициент запаса устойчивости n y  кр  2,76 .
N2
Нормативное значение коэффициента запаса устойчивости для стальных
конструкций nу=1,83,0. Полученное значение фактического коэффициента
запаса устойчивости входит в нормативный интервал.
Итак, диаметр сечения второго стержня D2 = 53 мм.
Расчет цилиндрического шарнира
Расчет шарнира первого стержня.
Тяга соединяется с кронштейном (рис 2.3) при помощи цилиндрического
пальца.
Палец работает на срез в двух плоскостях, и смятие от действия на него тяги
и кронштейна (рисунок 2.4).
Срезающая сила Q  N1  62,5кН . Общая площадь среза пальца
 d 2 
Aср   1 k ,
 4 
где d1 – диаметр сечения пальца;
k  2 – число плоскостей среза пальца.
С учетом этих значений из условия прочности на срез
d1 
Q
 [ ]ср получаем:
Aср
4 N1
4  62,5  10 3

= 0,023 м  23 мм ,
k[ ]cp
3,14  2  75  10 6
где [ ]ср  75МПа – допускаемое напряжение на срез для стали Ст3.
Полученное значение диаметра округляем до нормального размера d1  24 мм .
Смятие пальца происходит по половине цилиндрической поверхности
(рисунок 2.5), площадь ее проекции Aсм  d1  t 1 , тогда из условия прочности
на смятие
t1 
Q
 [ ]см
Асм
Q
62,5  10 3

 0,0137 м  13,7 мм
d1  [ ]см 0,024  190  10 6
где [ ]см  190МПа для стали Ст3.
Принимаем в соответствии с рядом нормальных размеров t1  14 мм . Из
условия равнопрочности толщина планок кронштейна должна быть в 2 раза
меньше:
t1
 7 мм .
2
Расчет шарнира второго стержня.
Тяга соединяется с кронштейном (рис 2.6) при помощи цилиндрического
пальца.
Палец работает на срез в двух плоскостях, и смятие от действия на него тяги
и кронштейна (рисунок 2.7).
Срезающая сила Q  N 2  108,25кН . Общая площадь среза пальца
 d 2 
Aср   2 k ,
 4 
где d 2 – диаметр сечения пальца;
k  2 – число плоскостей среза пальца.
С учетом этих значений из условия прочности на срез
d1 
Q
 [ ]ср получаем:
Aср
4N 2
4  108,25  10 3

 0,0303 м  30,3 мм ,
k[ ]cp
3,14  2  75  10 6
где [ ]ср  75МПа – допускаемое напряжение на срез для стали Ст3.
Полученное значение диаметра округляем до нормального размера d 2  30 мм .
Смятие пальца происходит по половине цилиндрической поверхности
(рисунок 2.5), площадь ее проекции Aсм  d 2  t 2 , тогда из условия прочности
на смятие
t2 
Q
 [ ]см
Асм
Q
108,25  10 3

 0,019 м  19 мм
d 2  [ ]см 0,03  190  10 6
где [ ]см  190МПа для стали Ст3.
Принимаем в соответствии с рядом нормальных размеров t 2  19 мм . Из
условия равнопрочности толщина планок кронштейна должна быть в 2 раза
меньше:
t2
 9,5 мм .
2
Задание 3.
Вал (рисунок 3.1) приводится во вращение от двигателя через муфту (муфта
втулочная). Вал приводит в движение через шкивы 1 и 2 два механизма
мощностью соответственно P1  25кВт и P2  15кВт .Вал делает n  500
оборотов в минуту. Пренебрегая изгибом вала, определить диаметр D его
сечения из расчета на прочность и жесткость при кручении. Допускаемый
относительный угол закручивания вала принять [ ]  0,5
град
. Определить
м
также диаметры d штифтов (болтов) и толщину t втулки (фланца) муфты из
расчета на прочность при срезе и смятии. Считать, что все детали
изготавливаются из Сталь 20.
Рис 3.1 Схема привода вала и муфты.
Решение
Расчет на кручение
Рис 3.2
Находим моменты, которые передаются на вал через шкивы, по формуле
М 
P

, где  
n
30

3,14  500
 52,3c 1 – угловая скорость вращения:
30
25  10 3
 478Н  м

52,3
P2 15  10 3
М2 

 286,8Н  м

52,3
М1 
P1

Момент на ведущем шкиве, очевидно, равен
M 0   M i  M 1  M 2  478  286,8  764,8Н  м .
На расчетной схеме вала (рисунок 3.3) момент М0 должен иметь направление
обратное направлению моментов на ведомых шкивах.
Разбиваем вал на участки I,II,III и строим эпюру внутреннего крутящего
момента ТК методом сечений (рисунок 3.3).
Проводим секущую плоскость на участке I. Правую от сечения часть вала
отбрасываем. Для сохранения равновесия в сечении прикладываем
внутренний момент ТК1 , направляя его против часовой стрелки со стороны
внешней нормали к сечению. Составляем уравнение равновесия левой части:
 M  TK1  M 0  0 ,
откуда определяем TK1  M 0  764,8Нм . Очевидно, что в любом сечении на
первом участке TK1  764,8Нм  const . Строим график константы на первом
участке и проводим вертикальную штриховку.
Рассекаем вал плоскостью на участке II, отбрасываем также правую часть,
момент ТК2 направляем против часовой стрелки, составляем уравнение
равновесия:
 M  TK 2  M 0  M1  0 ,
из которого TK 2  M 0  M 1  286,8Нм . Строим график на втором участке.
При рассмотрении участка III выгоднее отбрасывать левую от сечения
часть.
На третьем участке  M  TK 3  0 , откуда TK 3  0 .
Рис 3.3
Полученная эпюра крутящего момента наглядно показывает, как нагружен
вал по участкам.
Рассчитываем вал на прочность. В условие прочности при кручении
TK
 [ ] кр подставляем формулу для полярного момента сопротивления
W
W 
D 3
и выражаем диаметр:
16
16Т K
.
D3
 [ ]кр
При расчете гладкого вала (одного диаметра по всей длине) в качестве ТК
берется с эпюры максимальное абсолютное значение крутящего момента:
TK  764,8Нм
Выписываем значение кр=105МПа для стали 20 и вычисляем диаметр вала:
D3
16Т K
16  764,8
3
 0,0334 м  33,4 мм
 [ ]кр
3,14  105  10 6
Округляем, полученные данные до D  34 мм
Рассчитываем вал на жесткость. В условие жесткости при кручении
TK 180 0


   подставим формулу для полярного момента инерции
GI 

I 
D 4
32
и выразим диаметр:
D4
32  180  Тк
,
 2  G  [ ]
где G = 81010Па – значение модуля сдвига для стали, TK - максимальный
скручивающий момент.
Определяем диаметр D  4
32  180  Тк
32  180  764,8
4
 0,0578 м  57,8 мм
2
  G  [ ]
3,14 2  8  1010  0,5
В расчете принято значение допускаемого относительного угла закручивания
=0,5град/м.
Округляем: D  60 мм
Расчет втулочной муфты
Штифт (рисунок 3.4) работает на срез и смятие. Срезающая сила Q равна
окружному усилию на поверхности вала:
TK1 2TK1 2  764,8


 25493H - усилие для подшипника А, где M - это
R
D
60  10 3
момент на участке I, а D - это максимальный из диаметров, полученных при
QA 
расчете на кручение.
Усилие для подшипника B не вычисляем, поскольку на участке III
скручивающий момент равен 0.
Площадь среза штифта Aср 
d 2
k , где k = 2.
4
Q
Из условия прочности на срез A  [cp
Acp
d
4Q
4  25493

 0,0138 м  13,8 мм ,
k[ ]cp
3,14  2  85  10 6
где ср=85МПа для стали 20.
Полученное значение диаметра штифта округляем до нормального размера:
d  14 мм
Толщину стенки муфты t определяем из условия прочности на смятие
Q
  cм , подставив в него выражение Aсм  t  d  k :
Асм
Q
25943
t

 0,0043 м  4,3 мм ,
dk  см 0,014  2  210  10 6
где см= 210МПа для стали 20.
Принимаем толщину стенки муфты t = 5мм.
Задание 4
Для заданных двух схем балок построить эпюры изгибающего момента МХ и
поперечной силы Q и определить:

для схемы (а) – размеры прямоугольного сечения деревянной балки при
соотношении сторон
h
 1,5 и допускаемых напряжениях на изгиб изг =
b
8МПа. Проверить балку по касательным напряжениям, приняв значение
допускаемых напряжений для древесины на скалывание ск=1,2МПа;
 для схемы (б) – номер стандартного двутавра из стали
Ст3.
l  1,3 м , F1  1,3kH , q 1  8
kH
kH
, L  2 м , M  7kHм , q  16
м
м
Решение
Расчет консольной балки
Для консольной балки можно не вычислять реакции в заделке, но при
построении эпюр в этом случае на всех участках необходимо рассматривать
только свободный конец балки.
Нумеруем участки на балке I,II,III в порядке их последующего
рассмотрения.
Проводим сечение на участке I. Рассматриваем правую от сечения часть
балки. Длину ее обозначаем z1 , пределы изменения которой на данном
участке 0  z1  0,4l или 0  z1  0,52 м . Записываем уравнение для изгибающего
момента в данном сечении
M X1
q1 z12
  M справа  
 4 z12 .
2
Получено уравнение параболы с ветвями вниз. Находим ее значения на
границах участка:
при z1  0 м M X 2  4  0 2  0кНм ;
при z1  0,4l  0,52 м M X 2  4  0,52 2  1,08кНм ;
Исследуем параболу на экстремум. Берем производную и приравниваем к
нулю:
dM X 1
 8z1  0 , откуда z1  0 м . Полученное значение z1  0 м входит в
dz1
границы данного участка, поэтому парабола здесь имеет максимум. Находим
его значение:
при z1  0 м M X 2  4  0 2  0кНм .
По трем точкам (на границах участка и максимума) проводим график
параболы.
Перерезывающие усилия определяем из уравнения:
Q1 
dM X 1
 8z1 - уравнение прямой.
dz1
при z1  0 м Q1  8  0  0кН ;
при z1  0,52 м Q1  8  0,52  4,16кН ;
Проводим сечение на участке II. Рассматриваем правую от сечения часть
балки. Длину ее обозначаем z 2 , пределы изменения которой на данном
участке 0,4l  z1  0,8l или 0,52 м  z 2  1,04 м . Записываем уравнение для
изгибающего момента в данном сечении
0,4l 

M X 2   M справа  q1  0,4l  z 2 
  4,16z 2  0,26 .
2 

Получено уравнение прямой. Находим ее значения на границах участка:
при z 2  0,52 м M X 2  4,16  0,52  0,26  1,08кНм ;
при z 2  1,04 м M X 2  4,161,04  0,26  3,24кНм ;
По двум точкам (на границах участка) проводим график прямой.
Перерезывающие усилия определяем из уравнения:
Q2 
dM X 2
 4,16кН - const.
dz 2
при z 2  0,52 м Q2  4,16кН ;
при z 2  1,04 м Q2  4,16кН ;
Проводим сечение на участке III. Рассматриваем правую от сечения часть
балки. Длину ее обозначаем z 2 , пределы изменения которой на данном
участке 0,8l  z1  l или 1,04 м  z2  1,3м . Записываем уравнение для
изгибающего момента в данном сечении.
0,4l 

M X 3   M справа  q1  0,4l  z 3 
  F z 3  0,8l   4,16z 3  0,26  1,3z 3  1,04
2 

Получено уравнение прямой. Находим ее значения на границах участка:
при z3  1,04 м M X 3  4,161,04  0,26  1,31,04  1,04  3,24кНм ;
при z 3  1,3м M X 3  4,161,3  0,26  1,31,3  1,04  3,99кНм ;
По двум точкам (на границах участка) проводим график прямой.
Перерезывающие усилия определяем из уравнения:
Q3 
dM X 3
 4,16  1,3  2,86кН - const.
dz 3
при z3  1,04 м Q3  2,86кН ;
при z 3  1,3м Q3  2,86кН ;
Рис 4.3
Определим опасное сечение балки по нормальным напряжениям. Это
сечение, в котором изгибающий момент достигает максимума.
M X max  3,99кНм , Q max  4,16kH .
Определяем размеры сечения балки по нормальным напряжениям. Для
прямоугольного сечения Wx 
тогда из условия прочности
9 Mx
bh 2
,
6
Mx
max
Wx
или при соотношении
h
h3
 1,5 W x 
,
b
9
  изг
9  3,99  10 3
h

 0,165 м  165 мм .
 изг
8  10 6
h
Округляем до h  17см , тогда b 
 11см .
1,5
3
max
3
Проверяем сечение по касательным напряжениям. Для прямоугольного
сечения
h
b
сечения
в
(рисунок 4.4):

Ix 
формуле
Журавского
bh 3
bh h bh 2
; b *  b ; S x*   
;
12
2 4
8
Тогда
x
max
Рис 4.4
b  h2
3
8  3 Q max  3  4,18  10 
 max 
2bh
2  0,11  0,17 =
bh 3
b
12
6
 0,33  10 Па  0,33МПа
Q max 
Это меньше допускаемого значения
ск=1,2МПа, следовательно, условие
прочности
по
касательным
напряжениям выполняется.
Расчет двухопорной балки
Составляем два уравнения равновесия в виде сумм моментов относительно
опор, тогда в каждом уравнении окажется только по одной неизвестной.
Знаки моментов соответствуют правилам теоретической механики:
q  0,5L 
 m A  M  2  M  RB L  0
 mB  M  q  0,5L 1,25L  M  RA L  0
2
решая которые, получим: RA  20кН , R B  4кН .
Чтобы убедиться в правильности вычислений, делаем проверку:
 Y  RA  q  0,5L  RB  20  16  0,5  2  4  0 .
Строим эпюры внутренних силовых факторов МХ и Q.
1
2
Участок I. Слева 0  z1  L
или 0  z1  1м .
Уравнение изгибающего момента
qz12
- уравнение параболы. Ее значения на границах участка:
M X1   M 
2
16  0 2
при z1  0 M X1  7 
 7кН
2
16  12
при z1  1м M X1  7 
 15кН
2
Исследуем параболу на экстремум: берем производную, приравниваем к
нулю:
dM X1
 qz1  0 .
dz1
M X1  7 
Тогда z1  0 (граница участка), при котором
16  0 2
 7кН .
2
Полученное значение z1 лежит в пределах рассматриваемого участка,
поэтому график параболы проводим по двум точкам на границах участка в
виде плавной кривой с экстремумом в z1  0 .
Уравнение поперечной силы
Q1 
dM X1
 qz1 - уравнение прямой.
dz1
при z1  0 Q1  16  0  0кН
при z1  1м Q1  16 1  16кН
Участок II. Справа 0,5L  z 2  L или 1м  z2  2 м .
Уравнение изгибающего момента
M X2  M  R B z 2  7  4z 2 - уравнение прямой. Ее значения на границах участка:
при z 2  1м M X2  7  4 1  11кН
при z 2  2 м M X2  7  4  2  15кН
Уравнение поперечной силы
Q2 
dM X2
 RB  4кН - уравнение const.
dz 2
при z 2  1м Q1  4кН
при z 2  2 м Q1  4кН
Участок III. Справа 0  z3  0,5L или 0 м  z3  1м .
Уравнение изгибающего момента
M X3  R B z3  4z 3 - уравнение прямой. Ее значения на границах участка:
при z 3  0 м M X3  4  0  0кН
при z3  1м M X3  4  1  4кН
Уравнение поперечной силы
Q3 
dM X3
 RB  4кН - уравнение const.
dz 3
при z 3  0 м Q1  4кН
при z3  1м Q1  4кН
Рис 4.5
Из эпюр имеем:
Mx
max
 15кНм ; Q max  16кН .
Из условия прочности по нормальным напряжениям
Wx 
Mx
max

Mx
max
Wx
  изг имеем
15  10 3
 0,1  10  4 м 3  100см 3 ,
150  10 6
 изг
где  изг  150МПа – допускаемое напряжение на изгиб для стали Ст3.
По таблице сортамента двутавров ГОСТ 8239-89 находим ближайшее
большее значение момента сопротивления сечения: Wтабл  109см 3 , что
соответствует двутавру №16.
Задание 5
Деревянная балка (рисунок 5.1) прямоугольного поперечного сечения
нагружена вертикальной силой F1 в точке 1 и горизонтальной силой F2 в
точке 2 (обе силы перпендикулярны оси балки). Требуется определить
размеры поперечного сечения балки при допускаемых напряжениях на изгиб
[]изг = 8МПа.
Рис 5.1
F1  3кН , F2  7кН , l  1,3 м и
h
 1,4 .
b
Решение
Отдельно рассматриваем изгиб балки в вертикальной и горизонтальной
плоскостях .
Рис 5.2
Определяем реакции опор в вертикальной плоскости (рис 5.2).
 mA  F1  0,5l  YB l  0 откуда YB  0,5F1  0,5  3  1,5кН
 mB  F1  0,5l  YAl  0 откуда YA  0,5F1  0,5  3  1,5кН
Делаем проверку: Y  YA  YB  F1  0 .
Строим эпюру изгибающего момента в вертикальной плоскости Мх, которая
будет являться ломаной прямой без разрывов.
Участок I: 0  z1  0,5l или 0  z1  0,65 м M X  YA z1  1,5z1
при z1  0 M X  0
при z1  0,65 м
M X  1,5  0,65  0,975кНм
Участок II: 0  z2  0,5l или 0  z 2  0,65м M X  YB z 2  1,5z2
при z 2  0 M X  0
при z 2  0,65м
M X  1,5  0,65  0,975кНм
Рис 5.3
Определяем реакции опор в горизонтальной плоскости, рассматривая вид
балки сверху (рис 5.3):
 mA  F2  0,7l  X B l  0 откуда X B  0,7F2  0,7  7  4,9Н
 mB  F2  0,3l  X Al  0 откуда X A  0,3F2  0,3  7  2,1кН
Делаем проверку:  X  X A  X B  F2  0 .
Строим эпюру изгибающего момента в вертикальной плоскости Мy, которая
будет являться ломаной прямой без разрывов.
M y   X A z1  2,1z1
Участок I: 0  z1  0,7l или 0  z1  0,91м
при z1  0 M y  0
M y  2,1  0,91  1,911кНм
при z1  0,91м
Участок II: 0  z2  0,3l или 0  z 2  0,39 м M y   X B z 2  4,9 z 2
при z 2  0 M y  0
M y  4,9  0,39  1,911кНм
при z 2  0,39 м
Для определения положения опасного сечения сравниваем эпюры моментов
Мх и Му и видим, что опасным сечением может быть либо сечение 1, либо
сечение 2. Находим напряжения в этих сечениях по формуле. Так как для
прямоугольного сечения Wx 
W
h
bh 2
hb 2
и Wy 
, то отношение x   1,4 .
Wy b
6
6
Тогда


 M x1  W x M y1   1 0,975  1,4  1,365  2,886

 W
Wy
Wx
x


 1
W
1 
3,2604

2 
M x2  x M y2  
0,585  1,4  1,911 
 W
W x 
Wy
Wx
x

1 
1
Wx
Сравнив напряжения в точках 1 и 2, приходим к выводу, что опасным
сечением является сечение 2.
Из расчета на прочность по опасному сечению определяем его размеры. В
условие прочности выражение момента сопротивления Wx подставляем с
h
bh 2 1,96b 3
учетом соотношения  1,4 : Wx 
, тогда

b
6
6
3,2604 6  3,2604
 max   2 

  изг , откуда
Wx
1,96b 3
6  3,2604  10 3
 0,108 м  10,8см . Округляем b  11см
1,96  8  10 6
Тогда h  1,4b  15,4см .
b3
Задание 6
На вал (рисунок 6.1), вращающийся с угловой скоростью , через шкив 1,
имеющий диаметр D1 и угол наклона ветвей ремня к горизонту 1, подается
мощность Р кВт. Два других шкива 2 и 3 имеют одинаковый диаметр D2,
одинаковые углы наклона ветвей ремня к горизонту 2 и каждый из них
передает потребителям мощность 0,5Р. Определить диаметр d вала из
расчета на прочность по опасному сечению, приняв пониженное значение
допускаемых напряжений на изгиб изг=70МПа.
Рис 6.1
a  0,5 м , b  0,4 м , c  0,6 м , P  30кВт ,   40c 1 , D1  400 мм , D2  250 мм ,  1  0 0 ,
 2  60 0
Решение
Приводим усилия в ременной передаче к центру вала.
Крутящие моменты на шкивах M 
  40c 1
.
На
ведомых M 2  M 3 
ведущем
0,5P


P

, где угловая скорость вращения вала
шкиве
M1 
30  10 3
 750 Нм
40
;
на
15  10 3
 375Нм .
40
На расчетной схеме вала моменты на ведущем шкиве M1 и на ведомых
шкивах M 2 и M 3 направляются в противоположные стороны.
Усилия в ветвях ременной передачи определяем, используя приближенное
соотношение T  2t , где Т – усилие в ведущей ветви, t – усилие в ведомой
TD tD 2tD tD tD
2M




, откуда t 
.
2
2
2
2
2
D
2M 1 2  750
На ведущем шкиве t1 

 3750 Н  3,75кН , T1  2t1  2  3,75  7,5кН
D1
0,4
2  375
На ведомых: t 2  t 3 
 3000 Н  3кН , T2  T3  2t 2  2  3  6кН .
0,25
Усилия в ветвях заменяем равнодействующими F  T  t .
На ведущем шкиве F1  T1  t1  11,25кН ;
ветви, тогда M 
на ведомых F2  F3  T2  t 2  9кН ;
Раскладываем равнодействующие на вертикальную и горизонтальную
составляющие:
X 1  F1 cos 1  11,25 cos 0 0  11,25кН
Y1  F1 sin 1  11,25sin 0 0  0кН
X 2  F2 cos  2  9 cos 60 0  4,5кН
Y2  F2 sin  2  9sin6 0 0  7,8кН
В результате расчета определены усилия, которые передаются на вал через
шкивы (рисунок 6.2).
Рис 6.2
Рисуем расчетную схему вала (рисунок 6.3), на которой вал изображен его
осью; шкивы убраны, и места их расположения обозначены точками 1,2,3, в
которые с рисунка 6.2 переносим соответствующие усилия. Таким образом,
вал испытывает два плоских изгиба в вертикальной и горизонтальной
плоскостях и кручение. Рассматриваем отдельно эти простые виды
деформации. Последующие схемы и эпюры размещаем для наглядности
столбиком.
Расчетная схема вала
Рис 6.3
Изгиб в вертикальной плоскости. Расчетная схема включает только
вертикальные силы. Подшипники заменяем шарнирными опорами А и В.
Определяем вертикальные реакции в опорах:
 mA  Y2  a  YB a  b  c  Y2 1,5a  b  c  0 , отсюда YB  11,7кН
 mB  Ya  a  b  c  Y2 b  c  Y2  0,5a  0 , отсюда YA  3,9кН
Проверка: Y  YA  YB  Y2  Y2  0 .
Строим эпюру изгибающего момента в вертикальной плоскости Мх. Так как
на балке нет распределенной нагрузки и сосредоточенных изгибающих
моментов, то эпюра будет представлять ломаную линию без скачков. Для ее
построения достаточно знать значения момента Мх на границах участков:
M xA  0
M x 2  YA a  1,95кН
M x1  YA a  b  Y2 b  0,39кН
M xB  YA a  b  c   Y2 b  c   1,95кН
M x3  YA 1,5a  b  c   Y2 b  c  0,5a   YB  0,5a  0кН
Изгиб в горизонтальной плоскости. Расчетная схема содержит только
горизонтальные силы.
Определяем горизонтальные реакции в опорах:
m
m
A
B
  X 2  a  X 1 a  b  X B a  b  c  X 2 1,5a  b  c  0 , отсюда X B  13,5кН
  X a  a  b  c  X 2 b  c  X 1c  X 2  0,5a  0 , отсюда X A  6,75кН
Проверка:  X  X A  X B  X 1  X 2  X 2  0 .
Строим эпюру изгибающего момента в вертикальной плоскости Мх. Так как
на балке нет распределенной нагрузки и сосредоточенных изгибающих
моментов, то эпюра будет представлять ломаную линию без скачков. Для ее
построения достаточно знать значения момента Мх на границах участков:
M yA  0
M y 2  X A a  3,375кН
M y1  X A a  b   X 2 b  4,275кН
M yB  X A a  b  c   X 2 b  c   X 1c  1,125кН
M x3  X A 1,5a  b  c   X 2 b  c  0,5a   X 1 c  0,5a   X B  0,5a  0кН
Строим эпюру результирующего изгибающего момента Мизг , складывая
геометрически его проекции Мх и Му , то есть M изг  M x2  M y2 .
M изг  A  0 2  0 2  0кНм
M изг 2  1,95 2  3,375 2  3,9кНм
M изг 1  0,39 2  4,275 2  4,3кНм
M изг B   1,952   1,1252  2,25кНм
M изг 3  0 2  0 2  0кНм
Кручение вала. К валу прикладываем только крутящие моменты М1, М2, М3 ,
потерями в подшипниках пренебрегаем. Строим эпюру внутренних крутящих
моментов Тк . Значения моментов кручения Тк на участках постоянны:
TkI  0
T kII  M 2  375Нм
TkIII  M 2  M 1  375Нм
Определяем положение опасного сечения, пользуясь двумя последними
эпюрами изгибающего момента Мизг и Тк . Так как обе эпюры имеют
максимальные значения в одной и той же точке 1 , то именно сечение 1 и
будет наиболее опасным. Вычисляем для опасного сечения величину
расчетного момента по четвертой гипотезе прочности :
2
M PIY  M изг
 0,75Т к2  (4,3) 2  0,75(0,375) 2  4,3кНм.
Расчет вала на прочность проводим по условию прочности на изгиб с
кручением :
Mp
   изг .
W
Подставив в него формулу для момента сопротивления круглого сечения
W
d 3
d 3
, получим значение диаметра вала
32
32M P
  изг
3
32  4,3  10 3
 0,0855 м  85,5 мм .
3,14  70  10 6
Полученное значение округляем до ближайшего нормального размера
d = 85 мм.
Задание 7
На балку, сваренную из двух швеллеров (рисунок 7.1), с высоты h падает
груз массой m. Найти максимальное значение нормальных напряжений в
балке в момент удара.
Рис 7.1
L  2,3 м , m  45кг , h  0,2 м и швеллер №16.
Решение
1. Решаем вспомогательную статическую задачу.
Находим напряжения и деформации от действия статически приложенной
силы тяжести груза G  mg  45  10  450 H (рисунок 7.3).
Строим эпюру изгибающего момента M ст .
Определяем реакции в опорах. Составляем уравнения равновесия.
Запишем уравнения моментов относительно опор A и B.
m
m
A
 0,4L  G  RB L  0
B
 1,4L  G  RA L  0
Решая уравнения, получаем RA  1,4G  630Н RB  0,4G  180Н
Участок I. ( 0  z1  0,4L или 0  z1  0,92 )
M ст  Gz1  450z1
при z1  0 M ст  450  0  0Hм
при z1  0,92 M ст  450  0,92  414Hм
Участок II. ( 0  z 2  L или 0  z 2  2,3 )
M ст  RB z 2  180z 2
при z 2  0 M ст  180  0  0Hм
при z 2  2,3 M ст  180  2,3  414Hм
Рис 7.2
Максимальные напряжения в опасном сечении
 ст 
M ст
max
2W x

414
 2,22МПа
2  93,4  10 6
,
где Wx=93,4 см3 – момент сопротивления швеллера №16.
Величина статического прогиба в точке приложения силы
G  0,4 L  0,4 L  L 
450  0,4  1,4  2,33


 3,42  10  4 м
11
8
6 EI x
6  2  10  747  10
2
y ст
При статическом расположении к балке массы 45 кг напряжения и
деформации пренебрежительно малы.
2. Находим напряжения в балке при ударе.
Определим сначала напряжения в балке при ударе без учета массы самой
балки. Динамический коэффициент по формуле
kД  1 1
2h
2  0,2
 1 1
 35,21
y ст
3,42  10 4
,тогда напряжения при ударе
 дин   ст  k Д  2,22  35,21  78,17 МПа
не превышают допускаемые значения
для этой стали  из  150МПа . Рассчитывать балку с учетом массы не
обязательно.
Проведем расчет с учетом массы балки.
Масса балки
M Б  mБ  1,4L  28,4  1,4  2,3  91,45кг ,
где mБ  28,4кг – масса 1м двух швеллеров №16.
Коэффициент приведения массы балки к точке удара определяем по
формуле приложения Е:

8  c 3 (140  231c  99c 2 ) 8  0,4 3 (140  231  0,4  99  0,4 2 )

 0,13
420(1  c) 3 c 2
420(1  0,4) 3 0,4 2
,
где с = 0,4 для заданной схемы.
Приведенная масса по формуле
M прив    M Б  0,13  91,45  11,85кг
.
Значение динамического коэффициента по формуле
kД  1 1
 1 1
y ст
2h

 (1  М прив / m)
2  0,2
 31.
3,42  10  (1  11,85 / 45)
4


k
 2,22  31  68,82МПа
ст
Д
Тогда напряжения при ударе дин
допускаемого при изгибе изг = 150МПа.
ниже
Таким образом, учет собственной массы конструкции снизил
максимальные напряжения в балке.
Задание 8
На плоской раме, продольными элементами которой являются два
швеллера (рисунок 8.1), установлен механизм массой m, имеющий ротор с
частотой вращения n оборотов в минуту. Центробежная сила инерции,
возникающая при вращении ротора вследствие его неуравновешенности,
равна Fин. Определить основные характеристики цикла напряжений в
опасном сечении рамы при ее установившихся колебаниях в вертикальной
плоскости.
Рис 8.1
l  2,3 м , m  300кг , n  250
об
, Fин  4кН и швеллер №16
мин
Решение.
Решение
Определяем постоянную составляющую нагрузки (сила тяжести механизма):
G  10m  10  300  3000Н  3кН
Строим эпюру изгибающего момента M пост в балке от действия силы тяжести
механизма (рисунок 8.3).
Определяем реакции в опорах.
 mAппос  G  0,7l  YBппос  l  0 , откуда YBппос  2,1кН
 mBппос  G  0,3l  YAппос  l  0 , откуда YAппос  0,9кН
Поскольку нет ни сосредоточенных моментов, ни распределенной нагрузки,
то эпюра изгибающих моментов будет представлять ломаную линию без
разрывов. Поэтому необходимо определить значения момента в характерных
точках.
M xA  0кНм
M x1  1,45кНм
M xB  0кНм
Максимальное значение постоянных напряжений в балке
 пост 
Mx
max
2W x
1,45  10 3

 7,76МПа
2  93,4  10 6
где W x  93,4см 3 – момент сопротивления швеллера №16.
Величина прогиба балки в точке крепления механизма от его силы тяжести
G  0,7l  l  0,7l 
3000  1,61 0,69

 0,36  10 3 м  0,36 мм
11
8
3EI x l
3  2  10  747  10  2,3
2
y ст 
2
2
2
где I x  747см 4 – момент инерции швеллера №16.
Круговая частота собственных колебаний
g
9,81

 165с 1 .
3
yст
0,36  10
0 
Круговая частота вынужденных колебаний

т
30

  250
30
 26с 1 .
«Отстройка» от резонанса составляет
0   
165  26 

  100%  
  100%  84,2% ,
 165 
 0 
что соответствует существующим
нормам (2030%), и частотной регулировки динамическая система не
требует.
Коэффициент нарастания колебаний

1
 
1   
 0 
2

1
 26 
1 

 165 
2
 1,03 .
Строим эпюру изгибающего момента M ст от действия статически
приложенной центробежной силы инерции Fст  Fин (рис. 8.4).
Определяем реакции в опорах.
 mAппос  Fин  0,7l  YBии  l  0 , откуда YBии  2,8кН
 mBппос  Fин  0,3l  YAии  l  0 , откуда YAии  1,2кН
Поскольку нет ни сосредоточенных моментов, ни распределенной нагрузки,
то эпюра изгибающих моментов будет представлять ломаную линию без
разрывов. Поэтому необходимо определить значения момента в характерных
точках.
M xA  0кНм
M x1  1,93кНм
M xB  0кНм
Вычисляем значение напряжений от действия этой силы
 ст 
M ст
max
2W x

1930
 10,3МПа
2  93,4  10 6
Тогда напряжения чисто от вибрации будут достигать
 вын   ст  1,03  10,3  10,6МПа
Характеристики цикла напряжений:
среднее значение  m   пост  7,76МПа ;
амплитуда цикла  a   вын  10,6МПа ;
максимальное значение напряжений  max   m   a  18,36МПа ;
минимальное значение напряжений  min   m   a  2,84МПа ;
коэффициент асимметрии цикла r 
 min
 2,84

 0,15
 max
18,36