Урок4.Тема. Синус, косинус, тангенс угла. Основное

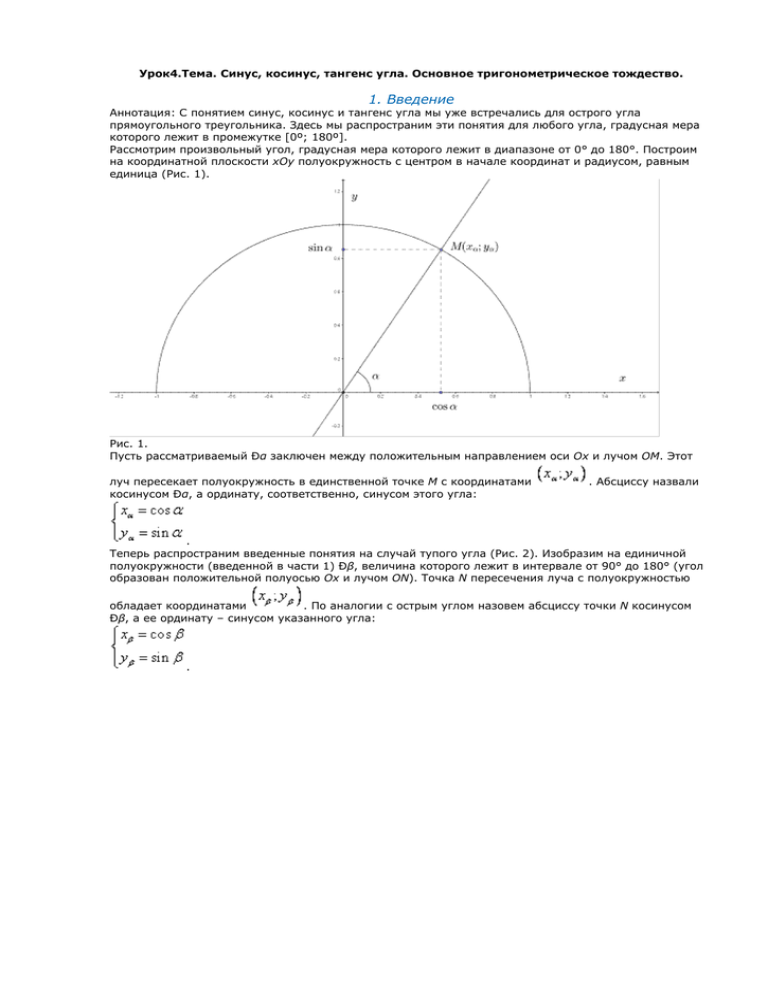
Урок4.Тема. Синус, косинус, тангенс угла. Основное тригонометрическое тождество.
1. Введение
Аннотация: С понятием синус, косинус и тангенс угла мы уже встречались для острого угла
прямоугольного треугольника. Здесь мы распространим эти понятия для любого угла, градусная мера
которого лежит в промежутке [0º; 180º].
Рассмотрим произвольный угол, градусная мера которого лежит в диапазоне от 0° до 180°. Построим
на координатной плоскости xOy полуокружность с центром в начале координат и радиусом, равным
единица (Рис. 1).
Рис. 1.
Пусть рассматриваемый Ðα заключен между положительным направлением оси Ох и лучом ОМ. Этот
луч пересекает полуокружность в единственной точке М с координатами
косинусом Ðα, а ординату, соответственно, синусом этого угла:
. Абсциссу назвали
.
Теперь распространим введенные понятия на случай тупого угла (Рис. 2). Изобразим на единичной
полуокружности (введенной в части 1) Ðβ, величина которого лежит в интервале от 90° до 180° (угол
образован положительной полуосью Ох и лучом ON). Точка N пересечения луча с полуокружностью
обладает координатами
. По аналогии с острым углом назовем абсциссу точки N косинусом
Ðβ, а ее ординату – синусом указанного угла:
.
Рис. 2.
Теперь введем строгие определения синуса и косинуса произвольного угла, градусная мера которого
лежит в интервале от 0° до 180° (Рис. 3).
Синусом Ðα называется ордината точки пересечения луча, образующего с положительным
направлением оси Ох Ðα с единичной полуокружностью, центр которой расположен в начале
координат.
Косинусом Ðα называется абсцисса точки пересечения луча, образующего с положительным
направлением оси Ох Ðα с единичной полуокружностью, центр которой расположен в начале
координат.
Рис. 3.
Из Рис. 3 видно, что косинус угла может меняться в пределах от – 1 до 1, а синус угла – от 0 до 1.
Теперь рассмотрим конкретные примеры, которые, с одной стороны, решаются исходя из определения
синуса и косинуса и, с другой стороны, разъясняют нам эти
определения
Рис. 4.
Первый пример для угла в 0º, т. е. для координат точки A (1; 0).
1. А (1; 0) = А (
)
,
Второй пример для угла в 90º. Ð90º соответствующая точка С (0; 1) или
С(
).
2. С (0; 1) = С(
). Значит,
,
.
И наконец, для третьего угла, угла в 180º (ему соответствует точка В (–1; 0)
или
В(
).
3. В (–1;0) = В(
).
Теперь понятно, что
,
.
Итак, мы знаем, что такое синус угла, что такое косинус угла, умеем вычислять значения синуса и
косинуса. Теперь с помощью этих понятий определим тангенс.
Тангенсом угла α (α ≠ 90º) называется отношение синуса этого угла к его косинусу,
т. е.
.
При α = 90º
не определен, поскольку косинус 90º = 0, знаменатель равен 0, что невозможно.
, потому что синус здесь равен 0, а косинус не равен 0.
Теперь другое важное определение.
Котангенсом угла α (α ≠ 90º, α ≠ 180º) называется отношение косинуса этого угла к его синусу,
т. е.
.
Пример:
.
А почему здесь (α ≠ 0, α ≠ 180º)?
Потому что при этих углах синус, стоящий в знаменателе, равен 0, что недопустимо.
Отметим также формулу – связь котангенса и тангенса:
.
Каким образом найти синус и косинус какого-либо угла?
Обратимся к рисунку.
Мы уже занимались этим. Вот есть угол. Первое, что мы находили, – это точка М (Рис. 3). Затем
находили координаты точки, т. е. проектировали точку ее на оси координат и соответствующим
образом находили синус и косинус данного угла.
Теперь все наши действия облечем в такое правило. Чтобы найти sin α и cos α, надо, во-первых,
провести луч ОМ, спроектировать соответствующую точку Мполуокружности на оси координат. И тогда
абсцисса точки М даст косинус угла, а ордината точки даст синус угла. Подчеркнем, что угол здесь
лежит в пределах от 0 до 180º. Правило сформулировано.
Теперь рассмотрим основное тригонометрическое тождество. Основное тригонометрическое тождество
вытекает из уравнения единичной окружности, вспомним его: этох2 + у2 = 1 – уравнение единичной
окружности с центром в начале координат.
Но в рамках нашей нынешней темы х – это косинус угла, у – это синус угла, и в результате получаем
основное тригонометрическое тождество:
Ранее мы знали это тождество для ÐαÎ (0º; 90º).
1. Теперь рассмотрим формулы приведения:
. Подчеркнем, что здесь α Î [0º; 180º].
1.
при 0º £ α £ 90º. Это первая группа.
2. Вторая группа формул:
Строгое доказательство этих формул предстоит нам в курсе алгебры. А сейчас просто почувствуем,
почему они справедливы. Рассмотрим вторую группу формул с помощью Рис. 5.
На рисунке показан угол α, соответствующая ему точка М, косинус и синус показанного угла.
Из рисунка видно, что углу (180º – α) соответствует точка N единичной полуокружности. Для этого
угла показаны
. Заметим, что прямоугольные треугольники ∆ОММ1 =
∆ОNN1 по гипотенузе и острому углу. Следовательно, все соответственные элементы треугольников
равны друг другу. В частности, ММ1 = NN1, а это есть не что иное как синус одного и второго угла.
Значит, синусы равны
.
Вторые катеты тоже равны: ОМ1 = ОN1, значит,
. Таким образом, мы
рассмотрели формулы приведения.
Итак, мы определили понятие синуса, косинуса, тангенса, котангенса угла для любого угла из
промежутка [0º; 180º]. Вывели основное тригонометрическое тождество. Далее синус и косинус будут
использованы для определения координат точки.
Рекомендованные ссылки на интернет-ресурсы
1. Твой личный наставник (Источник).
Рекомендованное домашнее задание
Выучить конспект.Сделать табличку-памятку.