2. нормальное распределение

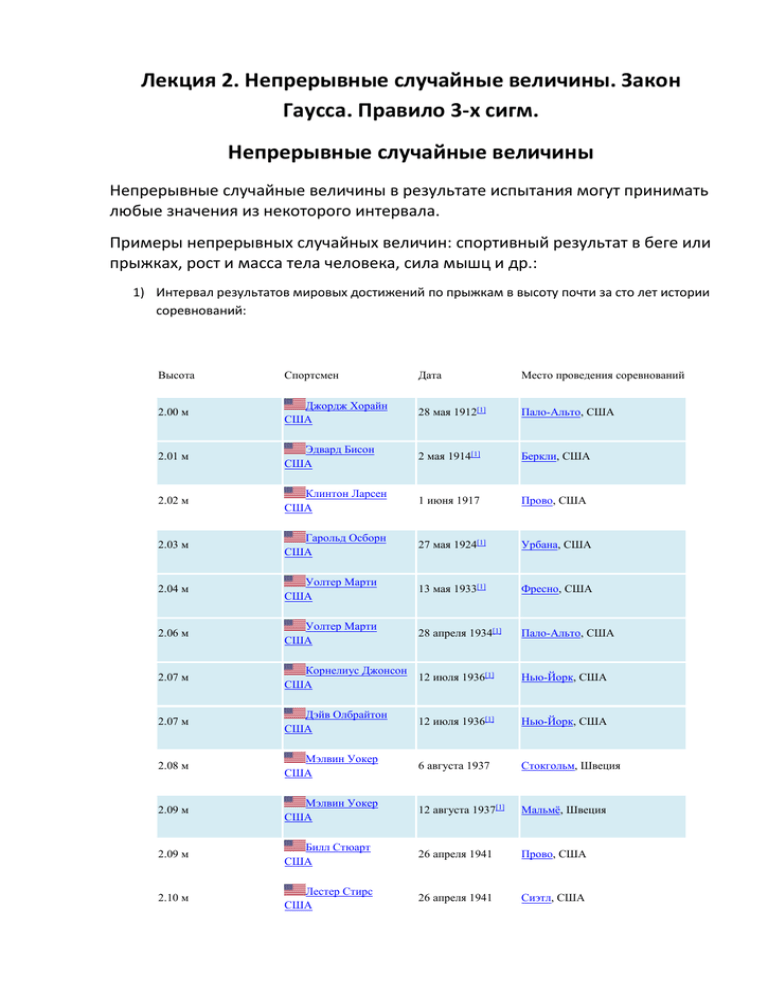
Лекция 2. Непрерывные случайные величины. Закон
Гаусса. Правило 3-х сигм.
Непрерывные случайные величины
Непрерывные случайные величины в результате испытания могут принимать
любые значения из некоторого интервала.
Примеры непрерывных случайных величин: спортивный результат в беге или
прыжках, рост и масса тела человека, сила мышц и др.:
1) Интервал результатов мировых достижений по прыжкам в высоту почти за сто лет истории
соревнований:
Высота
Спортсмен
Дата
Место проведения соревнований
2.00 м
Джордж Хорайн
США
28 мая 1912[1]
Пало-Альто, США
2.01 м
Эдвард Бисон
США
2 мая 1914[1]
Беркли, США
2.02 м
Клинтон Ларсен
США
1 июня 1917
Прово, США
2.03 м
Гарольд Осборн
США
27 мая 1924[1]
Урбана, США
2.04 м
Уолтер Марти
США
13 мая 1933[1]
Фресно, США
2.06 м
Уолтер Марти
США
28 апреля 1934[1]
Пало-Альто, США
2.07 м
Корнелиус Джонсон
12 июля 1936[1]
США
Нью-Йорк, США
2.07 м
Дэйв Олбрайтон
США
12 июля 1936[1]
Нью-Йорк, США
2.08 м
Мэлвин Уокер
США
6 августа 1937
Стокгольм, Швеция
2.09 м
Мэлвин Уокер
США
12 августа 1937[1]
Мальмё, Швеция
2.09 м
Билл Стюарт
США
26 апреля 1941
Прово, США
2.10 м
Лестер Стирс
США
26 апреля 1941
Сиэтл, США
2.105 м
Лестер Стирс
США
24 мая 1941
Лос-Анжелес, США
2.11 м
Лестер Стирс
США
17 июня 1941[1]
Лос-Анжелес, США
2.12 м
Уолтер Дэвис
США
27 июня 1953[1]
Дейтон, США
2.15 м
Чарльз Дюмас
США
29 июня 1956[1]
Лос-Анжелес, США
2.16 м
Юрий Степанов
СССР
13 июля 1957[1]
Ленинград, СССР
2.17 м
Джон Томас
США
30 апреля 1960[1]
Филадельфия, США
2.17 м
Джон Томас
США
21 мая 1960[1]
Кембридж, США
2.18 м
Джон Томас
США
24 июня 1960[1]
Бейкерсфилд, США
2.195 м
Джон Томас
США
1 июля 1960
Пало-Альто, США
2.22 м
Джон Томас
США
1 июля 1960[1]
Пало-Альто, США
2.23 м
Валерий Брумель
СССР
18 июня 1961[1]
Москва, СССР
2.24 м
Валерий Брумель
СССР
16 июля 1961[1]
Москва, СССР
2.25 м
Валерий Брумель
СССР
31 августа 1961[1]
София, Болгария
2.26 м
Валерий Брумель
СССР
22 июля 1962[1]
Пало-Альто, США
2.27 м
Валерий Брумель
СССР
29 September 1962[1] Москва, СССР
2.28 м
Валерий Брумель
СССР
21 июля 1963[1]
Москва, СССР
2.29 м
Ни Чичин
КНР
8 ноября 1970
Чанша, КНР
2.29 м
Пэт Мэтсдорф
США
3 июля 1971[1]
Беркли, США
2.30 м
Дуайт Стоунс
США
11 июля 1973[1]
Мюнхен, ФРГ
2.31 м
Дуайт Стоунс
США
5 июня 1976[1]
Филадельфия, США
2.32 м
Дуайт Стоунс
США
4 августа 1976[1]
Филадельфия, США
2.33 м
Владимир Ященко
СССР
2 июня 1977[1]
Ричмонд, США
2.34 м
Владимир Ященко
СССР
16 июня 1978[1]
Тбилиси, СССР
2.35 м
Яцек Вшола
ПНР
25 мая 1980[1]
Эберштадт, ФРГ
2.35 м
Дитмар Мёгенбург
ФРГ
26 мая 1980[1]
Рейлинген, ФРГ
1 августа 1980[1]
Москва, СССР
Пекин, КНР
2.36 m
Герд Вессиг
ГДР
2.37 м
Чжу Цзяньхуа
КНР
11 июня 1983[1]
2.38 м
Чжу Цзяньхуа
КНР
22 сентября 1983[1] Шанхай, КНР
2.39 м
Чжу Цзяньхуа
КНР
10 июня 1984[1]
2.40 м
Рудольф Поварницын
11 августа 1985[1]
СССР
Донецк, СССР
2.41 м
Игорь Паклин
СССР
4 сентября 1985[1]
Кобе, Япония
2.42 м
Патрик Шёберг
Швеция
30 июня 1987[1]
Стокгольм, Швеция
2.43 м
Хавьер Сотомайор
Куба
8 сентября 1988[1]
Саламанка, Испания
2.44 м
Хавьер Сотомайор
Куба
29 июля 1989[1]
Сан-Хуан, Пуэрто-Рико
2.45 м
Хавьер Сотомайор
Куба
27 июля 1993[1]
Саламанка, Испания
Эберштадт, ФРГ
Валерий Николаевич Брумель — легендарный советский легкоатлет, заслуженный мастер
спорта СССР. Чаще Брумеля никто из мужчин не устанавливал мировых рекордов в прыжках в
высоту.
2) Интервал значений роста современных людей (март 2010):
Сотни фотографов снимали эту необычную встречу: самый большой человек в мире турок
Султан Косен (Sultan Kosen) пожал руку самому маленькому человеку планеты - китайцу Хэ
Пинпину. Рост Султана - 2 метра 46,5 сантиметров. Малыш Пинпин со своими 73-мя
сантиметрами едва-едва доходит гиганту до колена.
Так как число возможных значений непрерывной случайной величины
бесконечно велико и чаще всего нет оснований предположить, что одни
значения появляются существенно чаще других, то вероятность принятия
непрерывной случайной величиной каждого отдельного значения
оказывается равной нулю. По этой причине нельзя описать распределение
непрерывной случайной величины в виде вероятностей ее отдельных
значений, как в случае дискретных случайных величин.
Функция плотности распределения вероятности (ПВР)
Вероятность dP того, что непрерывная случайная величина примет
значение, принадлежащее интервалу ( x , x+dx) равна
𝑑𝑃 = 𝑓(𝑥)𝑑𝑥,
где f(x) – функция плотности распределения вероятности (является
вероятностью, приходящейся на единицу длины, рассматриваемого участка).
Вероятность того, что случайная величина принимает значения из интервала
𝒙
[x1,x2] рассчитывается по формуле: 𝑷(𝒙) = ∫𝒙 𝟐 𝒇(𝒙)𝒅𝒙
𝟏
Функция f(x) показывает следующую важнейшую информацию: вероятность
числовой величине х принять значение больше числа x1 и меньше числа x2
равна площади под кривой f(x) на отрезке [x1, x2]. Разумеется, это касается
любых x1 и x2, близких между собой или далеких, расположенных в любом
месте прямой х.
Из наиболее известных видов распределения непрерывных случайных
величин наиболее часто используют нормальное распределение,
описываемое законом Гаусса. Впервые нормальный закон был обнаружен в
Х1Х веке в применении к теории ошибок измерения Лапласом и Гаусcом.
Гаусс (Gauss) Карл Фридрих (30.4.1777, Брауншвейг, — 23.2.1855, Гёттинген), немецкий математик,
внёсший фундаментальный вклад также в астрономию и геодезию
Пьер-Симо́н Лапла́с (фр. Pierre-Simon Laplace; 23 марта 1749 — 5 марта 1827) — выдающийся
французский математик, физик и астроном; известен работами в области небесной механики,
дифференциальных уравнений, один из создателей теории вероятностей.
Сейчас, после доказанной А. М. Ляпуповым центральной предельной
теоремы, стало уже ясным, почему этот нормальный закон широко
распространен в технике, биологии, социологии, психологии и многих других
сферах человеческих знаний.
Ляпунов Александр Михайлович [25.5(6.6). 1857, Ярославль, — 3.11.1918, Одесса], русский математик
и механик, академик Петербургской АН.
Центральная предельная теорема утверждает, что всегда, когда
случайная величина образуется в результате сложения большого числа
независимых случайных величин с конечными дисперсиями, закон
распределения этой случайной величины оказывается практически
нормальным законом. А поскольку случайные величины всегда
порождаются бесконечным количеством причин, и чаще всего ни одна из
них не имеет дисперсии, сравнимой с дисперсией самой случайной
величины, то большинство встречающихся в практике случайных величин
подчинено нормальному закону распределения.
Например, рост человека, на который оказывают влияние очень много факторов, среди
которых в массе нет доминирующих по своему влиянию.
Нормальное распределение, также называемое гауссовским
распределением или распределением Гаусса — распределение
вероятностей, которое задается функцией плотности распределения:
где параметр μ — среднее значение (математическое ожидание) случайной
величины и указывает координату максимума кривой плотности
распределения, а σ² — дисперсия.
f(x)
x
μ
Плотность распределения вероятностей нормального закона, причем,
1,2 - графики с одним средним μ и разными стандартными отклонениями σ , причем,
σ 1 < σ2.
График плотности вероятности нормального закона распределения
симметричен относительно вертикальной прямой x max = μ. Причем, в точке
x max = μ функция имеет максимум, равный 𝒚𝒎𝒂𝒙 =
𝟏
𝝈√𝟐𝝅
.
Кроме того, площадь под всей кривой f(x) равна 1, т.е. вероятность для х
попасть на прямую равна 1, и это событие достоверное. Это свойство еще
называется условием нормировки.
+∞
𝑷(𝒙) = ∫ 𝒇(𝒙)𝒅𝒙 = 1
−∞
Меняя μ, можно совершать параллельный перенос кривой f(x) вдоль оси х.
Видно также, что наиболее вероятно появление числа х в эксперименте
вблизи μ: площадь под f(x)на любом отрезке, содержащем μ, самая большая.
Число σ есть среднее отклонение числового показателя х от числа μ, чем
меньше σ, тем “круче” становится “холм” f(x) и тем меньше вероятность для х
сильно отличаться от µ.
Наоборот, при больших σ “холм” f(x) растекается по “равнине” и с почти
равной вероятностью х может появиться как вблизи μ, так и сколь угодно
далеко от μ .
Правило « трёх сигм»
Вероятность того, что случайная величина отклонится от своего
математического ожидание на величину, большую, чем утроенное
среднее квадратичное отклонение, практически равна нулю.
Расчеты показали, что вероятность попадания нормально распределенной
случайной величины в интервалы значений следующие:
I.
II.
III.
Р (µ-σ < x< µ+σ )= 68,26%
P (µ-2σ < x< µ+2σ )= 95,44%
Р (µ-3σ < x< µ+3σ ) = 99,72%
На практике считается, что если для какой – либо случайной величины
выполняется правило трех сигм, то эта случайная величина имеет
нормальное распределение.
Распределение Гаусса − одно из самых распространенных в физике. Такому
распределению подчиняются ошибки измерения физических величин,
результаты стрельбы по мишени, распределение проекций скоростей
молекул газа (распределение Максвелла), вероятность малых флуктуаций и
многое другое.
Задания:
1. На основании примеров графиков функции нормального
распределения запишите уравнения для соответствующих функций
ПРВ:
2. Предположим, что результаты стрельбы распределены по
нормальному закону. Смоделируйте вид кривых распределения
плотности вероятности результатов стрельбы снайпера и дилетанта: