Zadacha_3-Tonkostennaya_obolochka

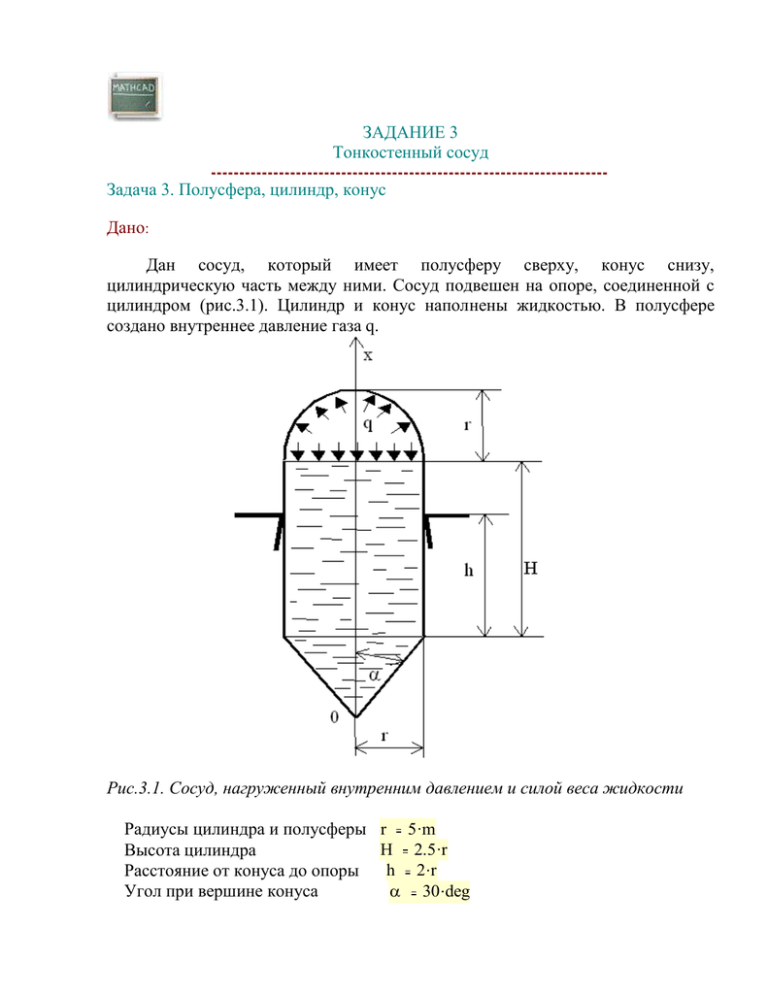
ЗАДАНИЕ 3
Тонкостенный сосуд
Задача 3. Полусфера, цилиндр, конус
Дано:
Дан сосуд, который имеет полусферу сверху, конус снизу,
цилиндрическую часть между ними. Сосуд подвешен на опоре, соединенной с
цилиндром (рис.3.1). Цилиндр и конус наполнены жидкостью. В полусфере
создано внутреннее давление газа q.
Рис.3.1. Сосуд, нагруженный внутренним давлением и силой веса жидкости
Радиусы цилиндра и полусферы r
H
Высота цилиндра
h
Расстояние от конуса до опоры
Угол при вершине конуса

5 m
2.5 r
2 r
30 deg
q
Внутреннее давление газа в полусфере
3
Удельный вес жидкости
 0.01 N cm
 lim 220 MPa
Допускаемое напряжение
0.5 MPa
Требуется:
1. Построить эпюры тангенциальных и меридиональных напряжений
 t и  m.
2. Рассчитать необходимую толщину стенки 
Решение.
1. Разместим начало координатной оси х в вершине конуса и на- правим
ось х вверх. Рассмотрим последовательно все четыре силовые участка.
1.1. Конус
Высота конуса
z
0 x z
r
tan (  )
На уровне х внутреннее давление равно сумме давления газа и
гидростатического давления жидкости.
p1 ( x)
q
 ( H
z
x)
Радиус кривизны на этом же уровне 1 ( x) равен
xtan (  )
1 ( x)
cos (  )
На основании уравнения Лапласа тангенциальное напряжение как функция
координаты х и толщины сосуда  равно
1 t ( x   )
p1 ( x) 1 ( x)

Уравнение равновесия отсеченной нижней части конуса (Рис.3.2.)
r1 x( x)
xtan (  )
Меридиональное напряжение уравновешивает давление газа и вес жидкости в
нижней части конуса и в цилиндре над этой частью конуса.
2
1 m ( x   ) 2  r1 x( x)  cos (  )  q r1 x( x) 
    ( H
2
z
x) r1 x( x)
2
2
 r1 x( x) x
3
Рис.3.2. Равновесие нижней части конуса
Из этого уравнения находим зависимость меридионального напряжения от
координаты и толщины стенки
1 m ( x   )
q r1 x( x)
1 m ( 1 m  5 mm )  46.996 MPa
  (H
z
x) r1 x( x)
r1 x( x) x
3
2  cos (  )
Можно рассуждать и иначе. Меридиональное напряжение
уравновешивает давление газа и гидростатическое давление на уровне x и вес
жидкости в нижней части конуса.
11 m ( x   ) 2  r1 x( x)  cos (  )  p1 ( x) r1 x( x)
11 m ( x   )
p1 ( x) r1 x( x)
 r1 x( x) x
2  cos (  )
3
3
2
2
  r1 x( x) x
3
1.2. Цилиндрическая часть ниже опоры, z x z
h
Давление на этом уровне равно
p2 ( x) q  ( H z x)
Радиус кривизны постоянен:
2 ( x) r
На основании уравнения Лапласа имеем для тангенциального напряжения:
p2 ( x) 2 ( x)
2 t ( x   )

Уравнение равновесия отсеченной нижней части цилиндра с конусом
(рис.3.3):
Рис.3.3. Равновесие нижней части цилиндра и конуса
r2 x( x) r
Меридиональное напряжение уравновешивает давление газа и весь вес
жидкости в конусе и в цилиндре над конусом.
2
2
2  r z









2 m ( x   ) 2  r   q r
 Hr
3
Из этого уравнения находим зависимость меридионального напряжения
от координаты и толщины стенки для второго участка:
4
q r
2 m ( x   )
r z
3
  H r
2 
1.3. Цилиндрическая часть выше опоры, z h x z H
Тангенциальное напряжение равно тангенциальному напряжению на втором
участке
3 t ( x   ) 2 t ( x   )
Рис.3.5. Равновесие верхней части цилиндра и полусферы
Рис.3.4. Равновесие нижней части цилиндра c опорой и конуса
Меридиональное напряжение проще всего найти из условия равновесия
верхней части.
Уравнение равновесия отсеченной верхней части (рис.3.5.)
2
3 m ( x   ) 2  r   q r
5
Из этого уравнения получаем выражение для меридионального напряжения на
третьем участке
q r
3 m ( x   )
2 
Меридиональное напряжение можно найти и из условия равновесия
нижней части сосуда. В этом случае надо учесть реакцию опоры Q (рис. 3.4.),
равную весу жидкости в сосуде
2
r
z 2
Q   
r H
3
Уравнение равновесия нижней части
33 m
( x   ) 2  r 
q r
2
Q  q r
  H r
33 m ( x   )
2
 r z
3
2
   H r
r z
3
Q
 r
2 
1.4. Сферическая часть, z
H x z
H
r
На основании уравнения Лапласа
q r
4 t ( x   )
2 
4 m ( x   )
4 t ( x   )
Запишем зависимость тангенциальных напряжений от координаты х для
всего сосуда:
 t( x  )
1 t ( x   ) if 0 x z
2 t ( x   ) if z x z
h
3 t ( x   ) if z
h x z
H
4 t ( x   ) if z
H x z
H
6
r
Зависимость меридиональных напряжений от координаты х для всего сосуда
имеет вид:
 m( x  )
1 m ( x   ) if 0 x z
2 m ( x   ) if z x z
h
3 m ( x   ) if z
h x z
H
4 m ( x   ) if z
H x z
H
r
Теперь построим эпюры тангенциальных и меридиональных напряжений
(рис.3.6). Зададим ранжированную переменную x:
x
0 mm  20 mm  z
H
r
30
x
m
25
20
x
m
15
x
10
m
5
0
0
50
100
150
200
 t ( x  30 mm)  m( x  30 mm)  lim


MPa
MPa
MPa
250
Рис.3.6. Эпюры тангенциальных и меридиональных напряжений
2. Определение допустимой толщины стенки.
Поскольку максимальное напряжение, как это следует из приведенных
эпюр, - это тангенциальное напряжение на конце первого силового участка, то
для обеспечения прочности оно не должно превышать предельного.

10 mm
7
Given
1 t ( z   )  lim
 Find (  )
(Критерий прочности)
  16.402 mm
Таким образом, нужная толщина стенки (с округлением в большую
сторону) равна
 
ceil
mm  17 mm
mm
8