Модифицируемый метод Эйлера

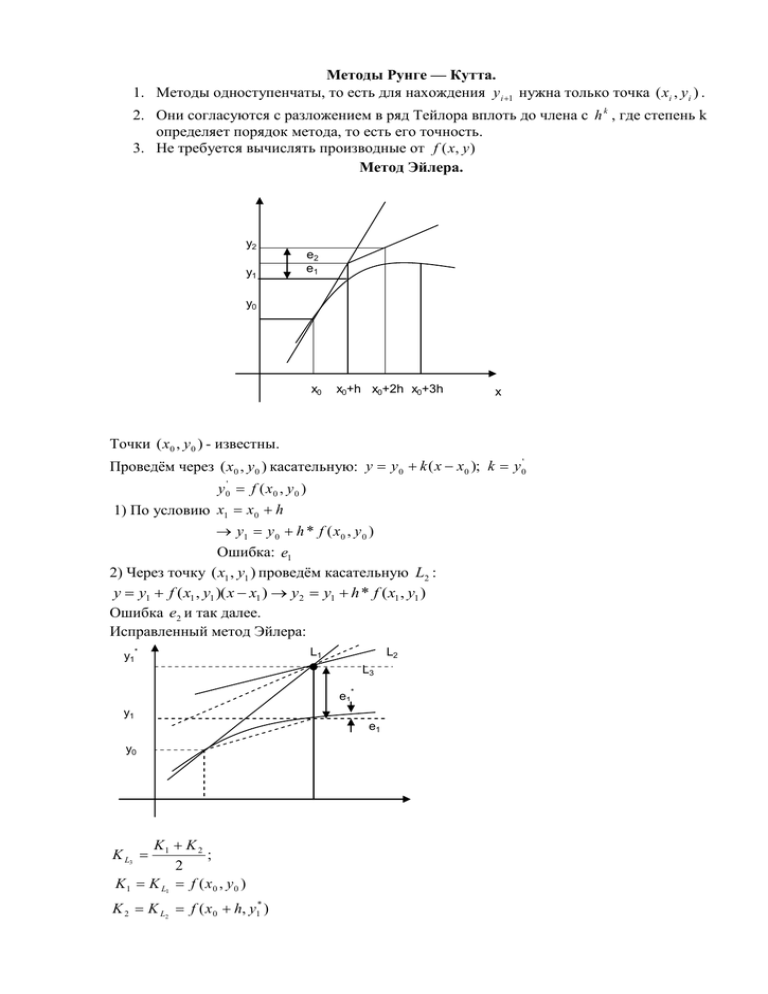
Методы Рунге — Кутта.
1. Методы одноступенчаты, то есть для нахождения y i 1 нужна только точка ( xi , yi ) .
2. Они согласуются с разложением в ряд Тейлора вплоть до члена с h k , где степень k
определяет порядок метода, то есть его точность.
3. Не требуется вычислять производные от f ( x, y )
Метод Эйлера.
y2
y1
e2
e1
y0
x0
x0+h x0+2h x0+3h
x
Точки ( x0 , y0 ) - известны.
Проведём через ( x0 , y0 ) касательную: y  y 0  k ( x  x0 ); k  y 0'
y 0'  f ( x0 , y 0 )
1) По условию x1  x0  h
 y1  y 0  h * f ( x0 , y 0 )
Ошибка: e1
2) Через точку ( x1 , y1 ) проведём касательную L2 :
y  y1  f ( x1 , y1 )( x  x1 )  y2  y1  h * f ( x1 , y1 )
Ошибка e2 и так далее.
Исправленный метод Эйлера:
y1*
L1
L2
L3
e1*
y1
y0
K1  K 2
;
2
K 1  K L1  f ( x0 , y 0 )
K L3 
K 2  K L2  f ( x0  h, y1* )
e1
где y1*  y 0  h * f ( x0 , y 0 ) , то есть K 2  f ( x0  h, y0  h * f ( x0 , y0 ))
K L3  K L4 
f ( x0 , y 0 )  f ( x0  h, y 0  h * f ( x0 , y 0 ))
2
1
h [ f ( x0 , y 0 )  f ( x0  h, y 0  h * f ( x0 , y 0 ))]
2
1
 y m  h [ f ( x m , y m )  f ( x m  h, y m  h * f ( x m , y m ))]
2
y1  y 0 
y m 1
f ( x, y)  f ( xi , yi )  ( x  xi ) f x'  ( y  yi ) f y'
f ( x0  h, y0  h * f ( x0 , y0 ))  f ( x0 , y0 )  h f x'  h * f ( x0 , y0 ) f y'
Модифицированный метод Эйлера.
h
y1*  y 0  f ( x0 , y 0 )
2
h
h
h
K L3  K L3  f ( x0  , y1* )  f ( x 0  , y 0  f ( x0 , y 0 ))
2
2
2
h
h
y1  y 0  h * f ( x0  , y 0  f ( x0 , y 0 ))
2
2
h
h
y m 1  y m  h f ( x m  , y m  f ( x m , y m ))
2
2
L1
y1*
L2
L3//L2
y1
y0
x0
Метод Эйлера.
y2
y1
e2
e1
y0
x0
x0+h x0+2h x0+3h
x
Точка ( x0 , y0 ) - известна.
Проведём через ( x0 , y0 ) касательную y  y 0  k ( x  x0 ) , где k  y 0' .
Так как по условию: y 0'  f ( x0 , y 0 )
x1  x0  h
Откуда y1  y0  h * f ( x0 , y0 ) .
Ошибка равна e1 , затем e2 , так как y2  y1  h * f ( x1 , y1 )
Исправленный метод Эйлера
L2
y1*
L1
L4
y1
L3
y0
x0
x0 +h
Через ( x0 , y0 ) проведём L` : K1  K L1  f ( x0 , y 0 )
Через ( x1 , y1* ) проведём L2 : K 2  K L2  f ( x0  h, y1* )
K1  k 2
2
f ( x0 , y0 )  f ( x0  h, y0  h * f ( x0 , y0 ))
K3  K 4 
2
Затем K 3  K L3 
1
h [ f ( x0 , y 0 )  f ( x0  h, y 0  h * f ( x0 , y 0 ))]
2
1
 y m  h [ f ( x m , y m )  f ( x m  h, y m  h * f ( x m , y m ))]
2
y1  y 0 
y m 1
Метод Рунге – Кутта 4-го порядка.
h
y m 1  y m  ( K 1  2 K 2  2 K 3  K 4 )
6
K1  f ( xm , y m )
h
h
K 2  f ( xm  , y m  K1 * )
2
2
h
h
K 3  f ( xm  , y m  K 2 * )
2
2
K 4  f ( x m  h, y m  K 3 * h)
Программы:
h
y m 1  y m  [ f ( x m , y m )  f ( x m  h, y m  h f ( x m , y m ))]
2
Sub Euler ()
Dim x As Single ' начальное значение
Dim x1 As Single ' конечное значение
Dim N As Integer ' число шагов
Dim Y As Single ' начальное значение функции
Dim H As Single ' шаг интегрирования
H = (x1 – x) / N: y1 = y
For i = 1 to N
Call funk (x, f): f1 = f
x = x + h: y = y + f * h: call funk (x, f)
y = y1 + h * (f1 + f) / 2: y1 = y
next i
sub funk (x, f)
f = - exp (- x)
end sub
y’ =  e  x ; y(0)  1; x  2; n  20
y = e 2  0,13533528 - точное
y (2) = 0,13461485 – метод Эйлера
Модифицированный метод Эйлера.
h
h
y m 1  y m  h[ f ( x m  , y m  f ( x m , y m ))]
2
2
h = (x1 - x) / N/2: y1 = y
for i = 1 to n
call funk (x, f )
x = x + h: y = y + f * h: call funk (x, f)
y1
Модифицируемый метод Эйлера
h
h
ym+n = ym + h[f(xm+ , ym + f(xm, ym)]
2
2
h = (x1 – x)/N/2 : y1 = y
for i = 1 to n
call funk(x, f)
x = x + h: y = y + f * h: call funk(x, f)
y1 = y1 + f * 2 * h : x = x + h : y = y1
next i
y(2) = ,135695455
Усовершенствованный метод последовательный приближений
y=f(x)
f(a)
f(xn-1)
45°
Q
f(xn)
(λ-1)∆x
∆x
λ∆x
xn
xn+1
a
f(xn-1) = xn; f(xn) = xn+1
∆x = xn-1 – xn = f(xn) - xn
xn+1 = xn + ∆x, лучше взять xn+1 = xn + λ *∆x, λ>1
(  1)x   1
1

 1
tg  =
x


f (a)  f ( xn)
 f ' ( ) , где xn    a
tg  =
a  xn
1

1  f ' ( )
 —известно, но можно
принять
f'(
f ( xn)  f ( xn  1) f ( xn)  xn
) 

xn  xn  1
xn  xn  1
f'(  ) = 1 
1
 
Геометрический процесс
отыскания следующего
приближения xn-1 сводится к
тому, что проводится хорда
через точки (xn, f(xn)) и (xn-1,
f(xn-1)) и определяется точка ее пересечения с прямой y = x.
Сходимость:
1) 0<f'(x)<1  1<  < 
поправки ∆x малы, но 1<  <   увеличит их и сходимость улучшиться
2) -1<f'(x)<0

1
 1
2
1
   1 их
2
уменьшит и метод сходится
быстрее: поправки уменьшаются
1
на коэффициент между
и 1.
2
поправки велики, а
Расходится:
3) f'(x)>1


1
0
1  f ' ( )
Так как   0 , то в
усовершенствованном методе
знаки поправок изменяются
нужным образом.
axn
4) f'(x)<-1

xn+1
0<  
1
— расходится, так как поправки велики
2
1
и процесс расходится.
2
Описанная модификация метода итераций принадлежит Векштейну (1958 г)
Каждая поправка умножается на коэффициент между 0 и
Пусть xn   1  a и   xn
1

1  f ' ( xn )
Метод Ньютона – Рафсона
f ( xn )  xn
f ( xn )  xn f ' ( xn )

1  f ' ( xn )
1  f ' ( xn )
f ( x)  x f ' ( x)
 g ( xn ), где g ( x) 
1  f ' ( x)
xn1  xn   * x  xn   ( f ( xn )  xn )  xn 
(1) xn1 
f ( xn )  xn f ' ( xn )
или xn1
1  f ' ( xn )
Если g ' ( x)  1 , то метод сходится:
 f ' ( x)  f ' ( x)  xf ' ' ( x)1  f ' ( x)   f ( x)  xf ' ( x)( f ' ' ( x)) 
1  f ' ( x)2
 xf ' ' ( x)  xf ' ' ( x) f ' ( x)  f ( x) f ' ' ( x)  xf ' ( x) f ' ' ( x) f ' ' ( x) f ( x)  x 


1  f ' ( x)2
1  f ' ( x)2
g ' ( x) 
Так как f (x) = x, (F (x) = 0 = x – f (x)), то для x, близких к «a», (f (x) - x) – мало. Поэтому (1)
сходится, если:
1) x 0 выбрано близко к решению x = f (x)
2) f ''(x) – не становится слишком большой.
3) f ' (x) не слишком близка к 1.
Это и есть знаменитый метод Ньютона – Рафсона.
f ( xn )  xn f ' ( x) xn  F ( xn )  xn ( x' n  F ' ( xn )) xn  F ( xn )  xn  xn F ' ( xn )
F ( xn )
xn1 


 xn 
1  f ' ( xn )
F ' ( xn )
F ' ( xn )
F ' ( xn )
F (x) = x – f (x) = 0
Или:
1) x 0 близко к корню F (x) = 0
2) F ' ' ( x) 0 - не слишком большая
3) F ' ( x0 ) - не близка к нулю
«3)» означает, что никакие два корня не находятся слишком близко один к другому.
Геометрическое толкование.
а)   xn , то есть  равен углу наклона касательной к y = f (x) в точке x  xn
y=f(x)
xn
б)
a
xn+2
xn+1
y=F(x)
a
xn+2
xn+1
xn
x
Уравнение касательной:
y  F ( x0 )  F ' ( x0 )( x  x0 )
Пусть y  0  0  F ( x0 )  F ' ( x0 ) ( x1  x0 )
F ( x0 )
x1  x0 
F ' ( x0 )
x 2  x1 
F ( x1 )
F ' ( x1 )
x n  x n 1 
F ( x n 1 )
F ' ( x n 1 )
xn  xn1 
2m1
M2
m1  min F ' ( x) m[ ,  ]
M 2  max F ' ' ( x) m[ ,  ]
x 0 выбирать так, чтобы F ( x0 ) * F ' ' ( x0 )  0
Пример:
F (x) = sin x – x + 0.15 = 0 на отрезке [0.5; 1] с погрешностью   10 4
F ' ( x)  cos x  1
sin x n 1  x n 1  0.15
x n  x n 1 
n  1, 2 , ...
cos x n 1  1
F ( x0 ) * F ' ' ( x0 )  0; F ' ' ( x)   sin x  0 для 0.5  x  1
То необходимо найти x 0 , чтобы F ( x0 )  0
Cos
0,5
Это верно при x 0 = 1
Sin
1
m1  min f ' ( x) на [0.5; 1]
F ' ( x)  cos x  1; m1  cos 0.5 1  0.88  1  0.12
m1  1  cos x  0.12
M 2  max F ' ' ( x) m[0.5;1]
F ' ' ( x)   sin x  M 2   sin 1  0.84
Примечание: если
2m1
 10 2 , то можно xn  xn1  10 1 
M2
1) x0  1;   10 3 , т.к.  1  10 1 10 4  10 3 ; n  0
sin xn  xn  0.15
cos xn  1
3) Вычисляем   xn1  xn
2) xn1  xn 
4) Проверяем    1 и так далее.
Случай почти равных корней
x0=x1
a1
a2
x1
x
Производная f ' ( x) близка к 1 при x  a1 или x  a2
f (a 2 )  f (a1 )
f ' ( x) 
1
a 2  a1
На основании теоремы о среднем
a  a2
x 1
2
Итерационный процесс осциллирует между x 0 и x1 до бесконечности, не сходясь ни к
одному значению корня. Другими словами – не удаётся отделить эти два корня, так как
они расположены слишком близко один к другому.
f ( xn )  xn f ( xn )
Трудности возникают, так как xn1 
, где 1  f ' ( xn )  0
1  f ' ( xn )
Мейкон (1963) предложил метод, согласно которому сначала находят значение x, где
f ' ( x)  1 , то есть решается уравнение: x  x  f ' ( x)  1
Пусть x  x - решение. Эта точка a1  x  a 2
Положим для начального приближения x 
Пусть d 
a1  a2
2
a2  a1
, т.е. a1  x  d и a2  x  d
2
Разложим f (x) в ряд Тейлора в окрестности точки x :
f ' ( x)
1
f ( x)  f ( x) 
( x  x)  f ' ' ( x)( x  x) 2  ...
1!
2!
1
Так как f ' ( x)  1 то f ( x)  f ( x)  ( x  x)  f ' ' ( x)( x  x) 2
2!
Пусть x  x  d
1
f ' ' ( x)d 2
2
Но по условию f ( x  d )  x  d
1
x  d  f ( x)  d  f ' ' ( x)d 2
2
f ( x  d )  f ( x)  d 
d
2( x  f ( x))
f ' ' ( x)
Если F ( x)  x  f ( x)  0, то F ' ' ( x)   f ' ' ( x) и d 
 2 F ( x)
, так как надо решить
F ' ' ( x)
уравнение F ' ( x)  0
x-d
x
x-d
Сначала решаем: x  x  f ' ( x)  1
Потом ищется: d 
2( x  f ( x))
f ' ' ( x)
Затем начальные приближения для a1 и a2
Если f ' ' ( x)  0 , то это означает что f ' ( x)  1 имеет более чем один корень вблизи x ,
тогда сначала решается уравнение f ' ' ( x)  0 , то это означает, что f ' ( x)  1 имеет более
чем один корень x .
Метод хорд
Каждое значение xn+1 находится как точка пересечения оси абсцисс с хордой, проведенной
через точки F(a) и F(b) , причем одна из этих точек фиксируется — та, для которой
F(x)·F''(x)>0.
Если неподвижен конец хорды x = a, то
F ( xn)
xn+1 = xn ( xn  a)
F ( xn)  F (a)
Если неподвижен конец хорды x = b, то
F ( xn)
(b  xn)
F (b)  F ( x)
Если |xn+1 - xn|>  ,то в первом случае считаем b = xn+1, во втором a = xn+1 и повторяем
вычисление.
При использовании метода хорд полагается, что корень x находится на отрезке [a,b].
xn+1 = xn -
Метод секущих
Реализуется алгоритмом, описанным выше, если абсцисса a и b взяты с одной стороны от
корня.
Необходимость вычисления F'(x) и выбора одной из двух формул затрудняют
практическое применение методов хорд и секущих в отдельности.
x2
a
x0=b
x
x1
F(x)
b0a1
b1a2
b2a3
x0
x1 x2 x3
x
Полином Чебышева
Применяется в уникальном процессе, называемом экономизацией, для преобразования
разложения функции в быстросходящийся полином.
Свойства полиномов Чебышева
1. Они являются ортогональными с соответствующей весовой функцией,
определенной либо на непрерывном интервале, либо на ряде дискретных
интервалов.
2. Они равно пульсирующие функции, то есть изменяются между равными
максимальными и минимальными значениями.
3. Нули полиномов Чебышева чередуются один за другим.
4. Все полиномы Чебышева удовлетворяют трехчленным рекуррентным
соотношением.
5. Они легко вычисляются и обращаются в форму степенного ряда на основании
исходной формы.
Все эти свойства образуют аппроксимирующую функцию минимакс (то есть в процессе
аппроксимации минимизируется максимальная ошибка)
В МНК минимизируется сумма квадратов ошибок. В МНК максимальная ошибка может
принимать достаточно большое значение. В аппроксимации Чебышева средняя ошибка
часто может принимать большое значение, а минимизируется максимальная ошибка.
Определение полиномов Чебышева
T0(x) = 1
Tn(x) = Cos(n  )
Cos  = x
Полиномы Чебышева ортогональны, так как косинус является ортогональной функцией и
Cos(n  ) является полиномом в степени n величин  .
Cos(n+1)  + Cos(n-1)  = 2Cos  Cosn 
Tn+1 + Tn-1 = 2xTn
Tn+1 = 2xTn - Tn-1
Так как T0 = 1; T1= x, то T2 = 2xT1 – T0 = 2x2 – 1
T3 = 2xT2 - T1 = 2x(2x2 – 1) – x = 4x3 – 3x
То есть T0 = 1
T1 = x
T2 = 2x2 – 1
T3 = 4x3 – 3x
T4 = 8x4 – 8x2 +1
T5 = 16x5 – 20x3 +5x
T6 = 32x6 – 48x4 + 18x2 -1
T7 = 64x7 – 111x5 +56x3 -7x
T8 = 128x8 – 256x6 +160x4 – 32x2 +1
Можно образовать таблицу степеней x в выражения полиномов Чебышева, проводя
решение относительно степеней x из этой таблицы:
1 = T0
x = T1
x2 = (T0 + T2)/2
x3 = (3T1 + T3)/4
x4 = (3T0 + 4T2 + T4)/8
x5 = (10T1 + 5T3 + T5)/16
x6 = (10T0 + 15T2 + 6T4 + T6)/32
x7 = (35T1 + 21T3 + 7T5 + T7)/64
x8 = (35T0 + 56T2 + 28T4 + 8T6 + T8)/128
Важное свойство полиномов Чебышева заключается в том, что во всех полиномах степени
n имеется коэффициент определение 1 и это полиномы Чебышева при делении на 2n-1
обладают наименьшим экстремальным значением в интервале -1  x  +1
Не существует других полиномов степени n, эти коэффициенты равны 1 и которые
обладают меньшим экстремальным значением, чем
Tn ( x )
1
max n 1  n 1 в интервале |x|  1
2
2
Это является важным положением, так как утверждает, что если аппроксимировать
функцию на интервале |x|  1 при помощи полиномов Чебышева, ограниченных n членами,
максимальной ошибкой приближения будет 1/2n-1
Разложим функцию f(x) в ряд с помощью полиномов Чебышева:
n
f(x) =
 a T ( x)
n n
n 0
Метод аппроксимации f(x) с помощью полиномов Чебышева является простым в
употреблении и обладает умеренной сходимостью любого ограниченного разложения
функции f(x) в ряд.
m
a x
Так как f(x) =
n
n
, то
n 0
f(x) = a0 + x(a1 +x(a2 + … + x(am-1 + am x))) …) — этот ряд можно привести к ряду
полиномов Чебышева, начиная от внутренних скобок, в виде
am-1 + am x = am-1 T0 + am T1
Можно умножить n скобочное гнездо:
a0T0 + a1T1 + … +anTn
на x и добавить к нему следующий коэффициент степени nm-n-1, чтобы получить (n+1)
гнездо.
Тогда применяя xT0 = T1; xTn = (Tn+1 + Tn-1)/2 приводим степенной ряд в n скобках,
осуществляя преобразование в (n+1) степенной ряд полиномов Чебышева следующим
образом:
anTn an  1Tn  1
a1  a 3
a2
a1

 ...  (
)T 2  (a 0  )T 1  (am  n  1  )T 0
2
2
2
2
2
Например:
N
fN(x) =
a x
N
n
n 0
f0 = a0
f1 = a0 + a1 x
a0 T0
a0 T0 + a1 T1
a2
a2
f2 = a0 + a1 x + a2 x2
(a0 +
)T0 + a1 T1 + ( )T2
2
2
a2
3a 3
a2
a3
f3 = a0 + a1 x + a2 x2+a3 x3
(a0 +
)T0 +( a1+
)T1 + ( )T2+( )T2
2
2
4
4
a 2 3a 3
3a 3
f4 = a0 + a1 x + a2 x2+a3 x3 + a4 x4
(a0 +
+
)T0 +(a1+
)T1a1+
2
8
4
1
a3
a4
 (a 2  a 4)T 2  ( )T 3  ( )T 4
2
4
8
a
2
3
a
3
3a 3 10a 5
f4 = a0 + a1 x + a2 x2+a3 x3 + a4 x4 +a5 x5
(a0 +
+
)T0 +( a1+
+
)T1+
2
16
8
4
a2  a4
a 3 5a 5
a4
a5
+(
)T2+ ( 
)T3+( )T4+( )T5
2
4 16
8
16
и т.д.
То есть можно вместо
f(x) = a0 + a1 x + a2 x2 +…+am xm
брать ряд f(x) = b0 + b1 T1 + b2 T2 +…+bm Tm
Для того, чтобы этот процесс был точным, ряд должен быть записан в такой форме, где
вычисляется f(x) при x (x)  1.
Пример:
x2 x3
y = ln(1+x)  x (1)

2
3
T0 T2
3T 1  T 3
y  T1 – (
)+(
)
4
12
T 0 15T 1 T 2 T 3



y(2)
4
12
4 12
Отбрасывая в (1) последний член, получаем погрешность (  ), равную 0,333 при x = 1.
А в ряд (2) при отбрасывании последних двух членов:
1 1
   = -00,1666… (так как Tn  1)
12 4
Таким образом, можно написать
T 0 15T 1 T 2

 , обеспечивающее лучшую точность, чем (1).
y = ln(1+x)  4
12
4
Теперь, используя определение полиномов Чебышева можно написать:
1 15 2 x 2 1
y = ln(1+x)   
 — это и есть экономизация.
4 12
4
4
Численная оценка полиномов Чебышева
Tn(x) = 2xTn-1(x) – Tn-2(x)
T0 = 1; T = x
T 0 15
T2 T2

y = ln(1+x)  -  T 1 
(3)
4 12
4 12
Можно оценить (3) первой оценкой численного значения для 4 полиномов Чебышева:
(пусть x = 0.3)
T0 = 1; T = 0.3
T2 = (2)(0.3)T1 – T0 = 2·0.3·0.3-1 = -0.82
T3 = (2)(0.3)T2 – T1 = -2·0.3·0.82 – 0.3 = 0.792
1 15
1
1
y = ln(1.3)    ( )0.3  (0.82)  (0.792)  0.2640
4 12
4
12
y = ln(1.3) = 0.26236426
Экономизируем разложение ряда Маклорена:
x2 x3 x4
x5
x6
ex = 1 + x +




 ...
2
6 24 120 720
1 = T0
x = T1
1
x 2= (T 0  T 2)
2
1
x 3= (3T 1  T 3)
4
1
x 4= (3T 0  4T 2  T 4)
8
1
(10T 1  5T 3  T 5)
x 5=
16
1
(10T 0  15T 2  6T 4  T 6)
x 6=
32
1
1
1
1
(3T 0  4T 2  T 4) 
(10T 1  5T 3  ...) +…
e x= T 0  T 1  (T 0  T 2)  (3T 1  T 3) 
4
24
192
1920
e x= 1.2661T0 + 1.1302T1 + 0.2715T2 + 0.0443T3 + …
e x= 1.2661 + 1.1302x + 0.2715(2x2 - 1) + 0.0444(4x 3– 3x) + …
e x  0.9946 + 0.9974x + 0.5430x2 + 0.1771x3 + …
x3 x5

6 120
1
1
(3T 1  T 3) 
(10T 1  5T 3  T 5)
Sin x = T1 24
1920
169
5
1
T1 
T3 
T5
Sin x =
192
128
1920
x5 изменяет коэффициент T1< на 1%, x7 - <0.01%
169
5
T1 
T3
Sin x =
192
128
T1 = x; T3 = 4x3 – 3x;
Sin x = 0.9974x – 0.1562x 3= x(0.9974 – 0.1562x2)
Sin x = x -
Маклор Ошибка
2·10-3
1·10-3
0
1·10-3
0,2
0,4
0,6
0,8
1