Нейронные сети обратного распространения ошибки Д.Е. Романов
advertisement

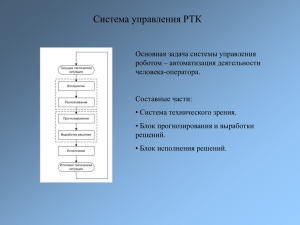
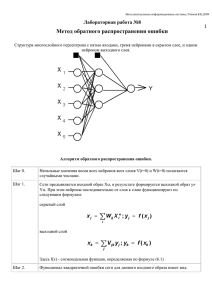
Нейронные сети обратного распространения ошибки Д.Е. Романов Южный федеральный Университет (РГУ), г. Ростов-на-Дону Идея искусственных нейронных сетей (ИНС) возникла, как попытка описать процессы восприятия информации, происходящие в мозге человека. Как и мозг человека, ИНС состоит из множества соединенных друг с другом элементов – нейронов, которые имитируют нейроны головного мозга. Существуют различные принципы построения сетей, или иначе, их архитектуры. Применительно к нейросетям иногда употребляется термин цитоархитектоника. Классическим примером архитектуры сети является нейросеть, в которой нейроны расположены по слоям и выходы одного слоя являются входами следующего. Однако, встречаются сети и с более сложной цитоархитектоникой, например, рекурсивные сети. В этой статье будут рассматриваться только многослойные сети прямого распространения, т.е. сети, в которых возбуждение передается лишь в одном направлении последовательно, от слоя к слою. Одной из моделей многослойной нейросети являются сети обратного распространения ошибки. Свое название эта модель сети получила благодаря специфическому алгоритму обучения. Рассматриваемый во многих источниках, он приведен слишком детально, что порой затрудняет восприятие сути алгоритма. Цель данной статьи – показать преимущество использования векторной арифметики для понимания принципов обучения нейросети обратного распространения ошибки. Кроме того, это позволяет нагляднее представить принцип функционирования многослойных нейросетей вообще. Рис. 1. Схема нейрона. Из рис. 1 видно, что искусственный нейрон, так же, как и живой, состоит из синапсов, связывающих входы нейрона с ядром; ядро нейрона, которое осуществляет обработку входных сигналов и аксона, который связывает нейрон с нейронами следующего слоя. Каждый синапс имеет вес, который определяет, насколько соответствующий вход нейрона влияет на его состояние. Коль скоро нейрон получает на свои входы суммарный сигнал, превышающий некоторое пороговое значение, на его аксоне формируется выходной сигнал. Таким образом, выход нейрона имеет следующий вид: of( w jij ) , j где f (x) – т.н. активационная функция, w j - вес j -го синапса, а i j - значение j -го входа нейрона. Наиболее часто в качестве активационной функции используется сигмоид, который имеет следующий вид: 1 f(x) 1ex Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную: f'( x ) f( x )( 1 f( x )) При уменьшении параметра сигмоид становится более пологим, вырождаясь в горизонтальную линию на уровне 0,5 при 0 . При увеличении сигмоид все больше приближается к функции единичного скачка [1]. Как уже было сказано, здесь будут рассматриваться только многослойные нейросети. Такая сеть строится из нескольких слоев нейронов. В пределах слоя нейроны не связаны, однако между соседними слоями нейроны соединяются по принципу «каждый с каждым» так, что выходы предыдущего слоя являются входами следующего. Если же нужно подчеркнуть отсутствие связи между какими-либо нейронами, то просто полагают вес данного синапса равным нулю. Рис. 2. Многослойная нейросеть. Следует остановиться на том, что понимают под слоем сети. В результате неразвитой терминологии нейронных сетей прошлых лет, резкой критики и непонимания задач исследования нейросетей, а иногда и ложного освещения прессой, изначальный смысл этого понятия исказился. В разных трактовках одна и та же сеть может называться и однослойной, и многослойной [2]. Здесь стоит вспомнить, что входной слой состоит, по сути, из нейронов-рецепторов, а однослойная сеть, состоящая лишь из таких нейронов, будет бесполезна. Поэтому следует рассматривать сети, состоящие как минимум из двух слоев – клеток-рецепторов и нейронов выходного слоя. Однако, как легко заметить, на первом слое никакой обработки информации не происходит. Поэтому удобнее считать лишь те слои нейронов, на которых происходит суммация возбуждения. В этом случае упомянутую выше двухслойную сеть следует называть однослойной. Для того чтобы сеть могла функционировать, ее необходимо обучить. Одним из алгоритмов обучения сетей является метод обратного распространения ошибки. Впервые этот метод был описан в 1974 г. А.И. Галушкиным, а также независимо и одновременно Полем Дж. Вербосом. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно С. И. Барцевым и В.А. Охониным (Красноярская группа). Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы нейронной сети и получения желаемого выхода [3]. Существенным условием применимости метода является дифференцируемость активационной функции. По сути, задача обучения НС сводится к нахождению некой функциональной зависимости O F(I ) , где I – входной, а O – выходной векторы. В общем случае такая задача при ограниченном наборе входных данных имеет бесконечное множество решений [1]. Для ограничения пространства поиска при обучении ставится задача минимизации целевой функции ошибки НС, которая находится, к примеру, по методу наименьших квадратов: E 1 (t kn okn ) 2 2 k где okn – значение k -го выхода нейросети, t kn – целевое значение k -го выхода, n – номер последнего слоя. Обучение нейросети производится методом градиентного спуска [4, с. 108], т.е. на каждой итерации изменение веса производится по формуле E k k w w i,j i,j k , w i,j где – параметр, определяющий скорость обучения, k 1..n – номер слоя. E Последняя задача сводится к вычислению частных производных wk ,k1..n. Это i,j легко сделать явно, раскрывая производную сложной функции. Для последнего уровня запись будет выглядеть следующим образом: E 1 n n2 n ( t o ) k k . n 2 w w k i ,j i ,j Т.к. по определению n n n 1 n n f( w i i,ko k ) on f(W o 1), o , k n n n то wi , j входит как множитель только в выражение t i oi . Это можно видеть из рис. 3. Рис. 3. 1n n2 ( t o 0 k i. k) n k Тогда очевидно, что 2 w при i,j Остается рассмотреть лишь случай k i . 1 n (t i oin ) 2 (t in oin ) n oin n wi , j 2 wi , j (t o ) n f ( win,k o kn 1 ) (t in oin )( )oin (1 oin )o nj 1 wi , j k n i . n i k Напомним также, что все o ,k 1..n нам известны (они получены при предъявлении обучаемого образа). Если сеть однослойная, то остается лишь скорректировать веса E n n w i,j i,j n . В противном случае необходимо продолжить согласно формуле w w i,j E ,kn 1 .. 1 . k W Для этого воспользуемся полученными выше результатами. Обозначим через E n1 n n n n ( t o ) o 1 o вектор с координатами . Тогда, к примеру, wn ioj , или в i i i)( i( i) i, j векторном виде E (on1)T (1) n W Вычислим E 1 n n2 n t o ) ( k k n 1 1 . 2 w w k i , j i , j вычисление Аналогично раскроем производную сложной функции 1n n n n 2 n t o ) ( t o )n o ( k k k k k , n 1 1 2 w w k k i , j i , j o n n 1 f ( wkn,l oln 1 ) n 1 k wi , j wi , j l n 1 o (1 o ) n 1 wkn,l oln 1 o kn (1 o kn ) wkn,l o l wi , j l win, j 1 l n k . n k Законность изменения порядка суммирования и дифференцирования непосредственно следует из линейности оператора дифференцирования. В итоге: 1 (t kn o kn ) 2 n 1 wi , j 2 k . n n n n n n n 1 n 1 k (t k ok )( )ok (1 ok )l wk ,l w n1 ol k k l wk ,l w n1 ol i, j i, j Легко заметить, что n 1 n 1n 2 o ( 1 o o i l n i ) j, 1 i o l , n 1 w 0 , i l i , j поэтому n E n n 1 n 1n 1 n 2 w o w ( ) o 1 o o k k , l l k , i k i( i) j, n 1 n 1 w w l k i , j k i , j или в векторной записи E n T n 1 n 1n 2 ( W ) * ( ) o * ( 1 o ) o , (2) n 1 W где под звездочкой понимается покоординатное умножение векторов. Обозначая через выражение, стоящее в квадратных скобках, можно последовательно найти все E ,kn2 .. 1 . k W Объединяя формулы (1) и (2), легко получить рекурсивную процедуру вычисления E всех (однако, как легко заметить, никакого «обратного распространения ошибки» не W k происходит, а название метода связано лишь с тем, что коррекцию весов матриц на каждом уровне удобнее производить, двигаясь от самого последнего уровня). Стоит отметить, что эта процедура позволяет выполнить лишь один шаг алгоритма градиентного спуска. Выбор параметра скорости обучения на каждом шаге можно осуществлять различными способами, например, из условия максимального убывания функции ошибки, или же считать постоянным, а шаги градиентного спуска выполнять до достижения некоторой степени точности решения одного примера. Но, вообще говоря, задача выбора размера шага является сложной и нетривиальной. Например, если размер шага фиксирован и очень мал, то сходимость будет слишком медленная; если же он фиксирован и слишком велик, то может возникнуть т.н. паралич сети (т.е. состояние, когда сеть теряет способность к обучению) или постоянная неустойчивость. В теоретическом отношении эта проблема изучена достаточно плохо [3]. Поэтому, как правило, параметры обучения сети подбираются экспериментально до достижения приемлемого результата распознавания образов. Литература. [1] http://www.basegroup.ru/library/analysis/neural/math/ [2] http://ru.wikipedia.org/wiki/Персептрон [3] http://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки [4] Лесин В.В., Лисовец Ю.П. Основы методов оптимизации.-М.: Изд-во МАИ, 1998.-344с. с ил.