Устойчивость линейных систем

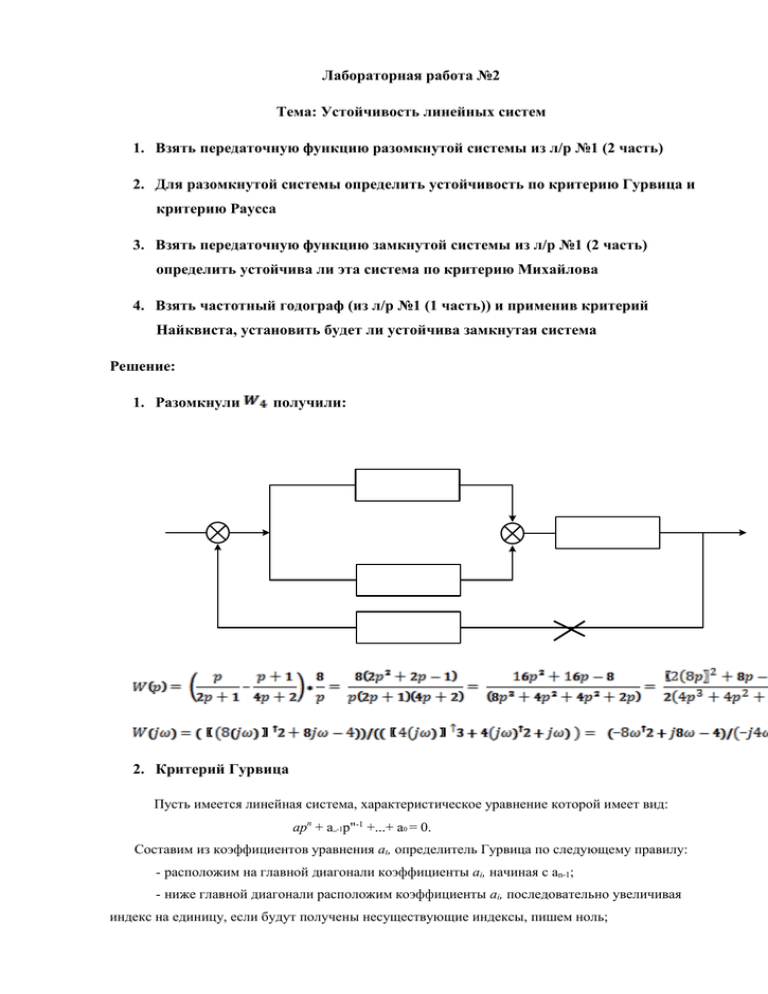
Лабораторная работа №2
Тема: Устойчивость линейных систем
1. Взять передаточную функцию разомкнутой системы из л/р №1 (2 часть)
2. Для разомкнутой системы определить устойчивость по критерию Гурвица и
критерию Раусса
3. Взять передаточную функцию замкнутой системы из л/р №1 (2 часть)
определить устойчива ли эта система по критерию Михайлова
4. Взять частотный годограф (из л/р №1 (1 часть)) и применив критерий
Найквиста, установить будет ли устойчива замкнутая система
Решение:
1. Разомкнули
получили:
2. Критерий Гурвица
Пусть имеется линейная система, характеристическое уравнение которой имеет вид:
apn + a„-1p"-1 +...+ a0 = 0.
Составим из коэффициентов уравнения at, определитель Гурвица по следующему правилу:
- расположим на главной диагонали коэффициенты ai, начиная с an-1;
- ниже главной диагонали расположим коэффициенты ai, последовательно увеличивая
индекс на единицу, если будут получены несуществующие индексы, пишем ноль;
- выше главной диагонали
расположим
коэффициенты ai, последовательно
уменьшая индекс на
единицу, если будут получены
несуществующие
индексы, пишем ноль
Формулировка критерия Гурвица:
Для устойчивости линейной системы автоматического управления необходимо и достаточно, чтобы при an>0 все главные диагональные миноры опеределителя Гурвица были
положительны.
Если все главные диагональные миноры положительны, а один из них равен 0, то система
является нейтральной.
Решение:
Таким образом, исследуемая система будет нейтральная, т.к. все главные диагональные
миноры положительны, а один из них равен 0.
3. Критерий Раусса
Критерий Раусса имеет ту же область применения, что и критерий Гурвица. Изменена
только сама математическая процедура проведения вычислений.
Пусть имеется линейная система, характеристическое уравнение которой имеет вид:
ap n + an-1pn-1 +...+ a0 = 0.
Построим из коэффициентов этого уравнения таблицу Раусса . Первые две строки таблицы
формируются из коэффициентов характеристического уравнения. При заполнении
следующих строк необходимо вычислить вспомогательные коэффициенты 1i. Если в
процессе
вычислений
встретится
несуществующий
индекс
коэффициента
характеристического уравнения, берется число 0. Всего таблица должна содержать n+1
строку.
Формулировка критерия Раусса:
Для устойчивости линейной системы необходимо и достаточно, чтобы все элементы
первого столбца таблицы Раусса были положительны.
Здесь под первым столбцом понимается столбец, содержащий значения Ci1.
Если все элементы первого столбца таблицы Раусса положительны, а один из них равен нулю, то
наша система нейтральна. Количество же перемен знака в первом столбце таблицы Ра-усса равно
количеству корней характеристического уравнения, лежащих в правой части комплексной
плоскости.
Решение:
Т.к.
, а все остальные элементы положительны, то система нейтральна
4. Критерий Михайлова
Пусть имеется линейная система, характеристическое уравнение которой имеет вид:
A(p)=anpn+an-1pn~J'+...+a0=0. Перейдем от комплексной переменной p к мнимому выражению
тогда наше выражение А(р) принимает вид A(
)=an (
может рассматриваться как частота. Изменяя 0 < <
геометрическое место точек конца вектора A(
)n+an-1 (
)n-1+...+a0, где величина
, построим годограф Михайлова -
при изменении частоты от 0 до
.
Формулировка критерия Михайлова:
Для устойчивости линейной системы автоматического управления необходимо и достаточно, чтобы годограф Михайлова, начинаясь на действительной, положительной полуоси
при изменении w от 0 до °°, последовательно, в положительном направлении (против часовой
стрелки) обходил n квадрантов, где n- порядок характеристического уравнения.
Рисунок 2
Примеры годографов Михайлова - а) неустойчивых систем; б) устойчивых систем
Решение:
,
Перейдем от
к
Строим годограф Михайлова
0
0
13
1
49
-53
2
50
-251
3
-45
-581
4
-284
-1043
5
-715
-1637
6
-1386
-2363
7
-2345
-3221
8
-3640
-4211
9
-5319
-5333
10
-7430
-6587
11
-10021
-7973
12
-13140
-9491
13
-16835
-11141
14
-21154
-12923
15
-26145
-14837
16
-31856
-16883
17
-38335
-19061
18
-45630
-21371
19
-53789
-23813
20
-62860
-26387
21
-72891
-29093
22
-83930
-31931
23
-96025
-34901
24
-109224
-38003
25
-123575
-41237
26
-139126
-44603
27
-155925
-48101
28
-174020
-51731
29
-193459
-55493
30
-214290
-59387
31
-236561
-63413
32
-260320
-67571
33
-285615
-71861
34
-312494
-76283
35
-341005
-80837
36
-371196
-85523
37
-403115
-90341
38
-436810
-95291
39
-472329
-100373
40
-509720
-105587
41
-549031
-110933
42
-590310
-116411
43
-633605
-122021
44
-678964
-127763
45
-726435
-133637
46
-776066
-139643
47
-827905
-145781
48
-882000
-152051
49
-938399
-158453
50
-997150
-164987
5. Критерий Найквиста
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по частотному
годографу разомкнутой системы. Поскольку частотный годограф может быть построен на
основании результатов измерений, то это единственный критерий позволяющий использовать
экспериментальные данные. Разомкнутая система может находиться в одном из трех состояний:
устойчивая, неустойчивая и нейтральная. Рассмотрим эти состояния более подробно.
5.1. Разомкнутая система находится в устойчивом состоянии.
Формулировка критерия Найквиста для этого случая принимает следующий вид: Для
устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф
разомкнутой системы при изменении частоты от 0 до
5.2. Разомкнутая система неустойчива.
не охватывал точку (-1;0).
Формулировка критерия Найквиста для этого случая принимает следующий вид: Для
устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф
разомкнутой системы при изменении частоты от 0 до
охватывал точку (-1;0) L/2 раз, где L -
количество корней характеристического уравнения, принадлежащих правой части комплексной
плоскости.
5.3. Разомкнутая система нейтральна.
Формулировка критерия Найквиста для этого случая принимает следующий вид: Для
устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф
разомкнутой системы при изменении частоты от 0 до
, с учетом дополнения в
бесконечности, не охватывал точку (-1;0).
Дополнением в бесконечности называется дуга бесконечно большого радиуса с центром в
начале координат, проведенная от положительной действительной полуоси по часовой стрелке до
пересечения с годографом.
Решение:
0
-0,2
0
1
-0,06897
0,172414
2
0,013699
0,150685
3
0,038128
0,088388
4
0,041509
0,037736
5
0,038356
0,00274
6
0,033557
-0,02013
7
0,028774
-0,03457
8
0,024529
-0,04335
9
0,020929
-0,04841
10
0,017931
-0,05103
11
0,01545
-0,05208
12
0,013396
-0,05211
13
0,011691
-0,0515
14
0,010267
-0,05049
15
0,009072
-0,04924
16
0,008062
-0,04785
17
0,007204
-0,04641
18
0,006469
-0,04495
19
0,005837
-0,04351
20
0,00529
-0,04209
21
0,004813
-0,04073
22
0,004397
-0,03941
23
0,00403
-0,03815
24
0,003706
-0,03695
25
0,003419
-0,03581
26
0,003163
-0,03472
27
0,002935
-0,03368
28
0,002729
-0,03269
29
0,002544
-0,03175
30
0,002377
-0,03086
31
0,002226
-0,03001
32
0,002088
-0,0292
33
0,001963
-0,02843
34
0,001848
-0,02769
35
0,001743
-0,02699
36
0,001647
-0,02633
37
0,001558
-0,02569
38
0,001476
-0,02508
39
0,001401
-0,02449
40
0,001331
-0,02393
41
0,001266
-0,0234
42
0,001205
-0,02289
43
0,001149
-0,0224
44
0,001097
-0,02192
45
0,001048
-0,02147
46
0,001002
-0,02103
47
0,000959
-0,02062
48
0,000919
-0,02021
49
0,000881
-0,01982
50
0,000846
-0,01945
Судя по тому что частотный годограф разомкнутой системы при изменении частоты от 0 до
,
с учетом дополнения в бесконечности, не охватывал точку (-1;0), разомкнутая система нейтральна.