Тема: Площадь криволинейной трапеции. (Интегрированный
advertisement

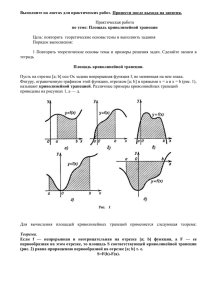
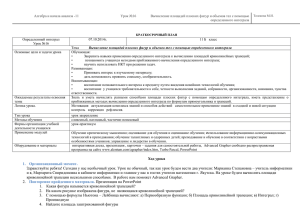
Тема: Площадь криволинейной трапеции. (Интегрированный урок алгебры в 11 классе) Нет ни одной области математики, как бы абстрактна она не была, которая когда-нибудь не окажется применимой к явлениям действительного мира. Н. И. Лобачевский. Цели - повторить понятие криволинейной трапеции; - вычисление площадей криволинейных трапеций с помощью первообразных функций; - вычисление первообразных функций с помощью составленных программ; - развитие интереса к предмету на основе межпредметных связей; - провести вычислительный эксперимент по нахождению площади фигур методом МонтеКарло. Интеграция: математика – информатика – теория вероятности. Ход урока. 1. Вступительное слово учителя. Мы собрались на необычный урок, где мы убедимся, что математика, как бы абстрактна она не была, окажется применимой к явлениям действительного мира. Как можно реализовать численные методы с помощью ЭВМ. Что уроки информатики, на которых составлялись различные алгоритмические программы, сегодня понадобятся нам для вычисления площадей криволинейных трапеций. Как математическая модель. Выбранная нами для решения задач на вычисление площадей фигур, отличается от предыдущих тем. Что там используются случайные числа, т.е. вероятностные модели. 2. Повторение. Вопрос 1. Какую фигуру называют криволинейной трапецией? ( Фигура, ограниченная снизу осью абсцисс, сверху графиком непрерывной Функции у = f(x), принимающей положительные значения, а с боков прямыми Х = а и х = в, называют криволинейной трапецией.) Вопрос 2. Как вычисляются площади криволинейных трапеций? ( Площадь криволинейной трапеции вычисляем по формуле Ньютона-Лейбница: S = ∫abf(x)d(x) = F(b) – F(a)) Вопрос 3.( Устно) Как вы будете вычислять площади фигур, изображенных на рисунках? ( 1. S = ∫13x2 dx 2. S = ∫0πsinx dx ) 3. Сейчас мы с вами рассмотрим пример вычисления площадей более сложных фигур, ограниченных графиками двух функций с помощью компьютера. Пример 1. Найти площадь фигуры, ограниченной графиками у = х – 2, у = х2 – 4х + 2. Решение. Построим графики функций у = х – 2, у = х2 – 4х + 2. Найдем абсциссы пересечения этих графиков, решив уравнение: х – 2 = х2 – 4х + 2. Уравнение имеет корни 1 и 4. Тогда, S = ∫14 (x – 2 – x2 + 4x – 2)dx = 4,5. Пример 2. Составить формулы для вычисления площадей по рисункам. а) б) в) S = = ∫ab (f2(x) – f1(x))dx S = ∫abf1(x)dx + ∫abf2(x)dx + ∫abf3(x)dx S = ∫ab (f1(x) – f3 (x))dx + ∫ab (f2(x) – f3(x))dx 4. Самостоятельная работа по вычислению площадей криволинейной трапеции. Но вычисление площади криволинейной трапеции вы будете осуществлять по составленной вами программе нахождения первообразных некоторых функций. Учащиеся получают карточки с заданиями: 1) Вычислить площадь криволинейной трапеции, ограниченной линиями: а) у = 9 – 3х2, осью абсцисс и прямыми х = - 1, х = 1; б) у = 0,5х3 + 1, осью абсцисс и прямыми х = 1, х = 2. Программа для вычисления первообразных степенных функций. 10. Площадь криволинейной трапеции. 20. INPИТ «Введите границы интегрирования a, b», А, В. 30. INPИТ «Введите коэффициент перед х, показатель степени х», С, N. 40. INPИТ «Введите свободный член» к. 50. х = В, GOSHP : FI = Г. 60. х = А, , GOSHP: 100 : F2 = F 70. S = FI – F2. 80 . PRINT: «Площадь криволинейной трапеции = S». 90. END. 10. А = С ∙ хА (N + 1)/(N + 1) + кх. 11. RETИPV. 5. В математике часто для решения задач требуются математические модели. Одна из таких задач – вычисление площадей фигур. Конечно, для простейших фигур вычисление площадей не составляет труда. Вопрос: Площади каких фигур мы умеем вычислять? ( Треугольника, квадрата, прямоугольника, параллелограмма, ромба, трапеции, круга с помощью известных формул.) Математическую модель, которую мы сейчас построим, может показаться вам неожиданной, но она позволяет очень эффективно применить ЭВМ для решения задач на вычисление площадей фигур. Поместим фигуру в прямоугольник. Будем наугад, т.е. случайным образом, бросать точки в этот прямоугольник. Вопрос: В каком случае большая часть точек будет попадать в заданную фигуру? ( Естественно предполагать, что чем больше площадь фигуры, тем чаще в неё будут попадать точки.) Такой метод приближенного нахождения площади фигур носит название метода Монте-Карло. (По названию города. Где расположена знаменитая рулетка, которую можно рассматривать как «генератор» случайных чисел.) В чем он состоит. Пусть проводится серия из N одинаковых опытов. При этом интересующее нас событие А появилось NА раз, NА ˂ N. Относительной частотой появления события А называется число µ(А) = NА/ N. Остальную часть урока и будет посвящена вычислительным экспериментам по нахождению площадей фигур методом Монте-Карло. у = sinАх. 1) А = 0,3; NА = 15; N = 150, 2) А = 1,52; NА = 15; N = 150. Наша задача выяснить, от чего будет зависеть точность результата. ( Чем больше N, тем заметнее, что µ(А) стабилизируется возле некоторого, вполне определенного числа. Р(А) ≈ µ(А).) Итог урока. Вопрос: От каких величин и в какой взаимосвязи зависит точность вычислений? Задание: Вычислить вероятность попадания в часть нашей фигуры через отношение площади указанной части ко всей фигуре.