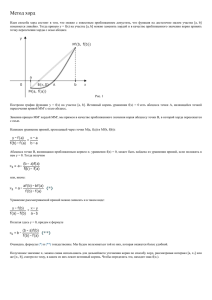
1.4. Метод хорд
advertisement

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОУВПО «Самарский государственный архитектурно-строительный
университет»
Факультет информационных систем и технологий
Кафедра прикладной математики и вычислительной техники
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ
по дисциплине
ТЕХНОЛОГИЯ ПРОФЕССИОНАЛЬНОЙ ДЕЯТЕЛЬНОСТИ
на тему
«Визуализация процесса нахождения корней нелинейных
уравнений методом Бройдена»
5 СЕМЕСТР 3 КУРС
Научный руководитель (ФИО)
Преподаватель (ФИО)
Методический руководитель (ФИО)
Бойцев Александр
Филиппов И.С., Шинкарев Г.Г.
Пиявский С.А.
Выполнил:
студент ГИП-107 Давыдова Евгения
подпись
Оценка преподавателя
_______________
Оценка комиссии по результатам защиты_______________
2009 г.
дата
УДК 004.021
Расшифровка:
Наука в целом (информационные технологии - 004)Информационные
технологии.
Компьютерные технологии. Теория вычислительных машин и систем
Методы решения задач
Алгоритмы составления программ
Ключевые слова
Алгоритм, Бройдена, метод, решение, уравнения, информационная, система
Реферат
Существует несколько методов решения нелинейных уравнений. В
данной работе рассмотрены такие, как метод деления отрезка пополам, метод
простой итерации, метод Ньютона (касательных), метод хорд,
комбинированный метод и метод Бройдена. Комбинированный метод (метод
хорд и касательных) является одним из оптимальных методов решения
нелинейных уравнений. Метод Бройдена также имеет одни из лучших
результатов. Это видно после исследования методов. По-этому, возникла
задача, целью которой является написание программы, визуализирующую
процесс нахождения корней нелинейных уравнений методом Бройдена. В
процессе написания программы были реализованы два способа графического
представления данного метода (пошаговый и стандартный).
Экран оценки творческого уровня работы
Аннотация
Существует несколько методов решения нелинейных уравнений. В
данной работе рассмотрены такие, как метод деления отрезка пополам, метод
простой итерации, метод Ньютона (касательных), метод хорд,
комбинированный метод и метод Бройдена. Метод секущих Бройдена
является одним из оптимальных методов решения нелинейных уравнений.
По-этому, возникла задача, целью которой является написание программы,
визуализирующую процесс нахождения корней нелинейных уравнений
методом Бройдена.
Наиболее простым методом, позволяющим найти корень нелинейного
уравнения, является метод половинного деления. Сходимости мала, но к
достоинствам метода относятся простота и безусловная сходимость
итерационного
процесса.
Метод
Ньютона
(Касательных)
имеет
квадратичную скорость сходимости. Он является одним из оптимальных
методов, так же как и комбинированный метод приближения корня
уравнения по методу хорд и по методу касательных подходят к значению
этого корня с противоположных сторон. Поэтому для быстроты нахождения
корня удобно применять оба метода одновременно. Т.к. один метод даёт
значение корня с недостатком, а другой – с избытком, то достаточно легко
получить заданную степень точности корня.
Решение нелинейных уравнений комбинированным методом возможно
только при выполнении следующих условий:
1) f (a ) f (b) 0 ,
2) f (x) и f (x ) сохраняют знак на отрезке a; b ,
Приближения корней находятся:
а) по методу касательных: x11 x0 f ( x0 ) ,
f ( x0 )
б) по методу хорд: x12 a (b a) f (a) .
f (b) f (a)
При схождении к корню с разных сторон скорость схождения
получается максимальной.
В процессе написания программы были реализованы два способа
графического представления данного метода (пошаговый и стандартный).
Программа написана в интегрированной среде программирования
Delphi 8.0 на языке Pascal. По средствам парсера формул функция
преобразовывается в код, затем уравнение решается методом хорд и
касательных. После достижения заданной точности выполняется построение
графика пошагово и полностью. Парсер был реализован созданием
специального класса.
При исследовании сходимости методов решения нелинейных
уравнений метод Хорд и касательных оказался наиболее оптимальным из
выбранных методов. На втором месте оказался метод Ньютона.
Содержание:
1. Методы решения нелинейных уравнений
1.1. Метод деления отрезка пополам
1.2. Метод простой итерации
1.3. Метод Ньютона (касательных)
1.4. Метод Хорд
1.5. Комбинированный метод
1.6. Метод простейших секущих
1.7. Метод секущих Бройдена
2. Выявление наиболее оптимального метода
3. Алгоритм решения уравнения комбинированным методом
4. Программа визуализации процесса нахождения корней нелинейных
уравнений комбинированным методом и методом Бройдена.
5. Список литературы
1. Методы решения нелинейных уравнений
1.1 Метод деления отрезка пополам
Наиболее простым методом, позволяющим найти корень нелинейного
уравнения, является метод половинного деления.
Пусть на отрезке [a, b] задана непрерывная функция y f (x ). Если
значения функции на концах отрезка имеют разные знаки, т.е.
f (a) * f (b) 0, то это означает, что внутри данного отрезка находится
нечетное число корней. Пусть для определенности корень один. Суть метода
состоит в сокращении на каждой итерации вдвое длины отрезка. Находим
c (a b) / 2. Вычисляем значение
функции f (c) и выбираем тот отрезок, на котором функция f (x) меняет
середину отрезка [a,b] (см. рис. 1)
свой знак. Новый отрезок вновь делим пополам. И этот процесс продолжаем
до тех пор, пока длина отрезка не сравняется с наперед заданной
погрешностью
вычисления
корня
.
Построение
нескольких
последовательных приближений по формуле (3) приведено на рисунке 1.
Итак, алгоритм метода дихотомии:
1. Задать отрезок [a,b] и погрешность .
2. Если f(a) и f(b) имеют одинаковые знаки, выдать сообщение о
невозможности отыскания корня и остановиться.
y
y=f(x)
f(a)
a c4 = c *
f(b)
c3
c2
c1
b
x
Рис.1. Метод деления отрезка пополам для решения уравнения вида
f(х)=0.
3. В противном случае вычислить c=(a+b)/2
4. Если f(a) и f(c) имеют разные знаки, положить b=c, в противном
случае a=c.
5. Если длина нового отрезка b a , то вычислить значение корня
c=(a+b)/2 и остановиться, в противном случае перейти к шагу 3.
Так как за N шагов длина отрезка [a, b] сокращается в 2N раз, то
заданная погрешность отыскания корня будет достигнута за итераций.
ln b a /
ba
N log 2
ln 2
Как видно, скорость сходимости мала, но к достоинствам метода
относятся простота и безусловная сходимость итерационного процесса. Если
отрезок [a, b] содержит больше одного корня (но нечетное число), то всегда
будет найден какой-нибудь один.
Замечание. Для определения интервала, в котором лежит корень,
необходим дополнительный анализ функции y f (x) , основанный либо на
аналитических оценках, либо на использование графического способа
решения. Можно также организовать перебор значений функции в различных
точках, пока не встретится условие знакопеременности функции
f (x ).
1.2 Метод простой итерации
При использовании этого метода исходное нелинейное уравнение (1)
необходимо переписать в виде
x g(x)
(2)
Обозначим корень этого уравнения C*. Пусть известно начальное
x C
0 . Подставляя это значение в правую часть
приближение корня
уравнения (2), получаем новое приближение
C1 g (C 0 )
и т.д. Для (n+1)- шага получим следующее приближение
C n 1 g (C n )
(3)
Таким образом, по формуле (3) получаем последовательность С0,
С1,…,Сn+1, которая стремиться к корню С* при n. Итерационный процесс
прекращается, если результаты двух последовательных итераций близки, т. е.
выполняется условие
С n 1 С n .
(4)
Исследуем
условие
и
скорость
сходимости
числовой
последовательности {C n} при n. Напомним определение скорости
сходимости. Последовательность {Cn}, сходящаяся к пределу С*, имеет
скорость сходимости порядка , если при n выполняется условие
n1 С n1 С* O С n С* O n .
(5)
Допустим, что g (x ) имеет непрерывную производную, тогда
погрешность на (n+1)-м итерационном шаге n+1=Cn+1-C*=g(Cn)-g(C*) можно
представить в виде ряда
n+1 Cn+1 – C* = g(C*) (Cn-C*) + g(C*) n+
Таким образом, получаем, что при выполнении условия
g(C*)
(6)
последовательность (3) будет сходиться к корню с линейной скоростью
. Условие (6) является условием сходимости метода простой итерации.
Очевидно, что успех метода зависит от того, насколько удачно выбрана
функция g (x ) .
Например, для извлечения квадратного корня, т. е. решения уравнения
вида x =a2, можно положить
x=g1(x)=a/x
(7а)
или
x=g2(x)=(x+a/x)/2.
(7б)
Нетрудно показать, что
g1'(C)=1,
g2'(C)<1.
Таким образом, первый процесс (7а) вообще не сходится, а второй (7б)
сходится при любом начальном приближении С0 >0.
y
0
y=x
c* c 2 c 1
y=g(x)
c0
x
Рис. 2. Графическая интерпретация метода простых итераций для
решения уравнения вида x=g(х).
Построение нескольких последовательных приближений по формуле
(3)
С0, С1, …, Сn = C*
приведено на рисунке 2.
1.3 Метод Ньютона (Касательных)
В литературе этот метод часто называют методом линеаризации.
Выбираем начальное приближение С0. Допустим, что отклонение С0 от
истинного значения корня С* мало, тогда, разлагая f(C*) в ряд Тейлора в
точке С0 , получим
f(C*) = f(C0) + f (C0) (C*-C0) +
(8)
Если f (C0) 0 , то в (8) можно ограничится линейными по C =C-C0
членами. Учитывая, что f(C*)=0, из (9) можно найти следующее приближение
для корня
C1 = C0 – f (C0) / f(C0)
или для (n+1)-го приближения
Cn+1= C n – f (C n) / f (C n)
(9)
Для окончания итерационного процесса можно использовать одно из
двух условий
Cn+1 – Cn
или
f(Cn+1) .
Исследование сходимости метода Ньютона проводится аналогично
предыдущему случаю. Самостоятельно получить, что при выполнении
условия
f ''(C)/2f'(C)<1.
метод Ньютона имеет квадратичную скорость сходимости (
2 ).
y
y=f(x)
c1
0
c2
c*
c0
x
Рис. 3. Графическая интерпретация метода Ньютона для решения
уравнения вида f(х)=0.
Построение нескольких последовательных приближений по формуле
(9)
С0, С1, …, Сn = C*
приведено на рисунке 3.
1.4. Метод хорд
Данный способ можно свести к следующему алгоритму:
1. Разделим всю область исследования (Df) отрезки, такие, что внутри
каждого отрезка [x1;x2] функция монотонная, а на его концах
значения функции (x1) и (x2) разных знаков. Так как функция
(x) непрерывна на отрезке [x1;x2], то ее график пересечет ось ОХ в
какой либо одной точке между x1 и x2.
2. Проведем хорду АВ, соединяющую концы кривой y = (x),
соответствующие абсциссам x1 и x2. Абсцисса a1 точки пересечения
этой хорды с осью ОХ и будет приближенным значением корня. Для
разыскания этого приближенного значения напишем уравнение
прямой АВ, проходящей через две данные точки A(x1;(x1)) и B(x2;
(x2)), в каноническом виде:
y f ( x1 )
x x1
;
f ( x2 ) f ( x1 ) x2 x1
Учитывая, что y = 0 при x = a1, выразим из данного уравнения a1:
a1
x1 f ( x2 ) x2 f ( x1 )
f ( x2 ) f ( x1 )
(1)
3. Чтобы получить более точное значение корня, определяем (а1). Если
на данном отрезке мы имеем (x1)<0, (x2)>0 и (a1)<0, то повторяем
тот же прием, применяя формулу (1) к отрезку [a1;x2]. Если (x1)>0,
(x2)<0 и (a1)>0, то применяем эту формулу к отрезку [x1;a1].
Повторяя этот прием несколько раз, мы будем получать все более
точные значения корня а2, а3 и т.д.
1.5 Комбинированный метод (метод хорд и касательных)
Если выполняются условия:
1) f (a ) f (b) 0 ,
2) f (x) и f (x ) сохраняют знак на отрезке a; b ,
то приближения корня x a; b уравнения f ( x) 0 по методу хорд и по
методу касательных подходят к значению этого корня с противоположных
сторон. Поэтому для быстроты нахождения корня удобно применять оба
метода одновременно. Т.к. один метод даёт значение корня с недостатком, а
другой – с избытком, то достаточно легко получить заданную степень
точности корня.
1.6. Метод простейших секущих
Можно связать задание последовательности ( h (k ) ) с какой-либо
сходящейся к нулю векторной последовательностью, например, с
последовательность невязок ( F ( x (k ) ) ) или поправок ( p (k ) ). Так, полагая
h (j k ) : x (jk 1) x (jk ) где j=1,…n, a k=1,2,…,приходим к простейшему методу
секущих — обобщению скалярного метода секущих (5.32):
1
(4.1.1)
x ( k 1) x ( k ) B( x ( k ) , x ( k 1) ) F ( x ( k ) ) ,
где
n
f i ( x1( k ) ,..., x (jk 1) ,..., x n( k ) ) f i ( x1( k ) ,..., x (jk ) ,..., x n( k ) )
(k )
( k 1)
B( x , x
) :
( k 1)
(k )
x
x
j
j
i , j 1
k=1,2,3,….
Этот метод является. двухшаговым и требует задания двух начальных
точек x ( 0 ) и x (1) . При п = 1 сходимость метода(4.1.1) имеет порядок
1 5
.
2
Можно рассчитывать на такую же скорость и в многомерном случае.
К методу секущих так же, как и к методу Ньютона, можно применить
пошаговую аппроксимацию обратных матриц на основе метода Шульца.
Расчетные формулы этой модификации легко выписать, заменив в
совокупности формул ААМН (3.3.1) матрицу F ( x ( k 1) ) на матрицу B( x ( k 1) , x ( k ) )
из (4.1.1)
1.7. Метод секущих Бройдена
В процессе построения методов Ньютона и секущих решения
нелинейного скалярного уравнения
f ( x, y ) 0
функция f(x) в окрестности текущей точки x k подменяется линейной
функцией
(4.4.1)
k (ak , x) : f ( xk ) ak ( x xk )
(4.4.1а)
Приравнивание к нулю последней, т.е. решение линейного уравнения
f ( xk ) ak ( x xk ) 0 ,
порождает итерационную формулу
x k 1 x k a k1 f ( x k )
(4.4.2)
для вычисления приближений к корню уравнения (4.4.1).
Если потребовать, чтобы заменяющая функцию f(x) вблизи точки x k
аффинная модель k (a k , x) имела в этой точке одинаковую с ней
производную, то, дифференцируя (4.4.1а), получаем Значение коэффициента
ak f ( xk ) ,
подстановка которого в (4.4.2) приводит к известному методу Ньютона. Если
же исходить из того, что наряду с равенством k (ak , x) f ( xk ) должно иметь
место совпадение функций f(x) и k (a k , x) в предшествующей x k точке xk 1 т.е.
из равенства
k (ak , xk 1 ) f ( xk 1 ) ,
или, в соответствии с (4.4.1а)
f ( xk ) a k ( xk 1 xk ) f ( xk 1 ) ,
(4.4.3)
то получаем коэффициент
ak
f ( xk 1 ) f ( xk )
,
xk 1 xk
превращающий (4.4.2) в известную формулу секущих.
Равенство (4.4.3), переписанное в виде
ak ( xk 1 xk ) f ( xk 1 ) f ( xk ) ,
называют соотношением секущих в R1 Оно легко обобщается на n -мерный
случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.
В n-мерном векторном пространстве Rn соотношение секущих
представляется равенством
Bk ( x ( k 1) x ( k ) ) F ( x ( k 1) ) F ( x ( k ) ) ,
(4.4.4)
( k 1)
(k )
где x , x — известные n-мерные векторы, F : Rn Rn — данное
нелинейное отображение, а Bk — некоторая матрица линейного
преобразования в Rn . С обозначениями
(k )
(k )
( k 1)
)
s ( k ) : x ( k ) x ( k 1) , y : F ( x ) F ( x
(4.4.5)
соотношение секущих в Rn обретает более короткую запись:
Bk s ( k ) y ( k )
(4.4.4а)
Аналогично одномерному случаю, а именно, по аналогии с формулой
(4.4.2), будем искать приближения к решению x * векторного уравнения (2.1а)
по формуле
(4.4.6)
x ( k 1) x ( k ) Bk1 F ( x ( k ) )
Желая, чтобы эта формула обобщала метод секущих (5.32), обратимую
n x n-матрицу Bk в ней нужно подобрать так, чтобы она удовлетворяла
соотношению секущих (4.4.4). Но это соотношение не определяет
однозначно матрицу Bk : глядя на равенство (4.4.4а), легко понять, что при
n>1 существует множество матриц Bk , преобразующих заданный n-мерный
вектор s (k ) в другой заданный вектор y (k ) (отсюда — ясность в понимании
того, что могут быть различные обобщения одномерного метода секущих).
При формировании матрицы Bk будем рассуждать следующим
образом.
Переходя от имеющейся в точке x ( k 1) аффинной модели функции F(x)
k 1 : F ( x ( k 1) ) Bk 1 ( x x ( k 1) )
(4.4.7)
(k )
к такой же модели в точке x
k : F ( x ( k ) ) Bk ( x x ( k ) )
(4.4.8)
мы не имеем о матрице линейного преобразования Bk никаких сведений,
кроме соотношения секущих (4.4.4). Поэтому исходим из того, что при этом
переходе изменения в модели должны быть минимальными. Эти изменения
характеризует разность k k 1 . Вычтем из равенства (4.4.8) определяющее
k 1 равенство (4.4.7) и преобразуем результат, привлекая соотношение
секущих (4.4.4). Имеем:
k k 1 : F ( x ( k ) ) F ( x ( k 1) ) Bk ( x x ( k ) ) Bk 1 ( x x ( k 1) )
Bk ( x ( k ) x ( k 1) ) Bk x ( k ) Bk 1 x ( k 1) ( Bk Bk 1 ) x ( Bk Bk 1 )( x x ( k 1) )
Представим вектор x x ( k 1) в виде линейной комбинации
фиксированного вектора s (k ) определенного в (4.4.5), и некоторого вектора t,
ему ортогонального:
R1 , t Rn : (t , s ( k ) ) 0.
x x ( k 1) s ( k ) t ,
Подстановкой этого представления вектора x x ( k 1) в разность k k 1
получаем другой ее вид
(4.4.9)
k k 1 ( Bk Bk 1 ) s ( k ) ( Bk Bk 1 )t
Анализируя выражение (4.4.9), замечаем, что первое слагаемое в нем не
может быть изменено, поскольку
( Bk Bk 1 ) s ( k ) Bk s ( k ) Bk 1 s ( k ) y ( k ) Bk 1 s ( k )
- фиксированный вектор при фиксированном k. Поэтому минимальному
изменению аффинной модели k 1 будет отвечать случай, когда второе
слагаемое в (4.4.9) будет нуль-вектором при Iвсяких векторах t,
ортогональных векторам s (k ) , т.е. Bk следует находить из условия
(4.4.10)
( Bk Bk 1 )t 0
t : (t , s ( k ) ) 0 .
Непосредственной проверкой убеждаемся, что условие (4.4.10) будет
выполнено, если матричную поправку Bk Bk 1 взять в виде одноранговой
nхn-матрицы
Bk Bk 1
( y ( k ) Bk 1 s ( k ) )( s ( k ) ) T
(s (k ) )T
(k )
.
Таким образом, приходим к так называемой формуле пересчета С.
Бройдена (1965 г.)
Bk Bk 1
( y ( k ) Bk 1 s ( k ) )( s ( k ) ) T
(s (k ) )T s (k )
(4.4.11)
которая позволяет простыми вычислениями перейти от старой матрицы Bk 1 к
новой Bk такой, чтобы выполнялось соотношение секущих (4.4.4а) в новой
точке и при этом изменения в аффинной модели (4.4.7) были минимальны
Совокупность формул (4.4.6), (4.4.11) вместе с обозначениями (4.4.5)
называют методом секущих Бройдена или просто методом Бройдена
решения систем нелинейных числовых уравнений.
Хотя в методах секущих обычным является задание двух начальных
векторов ( x ( 0 ) и x (1) ), для метода Бройдена характерно другое начало
итерационного процесса. Здесь нужно задать один начальный вектор x ( 0 ) ,
начальную матрицу B0 и далее в цикле по k = 0,1,2,... последовательно
выполнять следующие операции:
1.
решить линейную систему
(4.4.12)
Bk s ( k 1) F ( x ( k ) )
относительно вектора s ( k 1) :
2.
найти векторы x ( k 1) и y ( k 1) :
(4.4.13)
x ( k 1) x ( k ) s ( k 1) , y ( k 1) F ( x ( k 1) ) F ( x ( k ) ) ;
3.
сделать проверку на останов (например, с помощью проверки
на малость величин s ( k 1) и/или y ( k 1) и если нужная точность не
достигнута, вычислить новую матрицу Bk по формуле пересчета (см.
(4.4.11))
Bk 1 Bk
( y ( k 1) Bk s ( k 1) )( s ( k 1) ) T
( s ( k 1) ) T s ( k 1)
(4.4.14)
В качестве матрицы B0 , требуемой равенством (4.4.12) для запуска
итерационного процесса Бройдена, чаще всего берут матрицу Якоби F ( x (0) )
или какую-нибудь ее аппроксимацию. При этом получаемые далее
пересчетом (4.4.14) матрицы B1 , B2 ,... не всегда можно считать близкими к
соответствующим матрицам Якоби F ( x (1) ) , F ( x ( 2) ) ,... (что может иногда
сыграть полезную роль при вырождении матриц F ( x * ) ). Но, в то же время,
показывается, что при определенных требованиях к матрицам Якоби F (x)
матрицы Bk обладают «свойством ограниченного ухудшения», означающим,
что если и происходит увеличение Bk F ( x (k ) ) с увеличением номера
итерации k, то достаточно медленно. С помощью этого свойства
доказываются утверждения о линейной сходимости ( x ( k ) ) к х*
при достаточной близости x ( 0 ) к х* и B0 к F ( x (0) ) а в тех предположениях,
при которых можно доказать квадратичную сходимость метода Ньютона
(3.1.2), — о сверхлинейной сходимости последовательности приближений по
методу Бройдена.
Как и в случаях применения других методов решения нелинейных
систем, проверка выполнимости каких-то условий сходимости итерационного
процесса Бройдена весьма затруднительна.
Формуле пересчета (4.4.14) в итерационном процессе
придать чуть более простой вид.
Так как, в силу (4.4.12) и (4.4.13),
y ( k 1) Bk s ( k 1) F ( x ( k 1) ) F ( x ( k ) ) F ( x ( k ) ) F ( x ( k 1) ) ,
а
2
2
(s ( k 1) ) T s ( k 1) (s ( k 1) , s ( k 1) ) s ( k 1) x ( k 1) x ( k ) ,
2
2
можно
то из формулы (4.4.14) получаем формально эквивалентную ей
формулу пересчета
Bk 1 Bk
F ( x ( k 1) )( x ( k 1) x ( k ) ) T
x ( k 1) x ( k )
2
(4.4.14а)
,
2
которую можно использовать вместо (4.4.14) в совокупности с формулой
(4.4.6) или с (4.4.12), (4.4.13) (без вычисления вектора y ( k 1) ). Такое
преобразование итерационного процесса Бройдена несколько сокращает
объем вычислений (на одно матрично-векторное умножение на каждой
итерации). Не следует, правда, забывать, что при замене формулы (4.4.14)
формулой (4.4.14а) может измениться ситуация с вычислительной
устойчивостью метода; к счастью, это случается здесь крайне редко, а
именно, в тех случаях, когда для получения решения с нужной точностью
требуется много итераций по методу Бройдена, т.е. когда и применять его
не стоит.
2. Выявление наиболее оптимального метода
Для выявления наиболее оптимального метода решения нелинейных
уравнений были решены 10 различных уравнений предложенными методами.
В таблицу было выписано количество шагов сходимости для каждого метода:
Методы
Бройдена
Комбинированный
Хорд
Ньютона
Простых итераций
Деления пополам
1
4
5
6
5
7
8
2
6
4
7
6
7
9
3
3
5
6
6
8
7
4
5
4
6
6
7
8
5
3
5
6
5
6
8
6
4
3
7
7
7
8
7
5
5
9
6
9
11
8
5
4
7
8
8
9
9
3
5
8
6
7
10
10
4
3
7
5
8
7
По результатам таблицы была составлена гистограмма в которой
можно заметить, что Комбинированный метод и метод Бройдена имеют
самую быструю сходимость:
Скорость сходимости методов
15
10
Бройдена
Комбинированный
Хорд
Ньютона
10
7
4
0
1
5
Простых итераций
Деления пополам
Для наиболее четкого результата были подсчитаны и сравнены средние
значения:
Методы
Бройдена
Комбинированный
Хорд
Ньютона
Простых итераций
Деления пополам
Среднее
4,2
4,3
6,9
6
7,4
8,5
Сравнение средней продолжительности сходимости методов
11%
23%
12%
18%
20%
16%
Бройдена
Комбинированный
Хорд
Ньютона
Простых итераций
Деления пополам
На круговой диаграмме хорошо видно, что Комбинированный метод и
метод Бройдена являются наиболее оптимальными, так как имеют самую
быструю сходимость. Второе место занимает метод Ньютона. Далее метод
Хорд, простых итераций и деления пополам.
3. Алгоритм решения уравнения комбинированным методом
1. Вычислить значения функции f (a ) и f (b ) .
2. Проверить выполнение условия f (a ) f (b) 0 . Если условие не
выполняется, то неправильно выбран отрезок a; b .
3. Найти производные f (x) и f (x ) .
4. Проверить постоянство знака производных на отрезке a; b . Если нет
постоянства знака, то неверно выбран отрезок a; b .
5. Для метода касательных выбирается за x0 тот из концов отрезка a; b ,
в котором выполняется условие f ( x0 ) f ( x0 ) 0 , т.е. f ( x0 ) и f ( x0 )
одного знака.
6. Приближения корней находятся:
а) по методу касательных: x11 x0 f ( x0 ) ,
f ( x0 )
б) по методу хорд: x12 a (b a) f (a) .
f (b) f (a)
7. Вычисляется первое приближение корня: x x .
11
1
12
2
8. Проверяется выполнение условия: 1 x11 , где - заданная
точность.
Если условие не выполняется, то нужно продолжить применение метода
по схеме 1-8.
В этом случае отрезок изоляции корня сужается и имеет вид x11 ; x12 .
Приближённые значения корня находятся по формулам:
x21 x11
f ( x11 )
f ( x11 )
и
x22 x11
( x12 x11 ) f ( x11 ) .
f ( x12 ) f ( x11 )
Вычисления продолжаются до тех пор, пока не будет найдено такое значение
, при котором xn1 и xn 2 совпадут с точностью .
4. Программа визуализации процесса нахождения корней нелинейных
уравнений методом секущих Бройдена.
Библиографический список
1. Методические указания
к выполнению лабораторных работ по
дисциплине
«Методы оптимизации и принятия решений» /
С.А.Пиявский; Самарск. гос. арх.-строит. ун-т./ Самара, 2007.
2. «Учебник по Delphy 7», Семенов П.А. ,Москва, 2007 г.
3. Приближённое решение алгебраических и трансцендентных уравнений
[Электронный ресурс] // Режим доступа: http://www.allbest.ru.
4. «Методы решения нелинейных уравнений», Попов А.В. , Москва, 2008 г.
5. Графические возможности среды программирования Borland Delphi 7.0 //
Режим доступа: http://www.sumdelphu.ru.
6. Применение парсера формул // Режим доступа: http://www.delphipars.ru.
7. «Статистический анализ линейных величин», Васильев Л.П., Зимин В.Н. ,
Москва 2009 г.
8.
Решение систем нелинейных уравнений методом секущих // Режим
доступа: http://www.strimplovers.ru.