Document 739446

Раздел I.
Алгебра и геометрия
Раздел I. Алгебра и геометрия
Е.С. Арапина-Арапова
О КАТЕНАРНЫХ ИНВЕРСНЫХ ПОЛУГРУППОИДАХ
Понятие катенарного полугруппоида ввел в геометрических целях В.В. Вагнер [2]. Полугруппоидом называется сильно ассоциативный частичный группоид, т.е. частичный группоид
(S ;) является полугруппоидом тогда и только тогда, когда из того, что определено в S одно из
произведений ( x  y )  z , x  ( y  z ) следует, что определено и другое, и выполняется равенство
(1)
( x  y)  z = x  ( y  z ) .
Если произведение u  v не определено в S , то пишем u  v   .
Очевидно, частичный группоид ( S ;) есть полугруппоид тогда и только тогда, когда его
нулевое расширение [3]
S 0  S  {0}
является полугруппой. Поэтому всякое свойство полу-
группоидов влечет очевидное следствие для полугрупп (с нулем).
Идемпотентный коммутативный полугруппоид называем частичной полурешеткой.
Идемпотентный частичный группоид называется антицепью, если условие
гда влечет
xy  
все-
x  y.
(S ;) называют
( x  y)  z    x  ( y  z ) .
Частичный группоид
всегда влечет
катенарным, если условие
Условие катенарности частичного группоида группоида
x y    yz
S равносильно условию катего-
0
рийности в нуле его нулевого расширения S .
Принятая полугрупповая терминология сохраняется нами и для произвольных полугруппоидов. Понятны, например, термины регулярный, инверсный, простой, вполне простой полугруппоиды и т.д. Вполне простой инверсный полугруппоид называют группоидом Брандта.
  обозначен класс всех полугруппоидов S , на которых существует такая конгруэнция  , что S   , а каждый замкнутый в

S  -класс принадлежит  . Всякий полугруппоид класса   называем  -полугруппоидом
 – полугруппоидов. В работе рассматривается строение катенарных полугруппоидов, являющихДля произвольных классов
, 
полугруппоидов через
ся идемпотентными коммутативными полугруппоидами группоидов Брандта. Частным случаем полученного в работе результата является одна из основных теорем в [1].
Обозначения:
А – класс антицепей;
В – класс группоидов Брандта;
I – класс полурешеток;
Q – класс катенарных частичных полурешеток
M – класс инверсных клиффордовых полугруппоидов, в которых идеальная эквивалентность Грина
 является конгруэнцией;
К – класс тех полугруппоидов
S М, для которых бинарное отношение
 {( ,  )  S  S      }


3
Вестник ТГПИ
Естественные науки
удовлетворяет условию
(   &    )  (     )
(2)
Теорема 1. Q=I  А
S I  А, т.е. S – прямое объединение полурешеток, то идемпотентность и коммутативность полугруппоида S очевидны. Пусть x, y, z  S , xy    yz . Тогда,
Доказательство. Если
по определению (  ) и класса А, элементы
лугруппоида
Значит
S
x, y, z
S , а поэтому ( xy) z ( x( yz ))
принадлежат некоторой подполурешетке
принадлежит
S
по-
S , т.е. ( xy ) z    x( yz ) .
– катенарный идемпотентный коммутативный полугруппоид, т.е. S – катенарная частичная
S Q. Итак, I  А  Q.
Докажем обратное включение. Если S Q, то отношение   {( x, y )  S  S xy  }
полурешетка, следовательно,
является эквивалентностью. В самом деле, рефлексивность и симметричность

следуют соответ-
S . Если, наконец xy , yz, т.е
xy    yz , то, в силу катенарности, ( xy) z   . Но S – полугруппоид, поэтому
( xz ) y  ( zx) y  z ( xy )   . Отсюда следует xz . Значит,  – эквивалентность на S . По
ственно из идемпотентности и коммутативности умножения в
 , если xy , то xy   , т.е. xy  S . Но x  ( xy )  x 2 y  xy   , поэтому
x (xy) . Таким образом, каждый  – класс есть обычный (т.е. полный) группоид, а поэтому является обычной полурешеткой. Из сказанного следует S I  А. Этим доказано включение Q  I  А, а
определению
вместе с ним и требуемое равенство.
В [4] доказано, что полугруппоиды класса К и только они являются катенарными частичными полурешетками группоидов Брандта, т.е. К=В  Q, откуда, по теореме 1, К=В  (I  А). Естественно, возникает вопрос о строении катенарных полугруппоидов класса К. Решение этого вопроса и является целью настоящей работы.
Теорема 2. Полугруппоид
 ,   S  , таких, что   
потент
f 
f  e.
Доказательство. Пусть S
S
класса К катенарен тогда и только тогда, когда для любых
и любого идемпотента
e 
найдется единственный идем-
такой, что
катенарный полугруппоид из К. В этом случае, как показано в
S К и указанe, f , g  S такие,
[4] обозначенное в формулировке условие выполнено. Покажем обратное. Пусть
ное в формулировке условие выполнено. Берем произвольные идемпотенты
что
ef    fg
и покажем, что
efg  
(3)
Y группоидов Брандта {   Y }. Следовательно найдутся такие  ,  ,   Y , что e   , f   , g   . Поскольку ef    fg
Т.к.
S К, то S
является частичной полурешеткой
то, по определению частичного факторгруппоида
частичная полурешетка
Очевидно
Т.к.
4
Y
S

катенарна, то отсюда следует
 Y , имеем          . Т.к.
      .
      .
ef     , то по условию, найдется идемпотент h1      
(4)
такой, что
Раздел I.
Алгебра и геометрия
h1  ef  f
Аналогично, существует идемпотент
h2      
h1  fg  f
Но
     В,
т.е
   
h1  h2 .
.
(5)
такой, что
.
– группоид Брандта и
h1 , h2      
   
, значит либо
h1h2   ,
либо
идемпотенты
h1 , h2 , удовлетворяющие (5), (6) и выполняется неравенство (4), что противоречит
Если
h1  h2 ,
(6)
то в группоиде
требованию «единственности» в формулировке теоремы. Значит
h1  h2 , откуда получаем
  h1  h12  h1h2  h1 (ef )  ( fg )h2  h1 (efg )h2 , поскольку S
да следует
efg   .
нашлись различные
Таким образом, в инверсной полугруппе
полугруппоид. Отсю-
S 0  S  {0}
идемпотентов категорийна в нуле, а потому категорийна в нуле и полугруппа
поид
S
полурешетка
S  , т.е. полугруп-
катенарен.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Арапина–Арапова Е.С. Разложение полугрупп в объединение декартовых полугрупп // II–я Международная конференция «Полугруппы: теория и приложения» в честь профессора Е.С. Ляпина. СПб, 1999.
С. 66–67.
2. Вагнер В.В. Диаграммируемые полугруппоиды и обобщенные группоиды. Известия вузов, Математика, 1967. № 10. С. 11–23.
3. Клиффорд А., Престон Г. Алгебраическая теория полугрупп // Мир, М., 1972. Т. 1,2.
4. Кожевников О.Б. Об одной операции на классах полугруппоидов. Вестник ТГПИ, Естест. науки, 2009.
Д.А. Жуков
О ЖЕСТКОСТИ ПОВЕРХНОСТИ, СКЛЕЕННОЙ ИЗ КУСКОВ ПОВЕРХНОСТЕЙ
НЕОТРИЦАТЕЛЬНОЙ ГАУССОВОЙ КРИВИЗНЫ,
ОТНОСИТЕЛЬНО БЕСКОНЕЧНО МАЛЫХ AG-ДЕФОРМАЦИЙ
1. Формулировка результата.
Предметом исследования данной работы являются замкнутые поверхности, звездные относительно некоторой точки, лежащей внутри поверхности, склеенные из гладких кусков поверхностей неотрицательной гауссовой кривизны (каждый кусок класса
C m , m  2 ), причем гауссова
кривизна может быть равна нулю только в конечном числе изолированных точек и вдоль некоторых кривых.
Исследование ведется в трехмерном евклидовом пространстве.
Ставится задача: изучить поведение такой поверхности относительно бесконечно малых
AG-деформаций, считая, что поле деформации непрерывно на всей поверхности, а на гладких кусках поле деформации принадлежит классу
Рассмотрим поверхность S:
Cm, m  2 .
r  r (u, v)  C m , m  2, (u, v)  D .
Определение 1. Бесконечно малыми AG-деформациями поверхности называют такие бесконечно малые деформации, которые сохраняют поточечно сферический образ поверхности
5
Вестник ТГПИ
( n
Естественные науки
 0 ) и элемент площади поверхности (  (d )  0 ), где n 
тор нормали к поверхности,
[ru , rv ]
[ru , rv ]
d  EG  F 2 dudv  [ru , rv ] dudv
– единичный век-
– элемент площади
поверхности.
{S }: r  r   y , где
Рассмотрим бесконечно малые AG-деформации поверхности S.
y
– поле бесконечно малой AG-деформации, причем
Тогда
довательно,
n  n , d  d  , то есть
S  S0 .
[ru , rv ] [r u , r v ]

[ru , rv ] [r u , r v ]
и
[ru , rv ]  [ r u , r v ] . Сле-
[ru , rv ]  [ru , r v ] , тогда
[ru , rv ]  [(r   y )u ,(r   y )v ]  [ ru   yu , rv   yv ,] 
 [ru , rv ]   ([ru , yv ]  [ yu , rv ])   2[ yu , yv ].
Рассмотрение ведется с точностью до второго порядка по ε, поэтому получаем:
[ru , rv ]  [ru , rv ]   ([ru , yv ]  [ yu , rv ]) ,
[rv , yu ]  [ru , yv ]  0 .
(1)
Определение 2. Уравнение (1) называется уравнением бесконечно малых AG-деформаций в
векторной форме.
Определение 3. Уравнение (1) всегда допускает решения вида
ное поле вида
y  C  const
y  C  const . Вектор-
будем называть тривиальной бесконечно малой AG-
деформацией.
Определение 4. Если поверхность не допускает иных бесконечно малых AG-деформаций,
кроме тривиальных, то она называется жесткой относительно бесконечно малых AG-деформаций.
Сформулируем основной результат работы.
Теорема. Пусть  – замкнутая поверхность, звездная относительно некоторой точки О,
лежащей внутри нее, склеенная из гладких кусков поверхностей неотрицательной гауссовой кри-
C m , m  2 ), причем гауссова кривизна может быть равна нулю
только в конечном числе изолированных точек и вдоль некоторых кривых. Тогда поверхность 
визны (каждый из них класса
является жесткой относительно бесконечно малых AG-деформаций.
2. Вспомогательные утверждения.
Лемма 1. Для поверхности S:
нечно малой AG-деформации
r  r (u, v)  C m , m  2, (u, v)  D , и поля ее беско-
y  C m , m  2 справедливы формулы:
 yu   ru   rv ,

 yv   ru   rv ,
где  ,  ,  – некоторые скалярные функции от u, v.
Доказательство.
Воспользуемся уравнением бесконечно малой AG-деформации в векторном виде:
[rv , yu ]  [ru , yv ] .
6
(2)
Раздел I.
Алгебра и геометрия
Умножая это равенство скалярно на ru
и rv , находим
(rv , yu , ru )  0, (ru , yv , rv )  0.
Следовательно, векторы ru и rv компланарны с векторами
разложить векторы
yu
и
yv
yu
и
yv . Значит мы можем
по векторам ru и rv , тогда
 yu   ru   rv ,

 yv   ru   rv .
 ,  ,  , – некоторые скалярные функции от u, v
Подставив эти выражения в [ rv , yu ]  [ ru , yv ] , получим:
[rv , ru   rv ]  [ru ,  ru   rv ] ,
 [rv , ru ]   [rv , rv ]   [ru , ru ]   [ru , rv ] ,
 [rv , ru ]   [ru , rv ]  0 ,
 [ru , rv ]   [ru , rv ]  0 ,
(   )[ru , rv ]  0 .
По условию
[ru , rv ]  0 , следовательно,    .
Откуда следуют формулы (2).
Лемма доказана.
Лемма 2. Коэффициенты второй квадратичной формы L, M, N поверхности S:
r  r (u, v)  C m , m  2, (u, v)  D ,
связаны со скалярными функциями
 ,  ,   C1
следующим соотношением:
L  2M  N   0 .
(3)
Доказательство.
Рассматриваемая поверхность удовлетворяет условию леммы 1, значит для нее справедливы
соотношения (2). Продифференцируем первое из них по v, а второе по u:
yuv   v ru   ruv  v rv   rvv ,
yvu   u ru   ruu  u rv   rvu .
В силу условия
yuv  yvu , имеем
 v ru   ruv  v rv   rvv   u ru   ruu   u rv   rvu  0 .
Умножив полученное выражение скалярно на единичный вектор нормали
n , учитывая, что
(ru , n )  (rv , n )  0 , получим
 (ruv , n )   (rvv , n )   (ruu , n )   (rvu , n )  0 .
Откуда следует формула (3).
Лемма доказана.
Известен следующий результат (см. напр. [3]).
Лемма 3.
L  2M  N   0, то    2    0 . Равенство
  0 возможно тогда и только тогда, когда       0 .
Если
LN  M 2  0
и
7
Вестник ТГПИ
Естественные науки
Лемма 4. Для бесконечно малых AG-деформаций поверхности справедлива интегральная
формула
2 (r , n )d    (r , y , d y ) ,
S
S
где S – гладкая поверхность с радиус-вектором
ее граница,
n
r  r (u, v)  C m , m  2, (u, v)  D , S
– единичный вектор нормали к поверхности S,
нечно малой AG-деформации,
u, v , при этом обход S
   2   ,  ,  , 
–
y  C m , m  2 , – поле беско-
– некоторые скалярные функции от
производится в направлении, оставляющем поверхность слева.
Доказательство:
Очевидны тождества

(r , yu , y )  (rv , yu , y )  (r , yuv , y )  (r , yu , yv ),
v

(r , yv , y )  (ru , yv , y )  (r , yvu , y )  (r , yv , yu ).
u
Вычитая из первого уравнения второе и учитывая уравнение (1), получим:


(r , yu , y )  (r , yv , y )  2(r , yu , yv )  (rv , yu , y )  (ru , yv , y ) 
v
u
 2(r , yu , yv )  ([rv , yu ]  [ru , yv ], y )  2(r , yu , yv ).
То есть получили следующее равенство:


(r , yu , y )  (r , yv , y )  2(r , yu , yv ) .
v
u
(4)
Полагая теперь в формуле Грина
 Q P 
D  u  v  dudv  D Pdu  Qdv
P  (r , yu , y ), Q  (r , yv , y )
и учитывая равенство (4), получим

 

2 (r , yu , yv )dudv    (r , yv , y )  (r , yu , y ) dudv 
u
v

D
D 
   (r , yu , y )du  (r , yv , y )dv    (r , yu du  yvdv, y )    (r , d y , y )   (r , y , d y ) .
D
D
D
D
Получили формулу:
2 (r , yu , yv )dudv 
D
 (r , y , d y ).
(5)
D
Используя формулы (2), преобразуем подынтегральное выражение левой части формулы (5):
(r , yu , yv )  (r , ru   rv ,  ru   rv )  (r , [ru , ru ]   2[ru , rv ]   [rv , ru ]   [rv , rv ]) 
 (r ,  2[ru , rv ]   [rv , ru ])  (r ,( 2   )[ru , rv ])  ( 2   )(r , ru , rv ).
Формула (5) примет вид:
2 (r , ru , rv ) dudv 
D
8
 (r , y , d y ).
D
(6)
Раздел I.
Алгебра и геометрия
Умножим и разделим выражение, стоящее в левой части равенства (6) под знаком интеграла,
на
[ru , rv ] :
2 (r ,
D
[ru , rv ]
)  [ru , rv ] dudv   ( r , y , d y ) .
[ru , rv ]
D
Откуда следует, что
2 (r , n )  d    (r , y , d y ) .
S
S
Лемма доказана.
 , склеенной из гладких кусков поверхностей положительной
m
2
гауссовой кривизны (каждый из них класса C , m  2 ), величина      сохраняет
Лемма 5. На поверхности
знак, а именно
  0 , где  ,  ,   C1 на каждом гладком куске.
Доказательство:
Возьмем любой из гладких кусков, составляющих поверхность  , например
влетворяет условию леммы 2, поэтому для него справедлива формула (3).
Из положительности гауссовой кривизны следует, что
влетворяет условию леммы 3, следовательно,
Это означает, что на  имеем
Лемма доказана.
3. Доказательство теоремы.
0
на
  0 , то есть 
S
1
LN  M 2  0 , поэтому S 1
сохраняет знак на всей поверхности

.
склеена из двух кусков
S 2 , удовлетворяющих условию теоремы.
Выберем начало координат в точке О, относительно которой поверхность
звездной. Выберем на поверхности такую ориентацию, что
удо-
.
Для простоты доказательства будем считать, что поверхность
и
S 1 . Он удо-

является
(r , n )  0 на  , единичный вектор
S 1  S 2 – общая граница S 1 и S 2 .
Теперь вычислим интеграл по поверхности  :
 (r , n )d   (r , n )d   (r , n )d .
нормали
n
S1
направлен вне поверхности.

S
1
S
(7)
2
Но в силу леммы 4:
 (r , n )  d  
S1
1
(r  , y  , d y  ),

2 S 1
1
 (r , n )  d   2  (r
, y  , d y  ).
S 2
S2
Здесь

r  , y  , d y  ; r  , y  , d y  – предельные значения r , y , d y
на
S1 и S 2
со-
ответственно. Далее имеем:
r   r  на S 1  S 2 в силу непрерывности поверхности  ;
y   y  на S 1  S 2 в силу непрерывности поля деформации y
на поверхности
;
9
Вестник ТГПИ
Естественные науки
dy dy 
вдоль
S 1  S 2
в направлении
S 1  S 2 ,
так как
y  y
на
S 1  S 2 .
Тогда равенство (7) примет вид:
 (r , n )d  


1
1



(
r
,
y
,
d
y
)

(r  , y  , d y  ) 


2 S 1
2 S 2
1
1
(r  , y  , d y  )   (r  , y  , d y  )  0.

2 S 1
2 S 1
То есть
 (r , n )d  0.
(8)

В силу леммы 5   0 на
Рассмотрим два случая.
 , при К > 0 на каждом из гладких кусков поверхностей.
S 1 имеет К > 0, за исключением некоторой точки М, в которой К = 0.
2
Мы уже увидели, что когда К > 0, то       0 . Предположим, что в точке М
Пусть поверхность
(где К = 0)
   2    0 .
Так как
   2  
непрерывно, то
   2    0 в некоторой окрестности
точки М. Возьмем еще меньшую окрестность точки М, вложенную в первую окрестность, и выбросим ее. У нас осталось кольцо, в котором, по предположению
в нем К > 0. Но тогда по лемме 3
предположение, что в точке M
   2    0 , при этом
   2    0 . Получили противоречие. Значит наше
   2    0 , неверно, и    2    0
в точке
М, в которой К = 0.
Рассмотрим теперь некоторую кривую (l) на поверхности
S1 ,
вдоль которой К = 0, при
равна нулю. Предположим, что в некоторой точке
  0 . Итак, вдоль кривой гауссова кривизна
M 0 этой кривой   0 .
   2   ,
получаем, что в некоторой окрестности точки
этом на остальной поверхности
В силу непрерывности
S
1
К > 0, а значит
M 0   0 . В этой окрестности всегда можно выбрать точку M 1 , не лежащую на кривой (l).
Всегда можно указать такую окрестность точки
M 1 , что она будет целиком лежать в окрестности
M 0 , и при этом не будет содержать точек кривой (l). Но во всех точках, не лежащих на
кривой, К > 0, а следовательно, там имеем   0 . Получается, что с одной стороны, в окрестности точки M 1   0 , а с другой стороны   0 . Получили противоречие. Значит наше предточки
положение, о том, что в некоторой точке
сти выбора точки
M0
кривой (l)
  0 , неверно и, в силу произвольно-
M 0 , в каждой точке кривой (l), вдоль которой К = 0, имеем   0 .
0
S 1 , и когда К =
1
1
0 вдоль некоторой кривой на поверхности S , следовательно   0 на всей поверхности S .
2
Аналогично доказывается, что   0 на поверхности S .
Итак,
10
и в случае, когда К = 0 в изолированных точках поверхности
Раздел I.
Алгебра и геометрия
  0 на  , то есть  сохраняет знак на  . При этом выполнено соотношение (8), (r , n )  0 на  , в силу выбора ориентации, d  0 – элемент площади  . Эти
условия выполняются одновременно только при   0 на  .
1
2
Следовательно,   0 на каждом из гладких кусков (на S и S ).
1
Рассмотрим S . В силу леммы 3   0 тогда и только тогда, когда       0 .
Таким образом,
Тогда на
где
S 1 имеют место равенства:
1
1

 yu   r u   r v  0,
 y  C1  const ,

1
1
y


r


r

0.

u
v
 v
r 1 – радиус-вектор поверхности S 1 .
1
Следовательно, поверхность S является жесткой
относительно бесконечно малых AG-
деформаций.
Аналогично доказывается жесткость поверхности
Из непрерывности поля деформации
 . Это означает, что вся поверхность 
S2.
y  y  C1  C2  const
на всей поверхности
является жесткой относительно бесконечно малых AG-
деформаций.
Теорема доказана.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Векуа И. Н. Обобщенные аналитические функции. М.: Наука, 1988. С. 378–384.
2. Мокрищев К. К. Введение в теорию бесконечно малых изгибаний поверхностей. Ростов-н/Д., 1961.
С. 14–17.
3. Розендорн Э. Р. Теория поверхностей. М.: ФИЗМАТЛИТ, 2006. С. 238–266.
Е.А. Коломыцева
О КОРРЕКТНЫХ ВТУЛОЧНЫХ СВЯЗЯХ
ARG -ДЕФОРМАЦИЯХ ПОВЕРХНОСТЕЙ
3
В РИМАНОВОМ ПРОСТРАНСТВЕ R
ПРИ БЕСКОНЕЧНО МАЛЫХ
R 3 – трёхмерное риманово пространство с координатами y (  1,2,3)
ds 2  a dy dy  , где a  C 4, , 0    1 , F 2 - (m  1) -связная поверх-
П.1. Пусть
и метрикой
ность с краем, заданная уравнениями
y  f   x1 , x 2  ,   1,2,3,  x1 , x 2   D ,
f   x1 , x 2  - функции класса C 3, ( D) . Пусть, далее, граница D
области
D
где
принадлежит
C 2, , 0    1 . Эти условия будем называть условиями регулярности поверхности. Будем считать, что внешняя кривизна поверхности положительна K  k0  0 , k0  const . Расклассу
смотрим бесконечно малую деформацию
уравнениями
y  y   z , где z
её деформации,

F  , F
2

2
0
 F2 ,
поверхности
F2 ,
определяемую
F 2 при
z  z  zn ,
– векторное поле смещения точек поверхности
– малый параметр. Представим поле смещения в виде суммы
11
Вестник ТГПИ
Естественные науки
z  ai y,i
где
ющая
z
поля
z , zn  cn
– тангенциальная составляющая поля

,
n

–
поле
единичных
векторов
нормалей
– нормальная составляк
поверхности
y
y,i  i , i  1,2 .
x
F2 ,

Бесконечно малую деформацию
{F 2 }
поверхности
мацией [1], если выполняются условия: 1) вариация
сти
F2
называют
элемента площади
ARG -дефорd поверхно-
удовлетворяет соотношению
 (d )  2 Hcd ,

где
 (d )
F2
– заданное число, называемое коэффициентом рекуррентности,
поверхности
F
2
; 2) для любой точки поверхности
F
2
H
– средняя кривизна
её единичный вектор нормали
n , па-
R 3 в смысле Леви-Чивита в направлении вектора z в соответству2

2
ющую точку поверхности F , совпадает с вектором нормали n к F в этой точке.
Внешней связью поверхности при её ARG -деформации называют условие, при котором

2
поле смещения z на некотором множестве G точек поверхности F обладает наперед задан2
ными свойствами. Обычно, в качестве множества G выбирают край поверхности F , то есть
G  F 2 , а в качестве внешней связи соотношение вида:
(1)
R  z   h на F 2 ,
раллельно перенесенный в
R  z 
где
h
– заданный линейный оператор,
– заданная функция.
При
h  0 внешнюю связь называют однородной.
Внешняя связь называется корректной [2], если для любой функции
ственное поле смещения
ции
h
z

h
существует един-
, удовлетворяющее условию (1), при этом малому изменению функ-
соответствует малое изменение поля
z .
Внешняя связь называется некорректной [2], если при h  0 поверхность допускает бесконечно малые деформации лишь при выполнении конечного числа условий разрешимости, налагаемых на функцию h , а при h  0 поверхность допускает конечное число линейно независимых бесконечно малых деформаций.
Зададим на краю
F 2
поверхности
F2
отличное от нуля векторное поле
l   l  ln ,

где l
 l i y,i
щая поля
– тангенциальная составляющая поля
l  , l1 , l 2 , l 3
конечно малые
– заданные функции класса
(2)
l  , ln  l 3n
– нормальная составляю-
C 1, , 0    1 . Будем рассматривать бес-
ARG -деформации поверхности F 2 , подчиненной на краю F 2
a z l  =h ,
условию
(3)
где h – заданная функция класса C , 0    1 . Это условие назовём условием обобщенной
втулочной связи.
Для формулировки результата введем в рассмотрение правый сопровождающий трех1,
гранник Френе
12
{t  ,  , n }
края
F 2
поверхности
F 2 , где t 
- поле единичных векторов
Раздел I.
Алгебра и геометрия
касательных к краю
F
2
,
n
F 2 ,  
– поле единичных векторов тангенциальных нормалей к краю

– поле единичных векторов нормалей к краю
Имеет место следующая
F 2 .
(m  1) -связная поверхность F 2 положительной внешней кривизны
K  k0  0 , k0  const , в римановом пространстве R 3 удовлетворяет условиям регулярности,
ориентирована так, что средняя кривизна H  0 , и подвергнута бесконечно малой ARG 2
деформации с заданным коэффициентом рекуррентности  ,    . Пусть, далее, поверхность F

i 
3 
2
подчинена на краю F условию обобщенной втулочной связи (3), где поле l  l y,i l n та
i 
ково, что его тангенциальная составляющая l  l y,i образует тупой угол с тангенциальной
Теорема. Пусть

F 2 , координата l 3  0 . Тогда эта связь является корректной в
1,
классе C , 0    1 , в отношении бесконечно малых ARG -деформаций с заданным коэф1,

фициентом рекуррентности  ,   . Причем поле смещения z принадлежит классу C ,
0    1 , а его нормальная составляющая c принадлежит классу C 2, , 0    1 .
нормалью
края поверхности
ARG -деформации поверхноK  k0  0 , k0  const . Здесь и далее в этой
П.2. Выведем уравнение, описывающее бесконечно малые
сти
F
2
положительной внешней кривизны
работе будем считать, что на поверхности введена изотермически-сопряженная параметризация,
то есть вторая квадратичная форма поверхности имеет вид
II  ((dx1 )2  (dx 2 )2 ) . Имеет
место следующая
Лемма 1. Пусть
(m  1) -связная
поверхность
F2
положительной внешней кривизны
K  k0  0 , k0  const , в римановом пространстве R 3 , удовлетворяющая условиям регулярности, подвергнута бесконечно малой ARG -деформации с заданным коэффициентом рекур
i 

рентности  и с полем смещения z  a y,i cn . Тогда уравнение для функции c в координатной форме имеет вид:
2
g
 ( 
i 1
При этом функции
i
i c)  (1   )2 H gc  0 .
a i , находятся по формуле ai  
ic
.

ARG K  k0  0 ,
Доказательство. Известно из [1], что уравнение для функции с, возникающее при
деформации поверхности
k0  const ,
имеет вид:
gij  a y,i y,j , b ij
тичной
F
формы
~
a i  b ij  j c .
2
 , при условии
 k ( gb ik ic)  (1   )2H gc  0 , где g  det gij
с коэффициентом рекуррентности
– матрица, обратная к матрице
поверхности,
ic 
c
.
x i
bij
Координаты
,
коэффициентов второй квадра-
ai
находятся
из
выражения
Так как на поверхности введена изотермически-сопряженная параметризация, то есть
  (dx1  dx 2 ) , то b11  b22   , b12  0 , при этом b11  b 22 
1 12
, b  0 , где

13
Вестник ТГПИ
Естественные науки
( x1 , x 2 )  D . Тогда уравнение для функции c , описывающее ARG -деформацию поверхно2
сти F с коэффициентом рекуррентности  , в этих координатах примет вид:
2
g
i (
i c)  (1   )2 H gc  0 , ( x1 , x 2 )  D , где c – искомая функция.


i 1
ic
i
i
При этом функции a находятся по формуле a  
. Лемма доказана.

П.3. Дадим аналитическую запись условия обобщенной втулочной связи. Отметим, что при

изотермически-сопряженной параметризации тангенциальная составляющая l поля
 {l1 , l2 } на границе D
в поле векторов l
Лемма 2. Пусть на краю
F 2
области
поверхности
D
F2
в плоскости
l
( x1 , x 2 ) . Имеет место
задано векторное поле (2). Пусть, далее,
F 2
2
поверхность F при бесконечно малой ARG -деформации подчинена вдоль края
вию обобщенной втулочной связи (3). Тогда это условие можно представить в виде:
c
 l 3c  h í à D ,
l
 l
l2 
1
по направлению l  
,

2
2
2
2
 l1  l2 l1  l2 
l12  l22
где
c
l
– производная
переходит
усло-
(4)
в плоскости
( x1 , x 2 ) ,
li  gijl j .
Доказательство. Так как координаты векторного поля смещения



z  a y,i cn
i
, а координаты
l

имеют вид:


3 
l  l y,i l n
i
z
имеют вид:
, то
a z  l   a (a i y ,i  cn )(l j y , j l 3n  ) 
 a y ,i y , j a il j  a y , j n cl j  a y ,i n  a il 3  a n n  cl 3 
1
 c    c 
 g ij a il j  cl 3  a ili  cl 3    1 l1     2 l2   cl 3   (1c  l1   2c  l2 )  cl 3 ,

     
Подставим последнее равенство в (3) и получим
1c  l1   2c  l2  cl 3  h .
Умножим (5) на
где
1
l12  l22
и получим
c
l 3c
h


l
l12  l22
l12  l22
c
l1
l2
 1c 
  2c 
l
l12  l22
l12  l22
плоскости
( x1 , x 2 ) .
Умножим
– производная по направлению
последнее
равенство
мах 1 и 2, сводится к изучению разрешимости краевой задачи
14
на
,
 l
l2 
1
 2 2, 2 2в
 l1  l2 l1  l2 
l12  l22
и
получим
c
 l 3c  h , что совпадает с (4). Лемма доказана.
l
2
П.4. Нахождение бесконечно малых ARG -деформаций поверхности F с полем смещеz  ai y,i cn при условии обобщенной втулочной связи (3), как было показано в лем-
l12  l22
ния
(5)
Раздел I.
Алгебра и геометрия
 2
g
 i c)  (1   )2 H gc  0 вâ D,
  i (
 i 1

\

 l 2  l 2 c  l 3c  h
на
í à D,
1
2

l

где
(6)
g  C 2, ,   C1, , H  C1, , l  C1, , l 3  C1, , 0    1 .
ic
i
i
При этом функции a находятся по формуле a  
.

Так как внешняя кривизна поверхности положительна K  k0  0 , k0  const ,
h  h ;
то
дифференциальное уравнение задачи (6) является эллиптическим. В силу ориентации поверхности
0
и поэтому
g
0.

По условию теоремы коэффициент рекуррентности
  1
и
H  0 , поэтому для уравнения задачи (6) имеем (1   )2H g  0 . Так как тангенциальная

составляющая l поля
сти

l
образует тупой угол с тангенциальной нормалью
F 2 , то при изотермически-сопряженной параметризации прообраз l
вектора

образуют тупой угол в плоскости

края поверхно
вектора l и прообраз
( x1 , x 2 ) . Следовательно, вектор l
образует
D . Поэтому краевая задача (6) является третьей кра3
3
евой задачей. По условию теоремы функция l  0 , поэтому имеем l  0 . В силу сказан1,
ного, задача (6) для любой заданной функции h класса C , 0    1 , имеет единственное
2,
решение c класса C , 0    1 . Это решение можно представить в виде
c( x1 , x 2 )   F ( x1 , x 2 , y1 , y 2 )h ( y1 , y 2 )d y , где F – функция Грина рассматриваемой
острый угол с внешней нормалью к области
D
задачи. При этом справедлива оценка:
c
где
C 2, ( D )
P h
C1, ( D )
,
(7)
P  const .
По известной функции
c
однозначно восстанавливается поле смещения
заданной обобщенной втулочной связью поверхности
щения
z
F2
вдоль края
z , совместимое с
F 2 . При этом поле сме-
C 1, , 0    1 , в области D , причем его нормальная соcn принадлежит классу C 2, , 0    1 .
является полем класса
ставляющая
Покажем, что при сделанных предположениях данная связь является корректной. Для этого
h в классе C 1, , 0    1 , соответz в классе C 1, , 0    1 .
необходимо убедиться, что малому изменению величины
ствует малое изменение поля смещения
Запишем задачу (6) в операторном виде:
 Lc  0

 Bc  h
2
где
L   i (
i 1
вâ D,
\
на
í à D,
(8)
g

 i )  (1   )2 H g , B  l12  l22  l 3 .
l

15
Вестник ТГПИ
Естественные науки
Пусть имеем два значения величины
при
h  h1
через
h : h  h1 , h  h2 . Обозначив решение задачи (8)
c1 , а при h  h2 через c2 , получим
 Lc1  0 вâ D,

на
 Bc1  h1 í à D.
 Lc2  0 вâ D,

на
 Bc2  h2 í à D.
Тогда, вычитая из первой полученной задачи вторую, находим:
 L(c1  c2 )  0

 B(c1  c2 )  h1  h2
в â D,
на
í à D.
В силу оценки (7), для задачи (9) имеем
(9)
c1  c2
C 2, ( D )
 P h1  h2
C1, ( D )
.

 z2  (a11  a12 ) y1  (a12  a22 ) y2  (c1  c2 )n 
1
1
  (1c1  1c2 ) y1  ( 2c1   2c2 ) y2  (c1  c2 )n 


1
1
  1 (c1  c2 ) y1   2 (c1  c2 ) y2  (c1  c2 )n , где zi – векторное поле,


соответствующее решению задачи (8) при h  hi .
Далее, имеем z1
1 (c1  c2 ) C1, ( D )  c1  c2
Так как
то
z1  z2
1,
C
( D)

1
c1  c2

C
2,

( D)
C 2, v ( D )
,
 2 (c1  c2 )
1
c1  c2

C 2, ( D )
C1, ( D )
 c1  c2
 c1  c2
C 2, ( D )
C 2, ( D )
,
.
2
P
c1  c2 C 2, ( D )  (2  ) h1  h2 C1, ( D ) .
C ( D)


Таким образом, малому изменению величины h соответствует малое изменение поля сме1,

щения z в классе C , 0    1 . Следовательно, обобщенная втулочная связь (3) является
1,
корректной в классе C , 0    1 , в отношении бесконечно малых ARG -деформаций с
коэффициентом рекуррентности  ,   1 . Теорема доказана.
Следовательно,
z1  z2
1,

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Fomenko V.T. ARG -deformations hypersurface with boundary in Riemannial space. Tensor, N.S. vol. 54
(1993). Chigasaki, Japan.
2. Векуа И.Н. Обобщенные аналитические функции/ под ред. О.А. Олейник и Б.В. Шабата.2-е изд., перераб. М.: Наука / гл. ред. Физмат. Лит., 1988. 512с. ISBN 5-02-013747-2.
В.Т. Фоменко
ВЫЧИСЛИТЕЛЬНАЯ ГЕОМЕТРИЯ
Вычислительная геометрия как раздел математики сформировался в последние четыре десятилетия благодаря бурному развитию электронной вычислительной техники. Термин "вычислительная геометрия", ставший в настоящее время общепринятым, ввел в 1971 г. английский математик А.Р. Форрест, который определил вычислительную геометрию как представление в ЭВМ,
анализ и синтез информации о геометрическом образе [1]. Основными геометрическими образами в
вычислительной геометрии являются кривые и поверхности на плоскости и в пространстве. До последнего времени проектирование кривых и поверхностей для нужд промышленности, как правило,
осуществлялось графическим способом с помощью различных приемов, разработанных в начерта16
Раздел I.
Алгебра и геометрия
тельной геометрии, и являлось трудоемкой работой. Новые методы проектирования, составляющие
содержание вычислительной геометрии, основаны на использовании аналитического аппарата, в
частности, привлечении сплайн-функций, алгебраических кривых, конических сечений ([2]-[5]). Эти
методы требуют замены чертежных работ большим объемом вычислений на ЭВМ, что приводит к
созданию различных автоматизированных систем проектирования поверхностей, широко используемых для работы на станках с числовым программным управлением.
Естественно, что математическое представление исследуемого объекта проводится в цифровых данных и сохраняется в памяти ЭВМ. Это дает возможность избежать неточностей проектирования, связанных с плазовым методом, и легко проводить вычисления геометрических характеристик, необходимых для описания объекта. Однако главное преимущество методов вычислительной
геометрии заключается в возможности вести процесс проектирования с анализом полученного результата и введения необходимой корректировки проектирования до получения готового изделия.
Поясним это на примере, который будет изложен более подробно ниже. Допустим, что требуется
построить непрерывно дифференцируемую кривую, проходящую через точки заданного плоского
набора точек. Существуют различные способы построения таких кривых. Наиболее распространенными являются методы интерполирования многочленами, например, многочленом Лагранжа.
Последний содержит много осцилляций, и потому, как правило, требуются некоторые изменения
многочлена на каком-то участке. Однако, изменения многочлена Лагранжа на некотором участке
влечет изменение этого многочлена на всем наборе точек, что приводит к ликвидации всех ранее
полученных вычислений.
Методы вычислительной геометрии, разработанные Форрестом, Фергюссоном и Кунсом для
проектирования кривых и поверхностей являются наглядно геометрическими и базируются на разделах классической аналитической и дифференциальной геометрии, векторной и элементарной матричной алгебры. В рассматриваемом случае проектировщик определяет некоторую незамкнутую ломанную кривую для заданного набора точек и выносит ее изображение на дисплей, после чего система автоматического проектирования аппроксимирует эту ломанную гладкой кривой, также выносимой на дисплей. Внеся различные изменения в исходную ломанную на некоторых участках,
проектировщик может изменить на этих участках аппроксимирующую кривую, оставляя ее неизменной на остальных участках набора. Важно отметить, что непрерывное изменение ломанной влечет за собой непрерывное изменение на соответствующем участке аппроксимирующей кривой в рассматриваемом классе регулярности.
Таким образом, разработанная система реализует диалоговый режим обмена информацией
между проектировщиком и ЭВМ. Подобным образом можно проектировать и поверхности. Для
этого предварительно строится незамкнутая многогранная поверхность, соответствующая заданному пространственному набору точек, и для нее находится гладкая аппроксимирующая поверхность. Более того, метод Кунса, описанный ниже, делает возможным построить гладкую поверхность, натянутую на систему двух пересекающихся семейств гладких кривых.
1. ГЛАДКАЯ АППРОКСИМАЦИЯ ПЛОСКИХ ТОЧЕЧНЫХ МАССИВОВ
КРИВЫМИ ВТОРОГО ПОРЯДКА
Пусть на плоскости с декартовой прямоугольной системой координат Оху задан упорядоченный
набор
Множество
точек
своими координатами
.
будем называть плоским точечным массивом. Будем решать задачу аппроксима-
17
Вестник ТГПИ
Естественные науки
ции данного плоского точечного массива с заданной точностью
. Решение этой задачи бу-
дем искать в классе кривых с непрерывно изменяющейся касательной и состоящей из дуг кривых
второго порядка. Необходимо также договориться, что следует понимать под точностью аппроксимации. Обычно это делается следующим образом. Пусть
аппроксимирующей точечный массив
– уравнение кривой
. Из курса дифференциальной геометрии известно, что
при подстановке координат точки
в выражение
и нормировке результата
получается величина
,
эквивалентная величине
что отношение
,
– расстоянию точки
от рассматриваемой кривой
стремится к единице, когда точка
. Это означает,
неограниченно приближается к кри-
вой , оставаясь вне кривой. Если точка Mi находится достаточно близко к кривой
ее от кривой можно приближенно вычислять по формуле
, то расстояние
. В случае, когда рассматри-
ваемая кривая является прямой на плоскости, полученная приближенная формула для вычисления
превращается в точную.
В связи с этим говорят, что кривая
аппроксимирует точечный массив
с заданной точностью, если выполнено условие
.
Задача аппроксимации плоского точечного массива с заданной точностью имеет много решений, даже, если эту задачу решать в классе гладких кривых, состоящих из дуг кривых второго порядка. Простейшее решение можно получить, например, составив аппроксимирующую кривую
из дуг окружностей, проходящих через каждые две соседние точки с условием гладкого сопряжения
на концах. Однако, такая кривая не всегда может удовлетворить требованиям проектировщика.
Обычно поставленную задачу решают при некоторых дополнительных условиях. Говорят, что
плоский точечный массив
является выпуклым, если ломаная
, соеди-
няющая последовательно точки массива, является выпуклой ломаной. Разбивая данный массив, если это необходимо, на выпуклые массивы, будем решать задачу аппроксимации для выпуклого
массива точек. Сопрягая гладким образом полученные кривые на выпуклых участках, получим аппроксимирующую гладкую кривую для всего данного массива точек.
Пусть
ные
– концы выпуклого массива точек
, к аппроксимирующей кривой
. Зададим в точках
, выбрав их, например, касательными к окружностям,
проходящим, соответственно, через точки
Будем считать, что касательные
касатель-
и
пересекаются в точке
.
, а точечный массив
лежит внутри треугольника
. Искомую аппроксимирующую кривую
отыскивают, следуя
Р.А. Лаймингу, среди пучка
кривых второго порядка, заданного уравнением:
,
где
ственно;
, – уравнения прямых
– числовой параметр. При
и
соответственно, пару пересекающихся прямых
18
кривые пучка
соответпредставляют собой,
и пару совпавших прямых
. Поэтому
Раздел I.
Алгебра и геометрия
в дальнейшем можно считать, что
ках
точке
для любого значения
. Дуга кривой
. В самом деле, по определению прямая
, если пересечение прямой
и кривой
и кривой
в точ-
касается кривой
представляет собой точку
как пару совпавших точек. Найдем точки пересечения прямой
сительно
касается прямых
в
рассматриваемую
. Для этого решим отно-
совместно систему уравнений:
.
Преобразуем эту систему к виду:
.
Эта система для любого
наты точки
имеет точно два совпавших решения, дающих коорди-
. Отсюда следует, что прямая
бого отличного от нуля значения
в точке
. Кривая
в точке
. Аналогично устанавливается, что кривая
пучка
минимум значения функции
является касательной к кривой
для лю-
касается кривой
, дающая наилучшее приближение точечного массива, дает
по параметру
удовлетворяет уравнению
, и потому соответствующее значение параметра
. Если при найденном из этого уравнения значении параметра
соответствующая кривая пучка не обеспечивает требуемую точность аппроксимации, точечный массив разбивают на два, и процесс аппроксимации продолжается на вновь полученных массивах.
Описанный выше алгоритм нахождения аппроксимирующей кривой целесообразно применять в тех случаях, когда исходный точечный массив требуется дополнить новыми точками, равномерно распределенными по кривой.
2. РАЦИОНАЛЬНАЯ ПАРАМЕТРИЗАЦИЯ КРИВОЙ
ВТОРОГО ПОРЯДКА
Рассмотрим на плоскости гладкую дугу
чим через
кривой второго порядка с концами
точку пересечения касательных
параметрическое уравнение дуги
к кривой
в точках
, считая заданными радиус-векторы
. Обозна-
. Выведем векторное
точек
соответственно (рис. 1).
Пусть М – текущая точка кривой
с радиус-вектором .
Положим
,
где
(1)
– некоторые числа, определяющие положение точки
с базисом
разованного прямыми
. В аффинных координатах
и началом в точке Р уравнение пучка кривых второго порядка, обимеет вид:
, где
Уравнение касательной к кривой
в точке
– числовой параметр.
имеет вид:
.
19
Вестник ТГПИ
Естественные науки
Полагая сначала
, а затем
, и учитывая, что
, находим отсюда значения координат точек
:
;
.
Обозначим:
тогда находим
,
.
;
Отсюда следует, что
.
Так как
.
Это означает, что
Выражая
.
через
, получим:
. Подставляя найденные значения
находим радиус-вектор точки
в формулу (1),
:
.
(1)
Вводя в это выражение параметр , окончательно находим искомое уравнение кривой в виде:
,
где
(2)
.
Это уравнение называют рациональным квадратичным векторно-параметрическим уравнени-
ем кривой
точке
тельных
. Геометрический смысл коэффициента
кривой
, наиболее удаленной от хорды
в уравнении (2) заключается в том, что в
, касательная к кривой
точками в отношении
дуга
. Это означает, что при
есть, соответственно, кусок гиперболы, параболы и эллипса.
Непосредственный подсчет показывает, что кривизна кривой
в точках
формуле
,
,
где квадратные скобки обозначают векторное произведение векторов.
20
делит отрезки каса-
вычисляется по
Раздел I.
Алгебра и геометрия
Данный плоский массив точек
можно интерполировать кривой
с непрерывной
кривизной и состоящей из дуг кривых второго порядка следующим образом. Зададим в каждой точке массива касательную к кривой
и значения кривизны в точке
. Тогда по описанному
выше способу находим однозначно кривую второго порядка, идущую из точки
заданными касательными и заданной кривизной в точке
точке
в точку
с
. Вычисляя для нее кривизну в соседней
, мы получаем исходные данные для нахождения кривой на следующем этапе интерполя-
ции. Составная кривая будет интерполяционной кривой с непрерывной кривизной.
3. КУБИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КРИВЫЕ
В ФОРМЕ ФЕРГЮССОНА И БЕЗЬЕ
В 1963 г. Д.С. Фергюссон предложил отыскивать уравнение кривой
ки
с заданными касательными
, проходящей через точ-
в этих точках, в виде:
,
где
– параметр,
точки
(3)
– некоторые постоянные векторы. Так как
и касательные
где
знак
считаются заданными, то, выражая
означает
производную
по
через
параметру
находим:
(4)
Векторы
можно представить в виде
,
где
и
Числа
– единичные касательные векторы к кривой
в точках
соответственно.
называются весовыми величинами. Их можно подбирать, исходя из требуемого
вида кривой
. Зависимость формы кривой
, заданной уравнением (4) от параметров
показана на рис. 2. Кроме того, величины
визна кривой
можно выбирать таким образом, чтобы кри-
достигала заданного значения на концах
.
В 1970 г. П. Безье предложил другую форму записи уравнения (3), сделав наглядным смысл
входящих в него векторных величин. Формула П. Безье имеет вид:
(5)
где
; радиус – векторы некоторых заданных точек
.
Из формулы (5) следует, что кривая, заданная в форме Безье, проходит через точки
в
этих
точках
касательные,
имеющие,
(рис. 3). Прямые
соответственно,
направление
имеет
векторов
образуют фигуру, называемую ха-
рактеристической ломаной заданной кривой. Чтобы построить кривую
, мы задаем точки
,
21
Вестник ТГПИ
Естественные науки
касательные к кривой в этих точках, и на касательных выбираем точки
точек
мы меняем форму кривой
. Изменяя положение
, которая в некоторой степени повторяет форму характери-
стической ломаной (рис. 3).
Формулы Фергюссона и Безье удобно использовать для сопряжения участков кривых при
интерполировании кривыми с непрерывной кривизной точечных массивов, содержащих точки перегиба. Возможны и другие формы записи полиномиальных кривых, обобщающие уравнение (5).
4. ПОВЕРХНОСТИ В ФОРМЕ КУНСА И ФЕРГЮССОНА
Проектирование поверхности начинается с построения на ней криволинейной сети, содержащей основную информацию о поверхности. Как правило, линии такой сети берут в качестве координатных линий на поверхности (например, продольные (ватерлинии) и поперечные (шпангоуты)
сечения судна; параллели и меридианы поверхности вращения и т.д.). Сеть на поверхности, образованную линиями выбранных семейств, будем называть каркасом поверхности. Каркас поверхности
разбивает последнюю на криволинейные прямоугольники, называемые ячейками поверхности.
Каждая из ячеек является элементом проектирования поверхности. Задача проектировщика заключается в построении поверхности, проходящей через заданный каркас и удовлетворяющей заданным требованиям гладкости, выпуклости, искривленности и т.д.
Ниже описывается предложенный Кунсом и развитый Фергюссоном метод построения гладкой поверхности, натянутой на заданный каркас.
Решим, прежде всего, задачу построения ячейки поверхности
, проходящей через заданные
кривые:
.
Аппроксимируем искомую поверхность следующими линейчатыми поверхностями:
где
.
Уравнения
и
изображают отрезки прямых, соединяющих точки
,
соответственно (рис. 4).
Проверим, что поверхность
, заданная уравнением
изображает поверхность, проходящую
через каркас, образованный кривыми
22
. В самом деле, полагая,
, находим
Раздел I.
Алгебра и геометрия
Это означает, что кривая
лежат на
, лежит на поверхности
. Аналогично убеждаемся, что
. Эта конструкция, использующая только информацию о границе поверхно-
сти, определяет наиболее простой класс поверхностей и предложена в 1967 г. Кунсом. Данная
здесь трактовка принадлежит Форресту (1972 г.).
Уравнение ячейки поверхности Кунса можно записать в матричном виде:
(6)
где функции
называют функциями смешивания.
Имея сетку кривых, образующих каркас поверхности, можно сконструировать составную поверхность из ячеек описанного вида (6). Эта поверхность будет непрерывной, но, вообще говоря, не
гладкой. Непрерывность изменения касательной плоскости вдоль составной поверхности
обеспе-
чивается более сложным уравнением ячейки, что достигается другим выбором функций смешивания и
заданием наклона касательных плоскостей к поверхности вдоль кривых каркаса с помощью векторов
. Для получения уравнения такой поверхности
составляем, как и ранее, уравнения поверхностей
, интерполирующих ячейку поверхности
F, в виде:
,
где индекс
означает транспонирование матрицы,
–
функции смешивания, удовлетворяющие условиям:
(7)
матрица
имеет вид:
.
23
Вестник ТГПИ
Естественные науки
Отметим, что в матрицу
входят также значения смешанной производной в вершинах
ячейки, которые можно задать заранее.
Уравнение искомой ячейки поверхности
, натянутой на заданный каркас и имеющей за-
данные направления нормали к поверхности вдоль граничных кривых ячейки, задается формулой
. Используя это уравнение ячейки поверхности, можно построить из нескольких ячеек поверхность с непрерывным изменением касательной плоскости вдоль всей поверхности.
Простейшие функции смешивания, удовлетворяющие условиям (7), были указаны
Фергюссоном:
В заключение отметим, что внешне геометрические свойства поверхностей Фергюссона,
натянутых на заданный каркас, наглядно просматриваются для случая, когда заданный каркас образован семейством кривых
, получаемым из двух плоских кривых
путем парал-
лельного перемещения одной кривой по другой. Такой каркас можно назвать каркасом переноса.
Имеет место следующий результат, установленный автором: поверхность в форме Фергюссона,
натянутая на каркас переноса, является поверхностью переноса. Другими словами, поверхность
Фергюссона может быть получена в пространстве путем трансляции кривой
Рис. 1
Сегмент конического сечения с заданными касательными на концах
24
по кривой
.
Раздел I.
Алгебра и геометрия
Рис. 2
Зависимость формы кубической кривой
25
Вестник ТГПИ
Естественные науки
Рис. 3
Зависимость формы кривой Безье от формы характеристической ломаной
Рис. 4
Аппроксимация ячейки поверхности линейчатыми поверхностями
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Forrest A.R. Computational Geometry. Proc. Roy. Soc. Lond, 1971. С. 187–195.
2. Фокс А., Пратт М. Вычислительная геометрия. М.: Мир, 1982. С. 302.
3. Стародетко Е.А. Элементы вычислительной геометрии. Минск: Наука и техника, 1986. С. 240.
4. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. М.: Наука, 1980. С. 352.
5. Стечкин С.Б., Субботин Ю.Н. Сплайны в вычислительной математике. М.: Наука; 1976. С. 248.
В.Т. Фоменко, О.Н. Фартушная, В.В. Сидорякина
ОБ ОДНОМ ОБОБЩЕНИИ ТОРА КЛИФФОРДА В
П.1 Известно, что тор Клиффорда
окружностей
1
a
и
1
b
4
определяется как произведение двух
радиусов a и b, соответственно. Тор Клиффорда обладает рядом заме-
чательных свойств, в частности:
26
в
Раздел I.
Алгебра и геометрия
1) имеет плоскую метрику;
2) имеет плоскую нормальную связность;
3) имеет нулевое нормальное кручение в любой точке по любому направлению;
4) имеет постоянные главные кривизны, равные, соответственно,
5) имеет постоянную среднюю кривизну
;
;
2
6) индикатриса кривизны тора Клиффорда есть отрезок прямой длины
7) тор Клиффорда
2
) радиуса
лежит на гиперсфере
8) индикатриса кривизны в оснащении
В(0,
;
;
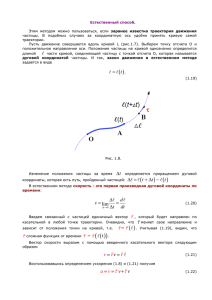
3 имеет вид, изображенный на рисунке:
1
)
b
P
H
M
A(
1
,0)
a
4
Перечисленными свойствами тор Клиффорда с точностью до движения в
определен. Это означает, что задав поверхность
некоторые
действительные
числа,
можно
в
4
утверждать,
однозначно
с указанными свойствами, где a и b –
что
2
есть
тор
Клиффорда
1
b
П.2. Определение. Обобщенным тором Клиффорда в
4
назовем поверхность
2
, обла-
дающую следующими свойствами:
1) поверхность
2) поверхность
2
2
имеет плоскую метрику,
имеет плоскую нормальную связность.
Докажем следующую теорему:
27
Вестник ТГПИ
Естественные науки
Теорема 1. Обобщенный тор Клиффорда в
)и
), где
1
и
2
4
есть произведение двух плоских кривых
)и
– кривизны кривых
), соответственно.
Доказательство. Так как поверхность имеет нулевую кривизну, то на поверхности
)
ввести декартовы координаты
так, что метрика
Так как нормальная связность поверхности
2
2
2
можно
2
имеет вид:
.
является плоской, то, не нарушая в общности,
можно считать, что нормальное оснащение, порожденное ортонормированным базисом
3,
таково, что вторые квадратичные формы поверхности
2
имеет вид:
;
.
В самом деле, индикатриса кривизны есть отрезок прямой (в силу плоской нормальной
связности) и этот отрезок просматривается из точки поверхности под прямым углом (в силу плоской метрики точка поверхности лежит на ортооптической окружности).
Обратимся к уравнениям Кодацци:
Отсюда находим
Эти уравнения дают:
0.
Так как
, то имеем
Обратимся к уравнению Риччи. Имеем
28
Раздел I.
Алгебра и геометрия
оно выполняется тождественно.
Далее находим:
2
Покажем, что в этом случае
есть произведение двух кривых
),
). Полагаем:
где
.
}
Далее положим
};
};
}
}
2
0. Это означает, что основные формы поверхностей
Следовательно, поверхности
2
и
2
совпадают.
4
отличаются друг от друга на движение в
.
П.3. Докажем теперь обратную теорему:
),
Теорема 2. Пусть
кривые с кривизной k
2
i, i=1,2 Тогда поверхность
2
где
– есть плоские
есть обобщенный тор Клиффорда.
Доказательство.
Положим
},
}и
метры кривых
где
y
– натуральные пара-
}. Под-
счет показывает:
};
29
Вестник ТГПИ
Естественные науки
};
;
)
;
)
0.
2
Это означает, что метрика поверхности
ность поверхности
2
имеет нулевую кривизну, и нормальная связ-
), есть
является плоской, то есть поверхность
обобщенный тор Клиффорда, что и доказывает теорему 2.
П.4. Ранее в работах [1], [2] изучались бесконечно малые ARG – деформации тора Клиф4
форда и его кусков в
2
ного тора Клиффорда
. Здесь будут изучены бесконечно-малые ARG – деформации обобщенлибо его односвязных кусков в
4
. Далее будем считать, что парамет-
) пробегают некоторую односвязную область D числовой плоскости
ры
2.
В случае, ес-
ли обобщенный тор Клиффорда представляет собой замкнутую без границы ограниченную по-
0, то будем изучать ARG – деформации универсальной накрывающей тора
верхность рода
2
.
), где z
Положим
что
, где
0и
вектор средней кривизны поверхности,
ности,
R;

2
таково,
 – элемент площади поверхности, H –
 – заданный действительный коэффициент реккурент-
– единичный бивектор нормальной плоскости для
Уравнение ARG – деформации поверхности
30
– поле деформации поверхности
2
имеют вид:
2
.
Раздел I.
Алгебра и геометрия
Полагая
носительно
где
, отсюда находим систему дифференциальных уравнений от
. Имеем

,
– вектор средней кривизны,
.
Для поверхности
2
эта система принимает вид:
Отсюда следует, что
0
Последнее соотношение перепишем в виде
.
Так как левая часть этого уравнения зависит от x, а правая от y, то последнее уравнение эквивалентно двум уравнениям:
/
)
31
Вестник ТГПИ
Естественные науки
Будем считать, что в некоторой точке
0
поверхности
2
наложена внешняя связь
) имеем:
0. Это означает, что в точке
.
Отсюда следует, что функции  и  удовлетворяют начальным условиям:
)
Задача
),
) всегда имеет единственное решение
любой заданной постоянной
0
y) для
и любом значении  Таким образом, доказана
2
Теорема 3. Любая поверхность
(или её часть) при закрепленной точке
допускает
0
однопараметрическое семейство ARG – деформации для любого фиксированного коэффициента
рекуррентности .
Замечание. Положим
. Тогда имеем:
Это означает, что поверхность
допускает ARG – деформации, зависящие от 5 парамет-
), то
ров. Если закрепить точку
Так как
2
0 и потому
0, то
Это означает, что при закрепленной точке
0 при условии, что
и
1 поверхность
раметрическое семейство ARG – деформации с параметром
также в теореме 3.
32
0
0.
0,
2
0.
допускает однопа-
. Это утверждение содержится
Раздел I.
Алгебра и геометрия
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
4
1. Фоменко В.Т. Бесконечно малые ARG – деформации тора Клиффорда в Е . Вестник ТГПИ; Естественные науки, 2007. № 1. С. 21-33.
4
2. Бабенко О.Н. Бесконечно малые ARG-деформации куска тора Клиффорда в Е . Вестник ТГПИ; Естественные науки, 2008. № 1. С. 21-26.
33