На рисунке изображена прямая l , которая является

Самостоятельная работа № 1.
Задачи с практическим содержанием.
Вариант 1.
1. Почтовая марка стоит 6 руб. 50 копеек. Какое наибольшее число этих марок можно
купить на 70 рублей?
2. В городе живёт 240000 жителей, среди них 30% детей и подростков. Среди
взрослых 25% не работают (пенсионеры, домохозяйки, безработные). Сколько
взрослых работают?
3.На заводе, выпускающем DVD-приводы для персональных компьютеров, все
изготовленные за рабочую смену приводы нумеруют и укладывают в коробки по 8
штук в каждой. В какую по счету коробку попадет DVD - привод под номером 222?
4.Семья из трёх человек едет из Челябинска в Волгоград. Можно ехать или поездом,
или на своей машине. Билет на поезд стоит 2150 руб. на одного человека. Автомобиль
расходует 13 литров бензина на 100км пути. Расстояние по шоссе равно 1690 км, а
цена бензина равна 30 руб. за литр. Во сколько рублей обойдется самая дешёвая
поездка.
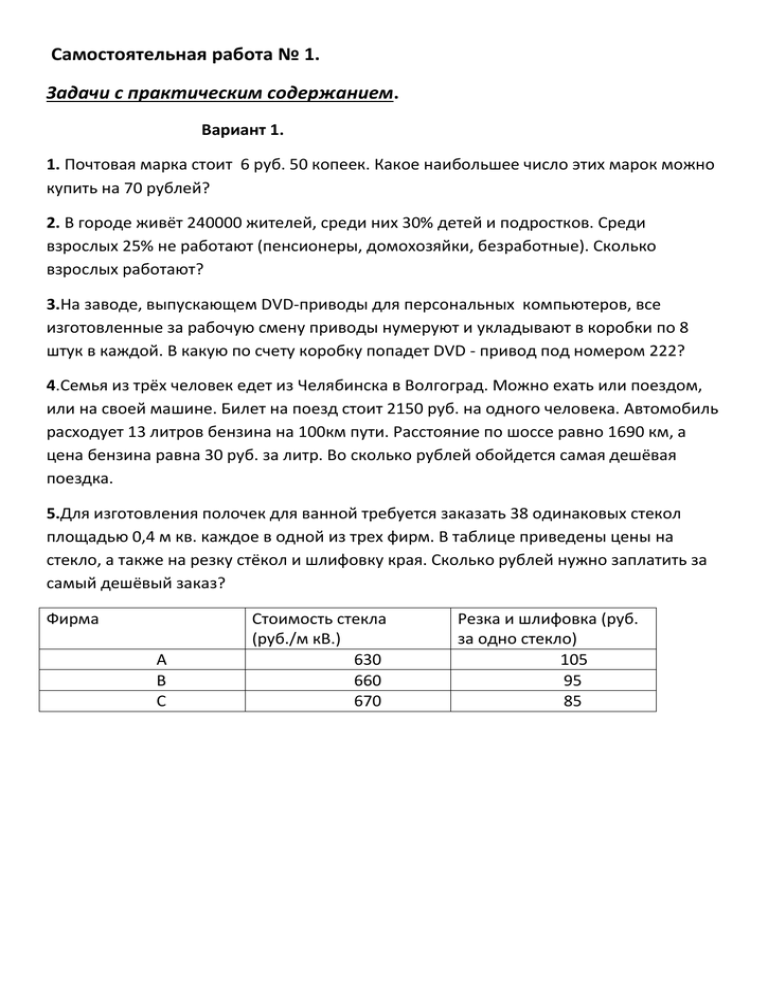
5.Для изготовления полочек для ванной требуется заказать 38 одинаковых стекол
площадью 0,4 м кв. каждое в одной из трех фирм. В таблице приведены цены на
стекло, а также на резку стёкол и шлифовку края. Сколько рублей нужно заплатить за
самый дешёвый заказ?
Фирма
А
В
С
Стоимость стекла
(руб./м кВ.)
630
660
670
Резка и шлифовка (руб.
за одно стекло)
105
95
85
Вариант 2.
1. Один метр ткани стоит 420 рублей. Какое наибольшее целое число метров ткани
можно купить на 16000 рублей?
2. В доме 300 квартир, из которых 55% однокомнатные. Среди многокомнатных
квартир этого дома 80% квартир двухкомнатные. Сколько квартир этого дома не
менее чем трёхкомнатные?
3. На швейной фабрике, изготавливающей постельное бельё, все сшитые за рабочую
смену комплекты постельного белья нумеруют и укладывают в коробки пo 7 штук в
каждой. В какую по счёту коробку попадет комплект под номером 321 ?
4. Семья из четырёх человек едет из Тынды в Кисловодск. Можно ехать или поездом,
или на своей машине. Билет на поезд стоит 6650руб. на одного человека. Автомобиль
расходует 12 литров бензина на 100км пути. Расстояние по шоссе равно 7620км, a
цена бензина равна 30руб. за литр. Во сколько рублей обойдётся самая дешёвая
поездка?
5. Дли сборки трюмо требуется заказать 15 одинаковых зеркал площадью 0,6м2
каждое у одного из трех поставщиков .В таблице приведены цены на зеркала, а также
на резку зеркал и обработку края. Сколько рублей будет стоить самый дешевый заказ
?
Поставщик
A
B
C
Стоимость зеркала
(руб.за 1м2 )
720
750
800
Резка и обработка (руб.
за одно зеркало)
90
75
70
Вариант 3.
1.В общежитии института в каждой комнате можно поселить четырёх человек. Какое
наименьшее количество комнат необходимо для поселения 217 студентов?
2. В сентябре 1 кг абрикосов стоил 70 рублей, в октябре абрикосы подорожали на 35%,
а в ноябре ещё на 20%. Сколько рублей стоил 1 кг абрикосов после подорожания в
ноябре?
3.В доме, в котором живет Аня, 9 этажей и несколько подъездов. Во всех подъездах
на каждом этаже находится по 5 квартир. Аня живет в квартире №407. Определите
номер подъезда, в котором живет Аня.
4.Для строительства дачи можно использовать один из двух типов фундамента:
бетонный и фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 7
кубометров пеноблоков и 4 мешка цемента. Для бетонного фундамента необходимо
8,5 тонн щебня и 43 мешка цемента. Кубометр пеноблоков стоит 2900 руб., щебень
стоит 800 руб., за тонну, а мешок цемента стоит 400 руб. Сколько рублей придется
заплатить за материал, если выбрать самый дешевый вариант?
5.В таблице даны тарифы на услуги трех служб такси. Предполагается поездка
длительностью 25 минут. Нужно выбрать службу, в которой заказ будет стоить
дешевле всего. Сколько рублей будет стоить этот заказ?
Служба такси
Подача машины
Продолжительность
и стоимость
минимальной
поездки
A
B
C
50 руб.
Бесплатно
40 руб.
Нет
10 мин.-85 руб.
15мин.-110 руб.
Цена 1 минуты
сверх
продолжительности
минимальной
поездки
7 руб.
9 руб.
6 руб.
Если длительность поездки меньше длительности минимальной поездки, указанной в
таблице (для каждой службы – свой временной интервал), то она оплачивается по
стоимости минимальной поездки.
Вариант 4.
1. В оздоровительном лагере 620 детей и 29 воспитателей. Автобус марки «ПАЗ,
школьный» имеет 24 посадочных места. Сколько таких автобусов требуется, чтобы
привезти всех детей и всех воспитателей из лагеря в город за один рейс?
2. В мае 1 кг клубники стоил 150 рублей, в июне клубника подешевела на 20%, а в
июле ещё на 25%. Сколько рублей стоил 1 кг клубники после удешевления в июле?
3.В доме, в котором живет Даша, 5 этажей и несколько подъездов. Во всех подъездах
на каждом этаже находится по 4 квартиры. Даша живет в квартире №70. Определите
этаж, на котором живет Даша.
4.Для строительства дачи можно использовать один из двух типов фундамента:
бетонный и фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 8
кубометров пеноблоков и 6 мешков цемента. Для бетонного фундамента необходимо
10 тонн щебня и 35 мешков цемента. Кубометр пеноблоков стоит 2400 руб., щебень
стоит 850 руб. за тонну, а мешок цемента стоит 350 руб. Сколько рублей придется
заплатить за материал, если выбрать самый дешевый вариант?
5.В таблице даны тарифы на услуги трех служб такси. Предполагается поездка
длительностью 1 час 10 минут. Нужно выбрать службу, в которой заказ будет стоить
дешевле всего. Сколько рублей будет стоить этот заказ?
Служба такси
Подача машины
Продолжительность
и стоимость
минимальной
поездки
A
B
C
Бесплатно
65 руб.
75 руб.
25мин.-200руб.
Нет
20мин.-130 руб.
Цена 1 минуты
сверх
продолжительности
минимальной
поездки
10 руб.
8 руб.
9 руб.
 Если длительность поездки меньше длительности минимальной поездки,
указанной в таблице (для каждой службы – свой временной интервал), то она
оплачивается по стоимости минимальной поездки.
Вариант 5.
1. Больному прописано лекарство, которое нужно пить 4 раза в день по 0,4г в течение
12 дней. В одной упаковке 10 таблеток лекарств по 0,2г. Какого наименьшего
количества упаковок хватит на весь курс лечения?
2.После повышения цены на 5% холодильник стал стоить 26250 рублей. Сколько
рублей стоил холодильник до повышения цены ?
3.В доме, в котором живет Ваня, 16 этажей и несколько подъездов. Во всех подъездах
на каждом этаже находится по 4 квартиры. Ваня живет в квартире №264. Определите
этаж, на котором живет Ваня.
4.Водитель маршрутного такси совершил за месяц 168 поездок по 50 км каждая,
потратив на бензин 29400 рублей. Сколько литров на 100 км расходовал в среднем
водитель, если он покупал бензин по цене 28 руб. за литр?
5.Компания предоставляющая услуги по подключению к сети Интернет, предлагает
следующие тарифные планы:
Тарифный план
“0”
“500”
“700”
Абонентская плата
Плата за трафик
Нет
2,5 р. за 1 Mb
550 р. за 500 Mb в месяц 3,5 р. за 1 Mb сверх 500
Mb
750 р. за 700 Mb в месяц 4 р. за 1 Mb сверх 700
Mb
Клиент компании планирует, что его трафик составит 800 Mb и, исходя из этого,
выбирает наиболее дешевый тарифный план. Сколько рублей заплатит клиент, если
его трафик будет равен 850 Mb?
Вариант 6.
1.В столовой пансионата на каждого отдыхающего полагается 300 мл молока в день.
Какое наименьшее число двухлитровых пакетов молока необходимо приобрести
столовой пансионата на 6 дней, если в пансионате отдыхают 105 человек.
2.Налог на доходы составляет 13% от заработной платы. После вычета налога на
доходы Валерий Иванович получил 23490 рублей. Сколько рублей составляет
заработная плата Валерия Ивановича?
3.В доме, в котором живет Коля, 7 этажей и несколько подъездов. Во всех подъездах
на каждом этаже находится по 3 квартиры. Коля живет в квартире №163. Определите
этаж, на котором живет Коля.
4.Водитель маршрутного такси совершил за месяц 260 поездок по 25 км каждая,
потратив бензин на 23868 рублей. Сколько литров на 100 км расходовал в среднем
водитель, если он покупал бензин по цене 27 рублей за литр?
5. У телефонной компании имеется три тарифных плана – см. таблицу. Абонент
выбрал наиболее дешевый тарифный план, исходя из предположения, что суммарная
длительность телефонных разговоров составит 450 мин в месяц. Какую сумму он
должен заплатить за месяц, если общая длительность разговоров составит 520 мин?
Тарифный план
Абонентская плата
1.
2.
180р. в месяц
300р. за 400 мин. в
месяц
600р. в месяц
3.
Плата за 1 мин.
разговора
0,5 р.
Свыше 400 мин. в месяц
1,5р. за 1 мин.
0 р.
Вариант 7.
1. Во время лечебного курса следует принимать раствор 5 раз в день по 3 мл. В одной
упаковке 6 флаконов раствора по 8 мл. Какое наименьшее количество упаковок
необходимо для лечебного курса длительностью 20 дней?
2. Купив за 100 рублей дисконтную карту, по которой предоставляется 5% скидка, и
воспользовавшись этой картой при покупке принтера, завхоз школы заплатил за
принтер 5320 рублей. Сколько рублей сэкономил на этой покупке завхоз, приобретя
дисконтную карту?
3. Необходимо перевезти 50 одинаковых ящиков весом 450 кг каждый. Сколько
машин грузоподъемностью 3 тонны каждая потребуется для этого?
4. Семья за месяц использовала 8 м. куб. холодной воды и 3 м. куб. горячей воды.
Вычислите сумму (в рублях), которую нужно заплатить семье за пользование
холодной и горячей водой в этом месяце, если холодная вода стоит 10 руб. 80 коп. за
1 м. куб., горячая вода стоит 36 руб. 90 коп. за 1 м. куб., а слив использованной воды10 руб. 30 коп. за 1 м. куб.
5. Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 900 км.
В таблице приведены характеристики трех автомобилей и стоимости аренды. Помимо
аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какова
суммарная стоимость аренды и топлива, если клиент выберет самый дешевый
вариант? Цена дизельного топлива 25 руб. за литр, бензина – 28 руб. за литр, газа -15
руб. за литр.
Автомобиль
Топливо
1.
2.
3.
Дизельное
Бензин
Газ
Расход топлива
на 100км
13
9
15
Арендная плата
за сутки
3200
3600
3800
Вариант 8
1. Двухмесячного щенка немецкой овчарки следует кормить 6 раз в день, давая
каждый раз по 250 граммов корма. В одной упаковке корма 3 пакета весом 700
граммов каждый. Какое наименьшее количество упаковок корма необходимо
приобрести для щенка на 30 дней?
2. Купив за 150 рублей дисконтную карту, по которой предоставляется 7% скидка, и
воспользовавшись этой картой при покупке сканера, Михаил заплатил за сканер 4185
рублей. Сколько рублей сэкономил на этой покупке Михаил, приобретя дисконтную
карту?
3. Необходимо перевезти 50 одинаковых ящиков весом 600 килограмм каждый.
Сколько машин грузоподъемностью 2 тонны каждая потребуется для этого?
4. Семья за месяц использовала 2м куб. холодной воды и 5м куб. горячей воды.
Вычислите сумму (в рублях), которую нужно заплатить семье за пользование
холодной и горячей водой в этом месяце, если холодная вода стоит 11руб.40коп. за
1м куб., горячая вода стоит 63руб.10коп. за 1м куб., а слив использованной воды –
9руб.50коп. за 1м куб.
5. Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 800км.
В таблице приведены характеристики трёх автомобилей и стоимость аренды. Помимо
аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какова
суммарная стоимость аренды и топлива, если клиент выбирает самый дешевый
вариант? Цена дизельного топлива 23руб. за литр, бензина- 26руб. за литр, газ -19руб.
за литр.
Автомобиль
Топливо
1.
2.
3.
Дизельное
Бензин
Газ
Расход топлива
на 100км
12
10
16
Арендная плата
за сутки
4600
4300
4200
Вариант 9
1. В магазине проходит акция: покупая три коробки конфет, четвёртую коробку
покупатель получает в подарок. Какое наибольшее число коробок конфет может
приобрести покупатель на 1900 руб. во время этой акции, если одна коробка конфет
стоит 130руб.?
2. При оплате услуг через платёжный терминал взимается комиссия 3%. Терминал
принимает суммы кратные 10 рублям. Лёша хочет положить на счёт своего
мобильного не меньше 350руб. Какую минимальную сумму он должен положить в
данный момент?
3. Цена газетной бумаги составляет 23900руб. за тонну. Какое наибольшее чисто тонн
газетной бумаги можно купить на 300000руб., если она продаётся рулонами, вес
каждого из которых составляет 400кг?
4. Вася загружает на свой компьютер из Интернета файл размером 19Мб за 28 секунд.
Петя загружает файл размером 54 Мб за 36 секунд, а Коля загружает файл размером
45 Мб за 27 секунд. Сколько секунд будет загружаться файл размером 259 Мб на
компьютере с наибольшей скоростью загрузки?
5. В таблице указаны средние цены (в рублях) на некоторые основные продукты
питания в трёх городах России ( по данным на начало 2010 года).
Наименование
продукта
Пшеничный хлеб
(батон)
Кефир (1л)
Картофель (1кг)
Мясо (говядина)
(1кг)
Подсолнечное
масло (1л)
Иркутск
Вологда
Саранск
19
13
16
39
17
280
36
16
250
32
19
240
70
72
64
Определите, в каком из этих городов окажется самый дешевый следующий набор
продуктов:2 батона пшеничного хлеба, 1,5 кг картофеля, 3кг говядины, 2л
подсолнечного масла. В ответе запишите стоимость данного набора продуктов в этом
городе (в рублях).
Вариант 10
1. В кинотеатре проходит акция: при покупке трёх билетов - четвертый билет в
подарок. Какую наименьшую сумму (в рублях) требуется заплатить во время этой
акции за билеты на группу из 17 человек, если стоимость одного билета составляет
150 рублей?
2. тетрадь стоит 18 рублей. Какое наибольшее число этих тетрадей можно купить на
1500руб., если при покупке более 40 тетрадей предоставляется скидка 4% от
стоимости покупки?
3. Цена картона марки «Gemini» составляет 90300руб. за тонну. Какое наибольшее
число тонн этого картона можно купить за 450000руб., если листы картона упакованы
в пачки массой 150кг каждая?
4. Наташа загружает на свой компьютер из Интернета файл размером 50Мб за 36
секунд. Таня загружает файл размером 52 Мб за 39 секунд, а Люда загружает файл
размером 35 Мб за 21 секунду. Сколько секунд будет загружаться файл размером 300
Мб на компьютере с наибольшей скоростью загрузки?
5. В таблице указаны средние цены (в рублях) на некоторые основные продукты
питания в трёх городах России ( по данным на начало 2010 года).
Наименование
продукта
Пшеничный хлеб
(батон)
Кефир (1л)
Картофель (1кг)
Мясо (говядина)
(1кг)
Подсолнечное
масло (1л)
Краснодар
Псков
Барнаул
15
16
18
32
16
270
36
14
290
38
15
285
61
65
67
Определите, в каком из этих городов окажется самый дешевый следующий набор
продуктов: 2л подсолнечного масла, 7кг картофеля, 1,5л. молока, 2,5кг говядины. В
ответе запишите стоимость данного набора продуктов в этом городе (в рублях).
Образец решения упражнений.
Задания с практическим содержанием.
1. В доме, в котором живёт Ваня, 9 этажей и несколько подъездов. Во всех подъездах
на каждом этаже находится по 4 квартиры. Ваня живёт в квартире №228. Определите
этаж, на котором живёт Ваня.
Решение.
В каждом подъезде 9 · 4 = 36 квартир. Так как 228 = 36 · 6 + 12, то Ваня живёт в
седьмом подъезде, ещё точнее – в 12-ой по счету квартире этого подъезда. А
поскольку 12 = 4 · 3, то Ваня живёт на третьем этаже.
Ответ: 3.
Тетрадь стоит 15 рублей. Какое наибольшее число этих тетрадей можно купить на
1000 руб., если при покупке более 50 тетрадей предоставляется скидка 5% от
стоимости покупки?
Решение.
Пусть 𝑥 – искомое число тетрадей. Заметим, что 𝑥 > 50, так как 1000 > 50 · 15. Поэтому
при покупке 𝑥 тетрадей будет предоставлена 5% скидка и на кассе потребуется
заплатить 0,95 · 15𝑥 рублей. Значит, 𝑥 - это наибольшее целое решение неравенства
0,95 · 15𝑥 < 1000, или неравенства 𝑥 <
1000
. Выражение
0,95 .15
1000
0,95∙15
с точностью до
десятых равно 70,1, поэтому 𝑥 = 70.
Ответ: 70.
2. В одной упаковке 650 компакт-дисков для записи. Завод-изготовитель допускает не
4,7% брака. Какое наименьшее число исправных дисков может быть в упаковке?
Решение.
Так как изготовитель допускает не более 4,7% брака, то число бракованных дисков в
упаковке не превосходит 0,047 · 650 = 30,55. Поэтому наибольшее число бракованных
дисков в одной упаковке равно 30, а наименьшее число исправных дисков равно 650 –
30 = 620.
Ответ: 620.
3. Оптовая цена подсолнечного масла составляет 48300 рублей за тонну. Какое
наибольшее число тонн подсолнечного масла можно купить на 100000 рублей, если
оно продаётся коробками, в каждой из которых 20 бутылок масла по 600 г?
Решение.
Оптовая цена 1 кг масла равна
48300
1000
= 48,3 руб. Так как в одной коробке находится 20
· 0,6 = 12 кг масла, то оптовая цена коробки масла равна
12 · 48,3 = 579,6 руб.
Поэтому наибольшее число коробок масла, которое можно купить на 100000 рублей –
это наибольшее целое число 𝑥, удовлетворяющее неравенству 579,6 · 𝑥 < 100000.
Выражение
100000
579,6
с точностью до десятых равно 172,5, поэтому 𝑥 = 172. В 172
коробках находится 172 · 12 = 2046 кг масла, что составляет 2,064 тонны.
Ответ: 2,046.
4. В салоне парфюмерии проходит акция: покупая флакон духов объёмом 100 мл,
покупатель получает в подарок флакон духов объёмом 30 мл. Какой наибольший
объём (в мл) духов можно получить за 7000 рублей во время этой акции, если флакон
духов объёмом 100 мл стоит 1800 рублей, объёмом 50 мл – 1200 рублей, а объёмом
30 мл – 800 рублей?
Решение.
Так как цена за 1 мл духов наименьшая для флакона объёмом 100 мл, и к тому же при
покупке флакона объёмом 100 мл покупатель получает подарок, то наибольший
объём духов получится при покупке как можно большего числа таких флаконов. Так
как 7000 = 1800 · 3 + 1600, то на 7000 рублей можно купить три флакона объёмом 100
мл и при этом останется 1600 рублей. Чтобы получить как можно больший объём
духов, на оставшиеся 1600 рублей следует купить два флакона объёмом 30 мл. При
этом объём полученных духов будет равен (100 + 30) · 3 + 30 · 2 = 450 мл.
Ответ : 450.
5. Необходимо перевезти 52 одинаковых ящика весом 450 килограмм каждый.
Сколько рейсов понадобится сделать для этого, если использовать машину
грузоподъёмностью 2,5 тонны?
Решение.
Так как 5 · 450 < 2500 < 6 · 450, то на машине грузоподъёмность 2500 кг можно
перевозить до 5 ящиков. А поскольку 52 = 5 · 10 + 2, то для перевозки 52 ящиков
понадобится 11 рейсов такой машины.
Ответ: 11.
ОТВЕТЫ К ЗАДАНИЯМ контрольной работы № 1.
Задания с практическим содержанием.
№ задания
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
1
10
38
55
28
10
95
7
22
18
1950
2
126000
27
113,4
90
25000
27000
180
165
370
86
3
28
46
10
3
2
6
9
17
12,4
4,95
4
6450
26600
21900
20750
12,5
13,6
310,4
404,8
148
180
5
13414
7830
210
625
1350
480
5825
6380
908,5
957
Образец решения упражнений на преобразование выражений.
№1.
6a – 15b + 10 , если
2a  3b
4
=
ab2
3
Решение. Способ 1.
Из равенства
2a  3b
4
= по правилу пропорции имеем:
ab2 3
(2a – 3b ) · 3=4·(a – b + 2), 6a – 9b = 4a – 4b + 8, 2a – 5b = 8. Отсюда получаем : 6a 15b + 10 = 3·(2a – 5b) + 10 = 3·8 +10 =34
Примечание. Заметим , что данное в условии равенство не определяет числа a и
b однозначным образом – подставляя в равенство 2a=5b + 8 вместо b
произвольное число , мы получим пару чисел a и b, для которой данное в
условии равенство выполнено . Но ответ задании не должен зависеть от выбора
числа b . Чтобы ответ в задаче вычислялся однозначно , коэффициенты должны
быть подобраны специальным образом . И это ответственность составителя
задачи , а не ученика! Поэтому при решении подобной задачи на экзамене в
целях экономии времени вполне допустим следующий способ вычисления
правильного ответа .
Способ 2.
Подставляя в равенство
2a  3b
4
= значение b = 0 , получаем:
ab2 3
2a
4
 , 6a = 4(a+2), a = 4 . Подставляя в выражение 6a – 15b + 10 значения a =
a2 3
4 , b = 0, получаем ответ : 6 ·4 + 10= 34 .
Ответ: 34.
№2.
x + 2y – 3z, если 4x + y = 6, 12z – 7y = 20
Решение.
Способ 1.
Если из равенства 4x + y = 6 вычесть равенство 12z – 7y = 20, то получим равенство 4x +
8y – 12z = – 14, левая часть которого отличается от выражения, значение которого
требуется найти, лишь множителем 4.
1
4
Отсюда находим: x + 2y – 3z = · (–14) = –3,5.
Примечание. Так как в условии даны два равенства, связывающие значения трёх
переменных, то значения x ,y, z , не определяются из условия задачи однозначным
образом. Значение любой из переменных x, y, z можно принять равным любому
числу ( после чего две оставшиеся переменные будут определяться однозначно ). Но
ответ не должен зависеть от произвольности выбора значений одной из переменных.
И это опять же ответственность составителя задачи! Поэтому, как и в предыдущем
примере, на экзамене допустимо вычисление ответа по упрощённой схеме.
Способ 2.
Полагая в равенствах 4x + y = 6 и 12z – 7y = 20 число y равным нулю, имеем: 4x = 6,
5
12z = 20, откуда x =1,5 z = , получаем ответ:
3
1,5 – 3 ·
5
= – 3,5
3
Ответ: – 3,5
№3.
5
8 · 15 64
Решение.
5
8 ·
Ответ: 2.
15
1
5
64 = 8 · 64
1
15
  · 2 
= 2
1
3 5
6
6 15
3
5
=2 +
6
15
3
5
2
5
= 2 + =2 .
№4.
30  5 20  30  5 20
Решение.

Заметим, что 30  5 20  25  5  2 5   5  5  и, аналогично, 30  5 20  5  5
2
. Отсюда имеем 30  5 20  30  5 20 
5  5 
2

5  5 
2

2
 5  5  5  5  10
Ответ: 10.
№5.
5
b 2  10 b
b
15
4
, если
b13  16
Решение.
Преобразуем данное в условии выражение следующим образом:
2
5
1
10
b b b

15
4
2
5
b 
1
10

15
4
b

13
4
. Так как b  16, то b
13

13
4
 16

1
4

1
4
16

1
2
Ответ :0,5.
№6.
(√𝟐𝟐)𝒏+𝟑
(√𝟏𝟏)𝒏−𝟏
, если 𝟐𝒏+𝟑 = 𝟗
Решение.
(√22)𝑛+3 √22𝑛−1
=
(√11)𝑛−1 √11
4
∙ (√22) = (√2)𝑛−1 ∙ 222 = √2𝑛−1 ∙ 222 .
Так как 2𝑛+3 = 9, то 2𝑛−1 =
Ответ: 363.
9
3
2
22
𝑛−1 ∙ 222 =
4 . Поэтому √2
∙ 222 = 3 ∙ 112 =363.
№7.
(√𝟏𝟐)𝒏 ∙(√𝟏𝟒)𝒏
𝟐𝒏+𝟐 ∙𝟒𝟐𝒏
при n= - 6
Решение.
Преобразуем данное в условии выражение следующим образом:
𝑛
(√2∙√6) ∙(√2∙√7)𝑛
22 ∙2𝑛 ∙42𝑛
=
2𝑛 ∙(√42)𝑛
4∙2𝑛 ∙42𝑛
1
1
4
4
n=-6, имеем: ∙ (√42)6 =
Ответ: 18522.
= 4∙(
1
√42)𝑛
. Подставляя в полученное выражение
∙ 423 = 212 ∙ 42 = 18522.
Самостоятельная работа № 2.
Рациональные выражения, корень, степень.
Вариант № 1.
1
7
3
9
1. ( + 5 ) • 13,5
2. 10a − 2b + 8, если
3
a+3b+1
3a+b−1
=2
3
3
3. √14 − √115 • √14 + √115 • √243
4.
√0,3•√0,375
√20
5. 96 • 65 : 544
6.
58,5
1253,5
2
7.
3
m5 •m7
при m=32
8
m35
Вариант № 2.
2
5
1. ( + 1 ) • 10.5
7
6
2. 10а − 4𝑏 + 5, если
6
6
7а−6𝑏+5
3𝑎−2𝑏−1
=4
6
3. √7 − √17 • √7 + √17 • √128
4.
√0.15•√13.5
√10
5. 67 • 85 : 486
6.
272.3
33.9
2
7.
13
𝑚3 •𝑚14
2
𝑚21
при m=49
Вариант № 3.
1
1
+ 2 ) • 5.5
11
5
1. (
2. 12.5a + 5b + 21, если
3
4a+3b
3a+4b+1
= 0.5
3
3
3. √0.1 − √0.001 • √0.1 + √0.001 • √3
4.
√1.4•√6.3
√0.18
5. 0.12 • 0.23 : 0.54
1
2
6. (0.0646 • 0.4−3.5 )−3
6
7.
3
√a• √a
,
a18
если a70 = 625
Вариант № 4.
1
5
2
7
1. ( + 3 ) • 12.6
2. a+2.5b +12, если
4
0,2𝑎+0.3𝑏−44
0.4𝑎+0.5𝑏+90
4
= 0.4
4
3. √0.5 − √0.2 • √0.5 + √0.2 • √1.25
4.
√1.2•√3.3
√0.44
5. 0.211 • 0.314 : 0.0612
1
1
6. (0.125−12 • 0.59.25 )3
5
7.
20
√𝑎• √𝑎
,
𝑎25
если 𝑎99 = 256
Вариант № 5.
1.
2.
28
0.3
1.5
•
0.56
4
𝑎3 𝑏−𝑎𝑏
3:
2
𝑎𝑏5 −𝑎5 𝑏
6
1
при 𝑎 = 0.2, 𝑏 = 0.3
3
3. (√3 − √5 ) : √
7
4
28
4
12
4. 0.5 • √125 • √125
5. (7•2−5 ) • (8 • 5−3 )
2
4
9
6. 311 • 411 • 4811
7.
18𝑛−1
3𝑛+1
, если 6𝑛 = 81
Вариант № 6.
1.
2.
0.36
47
•
9.4
0.09
1
𝑎2 𝑏+𝑎𝑏
2:
1
5
𝑎2 𝑏4 −𝑎4 𝑏2
2
7
3.
(√4 5 − √11 3) : √60
4.
5.
12 • √121 • √121
(3•2−6 ) • (6 • 5−4 )
6.
0.47 • 57 • 107
3
3
7.
12𝑛+1
4 𝑛−2
при а = 0,1, 𝑏 = 0.9
6
6
4
, если 3𝑛 = 15
Вариант № 7.
1.
2.
0.28
•
0.77
4.9
44
2
𝑥 +2𝑥−24
𝑥 2 −4𝑥
6
при 𝑥 = 0.003
1
3
3. (√ − √10 ) : √
7
2
56
5
10
4. √81 • √9
5. (5 · 2−5 )•(24·25−3 )
6. 0.7.03 • 490.35 • 101.3
𝑛+2
7.
(√30)
(√6)
𝑛−4
если 5𝑛 = 64
Вариант № 8.
1.
2.
0.35
•
5.4
45
84
2
𝑥 −2𝑥−15
𝑥 2 +3𝑥
1
при 𝑥 = 0.02
2
11
3. (√27 − √4 ) : √
2
5
90
3
9
4. √32 • √8
5. (9 • 4−3 ) • (44 • 5−5 )
6. 0.20.1 • 0.080.3 • 10−1.3
𝑛+1
7.
(√78)
(√13)𝑛−3
, если 6𝑛 = 54
Вариант № 9.
1
3
2
6
1. (1 + ) • (2 − )
2
5
3
7
2.
𝑥 4 −6𝑥 2 −16
при 𝑥 = 0.8
𝑥 2 +2
3. √22 + 12√2 + √99 − 54√2
8
4
4. 16• √0.081 • √0.01
5. 84 • 95 : 126
1
5
2
5
6. 0.15 • 9 • 20
7.
(√22)𝑛 •(√55)𝑛
11
5
при 𝑛 = −8
11𝑛−2• 10𝑛+2
Вариант № 10.
2
4
1
7
1. (1 + ) • (2 − )
5
7
3
8
2.
x8 +x4 −72
x4 −8
при 𝑥 = 0.9
3. √36 − 16√5 − √45 + 20√5
5
20
4. 20 • √0.0001 • √0.0001
5. 45 • 64 : 4803
1
2
4
6. 0.67 • 277 • 257
𝑛
7.
(√15)𝑛 •(√21)
3𝑛−3 •35𝑛+5
при 𝑛 = −12
Ответы к работе № 2.
№задания
Вариант
1
Вариант
2
Вариант
3
Вариант
4
Вариант
5
Вариант
6
Вариант
7
Вариант
8
Вариант
9
Вариант
10
1
82,5
2
14
3
27
4
0,075
5
486
6
0,04
7
8
22,25
23
4
0,45
0,75
27
343
12,6
23,5
0,3
7
0,00128
0,16
0,2
53,1
2012
0,5
3
0,45
0,125
0,25
250
-0,26
-1
2,5
0,014
48
1,5
0,8
0,0144
-4
132
0,00045
10
2880
0,001
2001
-10
3
0,00024
70
8640
0,0005
-249
9
4
0,00198
0,02
3042
3,8
-7,36
11
4,8
81
1200
12100
2,875
9,6561
-9
2
0,012
15
945
Самостоятельная работа №3.
«Тригонометрические выражения».
Рекомендуемое время для выполнения работы 40 минут.
Вариант 1.
1. 11 – 99𝑐𝑜𝑠 2 x, если 𝑠𝑖𝑛2 x = 0,9
2.
𝑠𝑖𝑛𝛼
√5
, если 𝑡𝑔 𝛼 = 2 и 𝛼 Є (π; 2π)
3. √32 • 𝑠𝑖𝑛
4.
33𝜋
4
• 𝑐𝑜𝑠
34𝜋
3
1−2𝑐𝑜𝑠2 111˚
10𝑐𝑜𝑠2 114˚•𝑡𝑔66˚
5. √6 •
𝑠𝑖𝑛20˚𝑐𝑜𝑠40˚+𝑠𝑖𝑛110˚𝑠𝑖𝑛40˚
𝑠𝑖𝑛10˚𝑠𝑖𝑛35˚−𝑠𝑖𝑛100˚𝑐𝑜𝑠35˚
Вариант 2.
1. 13 - 12 𝑠𝑖𝑛2 x, если 𝑐𝑜𝑠 2 𝑥 = 0,11
2.
√17
,
𝑐𝑜𝑠𝛼
если 𝑐𝑡𝑔 𝛼 = −4 и 𝛼 Є (
3. √6 • 𝑠𝑖𝑛
4.
63𝜋
4
• 𝑡𝑔
64𝜋
3
1−2𝑠𝑖𝑛2 54˚
8𝑡𝑔9˚•𝑠𝑖𝑛2 99˚
5. √2 •
𝑠𝑖𝑛40˚𝑐𝑜𝑠5˚−𝑠𝑖𝑛230˚𝑠𝑖𝑛5˚
𝑠𝑖𝑛25˚𝑠𝑖𝑛35˚−𝑠𝑖𝑛115˚𝑐𝑜𝑠35˚
3𝜋 5𝜋
2
;
2
)
Вариант 3.
1. 2-3𝑐𝑜𝑠 2 𝑥, если sin 𝑥 = −0,4
2. √13•sin α, если tg α = -1,5 и α Є (2π;3π)
3. ctg
4.
5.
43𝜋
4
• 𝑐𝑜𝑠
43𝜋
3
• 𝑠𝑖𝑛
43𝜋
6
𝑠𝑖𝑛2 1135˚−𝑠𝑖𝑛2 35·
𝑠𝑖𝑛350˚•𝑐𝑜𝑠370˚
𝑠𝑖𝑛70˚𝑐𝑜𝑠40˚−𝑠𝑖𝑛160˚𝑠𝑖𝑛40˚
𝑠𝑖𝑛20˚𝑠𝑖𝑛80˚+𝑠𝑖𝑛110˚𝑐𝑜𝑠80˚
Вариант 4.
1. 4𝑠𝑖𝑛2 𝑥 − 3, если cos 𝑥 = 0,2
𝜋 3𝜋
2. √53 ∙ cos 𝛼 , если 𝑐𝑡𝑔 𝛼 = 3,5 и 𝛼 𝜖 ( ;
2
3. 𝑡𝑔
4.
5.
57𝜋
4
∙ sin
59𝜋
6
∙ 𝑐𝑜𝑠
61𝜋
3
𝑐𝑜𝑠 2 200°−𝑐𝑜𝑠 2 1010°
𝑐𝑜𝑠565°∙𝑐𝑜𝑠605°
√2 𝑠𝑖𝑛35°𝑠𝑖𝑛80°+𝑠𝑖𝑛125°𝑐𝑜𝑠80°
∙
4 𝑠𝑖𝑛10°𝑐𝑜𝑠20°−𝑐𝑜𝑠170°𝑠𝑖𝑛20°
2
)
Вариант 5.
1. 54𝑐𝑡𝑔2 𝑥, если sin 𝑥 = 0,3
√6
3
2.
√2 ∙ 𝑡𝑔 𝛼, если cos 𝛼 =
3.
𝑡𝑔240° ∙ sin 480° ∙ 𝑐𝑜𝑠960°
4.
и 𝛼 𝜖 (𝜋; 2𝜋)
sin 560°
𝑠𝑖𝑛400°𝑐𝑜𝑠800°𝑠𝑖𝑛770°
𝑠𝑖𝑛75°𝑐𝑜𝑠°15−𝑠𝑖𝑛165°𝑠𝑖𝑛15°
5. √3 ∙ 𝑠𝑖𝑛35°𝑠𝑖𝑛205°+𝑠𝑖𝑛305°𝑐𝑜𝑠205°
Вариант 6.
1. 8ctg 2 x + 7, если 𝑐𝑜𝑠𝑥 = −0,6
1
𝜋 3𝜋
2. √2 ∙ ctg α, если sin 𝛼 = 3 и 𝛼 𝜖 ( 2 ; 2 )
3. 𝑡𝑔300° ∙ 𝑠𝑖𝑛600° ∙ 𝑐𝑜𝑠900°
4.
cos670°
cos755° cos755° cos650°
sin10° cos55° + sin280° sin55°
5. √6 ∙ sin10° cos110° + sin260° cos200°
Вариант 7.
1.
tg 2 α, если 10𝑠𝑖𝑛2 𝛼 + 71𝑐𝑜𝑠 2 𝛼 = 35
2.
√6
,
cos 𝛼
3.
𝑐𝑡𝑔300° ∙ 𝑐𝑜𝑠600° ∙ 𝑠𝑖𝑛1200°
4.
(𝑠𝑖𝑛4
5.
если 𝑐𝑡𝑔 𝛼 = √2 и 𝛼 𝜖 (𝜋; 2𝜋)
35𝜋
24
− 𝑠𝑖𝑛4
25𝜋
24
) ∙ 𝑠𝑖𝑛
25𝜋
12
∙ 𝑠𝑖𝑛
25𝜋
6
)
𝑠𝑖𝑛5°𝑐𝑜𝑠25° + 𝑠𝑖𝑛95°𝑠𝑖𝑛25°
𝑠𝑖𝑛15° 𝑐𝑜𝑠105° − 𝑠𝑖𝑛105° 𝑠𝑖𝑛75°
Вариант 8.
1.
𝑐𝑡𝑔2 𝛼, если 88𝑠𝑖𝑛2 𝛼 − 90𝑐𝑜𝑠 2 𝛼 = 10
2.
√30 ∙ sin 𝛼 , если 𝑡𝑔 𝛼 = √5 и 𝛼 𝜖 (2 ; 2 )
3.
𝑡𝑔600° ∙ 𝑠𝑖𝑛1200° ∙ 𝑐𝑜𝑠2400°
𝜋 3𝜋
4. (𝑐𝑜𝑠 2
23𝜋
16
− 𝑐𝑜𝑠 2
33𝜋
16
) ∙ 𝑠𝑖𝑛
33𝜋
8
∙ 𝑠𝑖𝑛
𝑠𝑖𝑛25° 𝑐𝑜𝑠85° + 𝑠𝑖𝑛245° 𝑠𝑖𝑛85°
5. √6 ∙ 𝑠𝑖𝑛20° 𝑠𝑖𝑛65° − 𝑠𝑖𝑛290° 𝑐𝑜𝑠65°
33𝜋
4
Вариант 9.
1.
cos 2𝛼, если 𝑡𝑔𝛼 = −0,75
2.
√6 ∙ sin 𝛼, если cos 𝛼 = 0,2 и 𝛼 𝜖 ( 2 ; 2𝜋)
3.
𝑡𝑔690° ∙ 𝑐𝑜𝑠1200° ∙ 𝑠𝑖𝑛1500°
4.
𝑐𝑜𝑠
𝜋
2𝜋
7
∙ 𝑐𝑜𝑠
5. 𝑡𝑔210° ∙
3𝜋
7
∙ 𝑐𝑜𝑠
6𝜋
7
𝑠𝑖𝑛10° 𝑐𝑜𝑠410° − 𝑠𝑖𝑛1700° 𝑠𝑖𝑛50°
𝑠𝑖𝑛20° 𝑠𝑖𝑛400 + 𝑠𝑖𝑛70° 𝑐𝑜𝑠500°
Вариант 10
1. sin 2α, если tg α = - 3
𝜋
2. √21 • cos 𝛼, если sin 𝛼 = 0,4 и 𝛼 Є ( ; 2𝜋)
2
3. ctg 1020 ˚• cos 1230˚•cos 2340˚
4. 𝑠𝑖𝑛
𝜋
14
• 𝑠𝑖𝑛
5. ctg 1110˚•
3𝜋
14
•
5𝜋
14
sin 1100˚𝑠𝑖𝑛50˚+ sin 1150˚ sin 400˚
sin 110˚ sin 10˚− sin 200˚ sin 2240˚
Решение примеров к работе № 3.
20 𝒄𝒐𝒔
𝝅
𝟕
𝟐𝝅
• 𝒄𝒐𝒔
𝟕
• 𝒄𝒐𝒔
𝟒𝝅
𝟕
Решение:
𝜋
Умножив данное в условия выражение на sin и применив трижды формулу синуса
7
двойного угла, получим:
𝜋
𝜋
2𝜋
7
7
7
(20𝑠𝑖𝑛 • 𝑐𝑜𝑠 ) • 𝑐𝑜𝑠
5 sin
4𝜋
7
• 𝑐𝑜𝑠
4𝜋
7
5
8𝜋
2
7
= 𝑠𝑖𝑛
• 𝑐𝑜𝑠
4𝜋
7
= (10𝑠𝑖𝑛
2𝜋
7
• 𝑐𝑜𝑠
2𝜋
5
𝜋
5
𝜋
2
7
2
7
7
) • 𝑐𝑜𝑠
4𝜋
7
=
= sin (𝜋 + ) = − 𝑠𝑖𝑛 .
Следовательно, данное в условии выражение до умножения на sin
𝜋
7
было равно - 5/2.
Ответ: - 2,5.
√𝟒𝟖 •
𝐜𝐨𝐬𝟕𝟔𝟓˚ • (𝐜𝐨𝐬𝟑𝟒𝟓˚ − 𝐬𝐢𝐧𝟓𝟓𝟓˚)
𝐜𝐨𝐬𝟕𝟕𝟓˚ • 𝐬𝐢𝐧𝟒𝟒𝟓˚ + 𝐬𝐢𝐧𝟑𝟓𝟓˚ • 𝐜𝐨𝐬𝟕𝟓𝟓˚
Решение:
Используя формулы приведения, упростим числитель данной в условии дроби:
cos765˚ = cos (360˚•2+45˚) = cos45˚; cos345˚ = cos (360˚ - 15˚) = cos15˚ ; sin 555˚ =
sin(180˚• 3+15˚) = - sin 15˚. Итак, числитель данной в условии дроби равен
cos45˚•(cos15˚ + sin15˚). Заметим, что поскольку cos45˚= sin45˚, то раскрыв скобки и
применив формулу косинуса суммы, получим: cos45˚•(cos15˚+sin15˚) =
cos45˚•cos15˚+sin45˚•sin15˚ = cos(45˚-15˚) = cos30˚ =
√3
.
2
Теперь упростим и преобразуем знаменатель данной в условии дроби:
cos775˚ = cos (360˚•2+55˚) = cos 55˚; sin 445˚= sin (360˚ + 85˚)= sin 85˚=cos 5˚; sin 355˚=
sin (360˚ - 5˚)= - sin 5˚; cos 755˚ = cos(360˚ ∙ 2 + 35˚) = cos 35˚ = sin 55˚. Итак,
знаменатель данной в улови дроби равен cos 55˚ · cos 5˚ − sin 5˚ · sin 55˚ =
1
cos(55˚ + 5˚) = cos(55˚ + 5˚) = cos 60˚ = . Поэтому значение данного в условии
2
выражения равно √48 ∙
Ответ: 12.
√3 1
:
2 2
= √48 ∙ √3 = √144 = 12.
𝐬𝐢𝐧 𝟐𝜶, если
𝟓 𝐬𝐢𝐧 𝜶−𝟔 𝐜𝐨𝐬 𝜶
𝟔 𝐬𝐢𝐧 𝜶−𝟏𝟎 𝐜𝐨𝐬 𝜶
= 𝒕𝒈𝜶.
Решение:
sin α
5 sin α−6 cos α
tg α =cos α = 6 sin α−10 cos α
отсюда по правилу пропорции имеем :
sin α·(6 sin α – 10 cos α = cos α · (5 sin α – 6 cos α). Раскрывая скобки и преобразовывая
полученное равенство , находим :
6 sin2 α – 10 sin α cos α = 5 sin α cos α – 6 cos2α, 15 sin α cos α =
= 6 sin2 + 6 cos2α = 6. Отсюда находим , что значение искомого выражения равно sin2α
6
4
= 2sin α cos α =2· = = 0,8
15
Ответ: 0,8
5
Ответы к работе №3
№ задания
1
2
3
4
5
Вариант 1
1,1
-0,4
-2
0,2
-3
Вариант 2
2,32
4,25
-3
-0,25
-2
Вариант 3
-0,52
3
0,25
-2
1
Вариант 4
0,84
-7
-0,25
2
0,5
Вариант 5
546
-1
-0,75
-4
3
Вариант 6
11,5
-4
-1,5
4
-2
Вариант 7
1,44
-3
0,25
0,125
-0,5
Вариант 8
0,78
-5
-0,75
-0,25
-3
Вариант 9
0,28
-2,4
0,25
-0,125
-1
Вариант 10
-0,6
-4,2
-0,5
0,125
3
Решение примеров работы №4.
№1
log2,25 log18 (54√𝟐)
Решение.
3
Заметим, что 54√𝟐 = 18 · 3√𝟐 = 18√𝟏𝟖. Поэтому log18 (54√𝟐) = log18 (182 ) = 1,5.
1
Далее имеем : 2,25 = 1,52 , log2,25 log18 (54√𝟐) = log2,25 1,5 = log1,52 1,5 = log1,5 1,5 = 0,5
2
Ответ: 0,5
№2
log910 · log8729 ·lg 128
Решение:
так как 8 = 23, 729 = 93 , то log8 729 = log23 93 = log2 9. Далее 128 = 27 , lg 128 = lg 27 = 7lg2.
Поэтому данное в условии выражение преобразуется следующим образом :
log9 10 · log2 9 · 7 lg 2 =
7𝑙𝑜𝑔9 10
𝑙𝑜𝑔9 2
· lg 2 = 7 log2 10 · lg 2 =
7𝑙𝑜𝑔2 10
𝑙𝑜𝑔2 10
=7
Ответ : 7.
№3
𝟔
logα√𝛂√𝐛 , если а9 – b5 = 0
Решение:
1 1
1
9
1
√α 6√b = (𝑎 · 𝑏 6 )2 = а 2 · 𝑏 12 . По условию имеем : a9 = b5 , b = 𝑎 5 .
Отсюда получаем : а
1
2
·𝑏
1
12
1
2
1
9 12
5
= а ·(𝑎 )
13
13
6
Итак, log 𝑎 √𝑎 √𝑏 = log 𝑎 (𝑎20 ) = = 0,65.
20
Ответ: 0,65
1
3
1
3
13
= 𝑎2 ∙ 𝑎20 = 𝑎2+20 = 𝑎20 .
№4.
𝐥𝐨𝐠 𝟐𝟐 𝟗𝟔 ∙
(𝐥𝐨𝐠 𝟐 𝟏𝟐 − 𝟑)𝟐
𝐥𝐨𝐠 𝟏𝟐 𝟐 −
𝐥𝐨𝐠 𝟐 𝟏𝟐
Решение:
3
Так как log 2 12 − 3 = log 2 12 − log 2 8 = log 2 , то данное в условии выражение
2
преобразуется следующим образом:
log 22 96 ∙
1
log 22 1,5 log 22 96 − log 22 1,5 (log 2 96 − log 2 1,5) ∙ (log 2 96 + log 2 1,5)
−
=
=
=
log 2 12 log 2 12
log 2 12
log 2 12
log 2 64 ∙ log 2 144 log 2 26 ∙ log 2 122 6 ∙ 2 ∙ log 2 12
=
=
=
= 12.
log 2 12
log 2 12
log 2 12
Ответ: 12.
Самостоятельная работа №4. Логарифмические выражения.
Рекомендуемое время для выполнения работы 35 минут.
Шкала оценивания результатов
число верных ответов
оценка
0-1
2
Вариант 1
1. log 2 12,8 − log 2 0,8
2. 36log6 0,3
3. log100 4√0,1
4. log 0,2 log 2 32
5. log 𝑎 (𝑎12 𝑏13 ), если log 𝑏 𝑎 =
1
3
Вариант 2
1. log 3 32,4 − log 3 1,2
2. 81log9 0,2
6
3. log 49 √343
4. log 0,5 log 5 625
𝑎4
1
5. log 𝑎 ( 3 ), если log 𝑏 𝑎 =
6
𝑏
2
3
3
4
4-5
5
Вариант 3
1. log 5 0,6 − log 5 3
2. 27log3 0,3
5
3. log 0,5 √64
4. log 81 log 9√2 8
5. log 𝑏 (𝑎6 𝑏 99 ), если
1
2
log а в = 0,6
Вариант 4
1. log 2,5 25 − log 2,5 4
2. 8log2 0,4
4
3. log 0,2 √125
4. log 4 log 8√3 81
5. log 𝑎 (𝑎4 𝑏 32 ), если
1
2
log 𝑏 𝑎 = 0,1
Вариант 5
1. lg 0,0025 + lg 0,004
2. 49log√7 4
4
3. log 4 (8√8)
3
4. log 9 log 54 (3√2)
5
4
6
5. log 𝑏 ( √𝑎 ∙ √𝑏), если log 𝑏 √𝑎 = 7
Вариант 6
1. log 5 0,032 + log 5 1,25
2. 4log√2 6
8
3. log 64 (8√8)
5
4. log 0,4 log 343 (7√7)
6
5
4
5. log 𝑏 ( √𝑎 ∙ √𝑏), если log 𝑏 √а = 3
Вариант 7
1. log 2 312,5 + log 2 0,000 4
2. 144log√12 3
4
3. log16 (4√0,5)
5
4. log 0,04 log 64 (2√2)
6
5. log 𝑎 √𝑎 √𝑏 , если 𝑏 2 − 𝑎3 = 0
Вариант 8
1. log 4 2,56 + log 4 6,25
2. 169log√13 2
3. log 0,04 (5 4√0,2)
5
4. log 2,5 log 27 (3√3)
8
5. log 𝑎 √𝑎3 √𝑏, если 𝑏 5 − 𝑎4 = 0
Вариант 9
1. log 6 54 + log 6 144
2. (2√2)
log√2 11
3. log 0,05 (40√5)
4. log 3 0,04 ∙ log 5 49 ∙ log 7 27
5. lg 2 9000 ∙ log 3 10 −
(3−lg9)2
lg3
Вариант 10
1. log14 56 + log14 686
2. (9√3)
log√3 6
3. log 0,08 (2,5√2)
4. log 3 32 ∙ log 2 25 ∙ log 0,2 3
5.
log22 3
log2
−
12
log2 48∙log12 2
log48 2
Ответы к работе № 4 «Преобразование логарифмических выражений».
№ задания
1
2
3
4
5
Вариант 1
4
0,09
-0,125
-1
51
Вариант 2
3
0,04
0,25
-2
-14
Вариант 3
-1
0,008
-1,2
0,75
104
Вариант 4
2
0,064
-0,75
2,5
164
Вариант 5
-5
256
1,875
-0,5
10,7
Вариант 6
-2
1296
0,5625
1
2,2
Вариант 7
-3
81
0,4375
0,5
0,625
Вариант 8
2
16
-0,375
-1
1,55
Вариант 9
5
1331
-1,5
-12
24
Вариант 10
4
7776
-0,5
-10
-8
Примеры решения уравнений .
x2 - 4x + 6 =
𝟓
𝟒𝒙−𝒙𝟐
(В ответе укажите сумму всех различных действительных корней данного уравнения).
Решение: Введём новое неизвестное t = x2 – 4x . Относительно неизвестного t, данное
в условии уравнении, имеет вид: t +6 = –
5
𝑡
,
𝑡 2 + 6𝑡+5
𝑡
= 0.
Корнями этого уравнения являются t1 = - 5 и t2 = - 1. Возвращаясь к неизвестному x ,
получаем , что исходное уравнение равносильно совокупности двух уравнений :
x2 – 4x + 5 = 0
и
x2 – 4x + 1 = 0 . Первое их этих уравнений корней не имеет, а
второе имеет два различных корня, сумма которых по теореме Виета равна 4.
Ответ: 4.
√𝒙𝟐 − 𝟗𝒙 + 𝟏𝟖 + √𝒙𝟑 − 𝟔𝒙 − 𝟗 = 0. (Если уравнение имеет более одного корня, то в
ответе укажите наибольший из его корней.)
Решение: Так как квадратный корень неотрицателен по определению , то сумма двух
квадратных корней может быть равна нулю . Поэтому данное в условие уравнение
равносильно системе двух уравнений :
2
{𝑥 3 − 9𝑥 + 18 = 0 ,
𝑥 − 6𝑥 − 9 = 0
Корнями первого из этих уравнений являются x = 3 и x = 6. Подставляя поочерёдно
найденные корни в уравнение (2),находим :
x = 3 является его корнем, а x = 6 – нет.
Ответ: 3.
3x2 + √𝒙𝟒 − 𝟒𝒙𝟐 = 12 (Если уравнение имеет более одного корня, в ответе укажите
наибольший из его корней.)
Решение:
Приведём данное в условии уравнение к виду: √𝑥 2 − (𝑥 2 − 4) = 12 – 3x2 ,
|𝑥| · √𝑥 2 − 4 = 3 · (4 – x2). Так как левая часть уравнения неотрицательна , то правая
его часть также должна быть неотрицательна, то есть для корней уравнения
выполнено неравенство 4 – x2 ≥ 0 , x2 ≤ 4. С другой стороны , в область определения
уравнения входят лишь те x, для которых x2 – 4 ≥ 0 , x2 ≥ 4. Из неравенств x2 ≤ 4 и
x2 ≥ 4 следует , что корнями уравнения являются лишь корни уравнения x2 = 4, т.е.
x = ± 2.
Ответ: 2.
𝟑
√𝒙 + 𝟐 =√𝟓𝒙 + 𝟏𝟎 (Если уравнение имеет более одного корня, в ответе укажите
произведение всех корней уравнения)
Решение:
3
3
3
√5𝑥 + 10 = √5 · √𝑥 + 2. Введём новое известное t, такое, что x + 2 = t6 , t ≥ 0.
Относительно неизвестного t данное в условии уравнение имеет вид:
3
3
√𝑡 6 = √5 · √𝑡 6
3
3
t3 = √5 · √𝑡 6
3
t3 = √5 · t2
3
t2 · ( t · √5) = 0
Возвращаясь к неизвестному x, получаем , что исходное уравнение равносильно
совокупности:
𝑥+2=0
[
3
𝑥 + 2 = (√5)6
↔
𝑥 = −2
[
𝑥 = 23
Поэтому произведение всех корней уравнение равно – 46
Ответ : - 46 .
𝟐
𝒙−𝟕
𝒙
𝟕
+ 𝟐𝟑− 𝒙 = 160
Решение:
Преобразуем данное уравнение следующим образом :
1−
2
7
𝑥
+2
𝟕
3−
𝟕
𝒙
= 160
𝟕
2 · 2 − 𝒙 + 23− 𝒙 = 160
(2 + 8) · 2
−
𝟕
𝒙
= 160
𝟕
2 − 𝒙 = 16. Отсюда имеем: −
7
𝑥
= 4, отсюда x = −
7
4
Ответ: - 1,75.
9x + 5 = 0,03 · 102X + 11
Решение.
Заметив , что 9x + 5 =32(x+5) и 102x + 11 = 10 · 102x + 11 , преобразуем данное в условии
уравнение к виду :
32(x+5)
102(x+5)
= 0,3, 0,32(x + 5) = 0,3. Отсюда следует , что 2(x + 5) = 1 , x = - 4,5
Ответ : -4,5.
27 · 5x + 20 · 9x – 45x – 540 = 0 (Если уравнение имеет более одного корня, в ответе
укажите меньший из его корней.)
Решение :Группируя первое слагаемое м третьим , а второе с четвёртым и вынося за
скобки общий множитель , получим : 5x · (27 – 9x) + 20 · (9x -27) = 0
(5x – 20 ) · (27 – 9x) = 0. Таким образом, данное в условии уравнение равносильно
совокупности:
[
𝑥 = 𝑙𝑜𝑔5 20
5𝑥 − 20 = 0
⟺ [
𝑥
𝑥 = 𝑙𝑜𝑔9 27
27 − 9 = 0
Заметим, что log5 20 = 1+ log 5 4
3
log927 = 𝑙𝑜𝑔32 33 = = 1,5. Так как 1,5 < 1 + log5 4, то меньшим корнем уравнения
2
является x =1,5
для полноты решения докажем, что 1,5 < 1 + log5 4. Имеем следующую цепочку
равносильных неравенств : 1,5 < 1 + log5 4 ⟺ 0,5 < log5 4 ⟺ 50,5 < 4, √5 < 4 – верное
неравенство, что и требовалось доказать.
Ответ: 1,5.
𝒍𝒐𝒈𝟐𝟐 (32x) – 78 𝒍𝒐𝒈𝟖 𝒙 = 22 (Если уравнение имеет более одного корня, в ответе
укажите произведение всех корней уравнения.)
Решение: Так как log2(32x) = log2 (25 · x) = 5 + log2 x и log8 x = 𝑙𝑜𝑔 23 𝑥 =
1
3
log2 x , то
данное уравнение преобразуется к виду : (5 + log2 x)2 – 26 log2 x = 22. Введём новое
неизвестное t =log2x. Относительно неизвестного t уравнение имеет вид:
(t + 5)2 – 26t = 22
t2 – 16t + 3 = 0. Данное уравнение имеет два различных корня t1 t2
Возвращаясь к неизвестному x, получаем, что исходное уравнение равносильно
совокупности уравнений log2 x = t1 и log2 x = t2 Следовательно, корнями исходного
уравнения являются числа x1 = 2𝑡1 и x2 =2𝑡2 . Перемножая эти равенства, получаем :
x1 · x2 = 2𝑡1 + 𝑡2 Осталось заметить, что по теореме Виета t1 + t2 = 16, поэтому
x1 · x2 = 216 = 210 · 26 = 1024 · 64 = 65536.
Ответ : 65536.
log3 ( x2 + 10x – 144 ) - log9 ( x2 + 36x + 324 ) = 14 (Если уравнение имеет более одного
корня, в ответе укажите сумму всех корней уравнения.)
Решение.
заметим, что x2 + 10x - 144 = (x + 18) · (x - 8), a x2 + 36x + 324 = (x + 18)2 . Поэтому
log9 (x2 + 36x +324) = 𝑙𝑜𝑔32 (x + 18)2 = log3 |𝑥 + 18| и данное в условии уравнение
преобразуется к виду: log3 (( x + 18) · ( x – 8 )) – log3 |𝑥 + 18| = 14
log3
(𝑥+18) ·(𝑥−8)
|𝑥+18|
(𝑥+18) ·(𝑥−8)
|𝑥+18|
= 14
= 314 Если x > - 18, то
𝑋+18
|𝑥+18|
= 1 и уравнение упрощается к виду x – 8 = 314
𝑋+18
Если x < -18, то |𝑥+18| = - 1, уравнение упрощается к виду x – 8 = - 314
откуда x =8 – 314 . Так как для чисел x1 = 8 + 314 и x2 = 8 – 314 выполнены условия x1 > 18
и x2 < -18, то они действительно являются корнями исходного уравнения, а их сумма
равна 8 + 314 + 8 – 314 = 16.
cos 7x +cos 8x + cos 9x = 0 (В ответе запишите величину наименьшего положительного
корня уравнения , выраженную в градусах. )
Решение.
Так как cos 7x + cos 9x = 2 cos
7𝑥+9𝑥
2
· 𝑐𝑜𝑠
9𝑥−7𝑥
2
= 2 cos 8x · cos x , то данное в условии
уравнение преобразуется к виду:
2 cos 8x · cos x + cos 8x = 0
cos 8x · (2 cos x + 1 ) = 0 и значит, оно равносильно совокупности уравнений cos 8x = 0
𝜋
и 2 cos x = - 1. Корнями уравнения cos 8x = 0 являются те x, для которых 8x + 𝜋𝑛,
или x =
𝜋
16
+
𝜋𝑛
является x =
2
, где n∈ 𝑍 ⇒ наименьшим положительным корнем этого уравнения
8
𝜋
, что в градусах составляет
16
180𝑜
16
корнями уравнения cos x = - 0,5 являются x ±
= 11,25𝑜
2𝜋
3
+ 2𝜋𝑛, где 𝑛 ∈ Z ⇒ наименьшим
положительным корнем этого уравнения является x =
1200.
Ответ: 11,25.
2𝜋
3
, что в градусах составляет
Работа № 5 .
Рациональные и иррациональные уравнения .
Вариант № 1.
1)
12
21
x = -2
6
21
2) x2 + 6x + 11 +
18
𝑥 2 + 6𝑥
=0 (В ответе укажите сумму всех различных корней данного
уравнения )
3) 3√0,1 х − 0,2 = 0,3
4)√4𝑥 + 3 = 2x (Если уравнение имеет несколько корней, то в ответе укажите
произведение их корней )
5) √72 − 2𝑥 − 𝑥 3 + √𝑥 2 − 6𝑥 + 8 = 0 (Если уравнение имеет несколько корней, то
укажите наименьший из них) .
Вариант № 2.
1)
2
3
𝑥=–4
1
3
2) x2 – 8x + 18 +
32
𝑥 2 − 8𝑥
= 0 (В ответе укажите сумму всех различных корней данного
уравнения .)
4
3) √5𝑥 − 6 = 7
4) √6𝑥 + 4 = – 2x (Если уравнение имеет несколько корней, в ответе укажите их
произведение.)
5) √𝑥 3 − 7𝑥 − 90 + √𝑥 2 − 12𝑥 + 35 = 0 (Если уравнение имеет несколько корней, в
ответе укажите наибольший из них.)
Вариант № 3.
1)
2)
12
13
x=–4
22
x2 − 8x+9
5
13
+ 8x – x2 = 0 (В ответе укажите сумму всех различных корней данного
уравнения .)
3
3) √6 − 3𝑥 = 6
4) √41 − 4𝑥 =3 – 2x (Если уравнение имеет несколько корней, в ответе укажите их
произведение.)
5) 5x3 + √𝑥 5 − 27𝑥 2 = 135 (Если уравнение имеет несколько корней, в ответе укажите
наибольший из них.)
Вариант № 4.
1)
2)
13
57
x=9
33
57
16
6+4𝑥−𝑥 2
+ x2 – 4x = 0 (В ответе укажите сумму всех различных корней данного
уравнения.)
7
3 ) √2 − 7𝑥 = 2
4) √8𝑥 − 7 = 6 – 5x (Если уравнение имеет несколько корней, в ответе укажите их
произведение.)
5) 9x4 + √𝑥 6 − 16𝑥 2 = 144 (Если уравнение имеет несколько корней, то укажите
наименьший из них.)
Вариант № 5.
1)
𝑥+1
𝑥+1
=
𝑥 2 − 3𝑥
9𝑥 2 − 15𝑥
(В ответе укажите сумму всех различных корней данного
уравнения.)
2)
8
𝑥
-
4
+2=
𝑥−1
1
𝑥 − 𝑥2
( В ответе укажите произведение всех различных корней
данного уравнения.)
3) √
3
5𝑥− 7
=
1
9
4) √21 − 2𝑥 = 1 – 2x (Если уравнение имеет несколько корней, в ответе укажите их
сумму .)
5) 0,25x2 · √𝑥 − 4 =√625𝑥 − 2500 ( В ответе укажите произведение всех различных
корней данного уравнения.)
Вариант № 6.
1)
𝑥+0,4
=
𝑥 2 + 0,1𝑥
𝑥+ 0,4
0,2𝑥 2 + 0,3𝑥
(В ответе укажите сумму всех различных корней данного
уравнения)
2)
3
5
−
−
𝑥−1
𝑥+1
13
8 = 1− 𝑥2 ( В ответе укажите произведение всех различных корней
данного уравнения.)
3) √
0,5
2𝑥−4
=
1
8
4) √33 − 4𝑥 =3 – x (Если уравнение имеет несколько корней, в ответе укажите их
сумму. )
5) 0,16𝑥 2 · √𝑥 + 4 = √16𝑥 + 64 (В ответе укажите произведение всех различных
корней данного уравнения.)
Вариант №7.
1)
𝑥 +14
𝑥2 − 4𝑥
𝑥 +14
=
6𝑥2 − 8𝑥
(В ответе укажите сумму всех различных корней данного
уравнения .)
2)
2
𝑥+3
−
3
𝑥+4
+
4
𝑥 2 + 7𝑥+12
= 1 (В ответе укажите произведение всех различных
корней данного уравнения.)
3) √
0,01
𝑥+0,1
=
1
11
4) √2013𝑥 − 2012 = x (Если уравнение имеет несколько корней, в ответе укажите их
сумму.)
5) √225 − 𝑥 2 = 0,5x · √𝑥 + 15 ( В ответе укажите произведение всех различных
корней данного уравнения.)
Вариант №8 .
1)
𝑥−9
7𝑥 2 − 5𝑥
=
𝑥−9
3𝑥 2 + 𝑥
(В ответе укажите сумму всех различных корней данного
уравнения .)
2)
4
𝑥−2
+
6
𝑥−4
−
8
𝑥 2 −6𝑥+8
= 10 (В ответе укажите произведение всех различных
корней данного уравнения.)
3)√
0,1
0,2𝑥−3
= 0,4
4) √765𝑥 − 432 =10x (Если уравнение имеет несколько корней, в ответе укажите их
сумму.)
5) √121 − 16𝑥 2 = 6x · √𝑥4 + 11(В ответе укажите произведение всех различных
корней данного уравнения.)
Вариант №9*.
1)
4
3
5
8
6
9
· (𝑥 − ) = 7
2) x4 -
40
𝑥 4 −3𝑥 2
= 3x2 + 6 (В ответе укажите произведение всех различных
действительных корней данного уравнения.)
3) √𝑥 2 + 8𝑥 + 27 = √𝑥 2 + 8𝑥 + 3 ( В ответе укажите сумму всех различных корней
данного уравнения )
4) x2 + 3x – 10 = 5 · (x – 2) · √𝑥 + 1 (В ответе укажите наибольший из корней данного
уравнения.)
3
4
5) √𝑥 + 6 = √8𝑥 + 48 (В ответе укажите сумму всех различных корней данного
уравнения.)
Вариант №10*.
1)
10
11
· (x + 9,8) = 7
2) x4 + 13 = 6x2 –
6
55
36
𝑥 4 − 6𝑥 2
(В ответе укажите произведение всех различных
действительных корней данного уравнения.)
3) √5𝑥 2 + 𝑥 + 12 = √5𝑥 2 + 𝑥 + 2 (В ответе укажите сумму всех различных корней
данного уравнения.)
4) 2x2 + 9x + 4 = (6x + 3) · √𝑥 + 2 (В ответе укажите наименьший из корней данного
уравнения.)
4
5
5) √𝑥 + 5 = √6𝑥 + 30 (В ответе укажите сумму всех различных корней данного
уравнения.)
Ответы к работе № 5«Рациональные и иррациональные уравнения».
№ задания
1
2
3
4
5
Вариант 1
-4
-9
2,27
1,5
4
Вариант 2
-6,5
12
481,4
-0,5
5
Вариант 3
-4,75
16
-70
-2
3
Вариант 4
42
8
-18
1
-2
Вариант 5
0,5
-3,5
50
-2
40
Вариант 6
-0,15
-3,625
18
-4
-20
Вариант 7
-13,2
9
1,11
2013
-90
Вариант 8
8
11,6
18,125
7,65
-1,375
Вариант 9
6,75
-5
-8
15
500
Вариант 10
-1,98
-12
-0,2
-1
1286
Работа №6.
Показательные уравнения.
Вариант № 1.
1) 45x + 6 = 64
2) 81
2𝑥+3
4
=
1
243
3) 0,525x – 4 = 4√2
4) 6x + 6x + 2 = 1332
5) 4x + 1 – 3 · 2x – 1 = 0 (Если уравнение имеет несколько корней, в ответе укажите
меньший из них.)
Вариант №2.
1) 22x – 3 = 32
2) 216
6𝑥+1
21
=
1
36
3) 0,25x +2 = 5√5
4) 4x+3 – 4x = 4032
5) 9x – 8 · 3x + 1 + 63 = 0 (Если уравнение имеет несколько корней, в ответе укажите
меньший из них.)
Вариант №3.
1) 61,2x+3,6 =
2) 0,04
3𝑥−6
7
3) 0,125
1
216
=125
12𝑥−5
42
= 4√2
4) 5x + 5x+3 = 5,04
5) 36x – 37 · 6x – 1 + 1 = 0 (Если уравнение имеет несколько корней, в ответе укажите
сумму всех его корней.)
Вариант №4.
1) 714x – 18 = 343
2) 64
8𝑥−7
24
3) 0,5
4𝑥+3
6
= 0,125
3
= 16 √4
4) 20x+4 + 20x+5 =1,05
5) 9x+2 – 756 · 3x + 243 = 0 (Если уравнение имеет несколько корней, в ответе
укажите произведение всех его корней.)
Вариант №5.
1) 0,25 4x - 3 = 16
2) 5 4 - 5x · 65x - 4 = 1,44
5
3) 0,4 x- 0,3 =6,25 · √2,5
4) 9 x+ 4 = 0,12 · 52x+9
5) 100x – 11 · 10x + 0,5 + 100 = 0 (Если уравнение имеет несколько корней, в ответе
укажите произведение всех его корней.)
Вариант №6.
1) 0,042 - x = 0,008
2) 64x - 3 · 43 – 4x = 2,25
3) 1,25 x - 3 = 0,64 · 4√0,8
4) 1210,5x +1,1 = 0,11 · 10x + 3,2
5) 9x – 10 · 3x + 0,5 + 27 = 0 (Если уравнение имеет несколько корней, в ответе
укажите сумму всех его корней.)
Вариант № 7.
1) 0,08x+2 = 12,5
2) 123x – 2 · 722 – 3x = 7776
4
3) 0,24 – x = 3125 · √125
4) 32x+1 = 0,032 · 55x +6
5) 49x – 9 · 7x – 0,5 + 2 = 0 (Если уравнение имеет несколько корней, в ответе
укажите больший из них.)
Вариант №8.
1) 0,8x+2 = 1,25– 8
2) 64 – 3x · 423x – 4 = 16807
4
3) 0,12x – 3 = 100 · √1000
4) 81x + 1 = 1,125 · 24x + 5
5) 121x – (√11 + 1) · 11x + 0,5 + 11√11 = 0 (Если уравнение имеет несколько
корней, в ответе укажите больший из них.)
Вариант №9*.
1) 365 – 6x = 6561
3
2) (4 √2 ) 6x - 12 = 128
3) 0,80,8 – 5x =0,5 √5
4) 4
𝑥+3
𝑥
+4
2𝑥+3
𝑥
= 320
5) 36x - 13 · 6x + 36 = 0 (Если уравнение имеет несколько корней, в ответе укажите
сумму всех его корней.)
Вариант №10*.
1) 110,3 – 3x = 1331
6
2) ( 81 √3 )12x – 9 = 729
3) 2,25x – 4 = 0,5 √6
4) 5
3𝑥+9
𝑥
− 5
𝑥+9
𝑥
= 0,96
5) 104x – 133 · 100x + 1000 = 0 (Если уравнение имеет несколько корней, в ответе
укажите сумму всех его корней.)
Ответы к работе №6.
Показательные уравнения.
№ задания
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
1
-0,6
4
-5,5
1,5
0,25
0,5
-3
6
9,5
-0,9
2
-4
-2,5
-1,5
-0,625
1,2
1,25
-1
3
2,5
0,87
3
0,06
-0,7
-2,5
-7,75
-1,9
0,75
9,75
0,125
0,26
4,75
4
2
3
-2
-5
-3,5
-1,2
-0,6
-0,5
1,5
-3
5
0
1
0
-2
0,75
3
0,5
1
2
1,5
Работа № 7.
Логарифмические уравнения.
Вариант № 1.
1) log6 (5x – 4 ) = 3
2) log3 (x2 – 6x) = log3 (6x – 27 )
3) log2 (12x - 13 ) = 3 log2 11
4) log2x+2 25 = 2
5) log 22 (32𝑥 ) − 11 log 2 𝑥 = 17 (Если уравнение имеет более одного корня, в
ответе укажите произведение всех корней уравнения)
Вариант 2.
1. lg(3x − 2) = 3
2. log 8 (x 2 − 3x) = log 8 (5x − 12)
3. log 9 (11x − 12) = 3 log 9 10
4. log 3−2x 64 = 2
5. log 20,25 (64𝑥) + 8 log 0,25 𝑥 = 17 (Если уравнение имеет более одного корня, в ответе
укажите произведение всех корней уравнения.)
Вариант 3.
1. log 8 (3𝑥 + 8) = 3
2. log 7 (6x − x 2 ) = log 7 (33 − 8x)
3. log 6 (5x + 4) = 4 log 6 5
4. log 3−2x 1,96 = 2
5. lg 2 (1000𝑥) − 10 log100 𝑥 = 21 (Если уравнение имеет более одного корня, в ответе
укажите произведение всех корней уравнения.)
Вариант 4.
1. log1,1 (0,01𝑥 + 0,001) = 3
2. log 2,2 (32𝑥 − 𝑥 2 ) = log 2,2 (42 − 11𝑥)
3. log 3,3 (4𝑥 + 5) = 5 log 3,3 4
4. log 4−4𝑥 3,61 = 2
5. log 20,2 (625𝑥) + 14 log 0,04 𝑥 = 22 (Если уравнение имеет более одного корня, в
ответе укажите произведение всех корней уравнения.)
Вариант 5.
1. log 0,2 (5 − 4𝑥) = −3
2. log11 (7 − 5𝑥) = log11 (3 + 𝑥) + 1
3. log 25 (𝑥 + 5) = log 0,2 2
4. log 4𝑥−18 81 = 4
5. log 22 (64x) − 126 log 64 x = 24 (Если уравнение имеет более одного корня, в ответе
укажите произведение всех корней уравнения.)
Вариант 6.
1. log 0,25 (6𝑥 − 5) = −2
2. log12 (12 − 24𝑥) = log12 (36 − 48𝑥) − 1
3. lg(x − 0,09) + log 0,01 9 = 0
4. log 𝑥−5 64 = 6
5. log 23 (243x) − 80 log 243 x = 43 (Если уравнение имеет более одного корня, в ответе
укажите произведение всех корней уравнения.)
Вариант 7.
1.
log 0,25
25𝑥−2
6
= −2
𝑥
3
𝑥
5
7
5
3
7
2. log 2 ( + ) = log 2 ( + ) − 1
3. log 25 (0,5𝑥 + 0,375) = log 0,2 8 + 1
4. log 6𝑥−13 512 = 3
5. lg 2 (100𝑥 ) − 14 log100 𝑥 = 77 (Если уравнение имеет более одного корня,
в ответе укажите произведение всех корней уравнения.)
Вариант 8.
1. log 0,2
4𝑥+8
7
= −2
𝑥
1
1
𝑥
4
3
4
3
2. log 0,5 ( + ) = log 0,5 ( − ) + 1
3. log 4 (𝑥 + 2) = 2 log 0,25 5 − 1
4. log 𝑥−24 1024 = 10
5. log 20,1 (10x) − 2 log 0,01 x = 88 (Если уравнение имеет более одного корня,
в ответе укажите произведение всех корней уравнения.)
Вариант 9.
1. log 0,001 (111 − 11𝑥 ) = −
4
3
2. log 9 (27 − 54𝑥 ) = log 9 (81 − 108𝑥 ) − 1,5
3. log 2,25 (2𝑥 + 3) = log 2 5
3
4. log 3𝑥+2 0,4096 = 4
5. log 3 (𝑥 2 + 6𝑥 − 55) − log 9 (𝑥 2 + 22𝑥 + 121) = 99 (Если уравнение имеет
более одного корня, в ответе укажите произведение всех корней
уравнения.)
Вариант 10.
1. log 0,027
11−12𝑥
6
=−
1
3
2. log100 (15 − 60𝑥 ) = log100 (0,01 − 0,1𝑥 ) + 1,5
3. log 0,64 (3𝑥 − 50) = log1,25 0,5
4. log 5𝑥−6 0,0256 = 4
5. log 2 (𝑥 2 + 8𝑥 − 48) − log 4 (𝑥 2 + 24𝑥 + 144) = 55 (Если уравнение имеет
более одного корня, в ответе укажите произведение всех корней
уравнения.)
Решения уравнений.
𝐥𝐨𝐠 𝟐𝟐 (32x) – 78 𝐥𝐨𝐠 𝟖 𝒙 = 22 (Если уравнение имеет более одного корня, в
ответе укажите произведение всех корней уравнения.)
Решение. Так как log 2 (32𝑥) = log 2 (25 · 𝑥) = 5 + log2𝑥 и log8 x = log 23 𝑥 =
1
= log2 x, то данное в условии уравнение преобразуется к виду:
3
(5 + log2 x )2 – 26 log2 x = 22. Введём новое неизвестное t = log2 x.
Относительно неизвестного t уравнение имеет вид: (t + 5)2 – 26t = 22,
t2 – 16t + 3 = 0. Данное уравнение имеет два различных корня t1 и t2 .
Возвращаясь к неизвестному x, получаем, что исходное уравнение
равносильно совокупности уравнений log2 x = t1 и log2 x = t2 .
Следовательно, корнями исходного уравнения являются числа x1 · x2 = 2𝑡1 +𝑡2 . Осталось заметить, что по теореме Виета 𝑡1 + 𝑡2 = 16,
поэтому x1 · x2 = 216 = 210 · 26 = 1024 · 64 = 65536.
Ответ: 65536.
log3 (x2 + 10x – 144) – log9 (x2 + 36x + 324) = 14 (Если уравнение имеет
более одного корня, в ответе укажите сумму всех корней уравнения.)
Решение. Заметим, что x2 + 10ч – 144 = (x + 18) · (x – 8), а x2 + 36x + 324 =
=(x + 18)2. Поэтому log9 (x2 + 36x + 324) = log 32 (𝑥 + 18)2 = log3 │x+ 18│и
данное в условии уравнение преобразуется к виду:
log3 ((x + 18) · (x – 8)) – log3│x+ 18│ = 14,
log3
(x + 18) · (x – 8)
│x+ 18│
Если x > -18 , то
= 14,
(x + 18)
│x+ 18│
(x + 18) · (x – 8)
│x+ 18│
= 314
= 1 и уравнение упрощается к виду x – 8 = 314,
откуда x = 8 + 314.
Если же x < -18, то
x + 18
= - 1, уравнение упрощается к виду x – 8 = - 314,
│x+ 18│
откуда x = 8 - 314. Так как для чисел x1 > 18 и x2 < –18, то они действительно
являются корнями исходного уравнения, а их сумма равна 8 + 314 + 8 – 314
= 16.
Ответ:16.
Ответы к работе №7.
Логарифмические уравнения.
№ задания
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
1
44
334
168
133
-30
3,5
3,92
41,75
-899
-0,75
2
9
6
3
1
-1,625
0,45
10,2
-0,5
0,48
-0,125
3
112
92
124,2
254,75
-4,75
3,09
0,03125
-1,99
-1,48
18
4
1,5
-2,5
0,8
0,525
5,25
7
3,5
26
-0,4
1,28
5
2
16
0,1
0,2
512
729
1000
0,001
10
8
Решение тригонометрических уравнений.
cos 7x + cos 8x + cos 9x = 0 ( В ответе запишите величину наименьшего
положительного корня уравнения, выраженную в градусах.)
Решение
Так как cos 7x + cos 9x = 2 cos
7𝑥+9𝑥
2
· cos
9𝑥−7𝑥
2
= 2 cos 8x · cos x, то данное
в условии уравнение преобразуется к виду:
2 cos 8x · cos x + cos 8x = 0, cos 8x · (2 cos x + 1) = 0 и, значит, оно
равносильно совокупности уравнений cos 8x = 0 и 2cos x = – 1. Корнями
𝜋
уравнения cos 8x = 0 являются те x, для которых 8x = + πn, или
2
x=
𝜋
16
+
𝜋𝑛
8
, где nЄZ ⇒ наименьшим положительным корнем этого
уравнения является x =
𝜋
16
, что в градусах составляет
Корнями уравнения cos x = -0,5 являются x = ±
2𝜋
3
180о
16
= 11,250
+ 2πn, где nЄZ ⇒
наименьшим положительным корнем этого уравнения является x =
что в градусах составляет 1200.
Ответ 1200.
2𝜋
3
Самостоятельная работа №8.
Тригонометрические уравнения.
Число верных ответов
Оценка
0-1
2
2
3
3
4
Вариант 1.
1. cos
π(x−49)
= 0,5
21
В ответе запишите наименьший положительный корень уравнения.
2. 1 + 4sin2
π(x−3)
24
+ 8cos
π(x−3)
24
=0
В ответе запишите наибольший отрицательный корень уравнения.
3. cos 0,5𝑥 + cos 0,25𝑥 = 0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. 2 sin2 𝑥 − (2 + √2) sin 𝑥 cos 𝑥 + √2 𝑐𝑜𝑠 2 𝑥 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
Вариант 2.
1. cos
𝜋(𝑥+15)
18
=−
√3
2
В ответе запишите наименьший положительный корень уравнения.
2. 1 + 2 sin2
𝜋𝑥
18
+ √3 𝑐𝑜𝑠
𝜋𝑥
18
=0
В ответе запишите наибольший отрицательный корень уравнения.
3. cos 13𝑥 + cos 11𝑥 = 0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. 2 sin2 𝑥 + (3 + 2√3) sin 𝑥 cos 𝑥 + 3√3 cos2 𝑥 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
4
5
Вариант 3.
1. cos
π(x+18)
24
=
√2
2
В ответе запишите наименьший положительный корень уравнения.
2. 2 ∙ (1 + cos 2
𝜋𝑥
20
) − 3√2 sin
𝜋𝑥
20
=0
В ответе запишите наибольший отрицательный корень уравнения.
3. cos 3,5𝑥 + cos 1,5𝑥 = 0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. 2 sin2 𝑥 + 5 sin 𝑥 cos 𝑥 + 3 𝑐𝑜𝑠 2 𝑥 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
Вариант 4.
1. cos
𝜋(𝑥+20)
30
= −0,5
В ответе запишите наименьший положительный корень уравнения.
2. 4 sin2
𝜋𝑥
21
+ 4 𝑐𝑜𝑠
𝜋𝑥
21
=1
В ответе запишите наибольший отрицательный корень уравнения.
x
x
2
2
3. cos − cos
=0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. 2√3 sin2 𝑥 + (3√3 + 2) sin 𝑥 cos 𝑥 + 3 cos2 𝑥 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
Вариант 5.
1. sin
π(x+9)
12
=
√3
2
В ответе запишите наименьший положительный корень уравнения.
𝜋𝑥
𝜋𝑥
2. √2 cos 2 + sin = 0
10
10
В ответе запишите наибольший отрицательный корень уравнения.
3. sin 12x + sin 13x = 0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. 3 sin2 𝑥 + 4 sin 𝑥 cos 𝑥 − 3 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
Вариант 6.
1. sin
𝜋(𝑥+21)
15
=−
√3
2
В ответе запишите наименьший положительный корень уравнения.
2. 4 sin2
2𝜋𝑥
3
+ 5√2 𝑐𝑜𝑠
2𝜋𝑥
3
=7
В ответе запишите наибольший отрицательный корень уравнения.
3. sin 0,1𝑥 + sin 0,9𝑥 = 0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. 1 − √3 sin 𝑥 cos 𝑥 − cos2 𝑥 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
Вариант 7.
1. sin
π(x+28)
16
=−
√2
2
В ответе запишите наименьший положительный корень уравнения.
2. 6 cos 2
𝜋𝑥
+ √3sin
9
𝜋𝑥
9
=0
В ответе запишите наибольший отрицательный корень уравнения.
3. sin
x
2
+ sin 2x = 0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. 2 𝑐𝑜𝑠2 x + 6√3 sin x cos x +3 =0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
Вариант 8.
1. sin
𝜋(𝑥+11)
6
= −0,5
В ответе запишите наименьший положительный корень уравнения.
2. 8 sin2
2𝜋𝑥
9
+ 2(√3 + 2) 𝑐𝑜𝑠
2𝜋𝑥
9
= 8 + √3
В ответе запишите наибольший отрицательный корень уравнения.
3. sin 6𝑥 + sin 12𝑥 = 0
В ответе запишите величину наименьшего положительного корня уравнения,
выраженную в градусах.
4. (2 − √7) sin2 x + (2 + √7)sin 𝑥 cos 𝑥 + √7 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
Вариант 9*
1. cos
π(x−78)
36
=
√3
2
В ответе запишите наибольший отрицательный корень.
2. 6 cos 2
𝜋𝑥
9
+ 7sin
𝜋𝑥
9
=8
В ответе запишите наименьший положительный корень.
3. sin 3𝑥 + sin 5x + sin 8x = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
4. sin2 2 𝑥 + cos 2 5𝑥 = 1
В ответе укажите число решений этого уравнения, принадлежащих промежутку
(0; 4π).
Вариант 10*
1. 𝑠𝑖𝑛
π(x−56)
32
=
√2
2
В ответе запишите наибольший отрицательный корень.
2. 12 sin2
𝜋𝑥
102
+ 8cos
𝜋𝑥
102
= 13
В ответе запишите наименьший положительный корень.
3. sin 5𝑥 + sin 8x + sin 13𝑥 = 0
В ответе запишите величину наибольшего отрицательного корня уравнения,
выраженную в градусах.
4. cos 2 20 𝑥 + cos 2 12𝑥 = 2
В ответе укажите число решений этого уравнения, принадлежащих промежутку
(0; 10π).
Ответы к работе №8. Тригонометрические уравнения.
№ задания
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
1
14
6
24
20
19
4
24
8
-60
-48
2
-13
-15
-25
-14
-2,5
-0,375
-3
-1,5
1,5
34
3
240
7,5
36
432
14,4
225
120
10
-36
-22,5
4
-135
-60
-45
-30
-90
-120
-30
-45
35
39
Самостоятельная работа №9.
Анализ и чтение графиков функций.
Рекомендуемое время для выполнения работы 25 минут.
Рекомендуемая шкала оценивания результатов
Число верных ответов
оценка
0-1
2
2
3
3
4
4
5
Вариант 1.
1. На рисунке показано изменение среднесуточной температуры в г. Барнаул в период
с 10 по 16 июня 1987г. По горизонтали указаны даты, по вертикали – температура в
градусах Цельсия. Определите по рисунку разность между максимальной и
минимальной среднесуточными температурами (в градусах Цельсия) в период с 12 по
15 июня.
t, ˚C
25
24
23
21
10
11
12
13
14
15
16
2. Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая
на крылья, зависит только от скорости. На графике изображена эта зависимость для
некоторого самолёта. На оси абсцисс откладывается скорость, измеряемая в км/ч, на
оси ординат – сила, измеряемая в тоннах силы (тс). Определите минимально
возможное значение скорости самолёта (в км/ч) при горизонтальном полёте, если
требуется, чтобы подъёмная сила была меньше, чем 45 тс.
F, mc
15
0
40
V, км/ч
3. Автомобильный завод выпустил в продажу две новые модели машин – модель A и
модель B. На графиках показано, как эти модели продавались в течение года. (По
горизонтальной оси откладывается время, прошедшее с начала продаж, в месяцах;
по вертикальной – число проданных за это время машин в тыс. шт.) Сколько всего
машин этих двух моделей (в тыс. шт.) было продано за первые семь месяцев?
Число машин
,
тыс. шт.
240
Модель B
180
120
Модель A
60
2
6
4
10
8
месяцы
12
4. На рисунке показано изменение биржевой стоимости акций горнодобывающей
компании во второй половине сентября. 16 сентября бизнесмен приобрёл 600 акций
этой компании. 500 акций он продал 23 сентября, а остальные акции продал 26
сентября. Сколько рублей приобрёл бизнесмен в результате этих операций?
руб.
180
160
140
14
16
18
20
22
24
26
28
5.Грузовая машина отправилась из магазина на склад, где провела некоторое
время в процессе погрузки, и вернулась обратно по тому же самому
маршруту. На рисунке изображён график движения этой машины: по оси
абсцисс откладывается время (в минутах) с момента выезда машины от
магазина, по оси ординат – расстояние от машины до магазина (в км, в0доль
маршрута движения). Определите по графику, сколько километров проехала
машина
за 2часа 15 минут с момента выезда.
S, км.
45
30
15
мин.
30
60
90
120
150
t
Ответы к работе №9
Анализ и чтение графиков функций.
№ задания
Вариант 1
Вариант 2
1
2
3
2
200
45
3
300
18
4
20000
8500
Самостоятельная работа№10.
Рекомендуемое время для выполнения работы 40 минут.
Шкала оценивания результатов
Число верных
ответов
оценка
0-1
2
3-4
5
2
3
4
5
Вариант 1
1. Функция y=f(x) определена на промежутке (-4;3). На рисунке изображён её график и
касательная к этому графику в точке с абсциссой 𝑥0 = 2 . Вычислите значение
производной f ’(x) в точке 𝑥0 = 2.
2. Прямая y=3x+4 параллельна прямой l , которая является касательной к графику
функции y = 𝑥 2 -2x. Найдите ординату точки касания прямой l и данного графика.
3. Функция y= f(x) определена на промежутке (-5;5). На рисунке изображён график её
производной. Укажите точку максимума функции y = f(x) на промежутке (-5;5).
4. При движении тела по прямой расстояние S (в метрах) до точки отсчёта изменялось
по закону: S(t) = 5𝑡 2 + 5 = 6𝑡, где t – время в секундах, прошедшее от начала
движения. Вычислите скорость тела (в м/с) через 7 секунд после начала движения.
5. Найдите наибольшее значение функции y = -𝑥 3 + 3𝑥 − 33 на отрезке [-3;3].
Производная. Исследование функций с помощью производной
(взаимосвязь между свойствами функции и её производной).
Два основных типа заданий: 1) задачи на геометрический смысл производной;
2) задачи на исследование промежутков монотонности и точек экстремумов
функции.
Для определения углового коэффициента k прямой y = k x+b по её изображению на
𝑦 𝑦
координатной плоскости. При этом используется следующая формула: k= 1 2 ; где
𝑥1 𝑥2
(𝑥1 ; 𝑦1 ), ( 𝑥2 ; 𝑦2 ) - координаты каких-либо точек А и В, принадлежащих прямой
y = kx+b.
Функция y = f(x) определена на промежутке (-4;5). На рисунке изображён её график и
касательная к этому графику в точке с абсциссой 𝑥0 =1. Вычислите значение
производной f ’(x) в точке 𝑥0 =1.
Решение.
По рисунку определяем, что касательная к данному графику y = f(x) в точке с
абсциссой 𝑥0 =1 проходит через точки с координатами (1; -2) и (5; -1). Находим
угловой коэффициент k к этой касательной по указанной выше формуле k=
−2−(1)
1−5
=
Заменяя понятие «угловой коэффициент касательной» на значение производной в
точке, получаем ответ.
Ответ: 0,25.
1
4
На рисунке изображён график функции y = f(x). Прямая, проходящая через точку(3;1), касается этого графика в точке с абсциссой 𝑥0 =2. Найдите значение производной
f ’(2).
Решение.
Проведём касательную, о которой идёт речь в условии, соединив прямой линией точку
(-3;1) и точку графика с абсциссой 𝑥0 =2, см. рисунок выше. Так как эта касательная
проходит через точки (-3;1) и (2;3), то её угловой коэффициент равен
3−1
2−(−3)
= 0,4.
Поэтому f ’(2)=0,4.
Ответ: 0,4.
Среди заданий на геометрический смысл производной есть и такие, в условии
которых не приведён какой-либо рисунок.
Рассмотрим следующие примеры.
Прямая y=5x-1 параллельна прямой l, которая является касательной к графику
функции 𝑦 = 𝑥 2 − 4𝑥 − 5. Найдите абсциссу точки касания прямой l данного графика.
Решение.
Так как прямая l параллельна прямой y = 5x – 1, то её угловой коэффициент равен 5.
Пусть прямая l касается графика y = x2 – 4x – 5 в точке x0 . Тогда её угловой
коэффициент равен значению производимой функции y = x2 – 4x – 5 в точке x0 , т.е.
равен y/ (x0) – 2x0 – 4 . Следовательно , 2x0 – 4 = 5, x0 = 4,5.
Ответ: 4,5.
Прямая y = 80x + 76 является касательной к графику функции y= x3 – 3x2 + 8x – 100.
Найдите ординату точки касания.
Решение.
Пусть x0 – абсцисса точки касания данных прямой и графика. Тогда угловой
коэффициент прямой y = 80x + 76 равен значению производной функции
y = x3 – 3x2 + 8x – 100 в точке x0 , т.е. равен 3𝑥02 – 6x0 + 8.
Отсюда имеем уравнение: 80 = 3𝑥02 – 6x0 + 8, корнями которого являются числа 6 и –4.
В точке касания также должно быть выполнено следующее условие: 80x + 76 = x3 –
3x2 + 8x – 100, (точка касания принадлежит и прямой y = 80x + 76 и заданному
графику ). Подставляя в это равенство поочерёдно x =6 , x = – 4 , получаем , что в
точке x = 6 равенство не выполнено , а в точке x = – 4 оно выполнено, при этом
значения левой и правой части равны – 244. Следовательно, абсцисса точки касания
равна – 4, а искомая ордината точки касания равна – 244.
Ответ: – 244.
Прямая y = k ∙ x + 56 является касательной к графику функции y = x3 + 4x + 110.
Найдите значение коэффициента k.
Решение.
Пусть x0 – абсцисса точки касания данных прямой и графика . Тогда угловой
коэффициент прямой y = k · x + 56 равен значению производной функции y = x3 + 4x +
110 в точке x0 и, значит , k = 3𝑥02 + 4. Отсюда , учитывая так же то , что точка касания
принадлежит одновременно и прямой y = k · x + 56 и заданному графику , получаем
уравнение : (3𝑥02 + 4) · x0 + 56 = 𝑥03 + 4x0 + 110. Решая это уравнение , находим : 3𝑥02 =
54 , 𝑥03 = 27, k = 3𝑥02 + 4 = 31.
Ответ: 31.
Прямая y = 7x +28 является касательной к графику функций
y = ax2 – 21x +3a.Найдите значение коэффициента а, если известно, что абсцисса точки
касания положительна .
Решение.
Пусть х0 – абсцисса точки касания данных прямой и графика. Тогда угловой
коэффициент прямой у = 7х + 28 равен значению производной функции у = ах2 – 21х
+ 3а в точке х0. Отсюда имеем : 7 =2ах0 – 21 , ах0 = 14. Учитывая, что точка касания
принадлежит одновременно и прямой у = 7х + 28 и заданному графику, получаем
второе уравнение: 7х0 + 28 = ах20 – 21х0 + 3а, или 28х0 +28 = ах20 + 3а. Подставив в это
уравнение aх0 =14, получим:28х0 + 28 = 14х0 + 3а, 14х0 + 28 =3а.
Итак, для неизвестных х0 , а имеем следующую систему уравнений :
𝑎=
14
𝑎=
14
х0
𝑎х = 14
х0
⇔{
⇔ {х2 + 2х − 3
{ 0
14
14х0 = 3а
0
0
14х0 + 28 = 3 ·
=0
х0
х0
Корнями второго уравнения последней системы являются х0 = 1 и х0 = - 3.
По условию абсцисса точки касания положительна , поэтому х0 = 1, а = 14.
Обсуждение заданий
на геометрический
рассмотрением группы авторских примеров:
смысл
производной
завершим
На рисунке изображена прямая l , которая является касательной к графику функций у
= х3 + bx + c в точке с абсциссой х0 = - 1.
Найдите значение коэффициента с.
у
Решение.
По рисунку находим , что прямой l
принадлежат точки с координатами (-1;1) и
l
1
(1;0). Значит .угловой коэффициент прямой l
равен
0−1
1−(−1)
0
1
х
= - 0,5. Так как эта прямая касается
графика у = х3 + bx + c в точке с координатами
(-1;1), то справедливы следующие равенства: (-1)3 +b · (- 1) + с = 1 – условие того , что
точка (-1;1) принадлежит графику ; 3 · (-1)2 + b = - 0,5 условие того , что значение
производной (х3 +bx + c) / = 3х2 + b в точке с абссцисой - 1 равно угловому
коэффициенту касательной l . т.е. равно - 0, 5. Таким образом имеем:
3 + 𝑏 = −0,5
𝑏 = −3,5
𝑏 = −3,5
⇔{
⇔{
{
𝑐 = −1,5.
𝑐 =𝑏+2
− 1 –𝑏 + 𝑐 = 1
Ответ: -1,5.
На рисунке изображены участок графика
функции у = хn и касательная к этому
графику в точке с абсциссой х = 1.
Используя данный рисунок , определите ,
чему ровно n.
Решение.
Касательная к графику y = xn в точке с
абсциссой
х = 1, изображённая на рисунке , содержит точки с координатами (1;1) и (2;5).
Поэтому угловой коэффициент этой касательной равен
5−1
2−1
= 4.
С другой стороны , угловой коэффициент касательной равен значению производной
(хn)′ = n · xn-1 в точке х = 1, т.е. равен n. Следовательно , n = 4.
Ответ: 4.
На рисунке изображены участки графика функции у = f ′ (x) и касательной к нему в
точке с абсциссой х = 0. Известно , что данная касательная параллельна прямой ,
проходящей через точки графика с абсциссами х = - 2 и х = 3. Найдите значение
производной f ′ (0).
Решение.
у
0
х
1
Так как значение производной f ′ (0) равно угловому коэффициенту касательной к
графику у = f (х) в точке с абсциссой х = 0, то достаточно найти угловой коэффициент
этой касательной . По условию, эта касательная параллельна прямой , проведённой
нами на рисунке пунктиром . Следовательно , её угловой коэффициент равен
= 0,2.
Ответ: 0,2.
2−1
3−(−2)
=
Самостоятельная работа № 10 .
Вариант № 1.
у
y = f(x)
1
1) Функция у = f (x) определена на промежутке
(- 4;3). На рисунке изображён её график и
касательная к этому графику в точке с абсциссой
х0 = 2. Вычислите значение производной f ′ (x)
в точке х0 = 2.
0
1
х
2) Прямая у = 3х + 4папраллельноя прямой l , которая является касательной к графику
функций у = х2 – 2х. Найдите ординату точки касания прямой l и данного графика.
3) Функция у = f (x) определена на промежутке (-5;5). На рисунке изображён график
её производной. Укажите точку максимума функции у = f (х) на промежутке (-5;5).
у
1
y = f (x)
0
1
х
4) При движении тела по прямой расстояние S (в метрах) до точки отсчёта
изменялось по закону : S(t) = 5t2 + 6t , где t – время в секундах, прошедшее от начала
движения . Вычислите скорость тела (в м/с) через 7 секунд после начала движения.
5) Найдите наибольшее значение функции y = - x3 + 3x – 33 на отрезке [-3;3].
Вариант №2.
1) Функция у = f (x) определена на промежутке (-4;5). На рисунке изображён график
её производной. Найдите количество точек, в которых
угловой коэффициент касательной к графику
y = f′(x)
функции у = f (x) является целым числом.
1
2) Прямая у = 9х + 7 является касательной к графику
0
1
функций у = 5х2 – 3х + с. Найдите значение
коэффициента с.
3) На рисунке изображён график функции у = f (x), определённой на промежутке (-5;5)
Найдите количество точек целыми абсциссами, в которых производная этой функции
отрицательна.
у
1
0
1
х
4) Найдите точку максимума функции у = (4х - 3) cos x – 4 sin x, принадлежащую
промежутку (0;2π).
5)Найдите наименьшее целое значение функции у = 3х4 – 10х3 + 30.